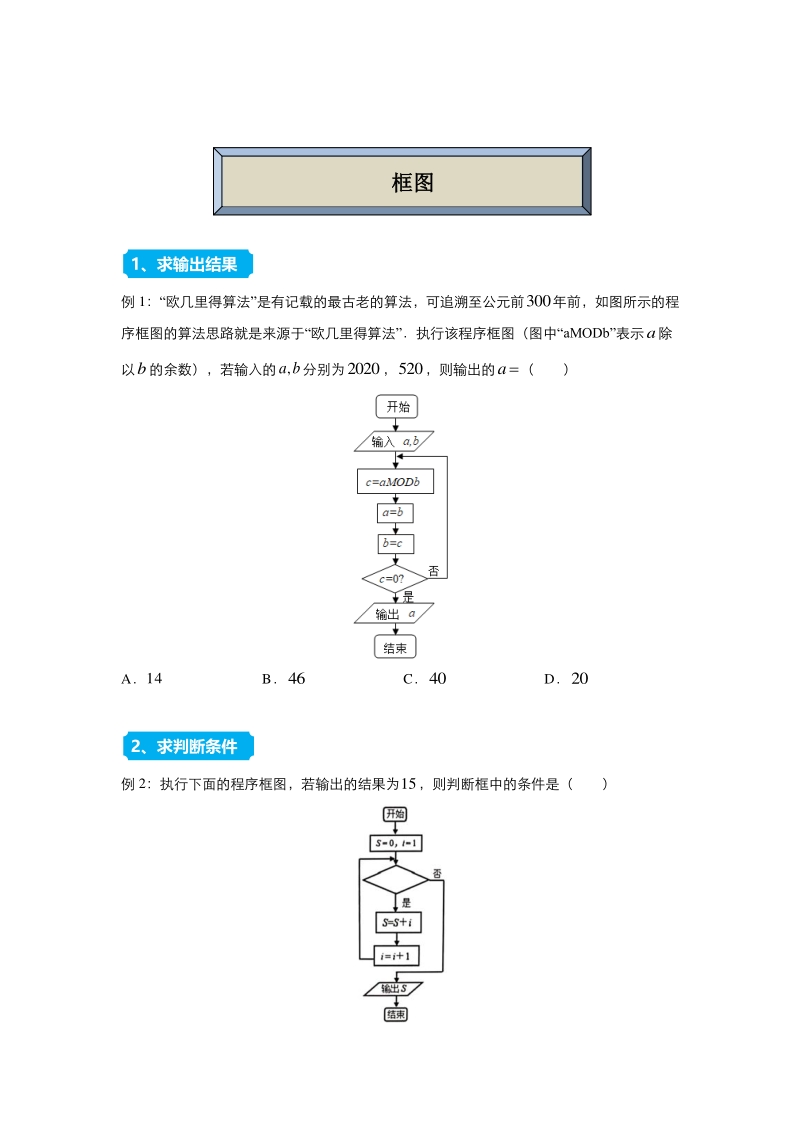
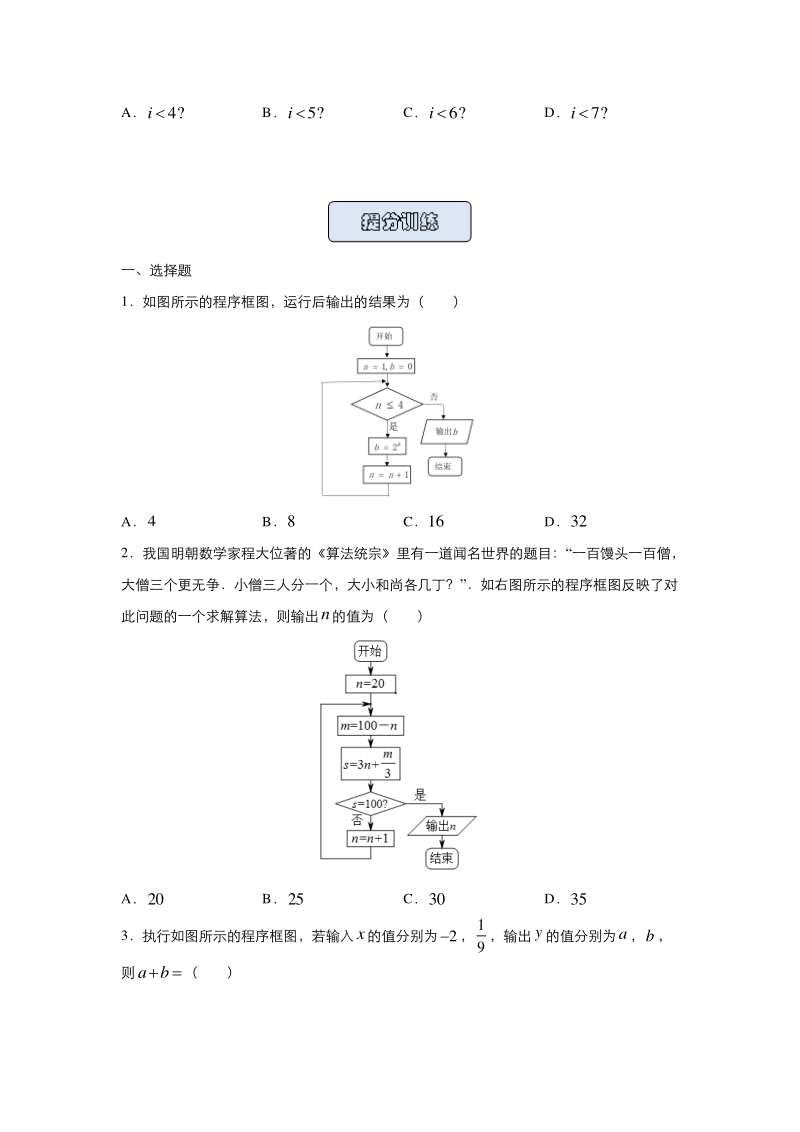
1、 例 1：“欧几里得算法”是有记载的最古老的算法，可追溯至公元前300年前，如图所示的程 序框图的算法思路就是来源于“欧几里得算法”执行该程序框图（图中“aMODb”表示a除 以b的余数），若输入的, a b分别为2020，520，则输出的a（ ） A14 B46 C40 D20 例 2：执行下面的程序框图，若输出的结果为15，则判断框中的条件是（ ） 1、求输出结果 2、求判断条件 框图框图 A4?i B5?i C6?i D7?i 一、选择题 1如图所示的程序框图，运行后输出的结果为（ ） A4 B8 C16 D32 2我国明朝数学家程大位著的算法统宗里有一道闻名世界的题目：“一百馒头一百僧
2、， 大僧三个更无争小僧三人分一个，大小和尚各几丁？”如右图所示的程序框图反映了对 此问题的一个求解算法，则输出n的值为（ ） A20 B25 C30 D35 3执行如图所示的程序框图，若输入x的值分别为2， 1 9 ，输出y的值分别为a，b， 则ab（ ） A4 B2 C 7 4 D 1 4 4宋元时期数学名著算学启蒙中有关于“松竹并生”的问题：松长五尺，竹长两尺，松 日自半，竹日自倍，松竹何日而长等，如图是源于其思想的一个程序框图，若输入的a，b 分别为5,2，则输出的n等于（ ） A2 B3 C4 D5 5执行如图所示的程序框图，则输出的S （ ） A 1 4 B 3 10 C 1 3 D
3、 5 14 6阅读右侧的算法框图，输出结果S的值为（ ） A1 B3 C 1 2 D 3 2 7如图（1）、（2），它们都表示的是输出所有立方小于 1000 的正整数的程序框图，那么 应分别补充的条件为（ ） A（1） 3 1000n ？（2） 3 1000n ？ B（1） 3 1000n ？（2） 3 1000n ？ C（1） 3 1000n ？（2） 3 1000n ？ D（1） 3 1000n ？（2） 3 1000n ？ 8右图是求 1210 ,x xx， ,的乘积 S 的程序框图，图中空白框中应填入的内容为（ ） A(1)SSn B 1m SSx CSS n D m SSx 9如图给
4、出的是计算 1111 24620 的值的一个框图，其中菱形判断框内应填入的条 件是（ ） A8i B9i C10i D11i 10一个算法的程序框图如图所示，若执行该程序输出的结果是1，则判断框内可填入的 条件是（ ） A6?i B7?i C7?i D6?i 二、填空题 11执行下边的程序框图，若14p ，则输出的n的值为_ 12下图是一个算法流程图，则输出的S的值是_ 例 1：【答案】C 【解析】2020a，520b，460c，N； 520a ，460b，60c ，N； 460a ，60b，40c ，N； 60a ，40b，20c ，N； 40a，20b，0c =，Y 输出40a，故选 C
5、例 2：【答案】C 【解析】当0S 时，不满足输出结果为15，进行循环后，1S ，2i ； 当1S 时，不满足输出结果为15，进行循环后，3S ，3i ； 当3S 时，不满足输出结果为15，进行循环后，6S ，4i ； 当6S 时，不满足输出结果为15，进行循环后，10S ，5i ； 当10S 时，不满足输出结果为15，进行循环后，15S ，6i ； 当15S 时，满足输出结果为15， 故进行循环的条件，应为6?i，故选 C 一、选择题 1【答案】C 【解析】执行如图程序框图：当1,2bn，当2,3bn，当4,4bn， 当16,5bn，当5n则输出b，故选 C 2【答案】B 【解析】输出20,
6、80,100nms； 21,79,100nms； 22,78,100nms； 23,77,100nms； 24,76,100nms； 25,75,100nms， 退出循环，输出25n，故选 B 3【答案】C 【解析】由程序框图可知：程序框图的功能是计算分段函数的函数值， 当2x时， 2 1 2 4 y ，所以 1 4 a ， 当 1 9 x 时， 3 1 log2 9 y ，所以2b， 所以 17 2 44 ab ，故选 C 4【答案】C 【解析】当1n 时， 15 2 a ，4b，满足进行循环的条件； 当2n时， 45 4 a ，8b，满足进行循环的条件； 当3n时， 135 8 a ，16
7、b ，满足进行循环的条件； 当4n时， 405 16 a ，32b，不满足进行循环的条件，故输出的n值为4，故选 C 5【答案】B 【解析】2k ， 1 6 S ，3k ， 2 111 6334 S ；4k ， 2 113 44410 S 6【答案】D 【解析】 220113 0sinsinsinsin 3333 2 s 7【答案】C 【解析】根据两个程序框图分析：（1）为当型循环结构， 故判断框内应为满足循环的条件 （2）为直到型循环结构，故判断框内为不再满足循环的条件 （1）内应填 3 1000n ？，（2）内应填 3 1000n ？，故选 C 8【答案】D 【解析】本题主要考查程序框图的
8、运用，重点是分析循环结构 由图知空白框处在一个循环体中，开始时1n ，1S 每循环一次n增加1， 由输出结果可知第K次循环后S应为循环前的 K x倍，故选 D 9【答案】C 【解析】由题意可知由 1 2 加到 1 20 需要进行10i ，即当11 10i 时运算就结束了， 故选 C 10【答案】D 【解析】1i 进入循环，2i ，1T ，20 1 19P ； 否，3i ，2T ，19217P； 否，4i ，3T ，17 3 14P ； 否，5i ，4T ，14 40P； 否，6i ，5T ，10 55P ； 否，7i ，6T ，5 61P ， 此时应满足判断条件，所以判断框内可填入的条件是6?
9、i ，故选 D 二、填空题 11【答案】4 【解析】模拟程序的运行，可得14,1,0pnS， 满足条件14S ，执行循环体，2,2Sn； 满足条件14S ，执行循环体，6,3Sn； 满足条件14S ，执行循环体，14,4Sn； 此时，不满足条件14S ，推出循环，输出n的值为4， 故答案为4 12【答案】1024 【解析】第一次循环，010k 成立， 0 12S ，0 1 1k ； 第二次循环，1 10k 成立， 01 122S ，1 12k ； 第三次循环，210k 成立， 012 1222S ，2 13k ； 以此类推，执行最后一次循环，910k 成立， 0129 12222S ， 9 1 10k ； 10 10k 不成立，输出 10 0129 1 2 1 222211024 1 2 S ， 故答案为1024
