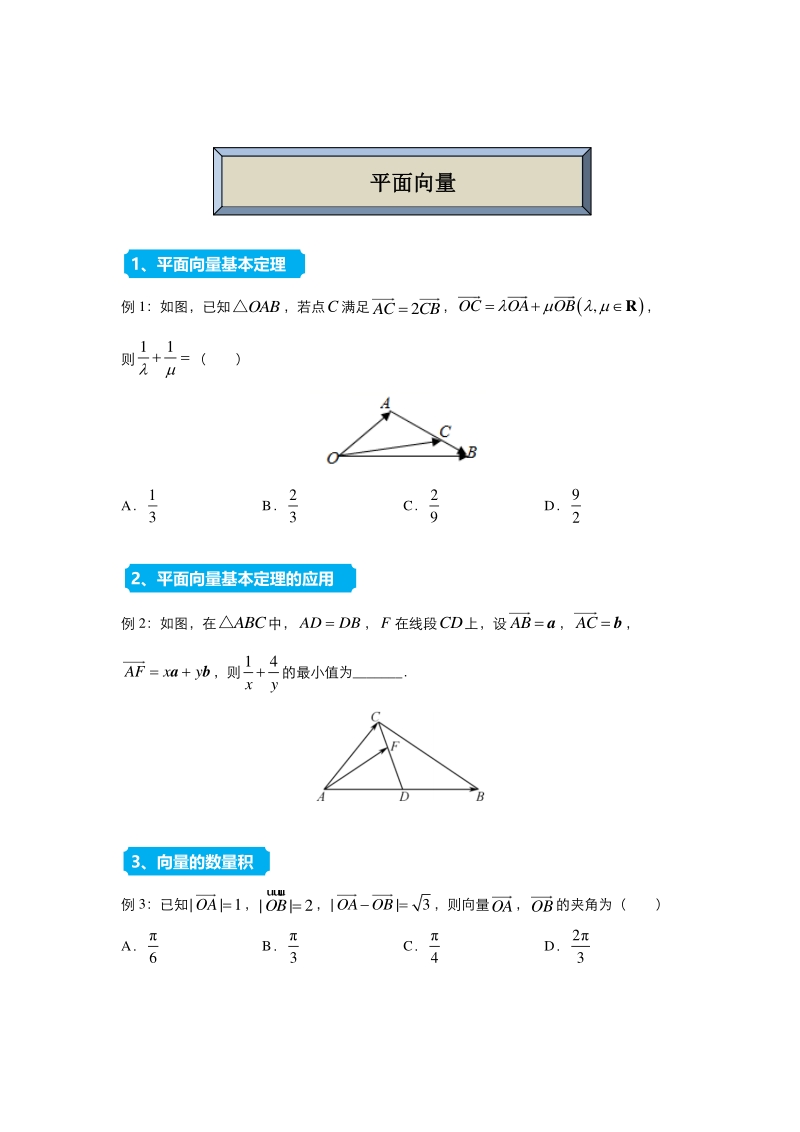
1、 例 1：如图，已知OAB，若点C满足 2ACCB ，,OCOAOB R， 则 11 （ ） A 1 3 B 2 3 C 2 9 D 9 2 例 2：如图，在ABC中，ADDB，F在线段CD上，设AB a，AC b， AFxyab，则 14 xy 的最小值为_ 例 3：已知| 1OA ，| | 2OB uu u r ，|3OAOB，则向量OA，OB的夹角为（ ） A 6 B 3 C 4 D 2 3 2、平面向量基本定理的应用 1、平面向量基本定理 3、向量的数量积 平面平面向量向量 例 4：已知点M是边长为 2 的正ABC内一点，且AMABAC，若 1 3 ， 则MB MC 的最小值为_ 一、
2、选择题 1设M是ABC所在平面上的一点， 33 22 MBMAMC 0，D是AC的中点， tMBDM ，则实数t的值为（ ） A 1 2 B 1 3 C2 D1 2已知菱形ABCD的边长为4，60ABC，E是BC的中点 2DFAF ， 则AE BF （ ） A24 B7 C10 D12 3在直角ABC中，点P是斜边AB上一点，2CACB，2BPPA则CP CA CP CB（ ） A4 B2 C2 D4 4 在正方形ABCD中，E为CD边上一点， 且60ABE， 9AB AC uu u r uuu r ， 则A B B E uuu r uur （ ） A3 3 B3 3 C 3 6 D3 6 5
3、三角形ABC所在平面内一点P满足PA PB PB PCPC PA ，那么点P是三角形 4、平面向量的应用 ABC的（ ） A重心 B垂心 C外心 D内心 6在矩形ABCD中，3AB，4AD ，点P是以点C为圆心，2为半径的圆上的动点， 设AP ABAD uu u ruu u ruuu r ，则的最小值为（ ） A1 B 7 6 C2 D 8 3 7在ABC中，2AB ，3AC ， 5 cos 6 A ，若O为 ABC的外心（即三角形外接 圆的圆心），且AO mABnAC ，则2nm（ ） A19 9 B 41 22 C 1 11 D17 11 8在ABC中，角, ,A B C的对边分别为 ,
4、,a b c已知 2 5c ，且2 sincosaCB 5 sinsinsin 2 aAbBbC ， 点 O 满足OA OB OC 0， 3 cos 8 CAO， 则ABC 的面积为（ ） A3 5 B 55 4 C 55 2 D 55 二、填空题 9 在ABC中，60BAC，4AB ，6AC ， 2ABAD ， 2AEEC ， 2EFFD ， 则BF DE 的值为_ 10如图，在ABC中，D为AB的中点， 2DEEC ，若BExAByAC， 则x y_ 11 如图， 在四边形ABCD中，1ABCD， 点,M N分别是边,AD BC的中点， 延长BA 和CD交NM的延长线于不同 的两点,P Q
5、，则()PQABDC的值为_ 12如图，在ABC中， 3 2 ACBC，点M，N分别在AC，BC上，且 1 3 AMAC， 1 2 BNBC若BM与AN相交于点P，则 CP AB 的取值范围是_ 13已知A、B、C是半径为5的圆M上的点，若 6BC ，则AB AC uu u r uuu r 的取值范围是 _ 14已知平面上四个互异的点A、B、C、D满足： 20ABACADBDCD， 则ABC的形状是 15已知点O为三角形ABC所在平面内的一点，且满足 1OAOBOC，3OA 45OBOC0，则AB AC_ 16如图，在ABC中，已知2AB ，4AC ，60A若D为BC边上的任意一 点，M为线段
6、AD的中点，则()MBMCAD的最大值是_ 例 1：【答案】D 【解析】因为 2ACCB ，所以2OCOAOBOC， 整理得到 12 33 OCOAOB，所以 1 3 ， 2 3 ， 119 2 ，故选 D 例 2：【答案】6 4 2 【解析】2AFxyxAByACxADyACab， 由图可知 xy， 均为正数，又,C F D三点共线，则21xy， 则 14148 22464 2 yx xy xyxyxy 例 3：【答案】B 【解析】设向量OA，OB的夹角为， 由题可知|3OAOB，两边平方可得 22 23OAOOBAOB， 又| 1OA ，| 2OB uu u r ，所以1OA OB，所以
7、1 cos 2 OA OA OB OB ， 又0,，所以 3 ，故选 B 例 4：【答案】 1 3 【解析】取BC的中点O，以点O为坐标原点， OC、OA所在直线分别为x、y轴建立平面直角坐标系xOy， 则点0, 3A、1,0B 、1,0C， 设点,M x y， ,3AMx y， 1,3AB ， 1,3AC ， AMABAC且 1 3 ，则33 1 3 x y ，可得 1 2 3 2 3 3 x y ， 由于点M在正ABC内，则 0 0 ，可得 1 0 3 ，则 1 1 , 3 3 x ， 2 3 1, 3 MBx ， 2 3 1, 3 MCx ， 22 41 1 33 MB MCxx ， 所
8、以，当0 x时，MB MC 取最小值 1 3 ，故答案为 1 3 一、选择题 1【答案】B 【解析】因为D是AC的中点，所以 2MA MCMD ， 又因为 33 22 MBMAMC 0，所以 11 + 1 323 MBMAMCMB MD 0（）， 所以 1 3 MBDM， 因为tMB DM ，所以 1 3 t ，故选 B 2【答案】D 【解析】由已知得 1 3 AFAD， 1 2 BEBC，AD BC ， 所以 11 22 AEABBCABAD， 1 3 BFAFABADAB 因为在菱形ABCD中，60ABC，所以120BAD 又因为菱形ABCD的边长为4， 所以 1 | |cos120448
9、 2 AB ADABAD ， 所以 22 1111 | 2366 AE BFABADABADABAB ADAD 11 16( 8)1612 66 ， 故选 D 3【答案】D 【解析】由2BPPA，知 12 33 CPCBCA， 221212 4 3333 CP CACP CBCBCACACBCBCA ，故选 D 4【答案】A 【解析】因为 2 22 |2 |9 22 AB ACAB ACABABAB ， 所以3AB 因为60ABE，所以30CBE，所以2 3BE ， 故 3 2 3 cos1203 3AB BE ，故选 A 5【答案】B 【解析】由于三角形ABC所在平面内一点 P 满足PA P
10、B PB PCPC PA ， 则0PAPBPC，0PBPAPC，0PCPBPA， 即有 0PA CB ， 0PB CA ， 0PC AB ， 即有PA CB ，PB CA ，PC AB ， 则点 P 为三角形ABC的垂心，故选 B 6【答案】B 【解析】如图，建立平面直角坐标系，故可得3,4C，0,0 ,3,0 ,0,4ABD， 故点 P 在圆 22 :344Cxy上， 设2cos3,2sin4P，3,0AB ，0,4AD ， 又AP ABAD uu u ruu u ruuu r ，所以 2cos33 2sin44 ， 从而 2157 cossin2sin2 3266 ，故选 B 7【答案】D
11、 【解析】设,D E分别为,AB AC的中点，连接,OD OE， 则ODAB，OEAC， 又OD ADAO ，即 11 2 22 m ODABmABnACABnAC ， 同理 1 2 2 n OEAEAOACmAB ， 因为 2 1 2 |0 2 m OD ABABnAB AC ，所以1 2 450 2 m n ， 又 2 1 2 |0 2 n OE ACACmAB AC ，所以1 2 950 2 n m ， 联立方程组 1 2 450 2 1 2 950 2 m n n m ，解得 9 22 8 11 m n ， 所以 17 2 11 nm，故选 D 8【答案】D 【解析】如图所示， OA
12、OB OC0，所以O为 ABC的重心， 连AO并延长交BC与E，则E为BC的中点，延长AE至F，使AEEF，连BF，CF， 则四边形ABFC为平行四边形， 5 2 sincossinsinsin 2 aCBaAbBbC ， 2 5c ， 222 22 5 2 22 acb acabbc ac ，即 5 2 cb ， 又因为 2 5c ，所以4b， 4BFAC， 3 coscoscos 8 AFBCAECAO， 设AEx，则2AFx， 在ABF中由余弦定理得 2 22 cos 2 BFAFAB AFB BF AF ， 即 2 2 2 422 5 3 82 4 2 x x ，解得2x，即2AE 又
13、 2 955 sin1 cos1 648 CAECAE ， 155 22sin2 455 28 ABCAEC SSAEACCAE ， 故选 D 二、填空题 9【答案】4 【解析】由4AB ，6AC ，60BAC， 即有 1 4 6 cos602412 2 AB AC ， 则 111 () () 3 2 232 BF DEDFDBAEADDEABACAB 21121 96232 ACABABACAB 221 3 45 279 ACABAB AC 415 3616124 2739 ， 故答案为4 10【答案】 3 2 【解析】 121252 232363 BEBDDEABDCABACADABAC
14、， 所以 523 632 xy ， 故答案为 3 2 11【答案】0 【解析】如图，连AC，取AC的中点E，连ME，NE， 则,ME NE分别为ADC，CAB的中位线，所以 1 2 ENAB， 1 2 MEDC， 所以 1 () 2 MNMEENDCAB 由PQ与MN共线，所以()PQMNR， 故()()() () 2 PQABDCMNABDCABDCABDC 22 ()0 2 ABDC ， 答案0 12【答案】 1 ( ,2) 5 【解析】不妨设2BC ，3AC ， 由于A，P，N三点共线，M，P，B三点共线， 故由平面向量基本定理可设，(1)(1)CPCACNCCxyyBMx， 1 3 A
15、MAC， 1 2 BNBC， 2 (1)(1) 23 xy xy CBCBACPCAC， 2 1 3 1 2 xy x y ，解得 1 2 3 4 x y ， 11 24 CPCACB， 2 2 2 22 11 24 ()() CACB CPCP ABCBCACBCA 22 22 111 | | cos 4164 2| | cos CACBCACBCA CB CACBCACBCA CB 911 3 2 cos 106cos 1 444 4 492 3 2 cos13 12cos CA CB CA CB CA CBCA CB 12cos1333 11133 888 13 12cos13 12co
16、s CA CB CA CBCA CB ， 又1cos,1CA CB ， 2 11331 ()(,4) 8825 13 12cos, CP AB CA CB ， 1 ( ,2) 5 CP AB ， 故答案为 1 ( ,2) 5 13【答案】8,72 【解析】记, ,A B C所对边长分别为, ,a b c， 由正弦定理得2 sin a R A ，即 63 sin 22 55 a A R ，所以 4 cos 5 A ， 由余弦定理 222 2cosabcbcA ， 4 cos 5 A时， 22 88 362 55 bcbcbcbc，90bc，bc时等号成立， 所以 4 cos9072 5 AB A
17、CbcA uu u r uuu r ， 4 cos 5 A 时， 22 88 362 55 bcbcbcbc，10bc，bc时等号成立， 所以 4 cos108 5 AB ACbcA uuu r uuu r ， 综上 8,72AB AC ， 故答案为 8,72 14【答案】等腰三角形 【解析】2()()ADBDCDADDBADDCABAC，ABACBC， 由 20ABACADBDCD，即()BCABAC， 由四边形垂直平分可得ABC的是等腰三角形 15【答案】 4 5 【解析】1OAOBOC，3 45OAOBOC0，345OAOBOC ， 两边同时平方可得9 16 2425OA OB ， 0O
18、A OB ， 34 55 OCOAOB ， 则 84 55 AB ACOBOAOCOAOBOAOAOB 228484484 00 5555555 OB OAOBOAOB OA ， 故答案为 4 5 16【答案】7 【解析】由余弦定理得 222 1 +2cos4+162 4 212 2 BCABACAC ABA ， 222 ACABBC ，ABBC， 所以以B为原点，BC所在直线为x轴，建立如图所示的平面直角坐标系， 则(0,0)B，(2 3,0)C，(0,2)A，(2 ,0)Dx，( ,1),03M xx， (2 32 , 2)MBMCx，(2 , 2)ADx 2 2 3 ()2 (2 32 )444 3447 2 MBMCADxxxxx ， 当 3 2 x 时，()MBMCAD的最大值，最大值是7，故答案为7
