1、一、选择题1 （北京市朝阳区 2018 一模）如图，在平面直角坐标系 xOy 中，反比例函数 的图象xky经过点 T. 下列各点， ， ， 中，在该函数图象上的点有)64(，P)83(，Q)12(，M)48(，N（A）4 个（B）3 个（C ）2 个（D）1 个答案 B2、 （ 2018 年北京昌平区第一学期期末质量抽测）如图 ，点 B 是反比例函数（ ）在第一象限内图象上的一点，过点 B 作 BAx 轴于点 A，BCy 轴于点xky0C，矩形 AOCB 的面积为 6，则 k 的值为A3 B6 C-3 D-6答案：B答案：B3、 （2018 北京大兴第一学期期末）已知反比例函数 ，当 x0 时
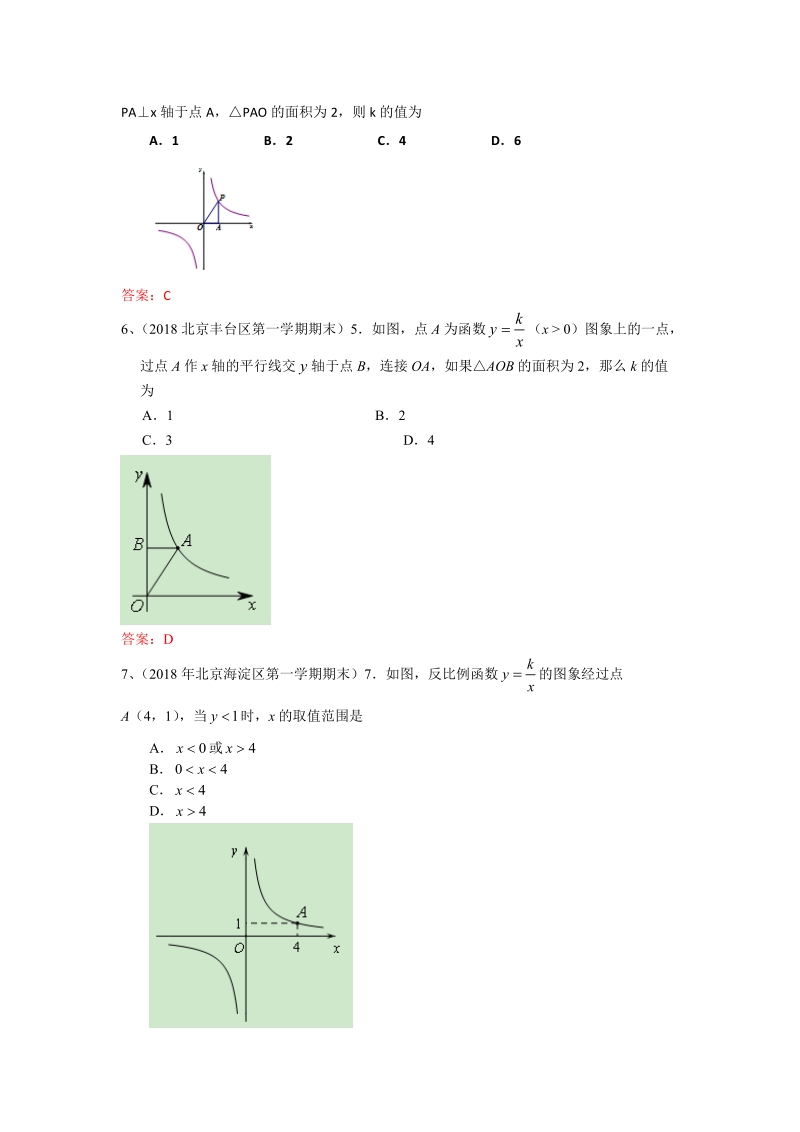
2、，y 随 x 的增xmy2大而增大，则 m 的取值范围是.m2 .m2 .m2答案：A4、 （ 2018 北京东城第一学期期末） 点 ， 都在反比例函数 的图象1,yAx2,B2yx上，若 ，则120x A B C Dy 120y 210y 120y 答案：C5、 （ 2018 北京房山区第一学期检测） 5. 如图，点 P 在反比例函数 的图象上，()kyxPAx 轴于点 A，PAO 的面积为 2，则 k 的值为A 1 B2 C4 D6 答案：C6、 （2018 北京丰台区第一学期期末）5如图，点 A 为函数 （x 0）图象上的一点，ky过点 A 作 x 轴的平行线交 轴于点 B，连接 OA，
3、如果AOB 的面积为 2，那么 k 的值y为A1 B2C3 D4答案：D7、 （2018 年北京海淀区第一学期期末）7如图，反比例函数 的图象经过点kyxA（4，1） ，当 时，x 的取值范围是1yA 或04BC xD 答案：A8、 （2018 北京密云区初三（上）期末）3.已知点 在反比例函数(1,m)2,nAB的图象上，则(0)kyxA. B. C. D. mn0nm00答案：A9、 （ 2018 北京平谷区第一学期期末） 7反比 例函数 的图象上有两点 ，2yx1Ax,y，若 x1x 2，x 1x20 ，则 y1y 2 的值是2B,y（A）正数 （B ）负数 （ C）0 （D）非负数答案
4、：B10、 （ 2018 北京顺义区初三上学期期末）4已知蓄电池的电压为定值，使用蓄电池时，电流 I(单位:A) 与电阻 R(单位:)是反比例函数关系，它的图象如图所示则用电阻 R 表示电流 I 的函数表达式为A B3IR6C D IR答案：D11、 （2018 北京通州区第一学期期末）若反比例函数的图象经过点 ，则该反比例函2,3数的表达式为（ ）A. B. C. D. xy6xy6xy3xy答案：B12、 （2018 北京西城区第一学期期末）点 ， 是反比例函数 图象上的1(,)A2(,)B6两点，那么 ， 的大小关系是（ ） 1y2A. B. C. D.不能确定12y12y答案：C13、
5、 （2018 北京燕山地区第一学期初四年级期末） 4若点 (x1，y 1)，( x 2， y 2) 都是反比例函数 图象上的点,并且 ,则下列结论中正确的是6yx120yAx 1 x2 Bx 1 x2Cy 随 x 的增大而减小 D两点有可能在同一象限答案： B 14、 如图， 已知点 P 为反比例函数 上一点， 过点 P 向坐标轴引垂线，6yx垂足分别为 M，N，那么四边形 MONP 的 面积为A 6 B3 C6 D12答案： C15、 （2018 北京燕山地区第一学期初四年级期末） 8如图， ABC 的三个顶点分别为 A(1，2) ，B (5，2)，C(5，5) 若 反 比 例 函 数 在
6、第 一 象 限 内 的 图 象 与 ABC 有 交 点，kyx则 k 的取值范围是A2 k 25 B 2 k 10C1 k 5 D10 k 25答案： A二、填空题9 （ 2018 北京石景山区初三毕业考试）对于函数 ，若 ，则 （填6yx2y3“”或“ y2，则 m 的取值范围是 .答案： b 时 ， n 的 取 值 范 围 .答案：21. 解：（1） 一次函数 的图象经过点 ， 1 分1yx(,2)Pm点 P 的坐标为(1 ，2). 2 分反比例函数 的图象经过点 P(1，2)，kyx3 分2k（2） 或 5 分0n240、 （2018 年北京海淀区第一学期期末）20码头工人每天往一艘轮船
7、上装载 30 吨货物，装载完毕恰好用了 8 天时间轮船到达目的地后开始卸货，记平均卸货速度为 v（单位：吨/天） ，卸货天数为 t（1）直接写出 v 关于 t 的函数表达式：v= ；（不需写自变量的取值范围）（2）如果船上的货物 5 天卸载完毕，那么平均每天要卸载多少吨？41、 （2018 年北京海淀区第一学期期末）23如图，函数 （ ）与 的kyx0yaxb图象交于点 A（-1，n）和点 B（-2 ，1） （1）求 k，a，b 的值；（2）直线 与 （ ）的图象交于点 P，与 的图象交于点 Q，xmkyx01y当 时，直接写出 m 的取值范围90PQ yxBAOxy 123423434234
8、Oxy 123423434234O解：（1） 函数 （ ）的图象经过点 B（-2， 1） ，kyx0 ，得 . 1 分122 函数 （ ）的图象还经过点 A（-1，n） ，kyx ，点 A 的坐标为（-1，2）. 2 分1n 函数 的图象经过点 A 和点 B，yaxb 解得 4 分,21.,3.（2） 且 . 6 分0m42、 （ 2018 北京怀柔区第一学期期末）20.在平面直角坐标系 xOy 中，直线 与双3x曲线 相交于点 A(m，2).xky(1)求反比例函数的表达式；(2)画出直线和双曲线的示意图；(3)若 P 是坐标轴上一点，且满足 PA=OA. 直接写出点 P 的坐标答案：解：(
9、1)直线 与双曲线 相交于点3xyxkyA（m，2）.A（1，2）1 分2 分xy(2)如图4 分(3)P(0，4)或 P(2，0) 6 分43、 （ 2018 北京门头沟区第一学期期末调研试卷）19已知二次函数 y = x2+2x3 .（1 ）将 y = x2+2x3 用配方法化成 y = a (xh) 2 + k 的形式； （2 ）求该二次函数的图象的顶点坐标.解：（1）y =x2+2x3=x2+2x+11 3 2 分=(x+1)24 3 分（2 ） y =(x+1)24，该二次函数图象的顶点坐标是（1，4 ） 5 分44、 （ 2018 北京门头沟区第一学期期末调研试卷）21.在平面直角
10、坐标 xOy 中的第一象限内，直线 与双曲的一个交点为 A（2，2）.10ykx（ ） 20myx（ ）（1 ） 求 k、m 的值；（2 ） 过点 且垂直于 x 轴的直线与 、的图象分别相交于点()P， 1ykx2mM、N ，点 M、N 的距离为 ，点 M、N 中的某一点与点 的距离为 ，如果1dP2d，在下图中画出示意图并且直接写出点 的坐标.12d解：（1）反比例函数 （ ）的图象过（2 ,2） ，2myx0k , 1 分2解得 4直线 的图象过（2,2 ） ，10ykx（ ） ，解得 2 分 2（2 ）示意图：正确 3 分xyOxy12345612345 NMOP xy123456123
11、45 NMO P5 分(22p,0)或 (,)45、 （2018 北京密云区初三（上）期末）22. 点 P(1，4)，Q（2， ）是双曲线 图mkyx象上一点.（1）求 k 值和 值.m（2）O 为坐标原点.过 轴上的动点 R 作 轴的垂线，交双曲线于点 S，交直线 于点xx OQT，且点 S 在点 T 的上方.结合函数图象，直接写 出 R 的横坐标 的取值范围.n（1）解：点 P(1，4)， Q（2， ）是双曲线 图象上一点. mkyx，4k， 3 分（2） 或 0n25 分46、 （ 2018 北京平谷区第一学期期末）22如图，在平面直角坐标系 xOy 中，函数 y= （k0，x0 ）的图
12、象与直线y=2x2 交于点 Q（2 ，m） y x-5-43-154321-54-32 54322O（1 ）求 m，k 的值；（2 ）已知点 P（a ，0 ） （a 0）是 x 轴上一动点，过点 P 作平行于 y 轴的直线，交直线y=2x2 于点 M，交函数 y= 的图象于点 Nk当 a=4 时，求 MN 的长；若 PMPN，结合图象，直接写出 a 的取值范围解：（1）直线 y=2x2 经过点 Q（2，m ） ，m=2 .1Q（2，2） 函数 y= 经过点 Q（ 2，2） ，kxk=4 2（2）当 a=4 时，P（4，0） 反比例函数的表达式为 y= .34xM（4,6） ，N（4,1） MN
13、=5 4 PMPN，a2 547、 （2018 北京石景山区第一学期期末）22在平面直角坐标系 xOy 中，一次函数的图象与 x 轴交于点 ，与反比例函数 的图象交于点 bxy)0,2(Axky),3(nB（1）求一次函数与反比例函数的表达式；（2）若点 P 为 x 轴上的点，且PAB 的面积是 2，则点 P 的坐标是 解：（1）一次函数 的图象与 x 轴交于点 A(2， 0)，yb 0可得， 2 1 分x当 时， ，31y点 B（3，1） 代入 中，可得 ，xk3反比例函数的表达式为 3 分xy（2）点 P 的坐标是(6，0)或（-2，0） .5 分48、 （ 2018 北京顺义区初三上学期
14、期末）25如图，在平面直角坐标系 xOy 中，直线与双曲线 （k0）相交于 A，B 两点，且点 A 的横坐标是 3 yxyx（1）求 k 的值；（2）过点 P（0，n）作直线，使直线与 x 轴平行，直线与直线 交于点 M，与双曲线2yx（k0）交于点 N，若点 M 在 N 右边，求 n 的取值范围解：（1）令 x=3，代入 ，则 y=1，2yxA（3，1 ） ，.1 分点 A（3，1 ） ，在双曲线 （k 0 ）上， x .3 分k（2）.4 分（画图）如图所示，当点 M 在 N 右边时，n 的取值范围是 或 6 分1n3049、 （2018 北京通州区第一学期期末）如图，在平面直角坐标系 中
15、，一次函数xOy与反比例函数 交于点 ， 0kbxy 0mxy2,3AaB,1（1）分别求出反比例函数和一次函数的表达式；（2）根据函数图象，直接写出不等式 的解集bk答案：50、 （2018 北京西城区第一学期期末）如图，在平面直角坐标系 xOy 中，双曲线（k0）与直线 的交点为 ， 两点，双曲线上一点 P 的横yx12yx(,1)Aa(2,)Bb坐标为 1，直线 PA，PB 与 x 轴的交点分别为点 M，N，连接 AN（1）直接写出 a，k 的值；（2）求证：PM=PN ， PMN答案：51、 （2018 北京燕山地区第一学期初四年级期末） 25如图，在平面直角坐标系 xoy 中，函数
16、(0)kyx时图象与直线 y=x+2 交于点 A( 3，m )（1）求 k，m 的值；（2） 已知点 P(a， b) 是直线 y=x 上， 位于第三象限的点，过点 P 作平行于 x 轴的直线， 交直线 y=x+2 于点 M，过点 P 作平行于 y 轴的直线，交函数的图象于点 N(0)kyx当 a= 1 时，判断线段 PM 与 PN 的数量关系，并说明理由；若 PN PM 结合函数的图象，直接写出 b 的取值范围答案： 解：（1）函数 的图象与直线)0(xky2xy交于点 A(-3,m). m=-3+2=-1, A(-3,-1). k=-1(-3)=3即 k 的值是 3，m 的值是-1 2（2）
17、当 a =-1 时，又点 P(a,b)是直线 y=x 上，P(-1,-1)令 y=-1，代入 , x=-3, M(-3,-1), PM=22xy令 x=-1,代入， y=-3,N(-1,-3),PN=2)0(k PM=PN 3-1b0 或 b-3 552、 （ 2018 北京昌平区二模）如图，在平面直角坐标系中，一次函数 与反比例函数xOy+(0)yaxb的图象交于点 A（4，1 ）和 B（ ， ） k（ 0） 1n（1 ）求 n 的值和直线 的表达式；yx（2）根 据这两个函数的图象，直接写出不等式的解集0kaxb答案解：（1）把点 A（4，1）代入 ，解得 k=4yx把点 B（-1，n）代
18、入 ，解得 1 分yx4n点 A（4，1）和 B（-1 ，-4）代入 得+(0)abkbxyO A B （第 22 题）解得 13kb 一次函数的表达式为 3 分3yx（2） 或 5 分1x0453、 （2018 北京朝阳区二模） 如图，在平面直角坐标系 xOy 中，直线 与函数61xky的图象的两个交点分别为 A（1，5） ，B.)0(2xky（1）求 的值；21,（2）过点 P（n，0）作 x 轴的垂线，与直线 61xky和函数 的图象的交点分别为点 M，N ，)(2ky当点 M 在点 N 下方时，写出 n 的取值范围.解：（1）A（1，5）在直线 上，61xky . 1 分1kA（1，5
19、 ）在 的图象上，)0(2xky . 2 分2k（2 ） 0 5. 5 分54、 （ 2018 北京东城区二模）22. 已知函数 的图象与函数 的图象交于点1yx0ykx.,Pm（1 ）若 ， 求 的值和点 P 的坐标；2nk（2 ）当 时，结合函数图象，直接写出实数 的取值范围 . k解：（1） ， ，或 ;-3 分12k2， 2，(2) . -5 分55、 （ 2018北京房山区二模）如图，在平面直角坐标系xOy中，直线 与双 ykxmyx2AO曲线 相交于点2-yxA（m ，2 ） （1）求直线 的表达式；k（2）直线 与双曲线 的另一个交点为yx2-yxB，点 P 为 x 轴 上 一
20、点 ， 若 ，直接写出 P 点 坐 标 AB解：（1）点 A(m,2)在双曲线 上，m= -1. 1A（-1，2）,直线 21ykx点 A（-1 ，2 ）在直线 上， 3-3yx（2） , 5150P21,56、 （ 2018 北 京 丰 台 区 二 模 ） 在平面直角坐标系 xOy 中，直线 l： . 21(0)ymx（1）判断直线 l 是否经过点 M（ 2，1） ，并说明理由；（2）直线 l 与反比例函数 的图象的交点分别为点 M，N ，当 OM=ON 时，直接写出点 N 的坐kyx标. （1）解：直线 l 经过点 M（2，1）. .1 分理由如下：对于 ，令 x=2，则 1ymx21ym
21、直线 l 经过点 M（2，1）. .2 分441123213xOy432432（2）点 N 的坐标为（1， 2） ， （-2，-1） ， （-1 ，-2）. .5 分57、 （ 2018 北 京 海 淀 区 二 模 ） 已知直线 过点 ，且与函数 的图象相交于l(,2)P(0)kyx两点，与 轴、 轴分别交于点 ，如图所示，四边形 均为矩形，,ABxyCD,ONAEFBM且矩形 的面积为 .OFM3（1 ）求 的值；k（2 ）当点 的横坐标为 时，求直线 的解析式及线段 的BlBC长；（3 ）如图是小芳同学对线段 的长度关系的思考示意图.,ADBC记点 的横坐标为 ，已知当 时，线段 的长Bs
22、23sB随 的增大而减小，请你参考小芳的示意图判断：当s时，线段 的长随 的增大而 . 3Cs（填“增大” 、 “减小”或“不变 ”）答案解：（1）设点 B 的坐标为（x，y） ，由题意得： ，BFy.M 矩形 OMBF 的面积为 3， . 3xy B 在双曲线 上，kx . k（2） 点 B 的横坐标为 3，点 B 在双曲线上， 点 B 的坐标为（3，1）.设直线 l 的解析式为 .yaxb 直线 l 过点 ，B （3，1） ，(2,)P 解得31.ab,4. 直线 l 的解析式为 . yx 直线 l 与 x 轴交于点 C（4，0） ，lPNM FED CBAyxO . 2BC（3） 增大
23、58、 （2018 北京西城区二模）如图，在平面直角坐标系 xOy 中，函数 （ ）的myx0图象经过点 ，AB x 轴于点 B，点 C 与点 A 关于原点 O 对称， CDx 轴于(4,)An点 D，ABD 的面积为 8.（1）求 m，n 的值；（2）若直线 （k0）经过点 C，且与 x 轴，y 轴的交点分别为点 E，F，当yxb时，求点 F 的坐标2CFE解：（1）如图 4. 点 A 的坐标为，点 C 与点 A 关于原点 O 对称， 点 C 的坐标为 ABx 轴于点 B，CDx 轴于点 D， B，D 两点的坐标分别 为 ， ABD 的面积为 8， ， 解得 2 分 函数（）的图象经过点， 3分（2）由（1）得点 C 的坐标为 如图 4，当时，设直线与 x 轴，y 轴的交点分别为点， 由 CDx 轴于点 D 可得 CD CDO ， 图 4 点的坐标为 如图 5，当时，设直线与 x 轴，y 轴的交点分别为点， 同理可得 CD， ， 为线段的中点， 2OFDC 点的坐标为6 分综上所述，点 F 的坐标为， 图 5
