1、20222022 年中考数学热身模拟试卷（年中考数学热身模拟试卷（7 7） 一、选择题：（以下每个小题均有一、选择题：（以下每个小题均有 A、B、C、D 四个选项，其中只有一个选项正确，请用四个选项，其中只有一个选项正确，请用 2B2B 铅笔在答题铅笔在答题 卡相应位置作答，每小题卡相应位置作答，每小题 3 3 分，共分，共 3636 分）分） 1.计算（-2）x（-4）的结果是（ ） 8 -8 -6 6 2.下列不是正方体表面展开图的是（ ） 3.下列运算正确的是（ ） 4.如图，1=2，3与4互补，则下列结论中错误的是（ ） BC AB = EF DE DF AB = AC DE AC B
2、C = DF FE DE AB = DF AC 5.下列说法正确的是（ ） 五名学生在某次测体温时得到：36.2，36.3，36.3，36.5，36.5，这组数据的众数是 36.5. 方差越大，数据的波动越大，方差越小，数据的波动越小. 确定性事件一定发生. 为了解一批灯泡的寿命，应采用全面调查方式. 6.如图， ABC 是锐角三角形，AD、AE、AF 分别是 ABC 的中线、角平分线、高线，则下列点一定在 AE 上的是（ ） 重心 内心 外心 垂心 （第 4 题图） （第 6 题图） (A) (B) (C) (D) (A) (D) (B) (C) (A) (B) (C) (D) (A) (B
3、) (C) (D) (A) (B) (D) (C) (A) (B） (C) (D) 222 4)2(baba 248 xxx1037 4 2 22 813xx (第 10 题图) （第 11 题图） AB C O o AB C y x y2y1 7.如图，点是双曲线 1 y= x 4 （x0）上的一点， 2 y= x k 与 1 y= x 4 的图像关于 y 轴对称，过点 A 作 AB/X 轴交 2 y= x k 的图像于点 B，点 C 是 x 轴上一点，连接 AC、BC，则ABC 的面积为（ ） 16 8 4 2 8.若用科学记数法表示为 1.810 12，则 n 的值是（ ） 10 11
4、12 13 9. 如图，以扇形 ACB 上一点 O 为圆心作圆，使圆经过 A、B、C 三点，已知O 的半径是 4，连接 OB, OCB=60 0 ，若将扇形 ABC 剪下，围成一个圆锥，则此圆锥的底面积是（ ） 3 2 9 25 9 36 9 16 10.如图，在平行四边形 ABCD 中，AB=2.ABC=60 ,按以下步骤作图：以 B 为圆心，AB 长为半径画 弧，交 BC 于点 E;分别以 A、E 为圆心，大于 2 1 AE 长为半径画弧，两弧交于点 M; 连接 BM 交 AD 于点 F，过点 A 作 AHBF 于点 H，则 BF 的长是（ ） 43 33 23 3 11.如图，直线 y=
5、-2x+4 与两坐标轴分别交于 A、B 两点，点 C 是直线 AB 上一点，且横坐标为-1，过点 C 的直线bxy 2 1 交 x 轴于点 D,则三角形 ADC 的面积为（ ） 45 42 43 44 12.在平面直角坐标系中，图是抛物线 y=x43 2 x（-1x4）的图象，现将图绕原点 O 旋转 180 0 得到图,若直线 y=-x+m 与图、有三个交点，则 m 的取值范围是（） -5m-1 或 1m5 -4m-1 或 1m4 -5m-2 或 2m5 -2m-4 或 2m4 （第 7 题图） （第 9 题图） （第 12 题图） (A) (B) (D) (C) (A)(B) (D) (C)
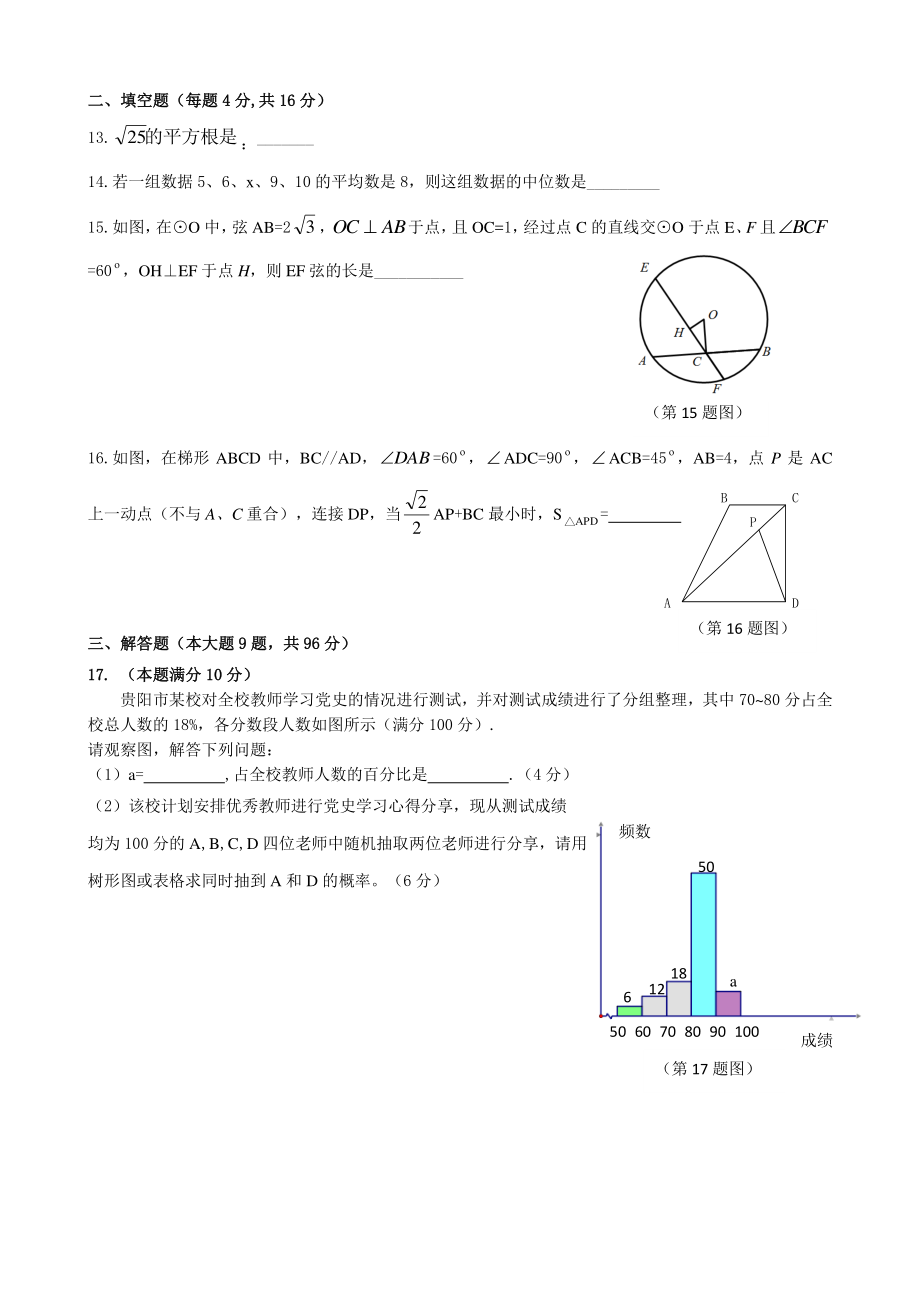
6、 (A) (B) (D) (C) (A) (B) (D) (C) (A) (B) (D) (C) (A) (B) (D) (C) （第 15 题图） （第 17 题图） 二、填空题（每题二、填空题（每题 4 4 分分, ,共共 1616 分）分） 13.的平方根是25 ：_ 14.若一组数据 5、6、x、9、10 的平均数是 8，则这组数据的中位数是_ 15.如图， 在O 中， 弦 AB=23，ABOC 于点， 且 OC=1， 经过点 C 的直线交O 于点 E、F 且BCF =60 ，OHEF 于点 H，则 EF 弦的长是_ 16.如图，在梯形 ABCD 中，BC/AD，DAB=60 ， AD
7、C=90 ， ACB=45 ，AB=4，点 P 是 AC 上一动点（不与 A、C 重合），连接 DP，当 2 2 AP+BC 最小时，S APD = 三、三、解答题（本大题解答题（本大题 9 9 题，共题，共 9696 分）分） 17.17. （本题满分（本题满分 1010 分）分） 贵阳市某校对全校教师学习党史的情况进行测试，并对测试成绩进行了分组整理，其中 7080 分占全 校总人数的 18%，各分数段人数如图所示（满分 100 分）. 请观察图，解答下列问题： （1）a= ,占全校教师人数的百分比是 .（4 分） （2）该校计划安排优秀教师进行党史学习心得分享，现从测试成绩 均为 100
8、 分的 A,B,C,D 四位老师中随机抽取两位老师进行分享，请用 树形图或表格求同时抽到 A 和 D 的概率。（6 分） （第 16 题图） A BC D P 频数 50 6 12 18 a 成绩 50 60 70 80 90 100 （第 19 题图） （第 20 题图） （第 18 题图） 18.18.（本题满分（本题满分 1010 分）分） 学习三角函数后，爱探究的小吴在锐角ABC 中作如下图推导： 解：过 A 作 ADBC 于 D， AC AD C sin , AC CD C cos inCACADs ， CACcoCDs 222 BDADAB 222 )(CDBCADAB CACBC
9、CACBCCACABcos.2cossin 222222 22222 cossincos.2ABBCCCACCACBC）（ 易证 1cossin 22 CC （1）根据上述推导，Bcos （2）若 AC5，AB7，BC39，根据（1）的结论求A 的度数。 19.19.（本题满分（本题满分 1010 分）分） 如图，已知平行四边形 ABCD，BC=2AB，过点 C 作 CEDC 交 AB 于点 E，点 M 是 AD 的中点，延 长 EM 交 CD 的延长线于点 G，连接 EM,CM. （1）求证：EM=CM（5分） （2）当AEM= 45时，求EMD的度数.（5分） 20.20.（本题满分（本题
10、满分 1010 分）分） 某市一处有在同一直线上的如图 三栋高楼（从左到右依次为 A、B、C）， 在 A 楼的最高处 A 点测得 B 楼的最高处 B 点的仰角BAD=63.5 0，在 C 楼的最高 处 C 点测得 B 楼的最高处 B 点的仰角 BCE=71.6 0，已知 FG 比 GH 宽 1 米,DE=16 米， ADBG,CEBG,求 B 楼比 C 楼高多少米？（结果保留整数） （参考数据：0 . 25 .63tan 0 ，0 . 36 .71tan 0 ） 58 222 )cos()sin(CACBCCACAB BCAC ABBCAC C .2 cos 222 21.21.（本题满分（本
11、题满分 1010 分）分） 如图，在反比例函数 y= x 6 图像上有两个动点 A、B，过点 A、B 分别作 y 轴、x 轴的平行线交于点 M. （1）若直线 y=x+1 与 y= x 6 （x0）交于一点，求该点的坐标.（5 分） （2）试判断 SBOM 与 SAOM 的关系并证明.（5 分） 22.22.（本题满分（本题满分 1212 分）分） 在脱贫攻坚中，某县对城西学府家园某栋楼的 100 平方米和 120 平方米的两种规格套房进行装修。经 预算，共需资金 350 万元。已知装修两套 100 平方米和三套 120 平方米的套房共用资金 61 万元，装修三 套 100 平方米和五套 12
12、0 平方米的套房共用资金 98 万元. （1）若已知该栋楼 120 平方米的套房不多于 10 套，则 100 平方米的套房至少有多少套？（5 分） （2）有一位爱心人士愿意捐款与政府一道对该栋楼的两种套房装修 20 套，若爱心捐款投入装修不多于 150 万元，政府投入装修不低于 85 万元，其中爱心捐款用于 100 平方米和 120 平方米的每套装修分别为 7 万元和 8 万元，试计算有多少种装修方案？写出计算过程.（5 分） 23.23.（本题满分（本题满分 1212 分）分） 如图，以 Rt ABC 的斜边 AB 的中点 O 为圆心作O，点 D 时弧 BC 的中点，连接 CD,OD、AD
13、分别 交 BC 于点 E、F,CG 是O 的切线，G=BCD （1）求证：AGCDAC 2 （6 分） （2）若 tanCAD 3 2 ，求 cosCDA 的值（6 分） （第 21 题图） （第 23 题图） 图 24.24.（本题满分（本题满分 1212 分）分） 如图：抛物线 yax2+bx+c（a0）与 x 轴交于点 A，B两点，OB:OA=1:3,与 y 轴交于点 C,OA=OC=3, 点 G 为抛物线的顶点. （1）求这条抛物线的函数表达式；（4 分） （2）求ADC 的周长（4 分） （3）点 P 是抛物线上的一个动点，过点 P 作 PEX 轴于点 E，在抛物线上是否存在点 P，
14、使得PAE 与OBC 相似？若存在，求出点 E 的坐标，若不存在，请说明理由.（4 分） 25.25.（本题满分（本题满分 1212 分）分） （1） 知识积累： 如图， ACB=AOB= 90， CA 交 OA 于点 A， CB 交 OB 于点 B， OC 平分AOB， 求证：AC=BC；（4 分） （2）知识迁移：如图，AOB=120 ，ACB=60，CA 交 OA 于点 A，CB 交 OB 于点 B，OC 平 分AOB，判断线段 OA、OB、OC 三者之间的关系并证明；（4 分） （3） 知识探索： 如图， AOB=2， ACB=180 -2， CA 交 OA 于点 A， CB 交 OB
15、 于点 B， AC=BC. 探索线段 OA、OB、OC 与 的关系并证明.当 OA=. 2 3 , 3, 2 3 时，求OCOB（4 分） 图 图 （第 24 题图） （第 25 题图） 数学答案数学答案 一、选择题答案：1.A;2.D;3.B;4.B;5.B;6.B;7.C;8.B;9.D;10.C;11.A;12.B. 二、填空题答案：（13）.5；（14）. 9 ；（15）.15；（16）.32. 解析: 11.由直线 y=-2x+4 可知 A(2,0),B(0,4) C 点的横坐标为-1 且点 C 在直线 y=-2x+4 上 点 C 为(-1,6) 直线 CD 为 y= 2 1 x+b
16、 6=）（ 1- 2 1 +b b= 2 13 直线 CD 与 X 轴的交点为(-13,0)，则 AD=15 ADC S= 2 1 156=45 12.如图，图是由图y=x 2 -3x-4(-1x4)绕原点旋转 180 而得到 图的解析式为 y=-x 2 -3x+4(-4x1) (1)当直线 y=-x+m 与图只有一个交点时， 则 x 2 -3x-4=-x+m 有两个相 等的实数根 =0 时，即 4+4（4+m）=0,解得 m=-5 此时 y=-x-5 与图没有交点， 此时直线与图只有一个交点。 (2) 当直线y=-x+m经过点(-4,0)时，直线y=-x-4与图有两个交点，与 图有一个交点，
17、此时直线与图只有三个交点。 (3) 当直线y=-x+m经过点(-1,0)时，直线y=-x-1与图有两个交点、与 图有一个交点，此时直线与图只有三个交点。 故要使直线 y=-x+m 与图图有三个交点，则-4m1 又图与图关于原点对称 当 1m4 时，直线 y=-x+m 与图图也有三个交点 综上所述，m 的取值范围是-4m1 或 1m4 15.连接 OB.OE OCAB,AB=23 BC= 2 1 AB=3 在 RtBOC 中，OC=1,OCB=90 OB= 22 BCOC =13=2 OHEF 于点 H,则 EF=2EH BCF=60 OCA=90 OCE=30 OC=1,OMC=90 OH=
18、2 1 OC= 2 1 在 RtOEH 中OHE=90 ,OE=OB=2 EH= 22 OMOE = 22 ) 2 1 (2 = 2 15 EF=2EH= 2 15 2=15 16、过点 B 作ADBE 于点 E.交 AC 于点 P，则 0 90BEABED. BPBC BPCBCPAPBCAE CBEACBCAD ACBADBC 0 00 0 45. 2 2 90.45 90./ 既为所找点。最短，故最短，即 三点共线 PBCAPPEBP EPB 2 2 . 32232 2 1 2 1 322232 232 90 232 2, . 32 4,60,90 0 00 PEADS DP EDAEA
19、D BCDE BEDC CBEADCBED PEBEBPBC PEAEBE ABBADAEBABERt APD 连接 是矩形四边形 中，在 17.(1) 14 人 14% (4 分) （2） 答：同时抽到 A 和 D 的概率为 6 1 （10 分） E A BC D P P 分）画出树形图或表格（3 18 题 （3）根据上述推导，Bcos BCAB ACBCAB 2 222 （4分） （4）若AC5，AB7，BC39，根据（1）的结论求A的度数。 由推导易得 ACAB BCACAB A .2 cos 222 （6 分） AC5，AB7，BC39 572 )39(57 cos 222 A 2 1
20、 （8 分） 19.证明：（1）如图 四边形 ABCD 是平行四边形，点 M 是线段 AD 中点 AM=DM，ABCD 延长 EM 与 CD 的延长线交于点 G (1 分) ABCG，1=AEM 5=6 AEMDGM（AAS）（3 分） EM=GM 又ECCD EGC 是直角三角形 EM=CM 4=8 EM=CM （5 分） （2）由（1）可知AEMDGM，EGC 是直角三角形，且点 M 是斜边中点 1=AEM=3 （6 分） 在平行四边形 ABCD 中 BC=2AB CD=MD 2=3 在MGC 中，EMC=1+3 EMD=3AEM（8 分） 当AEM=45 o 时，EMD=3AEM=345
21、 o =135 o （10 分） 20. 解：设 BC 两栋楼间的距离为 a 米，B 楼比 A 高 x 米，由题意得 1 5 .6 3t a n 0 a x ， a x16 6 .71tan 0 （4 分） 0 . 25 .63tan 0 ，0 . 36 .71tan 0 ) 1(2ax ax316 解得： ， （8 分） 38+1654(米) 38x18a 分）（ 10600 A B 楼比 C 高 54 米.（10 分） 21.解：（1）由题可知，直线y=x+1 与 y= x 6 （x0）交于一点 x+1= x 6 （1 分） 解得 x1=2,x 2=-3(舍去)（3 分） 当 x=2 时，
22、y=x+1=2+1=3 该点坐标为（2,3）（5 分） （2）根据题意可知：AMy 轴，BMx 轴，A、B 两动点在y= x 6 （x0）的图像上 设点 M 坐标为（a,b）（6 分） 点 A 坐标为（a, a 6 ），点 B 坐标为（b b ， 6 ）（7 分） SAOM= 2 1 AM M x3 2 b)a- a 6 ( 2 1 ab （8 分） SBOM= 2 1 BM M y3 2 ab -a)b- b 6 ( 2 1 （9 分） SAOM=SBOM（10 分） 22.解：（1）设装修一套 100 平方米的套房用资金x万元，装修一套 120 平方米的套房用资金y万元，由题 意得： 2x
23、+3y61 3x+5y98 （2 分） 解得 x11 y13 （3 分） 设 100 平方米的套房至少有a套，由题意得 11a+1310350 解得a20 答：100 平方米的套房至少有 20 套。（6 分） （2）设装修 100 平方米的套房共b套，则装修 120 平方米的套房共）（b20套，由题意得 7b8(20b）150 （11-7）b（13-8）（20 - b）85 （9 分） 解得 10b15 共有 6 种装修方案。（12 分） 24 解： （1）证明：连接 OC，如图 1 所示： ACB90， ABC+CAB90， OA=OC，CDA=OBC CAB=ACO ACO+CDA=90
24、（2 分） CG 是O 的切线 ACG+ACO=90 ACG= CDA 点 D 是弧 BC 的中点 弧 CD=弧 BD CAD=BAD G=BCD=BAD G=CAD ACGCDA（5 分） 2 AC=CD.AG（6 分） （2）解：如图：点 D 是弧 BC 的中点 ODBC （7 分） 由 tanCAD= 3 2 ,则 tanCAD=tanCBD= 3 2 BE DE ,可设 DE=2a,BE=3a,设O 的半径为 r,则 OB=r， OE= r-2a. （9 分） 在 RtBOE 中， 222 OBBEOE即（ 22 2 )3()2(raar，解得 r=a 4 13 （11 分） 在 Rt
25、BOE 中，cosOBE=CDA= 13 12 4 13 3 a a OB BE （12 分） 24.24.（本题满分（本题满分 1010 分）分） 解：（1）由题可得：OA=OC=3 点 A 的坐标为（-3,0），点 C 的坐标为（0,-3） OB:OA=1:3 点 B 的坐标为（1,0） （2 分） 设抛物线解析式为：)0( 2 acbxaxy 把 A、B、C 三点坐标代入得： 解得：a=1,b=2,c=-3 抛物线解析式为：3-2 2 xxy （4 分） （2）OA=OC=3 AC=2333 2222 OCOA 由413-2 2 2 ）（xxxy 点 D 坐标为（-1,-4） （6 分）
26、 AD=5242)()( 2222 DADA yyxx CD=211)()( 2222 DcDc yyxx 三角形 ADC 周长=5224 （8 分） （3）存在，理由如下： （9分） 设点 P 坐标为) 32,( 2 mmm 如图：当AEPBOC 时： OC EP BO AE 解得：4, 2 21 mm 2143-2ymym时，；当时，当 如图：当AEPCOB 时： OB EP CO AE 解得： 3 2 , 3 4 21 mm 9 11 3 2 9 13 3 4 ymym时，；当时，当 综上可得 P 的坐标为），（ 9 13 3 4 或），（ 9 11 - 3 2 或），（ 214），（3
27、-2- （12 分） 25. 解： 3 0 039 c cba cba 3 3-2 1 3 2 mm m 1 3-2 3 3 2 mm m （1）如图，过点 C 作 CEOB 于点 E，过点 C 作 CFOA 的延长线于点 F. CFA=CEB=90 0 （1 分） OC 平分AOB，CF=CE 在四边形 AOBC 中，AOB=ACB=90 0,CAO+CBO=1800 （2 分） 又CAO+CAF=180 0，CAF=CBO CAFCBE（AAS） AC=BC （4 分） (2).如图，过点 C 作 CGOB 的延长线于点 G，过点 C 作 CHOA 的于点 H. CHA=CGB=90 0
28、OC 平分AOB，CH=CG （5 分） 在四边形 AOBC 中，AOB=120 0，ACB=600 AOB+ACB=180 0,CAO+CBO=1800 又CBG+CBO=180 0，CBG=CAH CAHCBG（AAS） AH=BG 又OC 平分AOB，CGOB 的延长线于点 G，CHOA 的于点 H. HCOGCO（AAS）（6 分） HO=GO HO=OB+BG AO+BO=2GO 在 RtOGC 中，COG=60 0 OCG=30 0，OC=2GO,AO+BO=OC.（8 分） （3）如图，过点 C 作 CNOA 的延长线于点 N，过点 C 作 CMOA 的于点 M. CNA=CMB
29、=90 0 在四边形 AOBC 中，AOB=2，ACB=180 0 -2 AOB+ACB=180 0, CAO+CBO=180 0 又CAN+CAO=180 0， CBO=CAN CA=CB CANCBM（AAS）（10 分） MB=AN,CN=CM OC 平分AOB COM=COA= 易得： CONCOM OM=ON AO+OB=2OM 在三角形 OCM 中，COS .2OC= OC OM .2OC=2OM OA+OB=2OCCOS COS= OC OBOA 2 当 OA=时： 2 3 , 3, 2 3 OCOB COS= 2 3 2 3 2 3 2 3 2 OC OBOA 0 30 （12 分）
