 2017-2018学年高中人教A版数学必修4:第27课时 两角差的余弦公式课时作业(含答案解析)
2017-2018学年高中人教A版数学必修4:第27课时 两角差的余弦公式课时作业(含答案解析)
《2017-2018学年高中人教A版数学必修4:第27课时 两角差的余弦公式课时作业(含答案解析)》由会员分享,可在线阅读,更多相关《2017-2018学年高中人教A版数学必修4:第27课时 两角差的余弦公式课时作业(含答案解析)(5页珍藏版)》请在七七文库上搜索。
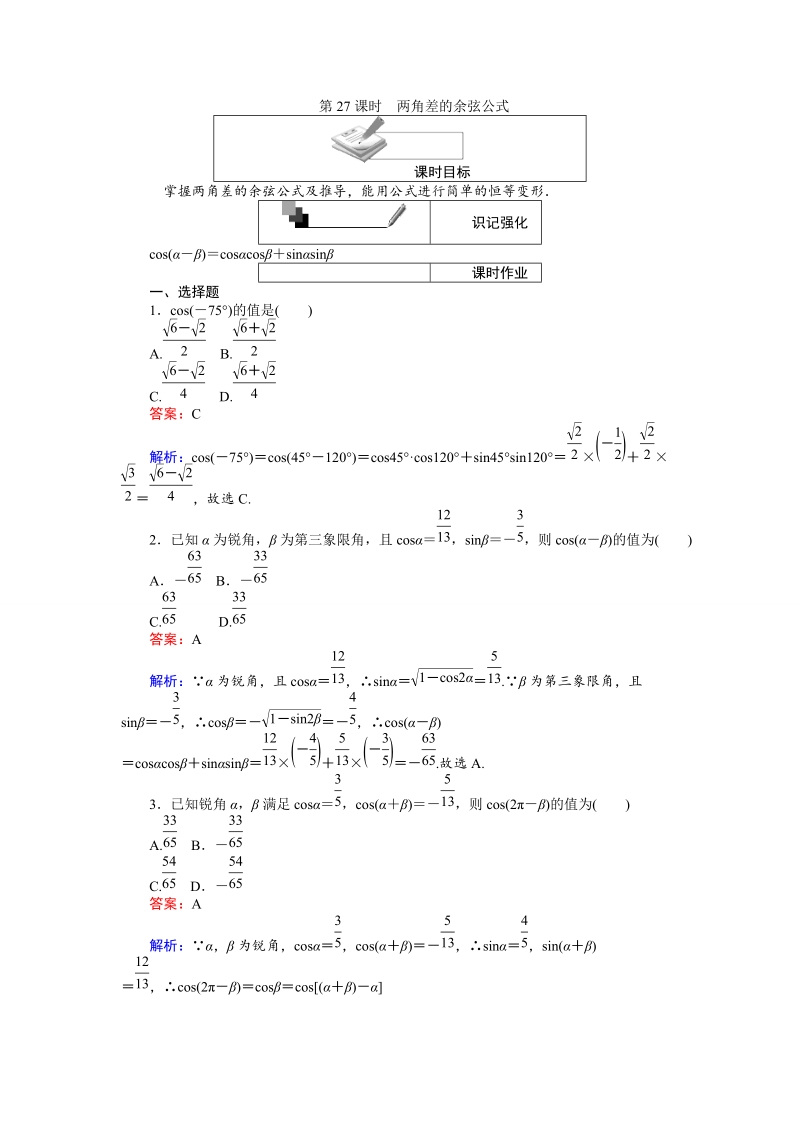
1、第 27 课时 两角差的余弦公式课时目标掌握两角差的余弦公式及推导,能用公式进行简单的恒等变形识记强化cos( )coscos sin sin课时作业一、选择题1cos(75)的值是 ( )A. B.6 22 6 22C. D.6 24 6 24答案:C解析:cos(75) cos(45 120)cos45cos120sin45sin120 22 ( 12) 22 ,故选 C.32 6 242已知 为锐角, 为第三象限角,且 cos ,sin ,则 cos() 的值为( )1213 35A B6365 3365C. D.6365 3365答案:A解析: 为锐角,且 cos ,sin . 为第三
2、象限角,且1213 1 cos2 513sin , cos ,cos()35 1 sin2 45coscos sinsin .故选 A.1213 ( 45) 513 ( 35) 63653已知锐角 , 满足 cos ,cos() ,则 cos(2) 的值为( )35 513A. B3365 3365C. D5465 5465答案:A解析:, 为锐角,cos ,cos() ,sin ,sin()35 513 45 ,cos(2 )coscos( ) 1213cos()cossin()sin .513 35 1213 45 33654在ABC 中,若 sinAsinB0.即 cos(AB )0,cosC0 , cosC0,所以 0m 2 ,解得 m .72 142 142coscos 的取值范围是 . 142,142


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2017 2018 年高 中人 数学 必修 27 课时 两角差 余弦 公式 作业 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-30029.html