1、2020年江苏省南通市中考数学模拟试卷五一选择题（共11小题，每小题3分，共33分）1绝对值小于4的所有整数的和是（）A4B8C0D12地球的表面积约为510000000km2，将510000000用科学记数法表示为（）A0.51109B5.1108C5.1109D511073下列图形是轴对称图形的有（）A2个B3个C4个D5个4下列计算正确的是（）A3a+2b5abB5a22a23C7a+a7a2D2a2b4a2b2a2b5下列各组数不可能是一个三角形的边长的是（）A7，8，9B5，6，7C3，4，5D1，2，36在一次科技知识竞赛中，两组学生成绩统计如下表，通过计算可知两组的方差为S甲21
2、72，S乙2256下列说法：两组的平均数相同；甲组学生成绩比乙组学生成绩稳定；甲组成绩的众数乙组成绩的众数；两组成绩的中位数均为80，但成绩80的人数甲组比乙组多，从中位数来看，甲组成绩总体比乙组好；成绩高于或等于90分的人数乙组比甲组多，高分段乙组成绩比甲组好其中正确的共有（）分数5060708090100人数甲组251013146乙组441621212A2种B3种C4种D5种7若圆的半径为R，圆的面积为S，则S与R之间的关系式为（）AS2RBSR2CS4R2DS8骆驼被称为“沙漠之舟”，它的体温是随时间的变化而变化的，在这一问题中，因变量是（）A沙漠B体温C时间D骆驼9直角三角形纸片的两直
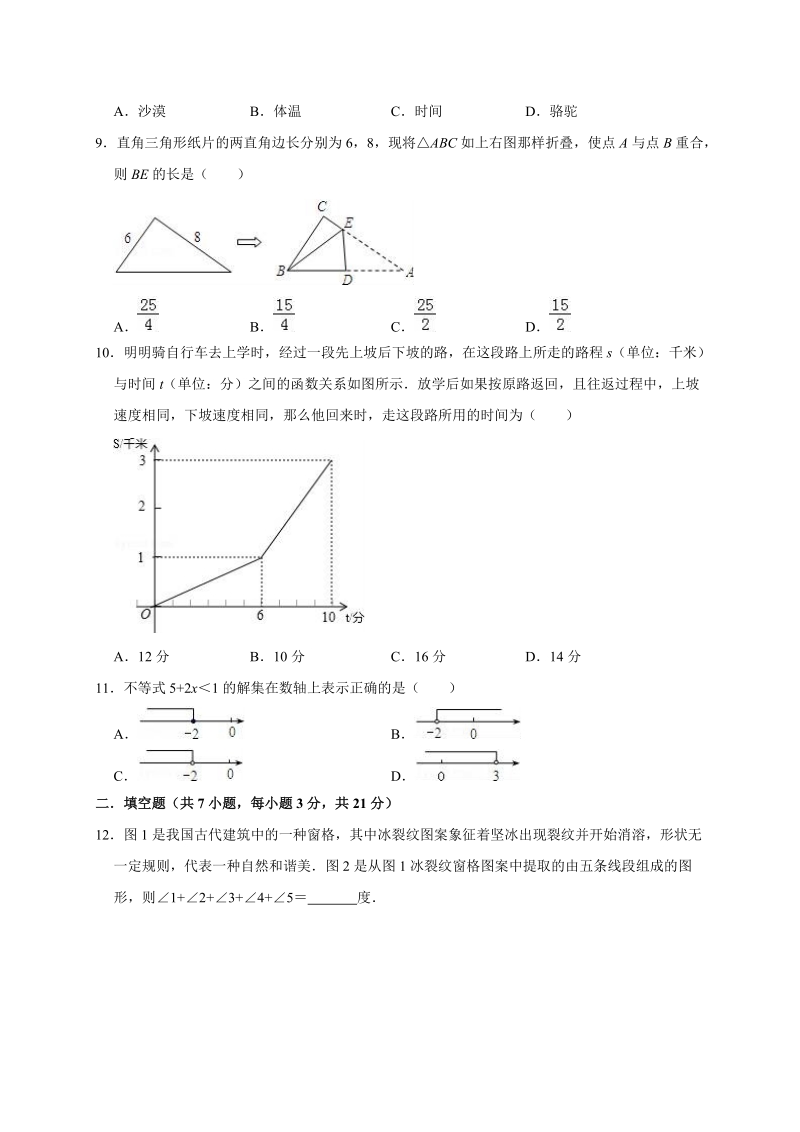
3、角边长分别为6，8，现将ABC如上右图那样折叠，使点A与点B重合，则BE的长是（）ABCD10明明骑自行车去上学时，经过一段先上坡后下坡的路，在这段路上所走的路程s（单位：千米）与时间t（单位：分）之间的函数关系如图所示放学后如果按原路返回，且往返过程中，上坡速度相同，下坡速度相同，那么他回来时，走这段路所用的时间为（）A12分B10分C16分D14分11不等式5+2x1的解集在数轴上表示正确的是（）ABCD二填空题（共7小题，每小题3分，共21分）12图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美图2是从图1冰裂纹窗格图案中提取
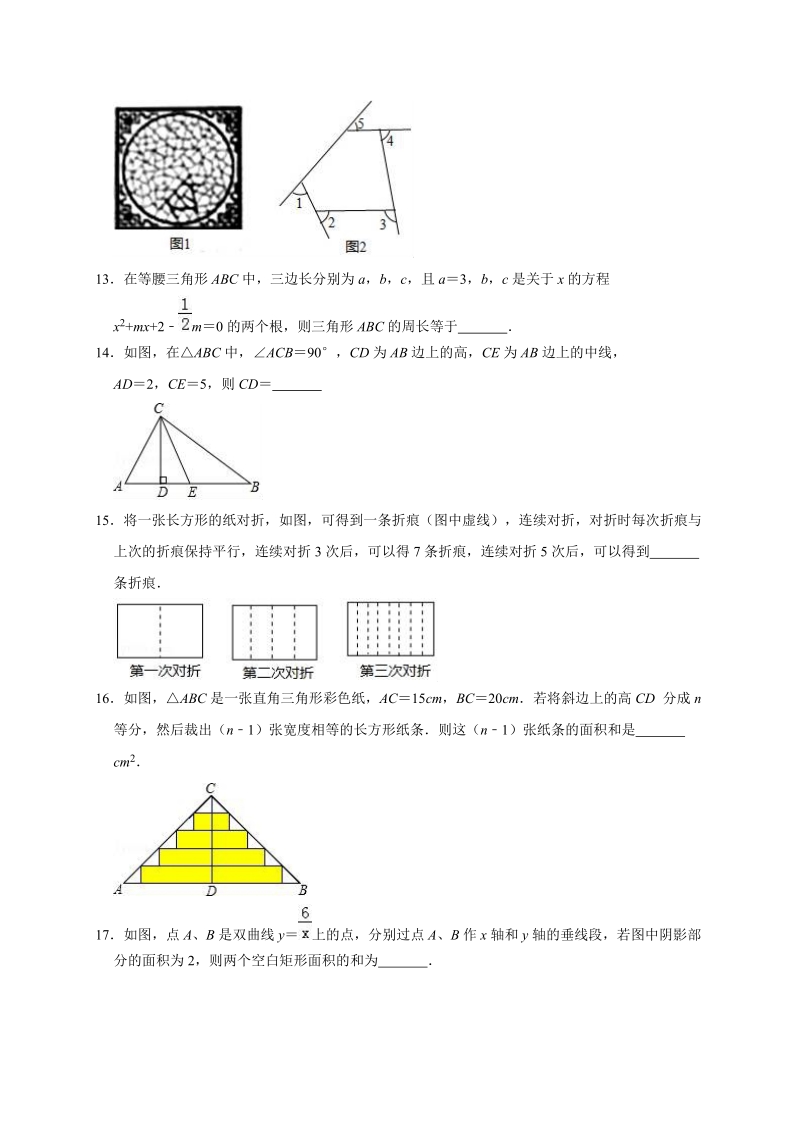
4、的由五条线段组成的图形，则1+2+3+4+5 度13在等腰三角形ABC中，三边长分别为a，b，c，且a3，b，c是关于x的方程x2+mx+2m0的两个根，则三角形ABC的周长等于 14如图，在ABC中，ACB90，CD为AB边上的高，CE为AB边上的中线，AD2，CE5，则CD 15将一张长方形的纸对折，如图，可得到一条折痕（图中虚线），连续对折，对折时每次折痕与上次的折痕保持平行，连续对折3次后，可以得7条折痕，连续对折5次后，可以得到 条折痕16如图，ABC是一张直角三角形彩色纸，AC15cm，BC20cm若将斜边上的高CD 分成n等分，然后裁出（n1）张宽度相等的长方形纸条则这（n1）张
5、纸条的面积和是 cm217如图，点A、B是双曲线y上的点，分别过点A、B作x轴和y轴的垂线段，若图中阴影部分的面积为2，则两个空白矩形面积的和为 18ABC在平面直角坐标系中的位置如图A、B、C三点在格点上（1）作出ABC关于x轴对称的A1B1C1，并写出点C1的坐标 ；（2）在y轴上找点D，使得AD+BD最小，作出点D并写出点D的坐标 三解答题（共10小题，共66分）19设 x、y 是有理数，且 x，y 满足等式x2+2y+y174，求xy的值20先化简，再求值：（1）+x，并将你喜欢的值代入计算（2），其中a，b21为了解某校九年级男生的体能情况，体育老师从中随机抽取部分男生进行引体向上测
6、试，并对成绩进行了统计，绘制成尚不完整的扇形图和条形图，根据图形信息回答下列问题：（1）本次抽测的男生有 人，抽测成绩的众数是 ；（2）请将条形图补充完整；（3）若规定引体向上6次以上（含6次）为体能达标，则该校125名九年级男生中估计有多少人体能达标？22从化市某中学初三（1）班数学兴趣小组为了解全校800名初三学生的“初中毕业选择升学和就业”情况，特对本班50名同学们进行调查，根据全班同学提出的3个主要观点：A高中，B中技，C就业，进行了调查（要求每位同学只选自己最认可的一项观点）；并制成了扇形统计图（如图）请回答以下问题：（1）该班学生选择 观点的人数最多，共有 人，在扇形统计图中，该观
7、点所在扇形区域的圆心角是 度（2）利用样本估计该校初三学生选择“中技”观点的人数（3）已知该班只有2位女同学选择“就业”观点，如果班主任从该观点中，随机选取2位同学进行调查，那么恰好选到这2位女同学的概率是多少？（用树形图或列表法分析解答）23如图，在菱形ABCD中，E为AD中点，EFAC交CB的延长线于F求证：AB与EF互相平分24如图，小明在大楼30米高（即PH30米）的窗口P处进行观测，测得山坡上A处的俯角APQ为15，山脚B处的俯角BPQ为60，已知该山坡的坡度i（即tanABC）为1：，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC（1）求出山坡坡角（A
8、BC）的大小；（2）求A、B两点间的距离（结果精确到0.1米，参考数据：1.732）25（1）如图1，AD、BC相交于点O，OAOC，OBDODB求证：ABCD（2）如图2，AB是O的直径，OA1，AC是O的弦，过点C的切线交AB的延长线于点D，若OD，求BAC的度数26小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元调研发现：盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；花卉的平均每盆利润始终不变小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完
9、后的利润分别为W1，W2（单位：元）（1）用含x的代数式分别表示W1，W2；（2）当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少？27设抛物线ymx22mx+3（m0）与x轴交于点A（a，0）和B（b，0）（1）若a1，求m，b的值；（2）若2m+n3，求证：抛物线的顶点在直线ymx+n上；（3）抛物线上有两点P（x1，p）和Q（x2，q），若x11x2，且x1+x22，试比较p与q的大小28平面直角坐标系中，二次函数y+bx+c的图象与坐标轴交于A，B，C三点，其中点A（3，0），点B（4，0），连接AC，BC，动点P从点C出发，在线段AC上以每秒1个单位长度
10、的速度向点A作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒连接PQ（1）求出二次函数的函数关系式；（2）在PQ的运动过程中，是否存在某一时刻t，使以AQ为直径的圆过点P？若存在，请求出运动时间t；若不存在，请说明理由；（3）求当t为何值时，APQ中有一个内角等于45？参考答案与试题解析一选择题（共11小题）1【分析】首先根据有理数大小比较的方法，判断出绝对值小于4的所有整数有哪些；然后把它们相加即可【解答】解：绝对值小于4的所有整数有：3、2、1、0、1、2、3，它们的和是：（3）+（2）+（
11、1）+0+1+2+30故选：C【点评】此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正数都大于0；负数都小于0；正数大于一切负数；两个负数，绝对值大的其值反而小2【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当原数绝对值1时，n是正数；当原数的绝对值1时，n是负数【解答】解：5100000005.1108，故选：B【点评】此题考查科学记数法的表示方法科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数，表示时关键要正确确定a的值以及n的值3【分析
12、】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形据此对图中的图形进行判断【解答】解：图（1）有一条对称轴，是轴对称图形，符合题意；图（2）不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义不符合题意；图（3）有二条对称轴，是轴对称图形，符合题意；图（3）有五条对称轴，是轴对称图形，符合题意；图（3）有一条对称轴，是轴对称图形，符合题意故轴对称图形有4个故选：C【点评】本题考查了轴对称图形的概念轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合4【分析】直接利用合并同类
13、项法则分别分析得出答案【解答】解：A、3a+2b，无法计算，故此选项错误；B、5a22a23a2，故此选项错误；C、7a+a8a，故此选项错误；D、2a2b4a2b2a2b，正确故选：D【点评】此题主要考查了合并同类项，正确掌握运算法则是解题关键5【分析】在运用三角形三边关系判定三条线段能否构成三角形时，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形【解答】解：A、7+89，能构成三角形；B、5+67，能构成三角形；C、3+45，能构成三角形；D、1+23，不能构成三角形故选：D【点评】本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，只要满足两短边
14、的和大于最长的边，就可以构成三角形6【分析】根据中位数、众数、方差、平均数的概念来解答【解答】解：平均数：甲组：（502+605+7010+8013+9014+1006）5080，乙组：（504+604+7016+802+9012+10012）5080，S甲2172S乙2256，故甲组学生成绩比乙组学生成绩稳定；甲组成绩的众数90乙组成绩的众数70；成绩80的人数甲组33人比乙组26人多；从中位数来看，甲组成绩80乙组成绩80，故错误成绩高于或等于90分的人数乙组24人比甲组20人多，高分段乙组成绩比甲组好故正确故选：C【点评】本题考查统计知识中的中位数和众数的定义将一组数据从小到大依次排列，
15、把中间数据（或中间两数据的平均数）叫做中位数一组数据中出现次数最多的数据叫做众数平均数是指在一组数据中所有数据之和再除以数据的个数它是反映数据集中趋势的一项指标样本方差描述了一组数据围绕平均数波动的大小7【分析】直接利用圆的面积公式求解【解答】解：SR2故选：B【点评】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）8【分析】因为骆驼的体温随时间的变化而变化，符合“对于一个变化过程中的两个量x和y，对于每一个x的值，y都有唯一的值和它相对应”的函数定义，自变量是时间，因变量是体温【解答】解：骆驼的体温随时间的变化而变化，自变量是时间，因变量是体温，故
16、选：B【点评】考查了函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数9【分析】根据图形翻折变换的性质可知，AEBE，设AEx，则BEx，CE8x，再在RtBCE中利用勾股定理即可求出BE的长度【解答】解：ADE翻折后与BDE完全重合，AEBE，设AEx，则BEx，CE8x，在RtBCE中（BE）2（BC）2+（CE）2，即x262+（8x）2，解得，x，BEx故选：A【点评】本题考查的是图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，
17、如本题中折叠前后角相等10【分析】应先求出上坡速度和下坡速度，注意往返路程上下坡路程的转化【解答】解：根据函数图象可得：明明骑自行车去上学时，上坡路为1千米，速度为16千米/分，下坡路程为312千米，速度为2（106）千米/分，放学后如果按原路返回，且往返过程中，上坡速度相同，下坡速度相同，那么他回来时，上坡路程为2千米，速度为千米/分，下坡路程为1千米，速度为千米/分，因此走这段路所用的时间为2+114分故选：D【点评】本题考查利用函数的图象解决实际问题11【分析】先解不等式得到x2，根据数轴表示数的方法得到解集在2的左边【解答】解：5+2x1，移项得2x4，系数化为1得x2故选：C【点评】
18、本题考查了在数轴上表示不等式的解集：先求出不等式组的解集，然后根据数轴表示数的方法把对应的未知数的取值范围通过画区间的方法表示出来，等号时用实心，不等时用空心二填空题（共7小题）12【分析】根据多边形的外角和等于360解答即可【解答】解：由多边形的外角和等于360可知，1+2+3+4+5360，故答案为：360【点评】本题考查的是多边形的内角和外角，掌握多边形的外角和等于360是解题的关键13【分析】等腰三角形ABC中a可能是底边，也可能是腰，应分两种情况进行讨论当a是腰时，则方程有一个根是3，代入即可求得m的值，从而求解；当a是底边时，方程有两个相等的实根，根据一元二次方程根的情况与判别式的
19、关系，从而求得其周长【解答】解：b、c是关于x的方程x2+mx+2m0的两个实数根，b+cm，bc2m分两种情况：当a为其腰时，则ba，或ca，方程必有一个根为3，代入方程得：9+3m+2m0，解得m，则b+c，则周长是a+b+c；当a为其底时，bc，原方程有两个相等的实数根，m24（2m）0，m14，m220（舍去），b+c4a，bc40，m4符合题意，a+b+c3+47ABC的周长为或7故答案为：或7【点评】本题考查了一元二次方程根的情况与判别式的关系，一元二次方程根与系数的关系，等腰三角形的性质及三角形的三边关系定理难度中等根据等腰三角形的性质，将a边进行分类是解题的关键一元二次方程ax
20、2+bx+c0（a0）的根与b24ac有如下关系：（1）0方程有两个不相等的实数根；（2）0方程有两个相等的实数根；（3）0方程没有实数根；一元二次方程根与系数的关系：如果x1，x2是一元二次方程ax2+bx+c0（a0）的两根，那么x1+x2，x1x2，反过来也成立，即（x1+x2），x1x2三角形的三边关系定理：两边之和大于第三边，两边之差小于第三边14【分析】根据直角三角形的性质求出AB，结合图形求出BD，根据射影定理计算【解答】解：ACB90，CE为AB边上的中线，AB2CE10，BDABAD8，由射影定理得，CD4，故答案为：4【点评】本题考查的是直角三角形的性质，射影定理，在直角三
21、角形中，斜边上的中线等于斜边的一半15【分析】根据题意归纳总结得到连续对折n次后，可以得到2n1条折痕，计算即可得到结果【解答】解：根据题意得：25132131，则连续对折5次后，可以得到31条折痕，故答案为：31【点评】此题考查了有理数的乘方，弄清折痕的规律是解本题的关键16【分析】先利用勾股定理计算出AB25，再利用面积法计算出CD12，接着证明CEFCAB，则可计算出EF25，同理可得从上往下数，第2个矩形的长为25，从上往下数，第（n1）个矩形的长为25，且所有矩形的宽的和为12，然后把所有矩形的面积相加即可【解答】解：如图，ACB90，AC15，BC20，AB25，CDABACBC，
22、CD12，斜边上的高CD分成n等分，CH，EFAB，CEFCAB，即，解得EF25，即从上往下数，第1个矩形的长为25，同理可得从上往下数，第2个矩形的长为25，从上往下数，第（n1）个矩形的长为25，而所有矩形的宽都为12，这（n1）张纸条的面积和是25+25+25 12（1+2+n1）12（cm2）故答案为【点评】本题考查了相似三角形的应用：从实际问题中抽象出几何图形，然后利用相似三角形的性质求解17【分析】由A，B为双曲线上的两点，利用反比例系数k的几何意义，求出矩形ACOG与矩形BEOF面积，再由阴影DGOF面积求出空白面积之和即可【解答】解：点A、B是双曲线y上的点，S矩形ACOGS
23、矩形BEOF6，S阴影DGOF2，S矩形ACDF+S矩形BDGE6+6228，故答案为：8【点评】此题考查了反比例函数系数k的几何意义，熟练掌握反比例函数系数k的几何意义是解本题的关键18【分析】（1）分别作出点A、B、C关于x轴的对称点，再首尾顺次连接即可得；（2）作点B关于y轴的对称点B，连接AB，与y轴的交点即为所求【解答】解：（1）如图所示，A1B1C1即为所求，由图知点C1的坐标（3，2），故答案为：（3，2）；（2）如图所示，点D即为所求，点D的坐标为（0，2）故答案为：（0，2）【点评】本题主要考查作图轴对称变换，解题的关键是掌握轴对称变换的定义和性质及轴对称最短路线问题三解答题
24、（共10小题）19【分析】根据题意可以求得x、y的值，从而可以求得xy的值【解答】解：x、y 是有理数，且 x，y 满足等式x2+2y+y174，解得，或，当x5，y4时，xy5（4）9，当x5，y4时，原式5（4）1【点评】本题考查实数，解答本题的关键是明确题意，求出相应的x、y的值20【分析】（1）原式化简后，合并同类二次根式得到最简结果，把x的值代入计算即可求出值；（2）原式括号中通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a与b的值代入计算即可求出值【解答】解：（1）原式3+，当x4时，原式7；（2）原式，当a1+，b1时，原式【点评】此题考查了分式的
25、化简求值，以及二次根式的化简求值，熟练掌握运算法则是解本题的关键21【分析】（1）用7次的人数除以7次所占的百分比即可求得总人数，然后求得6次的人数即可确定众数；（2）补齐6次小组的小长方形即可（2）用总人数乘以达标率即可【解答】解：（1）观察统计图知达到7次的有7人，占28%，728%25人，达到6次的有2525738人，故众数为6次；（4分）（2）（3）（人）答：该校125名九年级男生约有90人体能达标（3分）【点评】本题考查了条形统计图的知识，解题的关键是从统计图中整理出进一步解题的有关信息22【分析】（1）全班人数乘以选择“A高中”观点的百分比即可得到选择“A高中”观点的人数，用360
26、乘以选择“A高中”观点的百分比即可得到选择“A高中”的观点所在扇形区域的圆心角的度数；（2）用全校初三年级学生数乘以选择“B中技”观点的百分比即可估计该校初三学生选择“中技”观点的人数；（3）先计算出该班选择“就业”观点的人数为4人，则可判断有2位女同学和2位男生选择“就业”观点，再列表展示12种等可能的结果数，找出出现2女的结果数，然后根据概率公式求解【解答】解：（1）该班学生选择A高中观点的人数最多，共有60%5030（人），在扇形统计图中，该观点所在扇形区域的圆心角是60%360216；故答案为A高中（填A或高中等都可以），30，216；（2）80032%256（人），估计该校初三学生选
27、择“中技”观点的人数约是256人；（3）该班选择“就业”观点的人数50（160%32%）508%4（人），则该班有2位女同学和2位男生选择“就业”观点，列表如下：女1女2男1男2女1女2女1男1 女1男2女1女2女1女2男1女2男2女2男1女1男1女2男1男2男1男2女1男2女2男2男1男2共有12种等可能的结果数，其中出现2女的情况共有2种所以恰好选到2位女同学的概率【点评】本题考查了列表法或画树状图法：用列表法或画树状图法展示所有等可能的结果数n，再从中选出符合事件A或B的结果数目m，然后根据概率的公式求事件A和B的概率也考查根据样本估计总体和扇形统计图23【分析】由菱形的性质可证ACBD
28、，又已知EFAC，所以AGBG，GEBD，ADBC，可证四边形EDBF为平行四边形，可证GEGF，即证结论【解答】证明：连接BD，AF，BE，在菱形ABCD中，ACBDEFAC，EFBD，又EDFB，四边形EDBF是平行四边形，DEBF，E为AD的中点，AEED，AEBF，又AEBF，四边形AEBF为平行四边形，即AB与EF互相平分【点评】本题是简单的推理证明题，主要考查菱形的性质，同时综合利用平行四边形的判定方法及中位线的性质24【分析】（1）根据俯角以及坡度的定义即可求解；（2）在直角PHB中，根据三角函数即可求得PB的长，然后在直角PBA中利用三角函数即可求解【解答】解：（1）tanAB
29、C1：，ABC30；（2）由题意得：PBH60，ABC30，ABP90，又APB45，PAB为等腰直角三角形，在直角PHB中，PB20米在直角PBA中，ABPB2034.6米【点评】本题主要考查了解直角三角形的应用俯角的问题以及坡度的定义，正确利用三角函数是解题的关键25【分析】（1）由OBDODB，得出OBOD，再由SAS证得AOBCOD，即可得出结论；（2）连接OC，由CD与O相切，得出OCCD，求出CD1，得出OCD为等腰直角三角形，推出COD45，即可得出结果【解答】（1）证明：OBDODB，OBOD，在AOB与COD中，AOBCOD（SAS），ABCD；（2）解：连接OC，如图所示：
30、CD与O相切，OCCD，OAOC，OA1，OC1，CD1，CDOC，OCD为等腰直角三角形，COB45，BACCOB22.5【点评】本题主要考查了全等三角形的判定与性质、切线的性质、等腰直角三角形的判定与性质、圆周角定理等知识；熟练掌握全等三角形的判定与性质与圆周角定理是解决问题的关键26【分析】（1）设培植的盆景比第一期增加x盆，则第二期盆景有（50+x）盆，花卉有（50x）盆，根据“总利润盆数每盆的利润”可得函数解析式；（2）将盆景的利润加上花卉的利润可得总利润关于x的函数解析式，配方成顶点式，利用二次函数的性质求解可得【解答】解：（1）设培植的盆景比第一期增加x盆，则第二期盆景有（50+
31、x）盆，花卉有（50x）盆，所以W1（50+x）（1602x）2x2+60x+8000，W219（50x）19x+950；（2）根据题意，得：WW1+W22x2+60x+800019x+9502x2+41x+89502（x）2+，20，且x为整数，当x10时，W取得最大值，最大值为9160，答：当x10时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是9160元【点评】本题主要考查二次函数的应用，解题的关键是理解题意，找到题目蕴含的相等关系，据此列出函数解析式及二次函数的性质27【分析】（1）把（1，0）代入抛物线的解析式即可求出m的值，令y0代入抛物线的解析式即可求出点B的坐标
32、（2）易求抛物线的顶点坐标为（1，3m），把x1代入ymx+n中，判断y是否等于13m即可（3）根据x11x2，且x1+x22，可知P离对称轴较近，然后根据开口方向即可求出p与q的大小关系【解答】解：（1）当a1时，把（1，0）代入ymx22mx+3，解得m1，抛物线的解析式为：yx2+2x+3，令y0代入yx2+2x+3，x1或x3，b3，（2）抛物线的对称轴为：x1，把x1代入ymx22mx+3，y3m抛物线的顶点坐标为（1，3m），把x1代入ymx+n，ym+nm+32m3m顶点坐标在直线ymx+n上，（3）由题意可知：抛物线的对称轴为：x1，4m212m0，解得：m0或m3，x1+x2
33、2，x211x1，x11x2，|x21|x11|，P离对称轴较近，当m3时，pq，当m0时，pq，【点评】本题考查抛物线的综合问题，待定系数法求解析式，抛物线的对称轴方程，抛物线的图象与性质，本题属于中等题型28【分析】（1）设抛物线的表达式为：ya（x+3）（x4）（x2x12），即可求解；（2）由APQAOC，得，即可求解；（3）分AQP45、APQ45两种情况，求解即可【解答】解：（1）设抛物线的表达式为：ya（x+3）（x4）（x2x12）x2x4，（2）存在，理由：以AQ为直径的圆过点P，则APQ90，OACOAC，APQAOC，即：，解得t2；（3）由题意得：点C（0，4），OBOC，ABC45，当AQP45时，PQBC，AQPABC，解得：t；当APQ时，同理可得：t；由题意得：PAQ45，故：t或【点评】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似、圆的基本知识等，其中证明三角形相似是本题的主要考点
