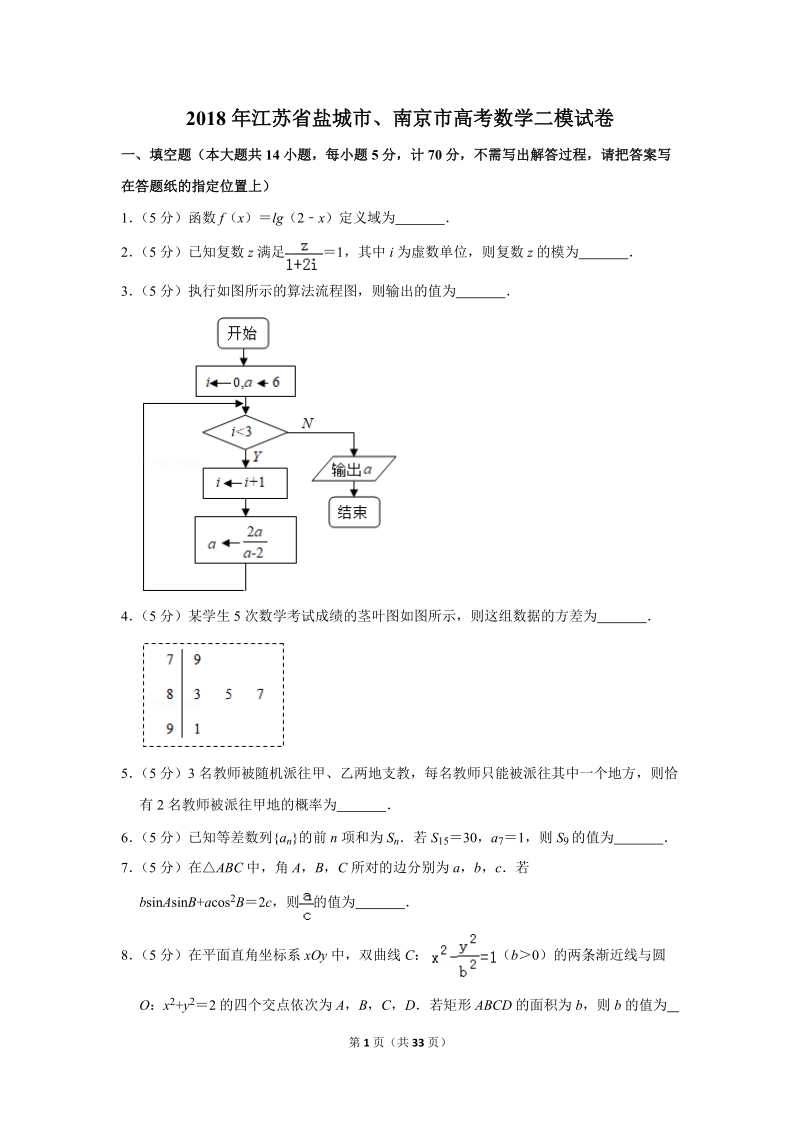
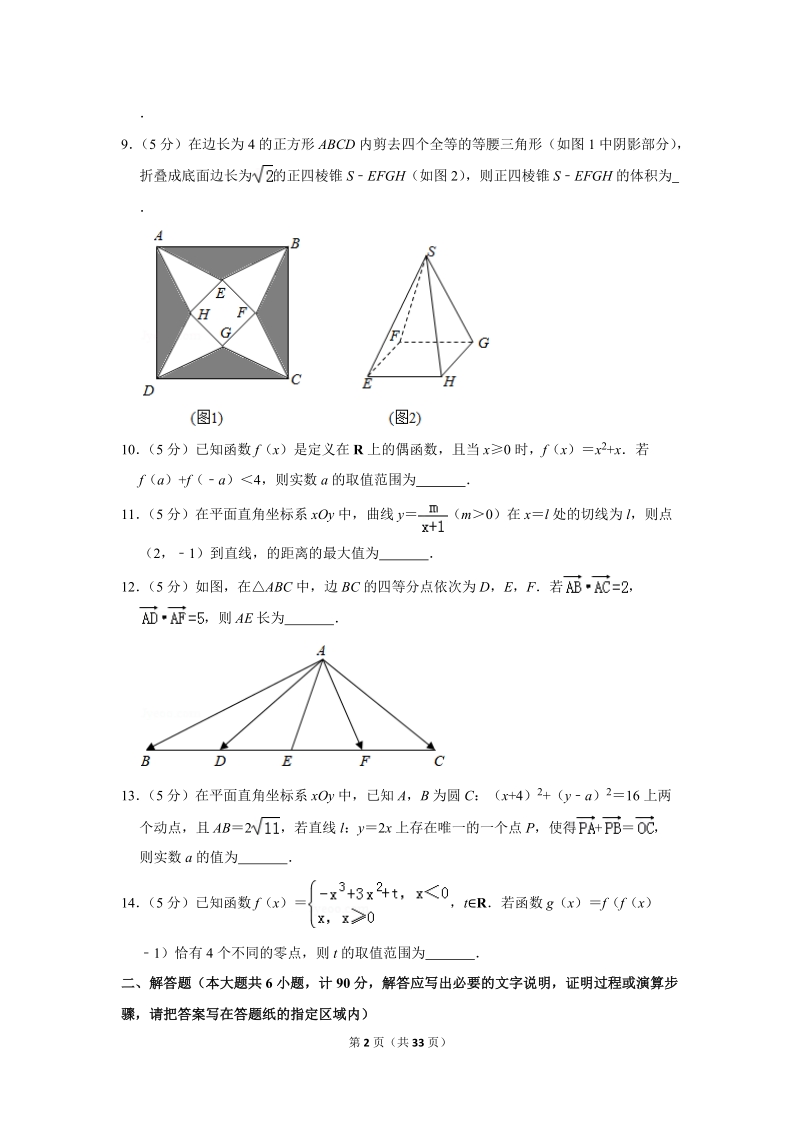
1、2018 年江苏省盐城市、南京市高考数学二模试卷一、填空题（本大题共 14 小题，每小题 5 分，计 70 分，不需写出解答过程，请把答案写在答题纸的指定位置上）1 （5 分）函数 f（x ）lg（2x）定义域为 2 （5 分）已知复数 z 满足 1，其中 i 为虚数单位，则复数 z 的模为 3 （5 分）执行如图所示的算法流程图，则输出的值为 4 （5 分）某学生 5 次数学考试成绩的茎叶图如图所示，则这组数据的方差为 5 （5 分）3 名教师被随机派往甲、乙两地支教，每名教师只能
2、被派往其中一个地方，则恰有 2 名教师被派往甲地的概率为 6 （5 分）已知等差数列a n的前 n 项和为 Sn若 S1530 ，a 71，则 S9 的值为 7 （5 分）在ABC 中，角 A，B，C 所对的边分别为 a，b，c若bsinAsinB+acos2B2c，则 的值为 8 （5 分）在平面直角坐标系 xOy 中，双曲线 C： （b0）的两条渐近线与圆O：x 2+y22 的四个交点依次为 A，B，C，D 若矩形 ABCD 的面积为 b，则 b 的值为 第 2 页（
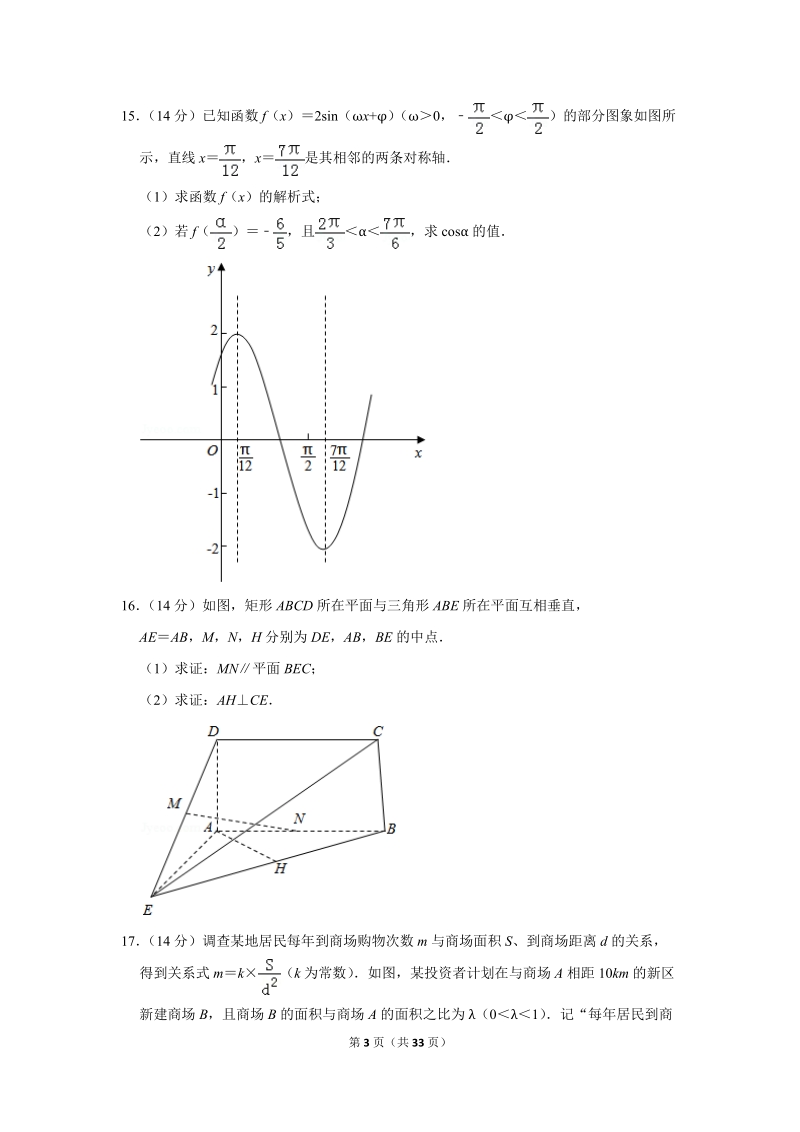
3、共 33 页）9 （5 分）在边长为 4 的正方形 ABCD 内剪去四个全等的等腰三角形（如图 1 中阴影部分） ，折叠成底面边长为 的正四棱锥 SEFGH（如图 2） ，则正四棱锥 SEFGH 的体积为 10 （5 分）已知函数 f（x ）是定义在 R 上的偶函数，且当 x0 时，f（x）x 2+x若f（a）+ f（a）4，则实数 a 的取值范围为 11 （5 分）在平面直角坐标系 xOy 中，曲线 y （m0）在 xl 处的切线为 l，则点（2，1）到直线，的距离的最大值为 12 （5 分）如图
4、，在ABC 中，边 BC 的四等分点依次为 D，E，F若 ，则 AE 长为 13 （5 分）在平面直角坐标系 xOy 中，已知 A，B 为圆 C：（x+4） 2+（y a） 216 上两个动点，且 AB2 ，若直线 l：y2x 上存在唯一的一个点 P，使得 + ，则实数 a 的值为 14 （5 分）已知函数 f（x ） ，t R若函数 g（x）f （f（x）1）恰有 4 个不同的零点，则 t 的取值范围为 二、解答题（本大题共 6 小题，计 90 分，解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答
5、题纸的指定区域内）第 3 页（共 33 页）15 （14 分）已知函数 f（x ）2sin（x+） （0， ）的部分图象如图所示，直线 x ，x 是其相邻的两条对称轴（1）求函数 f（x ）的解析式；（2）若 f（ ） ，且 ，求 cos 的值16 （14 分）如图，矩形 ABCD 所在平面与三角形 ABE 所在平面互相垂直，AE AB，M，N，H 分别为 DE，AB，BE 的中点（1）求证：MN平面 BEC；（2）求证：AHCE17 （14 分）调查某地居民每年到商场购物次数 m 与商场面积 S、到商场距离 d 的关系，得到关系式 mk （ k 为常数） 如图，某投资者计划在与商场 A 相距
6、 10km 的新区新建商场 B，且商场 B 的面积与商场 A 的面积之比为 （0 1） 记“每年居民到商第 4 页（共 33 页）场 A 购物的次数” 、 “每年居民到商场 B 购物的次数”分别为 m1、m 2，称满足 mlm 2 的区域叫做商场 B 相对于 A 的“更强吸引区域” （1）已知 P 与 A 相距 15km，且PAB60当 时，居住在 P 点处的居民是否在商场 B 相对于 A 的“更强吸引区域”内？，请说明理由；（2）若要使与商场 B 相距 2km 以内的区域（含边界）均为商场 B 相对于 A 的“更强吸引区域” ，求 的取值范围18 （16 分）如图，在平面直角坐标系 xOy
7、中，椭圆 E： + 1（ab0）的离心率为 ，上顶点 A 到右焦点的距离为 过点 D（0， m） （m0）作不垂直于 x 轴，y轴的直线，交椭圆 E 于 P，Q 两点，C 为线段 PQ 的中点，且 ACOC（1）求椭圆 E 的方程；（2）求实数 m 的取值范围；（3）延长 AC 交椭圆 E 于点 B，记AOB 与AOC 的面积分别为 S1，S 2，若 ，求直线 l 的方程19 （16 分）已知函数 f（x ）x（e x2） ，g（x）xlnx+k，kR，其中 e 为自然对数的底数记函数 F（x）f（x）+g（x） （1）求函数 yf（x）+2x 的极小值；（2）若 F（x） 0 的解集为（0，
8、+） ，求 k 的取值范围；（3）记 F（x）的极值点为 m，求证：函数 G（x ）|F（ x）|+ lnx 在区间（0，m ）上单第 5 页（共 33 页）调递增 （极值点是指函数取极值时对应的自变量的值）20 （16 分）对于数列a n，定义 bn（k）a n+an+k，其中 n，kN*（1）若 bn（2）b n（1）1，n N*，求 bn（4）b n（1）的值；（2）若 al2，且对任意的 n，k N*，都有 bn+1（k ）2b n（k） （i）求数列a n的通项公式；（ii）设 k 为给定的正整数，记集合 Ab n（k）|n N*，B5b n（k+2）|nN*，求证：AB 【选做题】
9、在 A、B、C、D 四小题中只能选做 2 题，每小题 0 分，共计 20 分，请在答题纸指定区域内作答解答应写出文字说明、证明过程或演算步骤选修 4-1：几何证明选讲21如图，AB 是圆 D 的直径， AC 是弦，BAC 的平分线 AD 交圆 D 于点 D，DEAC 且交 AC 的延长线于点 E，求证： DE 是圆 D 的切线选修 4-2：矩阵与变换22已知 a 为矩阵 A 属于实数 的一个特征向量，求 和 A2选修 4-4：坐标系与参数方程23在平面直角坐标系中，直线 l 的参数方程为 （t 为参数） ，圆 C 的参数方程为 （a0， 为参数） ，点 P 是圆 C 上的任意一点，
10、若点 P 到直线 l 距离的最大值为 3，求 a 的值，选修 4-5：不等式选讲24对任意 x，y R，求|xl |+|x|+|y1|+|y +1|的最小值，【必做题】第 22 题、第 23 题，每题 10 分，共 20 分，请在答题卡指定区域内作答，解答应写出文字说明、证明过程或演算步骤25甲，乙两人站在 P 点处分别向 A，B，C 三个目标进行射击，每人向兰个目标各射击一第 6 页（共 33 页）次，每人每次射击每个目标均相互独立，且两人各自击中 A，B，C 的概率分别都为 ， （1）设 X 表示甲击中目标的个数，求随机变量 X 的分布列和数学期望；（2）求甲乙两人共击中目标数为 2 个的
11、概率26已知 nN*，且 n4，数列 T：a 1，a 2，a n 中的每一项均在集合 Ml，2，n中，且任意两项不相等（1）若 n7，且 a2a 3a 4a 5a 6，求数列 T 的个数；（2）若数列 T 中存在唯一的 ak（k N*，且 kn） ，满足 aka k+1，求所有符合条件的数列 T 的个数第 7 页（共 33 页）2018 年江苏省盐城市、南京市高考数学二模试卷参考答案与试题解析一、填空题（本大题共 14 小题，每小题 5 分，计 70 分，不需写出解答过程，请把答案写在答题纸的指定位置上）1 （5 分）函数 f（x ）lg（2x）定义域为 （，2） 【分析】直接利用对数的真数大
12、于 0，求解即可【解答】解：要使函数有意义，可得 2x0，即 x2函数 f（x）lg（2x ）定义域为：（ ，2） 故答案为：（，2） 【点评】本题考查函数的定义域的求法，是基础题2 （5 分）已知复数 z 满足 1，其中 i 为虚数单位，则复数 z 的模为 【分析】利用复数代数形式的乘除运算化简，再由复数求模公式计算得答案【解答】解：由 1，得 z1+2 i则 故答案为： 【点评】本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题3 （5 分）执行如图所示的算法流程图，则输出的值为 3 【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出
13、变量 a 的第 8 页（共 33 页）值，模拟程序的运行过程，可得答案【解答】解：当 i0 时，满足继续循环的条件， i1，a 3，当 i1 时，满足继续循环的条件， i2，a6，当 i2 时，满足继续循环的条件， i3，a3，当 i3 时，不满足继续循环的条件，故输出的 a 值为 3，故答案为：3【点评】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答4 （5 分）某学生 5 次数学考试成绩的茎叶图如图所示，则这组数据的方差为 16 【分析】由茎叶图知该学生的 5 次考试成绩，计算平均数和方差即可【解答】解：由茎叶图知，该学生 5 次考试成绩是 79、83、
14、85、87、91；计算平均数为 （79+83+85+87）85，方差为 s2 （7985） 2+（8385） 2+（8585） 2+（8785） 2+（9185） 216故答案为：16【点评】本题考查了利用茎叶图中的数据计算平均数与方差的应用问题，是基础题5 （5 分）3 名教师被随机派往甲、乙两地支教，每名教师只能被派往其中一个地方，则恰有 2 名教师被派往甲地的概率为 【分析】基本事件总数 n2228，恰有 2 名教师被派往甲地包含的基本事件个数m 3，由此能求出恰有 2 名教师被派往甲地的概率【解答】解：3 名教师被随机派往甲、乙两地支教，每名教师只能被派往其中
15、一个地方，基本事件总数 n2228，第 9 页（共 33 页）恰有 2 名教师被派往甲地包含的基本事件个数 m 3，恰有 2 名教师被派往甲地的概率为 p 故答案为： 【点评】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，考查函数与方程思想，是基础题6 （5 分）已知等差数列a n的前 n 项和为 Sn若 S1530 ，a 71，则 S9 的值为 9 【分析】根据题意，由等差数列的前 n 项和公式可得 S15 15a 830，解可得 a8 的值，进而计算可得公差 d 的值，结合等差数列的通项公式可得a1a 76d5，进而由等差数列的前 n 项和公式可得 S99a 1+
16、 d，计算即可得答案【解答】解：根据题意，等差数列a n中，S 1530，则有 15a 830，解可得：a 82，则公差 da 8a 71，则 a1a 76d5，则 S99a 1+ d9；故答案为：9【点评】本题考查等差数列的性质以及应用，注意结合等差数列的性质求出公差7 （5 分）在ABC 中，角 A，B，C 所对的边分别为 a，b，c若bsinAsinB+acos2B2c，则 的值为 2 【分析】根据正弦定理，结合题意即可求出 的值【解答】解：ABC 中，bsinAsinB +acos2B2c，sinBsinAsin B+sinAcos2B2sinC；sinA2sinC， 2故答案为：2【
17、点评】本题考查了解三角形的应用问题，是基础题第 10 页（共 33 页）8 （5 分）在平面直角坐标系 xOy 中，双曲线 C： （b0）的两条渐近线与圆O：x 2+y22 的四个交点依次为 A，B，C，D 若矩形 ABCD 的面积为 b，则 b 的值为 【分析】根据双曲线 C： （b0）的两条渐近线方程为 ybx，联立方程组可得 ，求出点 A，B 的坐标，再根据矩形 ABCD 的面积为 b，即可求出【解答】解：双曲线 C： （b0）的两条渐近线方程为 ybx，联立方程组可得 ，解得 或 ，|AD | ，| AB| ，矩形 ABCD 的面积为 b， b解得 b27，b故答案为：第 11 页（共
18、 33 页）【点评】本题考查了双曲线的简单性质，以及直线和圆的交点问题，考查了运算能力，属于中档题9 （5 分）在边长为 4 的正方形 ABCD 内剪去四个全等的等腰三角形（如图 1 中阴影部分） ，折叠成底面边长为 的正四棱锥 SEFGH（如图 2） ，则正四棱锥 SEFGH 的体积为 【分析】连结 EG、FH，交于点 O，连结 SO，由题意 EHGF 是边长为 的正方形，SESFSG SH ，从而 EO1，SO 2，由此能求出正四棱锥SEFGH 的体积【解答】解：连结 EG、FH，交于点 O，连结 SO，由题意 EHGF 是边长为 的正方形，SESFSG SH ，EO 1，SO 2，正四棱
19、锥 SEFGH 的体积：第 12 页（共 33 页）V 故答案为： 【点评】本题考查四棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题10 （5 分）已知函数 f（x ）是定义在 R 上的偶函数，且当 x0 时，f（x）x 2+x若f（a）+ f（a）4，则实数 a 的取值范围为 （1，1） 【分析】根据 f（x ）为 R 上的偶函数，以及 x0 时 f（x）的解析式，便可讨论 a0 和a0，分别求出 f（a）+f（a） ，即可得出关于 a 的不等式，解不等式即得实数 a 的取值范围【解答】解：f（x ）是 R 上的偶函数，且
20、x0 时，f （x）x 2+x；a 0 时， f（a）+f（a）2f （a）2（a 2+a）4；整理得，a 2+a20；解得2a1；0a1；a0 时，f（a）+f（a）2f （a）2（a 2a）4；整理得，a 2a20；解得1a2；1a0；综上得，实数 a 的取值范围为（1，1） 故答案为：（1，1） 【点评】考查偶函数的定义，以及一元二次不等式的解法11 （5 分）在平面直角坐标系 xOy 中，曲线 y （m0）在 xl 处的切线为 l，则点（2，1）到直线，的距离的最大值为 第 13 页（共 33 页）【分析】求得函数 y 的导数，可得切线的斜率和切点，可得切线方
21、程，方法一、考虑切线恒过定点，可得定点和已知点的距离为最大值；方法二、运用点到直线的距离公式和基本不等式，可得最大值【解答】解：y （m 0）的导数为 y ，可得 x1 处切线的斜率为 k ，且切点为（1， ） ，可得切线 l 的方程为 y （x1） ，即为 mx+4y3m0，解法一、由于切线方程为 m（ x3）+4y0，可得切线恒过定点 P（3，0） ，点（2，1）到直线 l 的距离的最大值即为： ，解法二、点（2，1）到直线 l 的距离为：d ，当且仅当 m4 时，取得最大值 ，故答案为： 【点评】本题考查导数的运用：求切线方程，考查点到直线的距离公式的运用，以及基本不等式的运用，考查运算
22、能力，属于中档题12 （5 分）如图，在ABC 中，边 BC 的四等分点依次为 D，E，F若 ，则 AE 长为 【分析】用 和 表示出 得出 + + +6再根据第 14 页（共 33 页）的关系计算 + ，从而得出 AE 长【解答】解： 2 ， 2 ， ， + +2 + +2 ， + + +6 ， ， + 2 ， + 2 ， + 44 +4 40， + +644 +4 40， + 14，4 + +2 14+10 24，AE 故答案为： 【点评】本题考查了平面向量的基本定理和数量积运算，属于中档题13 （5 分）在平面直角坐标系 xOy 中，已知 A，B 为圆 C：（x
23、+4） 2+（y a） 216 上两个动点，且 AB2 ，若直线 l：y2x 上存在唯一的一个点 P，使得 + ，则实数 a 的值为 2 或18 【分析】设 A（x 1，y 1） ，B（ x2，y 2） ，圆 C：（x+4） 2+（ya） 216 的圆心C（4，a） ，半径 r4，求出圆心 C（4，a）到 AB 的距离为 ，设 P（x ，2x） ，则（x 1x，y 12 x）+（x 2x，y 22x ）（4，a） ，AB 中点 M（x2，2x + ） ，|CM| ，从而 5x2+（42a）x+ ，由直线 l：y2x上存在唯一的一个点 P，使得 + ， 0，由此能求出 a【解答】解：设 A（x
24、1，y 1） ， B（x 2，y 2） ，AB 的中点 M（ ， ） ，第 15 页（共 33 页）圆 C：（x+4） 2+（y a） 2 16 的圆心 C（4，a） ，半径 r4，圆心 C（4，a）到 AB 的距离|CM| ，直线 l：y2x 上存在唯一的一个点 P，使得 + ，设 P（x ，2x） ，则（x 1x，y 12x ）+ （x 2x，y 22x）（4，a） ， ， ，M（x2， 2x+ ） ，|CM | ，整理，得 5x2+（42a）x + ，直线 l：y2 x 上存在唯一的一个点 P，使得 + ， 0，整理，得 a2+16a360，解得 a2 或 a18【点评】本题考查实数值的
25、求法，考查点到直线的距离公式、直线与圆相切、中点坐标公式等基础知识，考查运用求解能力，考查函数与方程思想，是中档题14 （5 分）已知函数 f（x ） ，t R若函数 g（x）f （f（x）1）恰有 4 个不同的零点，则 t 的取值范围为 4，0） 【分析】若函数 g（x）f（f（x）1）恰有 4 个不同的零点，令 mf（x） ，即有f（m1）0，讨论 m1 或 s（0s1） ，由 s0，求得 t，结合图象进而得到答案【解答】解：函数 f（x ） ，当 x0 时，f（ x）x 3+3x2+t 的导数为f（x）3 x2+6x 在 x0 恒成立，可得 f（x）在 x0 递减，可令 g（x）f（f（
26、x ）1） 0，再令 mf（x） ，即有 f（m1）0，当 t0 时，f（m1）0，只有 m1，g（x）0 只有两解；第 16 页（共 33 页）当 t0 时，f（m1）0 有两解，可得 m1 或 s（0s1） ，由 f（x）1 和 f（x ）s 有两解，共 4 解，当 s0 时，m0，由x 3+3x2+t0，即有 f（1）0，解得 t4，可得 t 的范围是4，0） 故答案为：4，0） 【点评】本题考查函数的零点个数的解法，注意运用换元法和数形结合思想方法，考查运算能力，属于中档题二、解答题（本大题共 6 小题，计 90 分，解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指
27、定区域内）15 （14 分）已知函数 f（x ）2sin（x+） （0， ）的部分图象如图所示，直线 x ，x 是其相邻的两条对称轴（1）求函数 f（x ）的解析式；（2）若 f（ ） ，且 ，求 cos 的值第 17 页（共 33 页）【分析】 （1）由函数 f（x ）的部分图象，求得 T、 和 的值，写出函数 f（x）的解析式；（2）根据题意，利用三角恒等变换和同角的三角函数关系，即可求得 cos 的值【解答】解：（1）由函数 f（ x）2sin（x+）的部分图象知，T（ ）2 ， 2；又 x 时，f（x）取得最大值 2，2 + +2k，kZ； +2k，kZ；又 ，解得 ；函数 f（x）
28、2sin（2x + ） ；（2）若 f（ ） ，sin（+ ） ；又 ，+ ，第 18 页（共 33 页）cos（+ ） ；coscos（+ ） cos（+ ）cos +sin（+ ）sin +（ ） 【点评】本题考查了三角函数的图象与性质的应用问题，也考查了三角函数求值的应用问题，是综合题16 （14 分）如图，矩形 ABCD 所在平面与三角形 ABE 所在平面互相垂直，AE AB，M，N，H 分别为 DE，AB，BE 的中点（1）求证：MN平面 BEC；（2）求证：AHCE【分析】 （1）取 CD 中点 F，连结 NF、MF 推导出 NF BC，MFCE，从而平面BCE平面 MNF，由此能
29、证明 MN平面 BEC（2）推导出 AHBE ，BC平面 ABE，BCAH ，由此能证明 AH平面 BCE，从而AHCE【解答】证明：（1）取 CD 中点 F，连结 NF、MF ，矩形 ABCD 所在平面与三角形 ABE 所在平面互相垂直，M，N，H 分别为 DE，AB ， BE 的中点NFBC，MFCE，NFMFF，BCCEC，NF、MF 平面 MNF，BC、CE平面 BCE，第 19 页（共 33 页）平面 BCE平面 MNF，MN平面 MNF，MN平面 BEC（2）AEAB，H 为 BE 的中点，AHBE矩形 ABCD 所在平面与三角形 ABE 所在平面互相垂直，BC平面 ABE，BCA
30、H ，BEBCB，AH平面 BCE，AHCE【点评】本题考查线面平行、线线垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查函数与方程思想，考查函数与方程思想，是中档题17 （14 分）调查某地居民每年到商场购物次数 m 与商场面积 S、到商场距离 d 的关系，得到关系式 mk （ k 为常数） 如图，某投资者计划在与商场 A 相距 10km 的新区新建商场 B，且商场 B 的面积与商场 A 的面积之比为 （0 1） 记“每年居民到商场 A 购物的次数 ”、 “每年居民到商场 B 购物的次数”分别为 m1、m 2，称满足 mlm 2 的区域叫做商场 B 相对于 A 的“更强吸引
31、区域” （1）已知 P 与 A 相距 15km，且PAB60当 时，居住在 P 点处的居民是否在商场 B 相对于 A 的“更强吸引区域”内？，请说明理由；（2）若要使与商场 B 相距 2km 以内的区域（含边界）均为商场 B 相对于 A 的“更强吸引区域” ，求 的取值范围第 20 页（共 33 页）【分析】 （1）设商场 A，B 的面积分别为 S1，S 2，点 P 到 A，B 的距离分别为 d1，d 2 则S2S 1， ， ，k 为常数，k0，由余弦定理得 PB 2175.PA 2225，m 1m 2 kS 1（ ） ，由此能求出当 时，居住在 P 点处的居民是不在商场 B 相对于 A 的“
32、更强吸引区域”内（2）以 AB 所在直线为 x 轴，A 为原点，建立平面直角坐标系，由 m1m 2，得 ，将 S2S 1 代入，得 ，从而（1 ）x 2+（1）y220x+100 0，推导出商场 B 相对于 A 的“更强吸引区是：圆心为 C（ ，0） ，半径为 r1 的圆的内部，由此能求出 的取值范围【解答】解：（1）设商场 A，B 的面积分别为 S1，S 2，点 P 到 A，B 的距离分别为d1，d 2，则 S2S 1， ， ，k 为常数，k0 ，在PAB 中，AB10，PA15，PAB60，由余弦定理得：PB 2AB 2+PA22AB PAcos6010 2+1522 175又 PA 22
33、25，此时，m 1m 2 kS1（ ） ，将 代入，得 m1m 2kS 1（ ） ，kS 10，m 1m 2，当 时，居住在 P 点处的居民是不在商场 B 相对于 A 的“更强吸引区域”内（2）以 AB 所在直线为 x 轴，A 为原点，建立如图所示的平面直角坐标系，第 21 页（共 33 页）由 m1m 2，得 ，将 S2S 1 代入，得 ，代入坐标，得（x10） 2+y2（x 2+y2） ，化简，得（1）x 2+（1）y 220x+1000，01，配方得（x ） 2+y2（ ） 2，商场 B 相对于 A 的“更强吸引区是：圆心为 C（ ，0） ，半径为 r1 的圆的内部，与商场 B 相距 2
34、km 的区域（含边界）是：圆心为 B（10， 0） ，半径为 r22 的圆的内部及圆周，由题设，圆 B 内含于圆 C，即 BC|r 1r 2|，01， 10 2，解得 的取值范围是（ ） 【点评】本题考查函数在生产生活中的实际运用，考查函数、圆的性质，考查推理论证能力、运算求解能力，考查函数与方程思想，是中档题18 （16 分）如图，在平面直角坐标系 xOy 中，椭圆 E： + 1（ab0）的离心率为 ，上顶点 A 到右焦点的距离为 过点 D（0， m） （m0）作不垂直于 x 轴，y轴的直线，交椭圆 E 于 P，Q 两点，C 为线段 PQ 的中点，且 ACOC（1）求椭圆 E 的方程；（2）
35、求实数 m 的取值范围；第 22 页（共 33 页）（3）延长 AC 交椭圆 E 于点 B，记AOB 与AOC 的面积分别为 S1，S 2，若 ，求直线 l 的方程【分析】 （1）根据椭圆的性质即可求得 a 和 b 的值，即可求得椭圆方程；方法一：（2）利用点差法及直线垂直的关系，即可求得 y02m1，x 02（12m ）（2m2）0，即可求得 m 的取值范围；（3）设 B 点坐标，代入椭圆方程，根据直线的斜率公式即可求得 x3 ，根据三角形的面积公式，即可求得 m 的值，求得直线 AB 的方程；方法二：（2）设直线 l 的方程，代入椭圆方程，利用韦达定理，中点坐标公式及直线的斜率公式求得 m
36、，化简即可求得 m 的取值范围；（3）求得直线 AB 的方程，代入椭圆方程，即可求得 B 点坐标，根据三角形的面积公式，即可求得 k 及 m 的值，即可求得直线 l 的方程【解答】解：（1）由椭圆的离心率 e ，则 a c，由上顶点 A 到右焦点的距离为 ，即 a ，则 bc1，椭圆的标准方程： ；解法一：（2）由 A（0，1） ，设 P（x 1，y 1） ，Q （x 2，y 2） ，C（x 0，y 0） ，且 x1x 2，由 P，Q 在椭圆上，x 12+2y122， x22+2y222， 2x0x 1+x2，2y 0y 1+y2，两式相减得： ，由 ，则 ，整理得：x 022y 0（m y
37、0） ，第 23 页（共 33 页）由 ACOC，则 1，整理得：x 02y 0（1y 0） ，由解得： y02m1，x 02（12m ） （2m 2）0 ，解得： m1，m 的取值范围：（ ，1） ；（3）设 B（x 3，y 3） ，由 B 在椭圆 E 上，x 32+2y322，由 ACOC，则 1，即 y3 x3+1，代入上式消去 y3，得 x3 ，所以 | |，由（2）可知：y 02m 1，x 02（12m） （2m2）0， m1， | | | ，由 ，即 ，解得：m ，此时 y02m1 ，x 02（12m） （2m2） ，解得：x 0 ，此时 C 点坐标为（ ， ） ，D（0， ） ，
38、直线方程为 y x+ 或 y x+ 方法二：（2）由（1）可得 A（0，1） ，设 P（x 1，y 1） ，Q（x 2，y 2） ，C（x 0，y 0） ，设直线 l 方程为 ykx+m， （k0） ，代入椭圆方程：（1+2k 2）x 2+4kmx+2m220， （*）x1+x2 ，则 x0 ，第 24 页（共 33 页）y0kx 0+m ，C（ ， ） ，则 kAC ，由 kOC ，由 ACOC，则 kACkOC1，整理得：m ，由 k0，则 m 1 1 （ ，1） ，m 的取值范围（ ，1） ；（3）设 B（x 3，y 3） ，k AB 2k ，设直线 AB 的方程为 y2kx+1，与椭圆
39、方程联立，解得：x 或 x0（舍去） ，即 x3 ，x0 ，则 | | ，由 ，即 ，解得：k ，m ，则 D（0， ） ，直线方程为 y x+ 或 y x+ 【点评】本题考查椭圆的标准方程，直线与椭圆的位置关系，考查韦达定理，中点坐标第 25 页（共 33 页）公式及“点差法”的应用，考查转化思想，属于中档题19 （16 分）已知函数 f（x ）x（e x2） ，g（x）xlnx+k，kR，其中 e 为自然对数的底数记函数 F（x）f（x）+g（x） （1）求函数 yf（x）+2x 的极小值；（2）若 F（x） 0 的解集为（0，+） ，求 k 的取值范围；（3）记 F（x）的极值点为 m，
40、求证：函数 G（x ）|F（ x）|+ lnx 在区间（0，m ）上单调递增 （极值点是指函数取极值时对应的自变量的值）【分析】 （1）yf（x）+2xxe x，由 y（x+1）e x0 ，得 x1，利用职权利用导数能求出函数 yf（x）+2x 的极小值（2）F（x） f（x）+g（x）xe xxlnx+k，F（x ）（x+1） （e x ） ，设 h（x）e x ， （x0） ，则 0 恒成立，由此利用导数性质能求出 k 的取值范围（3）mx 0，当 1+k0，即 k1 时，F（x）0 恒成立，函数 G（x）在（0，m）上单调递增；当 1+k0，即 k1 时，0e k m，F（x ）在（0，
41、m）上存在唯一的零点 x1，函数 G（x）在（0，x 1上单调递增，当 x1xm 时，F（x ）0，G（x）F（x）+lnx，G（x）F（x）+ ，G（x）在 x1，m）上单调递增 设任意 s，t（0， m） ，且 st，总有 G（s） G（t ） ，由此能证明函数G（x）|F （x）|+lnx 在区间（0，m）上单调递增【解答】解：（1）函数 f（ x）x（e x2） ，yf （x）+2xxe x，y（x+1）e x，由 y0，得 x1，列表如下：x （，1） 1 （1，+）y 0 +y 极小值 当 x1 时，函数 yf（x）+2x 的极小值为
42、 （2）函数 f（x ）x（e x2） ，g（x）xlnx +k，kR，其中 e 为自然对数的底数记函数 F（x） f（x）+g（x） 第 26 页（共 33 页）F（x ）f（x）+g（x）xe xxlnx+k，F（x ）（x+1） （e x ） ，设 h（x）e x ， （x 0） ，则 0 恒成立，函数 h（x）在（0，+）上单调递增，又 h（ ） 20，h（1）e10，且 h（x）的图象在（0，+）上不间断，h（x）在（0，+）上存在唯一的零点 x0（ ，1） ，且 ，当 x（0，x 0）时，h（x）0，即 F（x ）0，当 x（x 0，+）时，h（x）0，即 F（x）0，F（x ）在
43、（0 ，x 0）上单调递减，在（ x0，+）上单调递增，xx 0 时，函数 F（x）取极小值（即最小值）为 F（x 0） x 0lnx 0+k1x 0ln +k1+k，F（x ）0 的解集为（ 0，+） ，1+k0，解得中，k 的取值范围是（1，+） 证明：（3）由（2）知 mx 0，当 1+k0，即 k1 时，F（x）0 恒成立，G（x）F（x）+lnxxe xx+k，G（x ）（x+1）e x1，x（0，m） ，x +11，e x1，G （x）0 恒成立，函数 G（x）在（0，m）上单调递增当 1+k0，即 k1 时，0e k m，F（e k）e k（e k1）0，F（m）F （x 0）1
44、+k0，又 F（x ）在（ 0，m）上单调递减，且图象不间断，F（x ）在（0 ，m）上存在唯一的零点 x1，当 0xx 1 时，F（x）0，G （x ）F（x）+lnxxe xx+k，G （x）（x+1）ex1，0xx 1，x +11，e x1，G （x）0 恒成立，函数 G（x）在（0，x 1上单调递增，第 27 页（共 33 页）当 x1xm 时，F（x ）0， G（x）F（x）+lnx，G（x ）F（x）+ ，由（2）知，当 x1x m 时，F（x）0，G（x）0 恒成立，G （x ）在 x1，m ）上单调递增设任意 s，t（0，m） ，且 s t，若 tx 1，则由 知 G（s）G（
45、t ） ，若 sx 1t，则由 知 G（s）G（x 1） ，由知 G（x 1） G（t ） ，G （s）G（t） 总有 G（s）G（t） ，G（x）在（0，m）上单调递增，综上，函数 G（x）| F（x ）|+ lnx 在区间（0，m）上单调递增【点评】本题考查函数的极小值的求法，考查实数的取值范围的求法，考查函数的单调性的证明，考查导数性质、构造法等基础知识，考查运算求解能力，考查函数与方程思想，是中档题20 （16 分）对于数列a n，定义 bn（k）a n+an+k，其中 n，kN*（1）若 bn（2）b n（1）1，n N*，求 bn（4）b n（1）的值；（2）若 al2，且对任意的 n，k N*，都有 bn+1（k ）2b n（k） （i）求数列a n的通项公式；（ii）设 k 为给定的正整数，记集合 Ab n（k）|n N*，B5b n（k+2）|nN*，求证：AB 【分析】 （1）推导出数列a n+1是公差为 1 的等差数列，由此能求出出 bn（4）b n（1） （2） （i）由 bn+1（k ）2b n（ k） ，a n+1+an+1+k2（a n+an+k） ，分别令 k1 及 k
