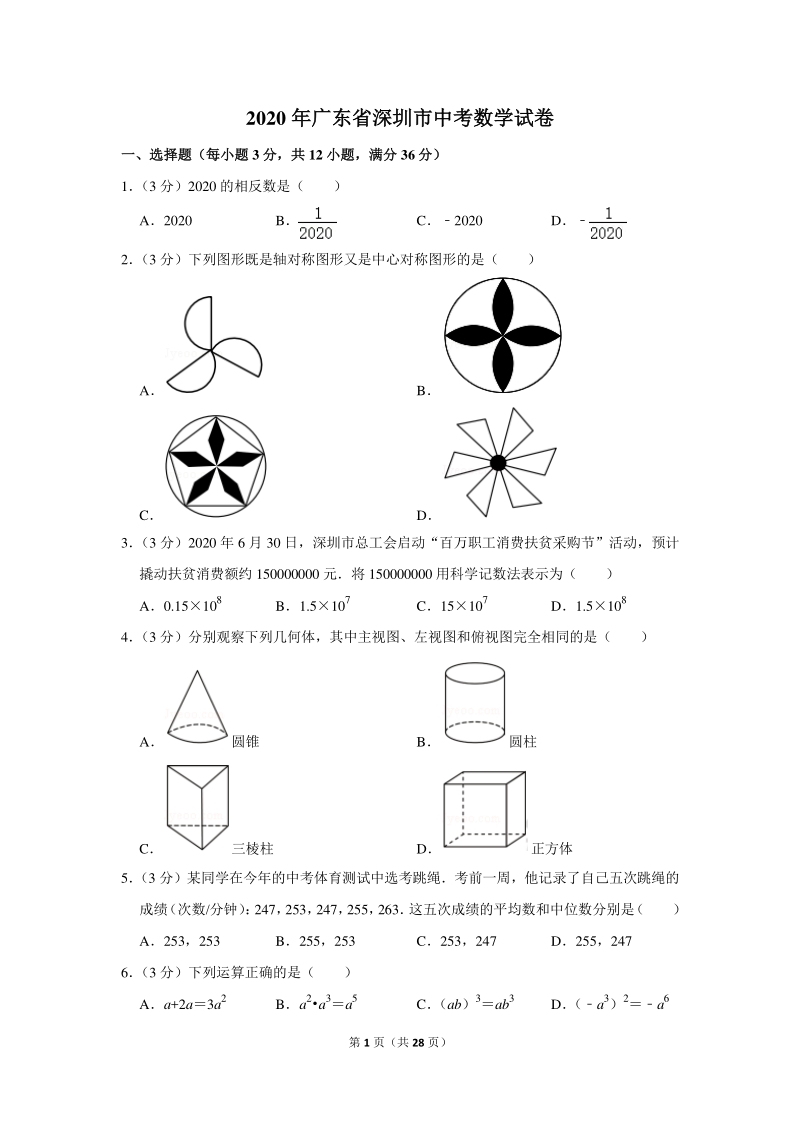
1、2020 年 6 月 30 日，深圳市总工会启动“百万职工消费扶贫采购节”活动，预计 撬动扶贫消费额约 150000000 元将 150000000 用科学记数法表示为（ ） A0.15108 B1.5107 C15107 D1.5108 4 （3 分）分别观察下列几何体，其中主视图、左视图和俯视图完全相同的是（ ） A圆锥 B圆柱 C三棱柱 D正方体 5 （3 分）某同学在今年的中考体育测试中选考跳绳考前一周，他记录了自己五次跳绳的 成绩 （次数/分钟） ： 247， 253， 247， 255， 263 这五次成绩的平均数和中位数
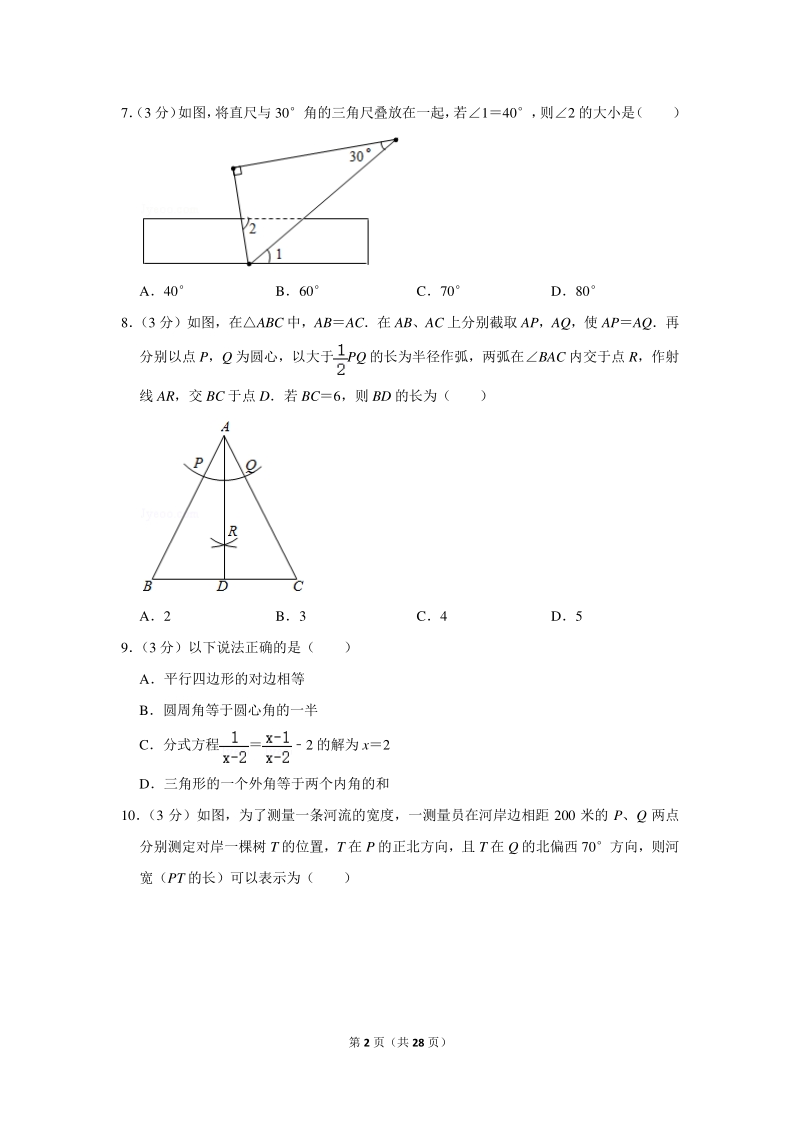
2、分别是 （ ） A253，253 B255，253 C253，247 D255，247 6 （3 分）下列运算正确的是（ ） Aa+2a3a2 Ba2a3a5 C （ab）3ab3 D （a3）2a6 第 2 页（共 28 页） 7（3 分） 如图， 将直尺与 30角的三角尺叠放在一起， 若140， 则2 的大小是 （ ） A40 B60 C70 D80 8 （3 分）如图，在ABC 中，ABAC在 AB、AC 上分别截取 AP，AQ，使 APAQ再 分别以点 P，Q 为圆心，以大
3、于PQ 的长为半径作弧，两弧在BAC 内交于点 R，作射 线 AR，交 BC 于点 D若 BC6，则 BD 的长为（ ） A2 B3 C4 D5 9 （3 分）以下说法正确的是（ ） A平行四边形的对边相等 B圆周角等于圆心角的一半 C分式方程2 的解为 x2 D三角形的一个外角等于两个内角的和 10 （3 分）如图，为了测量一条河流的宽度，一测量员在河岸边相距 200 米的 P、Q 两点 分别测定对岸一棵树 T 的位置，T 在 P 的正北方向，且 T 在 Q 的北偏西 70方向，则河 宽（PT 的长）可以表
4、示为（ ） 第 3 页（共 28 页） A200tan70米 B米 C200sin 70米 D米 11 （3 分） 二次函数 yax2+bx+c （a0） 的顶点坐标为 （1， n） ， 其部分图象如图所示 以 下结论错误的是（ ） Aabc0 B4acb20 C3a+c0 D关于 x 的方程 ax2+bx+cn+1 无实数根 12 （3 分）如图，矩形纸片 ABCD 中，AB6，BC12将纸片折叠，使点 B 落在边 AD 的延长线上的点 G 处，折痕为 E
5、F，点 E、F 分别在边 AD 和边 BC 上连接 BG，交 CD 于点 K，FG 交 CD 于点 H给出以下结论： EFBG； GEGF； GDK 和GKH 的面积相等； 当点 F 与点 C 重合时，DEF75， 其中正确的结论共有（ ） 第 4 页（共 28 页） A1 个 B2 个 C3 个 D4 个 二、填空题（本二、填空题（本题共题共 4 小题，每小题小题，每小题 3 分，共分，共 12 分）分） 13 （3 分）分解因式：m3m &n
6、bsp; 14 （3 分）一口袋内装有编号分别为 1，2，3，4，5，6，7 的七个球（除编号外都相同） ， 从中随机摸出一个球，则摸出编号为偶数的球的概率是 15 （3 分）如图，在平面直角坐标系中，O（0，0） ，A（3，1） ，B（1，2） 反比例函数 y （k0）的图象经过OABC 的顶点 C，则 k 16 （3 分）如图，在四边形 ABCD 中，AC 与 BD 相交于点 O，ABCDAC90，tan ACB，则 三、解答题（本题共三、解答题（本题共 7 小题，共小题，共 52
7、分）分） 第 5 页（共 28 页） 17 （5 分）计算： （） 12cos30+| |（4）0 18 （6 分）先化简，再求值：（2+） ，其中 a2 19 （7 分）以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业 态发展对人才的需求更加旺盛某大型科技公司上半年新招聘软件、硬件、总线、测试 四类专业的毕业生，现随机调查了 m 名新聘毕业生的专业情况，并将调查结果绘制成如 图两幅不完整的统计图 请根据统计图提供的信息，解答下列问题 （1）m ，n &nb
8、sp; （2）请补全条形统计图； （3）在扇形统计图中， “软件”所对应的扇形的圆心角是 度； （4）若该公司新招聘 600 名毕业生，请你估计“总线”专业的毕业生有 名 20 （8 分）如图，AB 为O 的直径，点 C 在O 上，AD 与过点 C 的切线互相垂直，垂足 为 D连接 BC 并延长，交 AD 的延长线于点 E （1）求证：AEAB； （2）若 AB10，BC6，求 CD 的长 21 （8 分）端午节前夕，某商铺用 620 元购进 50 个肉粽和 30 个蜜枣粽，肉粽的进货单价 &
9、nbsp; 第 6 页（共 28 页） 比蜜枣粽的进货单价多 6 元 （1）肉粽和蜜枣粽的进货单价分别是多少元？ （2）由于粽子畅销，商铺决定再购进这两种粽子共 300 个，其中肉粽数量不多于蜜枣粽 数量的 2 倍，且每种粽子的进货单价保持不变，若肉粽的销售单价为 14 元，蜜枣粽的销 售单价为 6 元， 试问第二批购进肉粽多少个时， 全部售完后， 第二批粽子获得利润最大？ 第二批粽子的最大利润是多少元？ 22 （9 分） 背景： 一次小组合作探究课上， 小明将两个正方形按如图所示的位置摆放 （点 E、 A、D 在同一条直线上） ，发现 BED
10、G 且 BEDG 小组讨论后，提出了下列三个问题，请你帮助解答： （1）将正方形 AEFG 绕点 A 按逆时针方向旋转（如图 1） ，还能得到 BEDG 吗？若能， 请给出证明；若不能，请说明理由； （2）把背景中的正方形分别改成菱形 AEFG 和菱形 ABCD，将菱形 AEFG 绕点 A 按顺时 针方向旋转（如图 2） ，试问当EAG 与BAD 的大小满足怎样的关系时，背景中的结论 BEDG 仍成立？请说明理由； （3）把背景中的正方形分别改写成矩形 AEFG 和矩形 ABCD，且，AE4， AB8，将矩形 AEFG 绕点 A 按顺时针方向旋转
11、（如图 3） ，连接 DE，BG小组发现： 在旋转过程中，DE2+BG2的值是定值，请求出这个定值 23 （9 分）如图 1，抛物线 yax2+bx+3（a0）与 x 轴的交点 A（3，0）和 B（1，0） ， 与 y 轴交于点 C，顶点为 D 第 7 页（共 28 页） （1）求该抛物线的解析式； （2）连接 AD，DC，CB，将OBC 沿 x 轴以每秒 1 个单位长度的速度向左平移，得到 OBC，点 O、B、C 的对应点分别为点 O、B、C，设平移时间为 t 秒，当点 O与点 A 重合时停止移动记OBC与四边形
12、 AOCD 重合部分的面积为 S，请直接写出 S 与 t 之 间的函数关系式； （3）如图 2，过该抛物线上任意一点 M（m，n）向直线 l：y作垂线，垂足为 E，试 问在该抛物线的对称轴上是否存在一点 F，使得 MEMF？若存在，请求出 F 的坐 标；若不存在，请说明理由 第 8 页（共 28 页） 2020 年广东省深圳市中考数学试卷年广东省深圳市中考数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（每小题一、选择题（每小题 3 分，共分，共 12 小题，满分小题，满分 36 分）分） &n
13、bsp;1 （3 分）2020 的相反数是（ ） A2020 B C2020 D 【分析】直接利用相反数的定义得出答案 【解答】解：2020 的相反数是：2020 故选：C 【点评】此题主要考查了相反数，正确把握相反数的定义是解题关键 2 （3 分）下列图形既是轴对称图形又是中心对称图形的是（ ） A B C D 【分析】根据中心对称图形与轴对称图形的概念进行判断即可 【解答】解：A、不是中心对称图形，不是轴对称图形，故此选项不合题意； B、既是中心对称图形，又是
14、轴对称图形，故此选项符合题意； C、不是中心对称图形，是轴对称图形，故此选项不合题意； D、是中心对称图形，不是轴对称图形，故此选项不合题意； 故选：B 【点评】本题考查的是中心对称图形与轴对称图形的概念轴对称图形的关键是寻找对 称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部 分重合 3 （3 分）2020 年 6 月 30 日，深圳市总工会启动“百万职工消费扶贫采购节”活动，预计 第 9 页（共 28 页） 撬动扶贫消费额约 150000000 元将 150000000
15、 用科学记数法表示为（ ） A0.15108 B1.5107 C15107 D1.5108 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数 【解答】解：将 150000000 用科学记数法表示为 1.5108 故选：D 【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n的形式，其 中 1|a|10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值 4 （3 分）分别观察下列几何体，其中主视图、左视图和俯视图完全相同的是（ ） A圆锥 B圆柱
16、C三棱柱 D正方体 【分析】分别得出圆锥体、圆柱体、三棱柱、正方体的三视图的形状，再判断即可 【解答】解：圆锥的主视图、左视图都是等腰三角形，而俯视图是圆，因此选项 A 不符 合题意； 圆柱体的主视图、左视图都是矩形，而俯视图是圆形，因此选项 B 不符合题意； 三棱柱主视图、左视图都是矩形，而俯视图是三角形，因此选项 C 不符合题意； 正方体的三视图都是形状、大小相同的正方形，因此选项 D 符合题意； 故选：D 【点评】本题考查简单几何体的三视图，明确圆锥、圆柱、三棱柱、正方体的三视图的 形状和大小是正确判断的
17、前提 5 （3 分）某同学在今年的中考体育测试中选考跳绳考前一周，他记录了自己五次跳绳的 成绩 （次数/分钟） ： 247， 253， 247， 255， 263 这五次成绩的平均数和中位数分别是 （ ） A253，253 B255，253 C253，247 D255，247 【分析】根据中位数、众数的计算方法，分别求出结果即可 【解答】解： （247+253+247+255+263）5253， 这 5 个数从小到大，处在中间位置的一个数是 253，因此中位数是 253； 第 10 页（共 28 页） &nb
18、sp; 故选：A 【点评】本题考查中位数、众数的意义和计算方法，掌握中位数、众数的计算方法是正 确计算的前提 6 （3 分）下列运算正确的是（ ） Aa+2a3a2 Ba2a3a5 C （ab）3ab3 D （a3）2a6 【分析】利用合并同类项、幂的乘方、积的乘方以及同底数幂的乘法的计算法则进行计 算即可 【解答】解：a+2a3a，因此选项 A 不符合题意； a2a3a2+3a5，因此选项 B 符合题意； （ab）3a3b3，因此选项 C 不符合题意； （a3）2a6，因此选项 D 不符合题意；
19、 故选：B 【点评】本题考查合并同类项、幂的乘方、积的乘方以及同底数幂的乘法的计算法则， 掌握计算法则是正确计算的前提 7（3 分） 如图， 将直尺与 30角的三角尺叠放在一起， 若140， 则2 的大小是 （ ） A40 B60 C70 D80 【分析】根据平角的定义和平行线的性质即可得到结论 【解答】解：由题意得，460， 140， 3180604080， ABCD， 3280， 故选：D 第 11 页（共 28 页） &
20、nbsp; 【点评】本题考查了平行线的性质，平角的定义，熟练掌握平行线的性质是解题的关键 8 （3 分）如图，在ABC 中，ABAC在 AB、AC 上分别截取 AP，AQ，使 APAQ再 分别以点 P，Q 为圆心，以大于PQ 的长为半径作弧，两弧在BAC 内交于点 R，作射 线 AR，交 BC 于点 D若 BC6，则 BD 的长为（ ） A2 B3 C4 D5 【分析】依据等腰三角形的性质，即可得到 BDBC，进而得出结论 【解答】解：由题可得，AR 平分BAC， 又ABAC， AD 是三角形 ABC 的中线
21、， BDBC63， 故选：B 【点评】本题主要考查了基本作图以及等腰三角形的性质，等腰三角形的顶角平分线、 底边上的中线、底边上的高相互重合 9 （3 分）以下说法正确的是（ ） A平行四边形的对边相等 B圆周角等于圆心角的一半 C分式方程2 的解为 x2 D三角形的一个外角等于两个内角的和 第 12 页（共 28 页） 【分析】根据平行四边形的性质对 A 进行判断；根据圆周角定理对 B 进行判断；利用分 式方程有检验可对 C 进行判断；根据三角形外角性质对
22、D 进行判断 【解答】解：A、平行四边形的对边相等，所以 A 选项正确； B、一条弧所对的圆周角等于它所对的圆心角的一半，所以 B 选项错误； C、去分母得 1x12（x2） ，解得 x2，经检验原方程无解，所以 C 选项错误； D、三角形的一个外角等于与它不相邻的两个内角的和，所以 D 选项错误 故选：A 【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都 等于这条弧所对的圆心角的一半 10 （3 分）如图，为了测量一条河流的宽度，一测量员在河岸边相距 200 米的 P、Q 两点 分
23、别测定对岸一棵树 T 的位置，T 在 P 的正北方向，且 T 在 Q 的北偏西 70方向，则河 宽（PT 的长）可以表示为（ ） A200tan70米 B米 C200sin 70米 D米 【分析】在直角三角形 PQT 中，利用 PQ 的长，以及PQT 的度数，进而得到PTQ 的 度数，根据三角函数即可求得 PT 的长 【解答】解：在 RtPQT 中， QPT90，PQT907020， PTQ70， tan70， PT， 即河宽米， 第 13 页（共 28 页）
24、 故选：B 【点评】此题考查了解直角三角形的应用方向角问题，掌握方向角与正切函数的定义 是解题的关键 11 （3 分） 二次函数 yax2+bx+c （a0） 的顶点坐标为 （1， n） ， 其部分图象如图所示 以 下结论错误的是（ ） Aabc0 B4acb20 C3a+c0 D关于 x 的方程 ax2+bx+cn+1 无实数根 【分析】根据抛物线开口方向，对称轴的位置以及与 y 轴的交点可以对 A 进行判断；根 据抛物线与 x 轴的交点情况可对 B 进行判断；x1 时，y0，可对 C 进行判
25、断；根据抛 物线 yax2+bx+c 与直线 yn+1 无交点，可对 D 进行判断 【解答】解：A抛物线开口向下， a0， 对称轴为直线 x1， b2a0， 抛物线与 y 轴交于正半轴， c0， abc0， 故 A 正确； B抛物线与 x 轴有两个交点， b24ac0，即 4acb20， 故 B 正确； C抛物线的对称轴为直线 x1，抛物线与 x 轴的一个交点在（3，0）和（2， 第 14 页（共 28 页） 0）之间， &
26、nbsp;抛物线与 x 轴的另一个交点在（0，0）和（1，0）之间， x1 时，y0， 即 a+b+c0， b2a， 3a+c0， 故 C 错误； D抛物线开口向下，顶点为（1，n） ， 函数有最大值 n， 抛物线 yax2+bx+c 与直线 yn+1 无交点， 一元二次方程 ax2+bx+cn+1 无实数根， 故 D 正确 故选：C 【点评】本题考查了抛物线与 x 轴的交点：把求二次函数 yax2+bx+c（a，b，c 是常数， a0）与 x 轴的交
27、点坐标问题转化为解关于 x 的一元二次方程也考查了二次函数的性 质 12 （3 分）如图，矩形纸片 ABCD 中，AB6，BC12将纸片折叠，使点 B 落在边 AD 的延长线上的点 G 处，折痕为 EF，点 E、F 分别在边 AD 和边 BC 上连接 BG，交 CD 于点 K，FG 交 CD 于点 H给出以下结论： EFBG； GEGF； GDK 和GKH 的面积相等； 当点 F 与点 C 重合时，DEF75， 其中正确的结论共有（ ） 第 15 页（共 28 页） A1 个 B2
28、 个 C3 个 D4 个 【分析】连接 BE，设 EF 与 BG 交于点 O，由折叠的性质可得 EF 垂直平分 BG，可判断 ；由“ASA”可证BOFGOE，可得 BFEGGF，可判断；通过证明四边形 BEGF 是菱形，可得BEFGEF，由锐角三角函数可求AEB30，可得DEF 75，可判断，由题意无法证明GDK 和GKH 的面积相等，即可求解 【解答】解：如图，连接 BE，设 EF 与 BG 交于点 O， 将纸片折叠，使点 B 落在边 AD 的延长线上的点 G 处， EF 垂直平分 BG， EFBG，BOGO，BEEG，BFFG，
29、故正确， ADBC， EGOFBO， 又EOGBOF， BOFGOE（ASA） ， BFEG， BFEGGF，故正确， BEEGBFFG， 四边形 BEGF 是菱形， BEFGEF， 当点 F 与点 C 重合时，则 BFBCBE12， sinAEB， AEB30， DEF75，故正确， 由题意无法证明GDK 和GKH 的面积相等，故错误； 故选：C 第 16 页（共 28 页）
30、 【点评】本题考查了翻折变换，全等三角形的判定和性质，菱形的判定和性质，锐角三 角函数等知识，灵活运用这些性质进行推理是本题的关键 二、填空题（本题共二、填空题（本题共 4 小题，每小题小题，每小题 3 分，共分，共 12 分）分） 13 （3 分）分解因式：m3m m（m+1） （m1） 【分析】先提取公因式 m，再对余下的多项式利用平方差公式继续分解 【解答】解：m3m， m（m21） ， m（m+1） （m1） 【点评】本题考查提公因式法分解因式和利用平方差公式分解因式，关键在于需要进行 二次分解因式
31、 14 （3 分）一口袋内装有编号分别为 1，2，3，4，5，6，7 的七个球（除编号外都相同） ， 从中随机摸出一个球，则摸出编号为偶数的球的概率是 【分析】用袋子中编号为偶数的小球的数量除以球的总个数即可得 【解答】解：从袋子中随机摸出一个球共有 7 种等可能结果，其中摸出编号为偶数的 球的结果数为 3， 摸出编号为偶数的球的概率为， 故答案为： 【点评】本题主要考查概率公式，解题的关键是掌握随机事件 A 的概率 P（A）事件 A 可能出现的结果数所有可能出现的结果数 15 （3 分）如图，在平面直角坐标
32、系中，O（0，0） ，A（3，1） ，B（1，2） 反比例函数 y （k0）的图象经过OABC 的顶点 C，则 k 2 【分析】连接 OB，AC，根据 O，B 的坐标易求 P 的坐标，再根据平行四边形的性质： 第 17 页（共 28 页） 对角线互相平分即可求出则 C 点坐标，根据待定系数法即可求得 k 的值 【解答】解：连接 OB，AC，交点为 P， 四边形 OABC 是平行四边形， APCP，OPBP， O（0，0） ，B（1，2） ， P 的坐标（，1） ， A（
33、3，1） ， C 的坐标为（2，1） ， 反比例函数 y（k0）的图象经过点 C， k212， 故答案为2 【点评】本题考查的是反比例函数图象上点的坐标特点，平行四边形的性质，求得 C 点 的坐标是解答此题的关键 16 （3 分）如图，在四边形 ABCD 中，AC 与 BD 相交于点 O，ABCDAC90，tan ACB，则 【分析】通过作辅助线，得到ABCANM，OBCODM，ABCDAN，进 第 18 页（共 28 页） 而得出对应边成比例， 再根据 tanACB
34、， 得出对应边之间关系， 设 ABa， DNb，表示 BC，NA，MN，进而表示三角形的面积，求出三角形的面积比即可 【解答】 解： 如图， 过点 D 作 DMBC， 交 CA 的延长线于点 M， 延长 BA 交 DM 于点 N， DMBC， ABCANM，OBCODM， tanACB， 又ABCDAC90， BAC+NAD90， BAC+BCA90， NADBCA， ABCDAN， ， 设 ABa，DNb，则 BC2a，NA2b，MN4b， 由得，D
35、Ma， 4b+ba， 即，ba， 故答案为： 【点评】本题考查相似三角形的性质和判定，根据对应边成比例，设常数表示三角形的 面积是得出正确答案的关键 第 19 页（共 28 页） 三、解答题（本题共三、解答题（本题共 7 小题，共小题，共 52 分）分） 17 （5 分）计算： （） 12cos30+| |（4）0 【分析】根据零指数幂、负整数指数幂、特殊角的三角函数值进行计算即可求解 【解答】解：原式32+31 3+1 2 &nb
36、sp;【点评】本题考查了实数的运算、零指数幂、负整数指数幂、特殊角的三角函数值，解 决本题的关键是掌握特殊角的三角函数值 18 （6 分）先化简，再求值：（2+） ，其中 a2 【分析】先将分式进行化简，然后代入值即可求解 【解答】解：原式 当 a2 时，原式1 【点评】本题考查了分式的化简求值，解决本题的关键是进行分式的化简 19 （7 分）以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业 态发展对人才的需求更加旺盛某大型科技公司上半年新招聘软件、硬件、总线、
37、测试 四类专业的毕业生，现随机调查了 m 名新聘毕业生的专业情况，并将调查结果绘制成如 图两幅不完整的统计图 请根据统计图提供的信息，解答下列问题 第 20 页（共 28 页） （1）m 50 ，n 10 （2）请补全条形统计图； （3）在扇形统计图中， “软件”所对应的扇形的圆心角是 72 度； （4）若该公司新招聘 600 名毕业生，请你估计“总线”专业的毕业生有 180 名 【分析】 （1）根据总线的人数和所占的百分比，可以求得 m 的值，然后即可计算出 n 的 值； （2
38、）根据（1）中的结果和硬件所占的百分比，可以求得硬件专业的毕业生，从而可以 将条形统计图补充完整； （3）根据条形统计图中的数据，可以计算出在扇形统计图中， “软件”所对应的扇形的 圆心角的度数； （4）根据统计图中的数据，可以计算出“总线”专业的毕业生的人数 【解答】解： （1）m1530%50， n%550100%10%， 故答案为：50，10； （2）硬件专业的毕业生有：5040%20（人） ， 补全的条形统计图如右图所示； （3）在扇形统计图中， “软件”所对应的扇形的圆心角是 36072，
39、 故答案为：72； （4）60030%180（名） ， 即“总线”专业的毕业生有 180 名， 故答案为：180 【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确 题意，利用数形结合的思想解答 第 21 页（共 28 页） 20 （8 分）如图，AB 为O 的直径，点 C 在O 上，AD 与过点 C 的切线互相垂直，垂足 为 D连接 BC 并延长，交 AD 的延长线于点 E （1）求证：AEAB； （2）若 AB10，BC6，求 CD 的长
40、 【分析】 （1）证明：连接 AC、OC，如图，根据切线的性质得到 OCCD，则可判断 OC AD，所以OCBE，然后证明BE，从而得到结论； （2）利用圆周角定理得到ACB90，则利用勾股定理可计算出 AC8，再根据等腰 三角形的性质得到 CEBC6，然后利用面积法求出 CD 的长 【解答】 （1）证明：连接 AC、OC，如图， CD 为切线， OCCD， CDAD， OCAD， OCBE， OBOC， OCBB， BE， AEAB； （
41、2）解：AB 为直径， ACB90， AC8， ABAE10，ACBE， CEBC6， 第 22 页（共 28 页） CDAEACCE， CD 【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径；若出现圆的切线， 必连过切点的半径，构造定理图，得出垂直关系也考查了圆周角定理 21 （8 分）端午节前夕，某商铺用 620 元购进 50 个肉粽和 30 个蜜枣粽，肉粽的进货单价 比蜜枣粽的进货单价多 6 元 （1）肉粽和蜜枣粽的进货单价分别是多少元？ &
42、nbsp;（2）由于粽子畅销，商铺决定再购进这两种粽子共 300 个，其中肉粽数量不多于蜜枣粽 数量的 2 倍，且每种粽子的进货单价保持不变，若肉粽的销售单价为 14 元，蜜枣粽的销 售单价为 6 元， 试问第二批购进肉粽多少个时， 全部售完后， 第二批粽子获得利润最大？ 第二批粽子的最大利润是多少元？ 【分析】 （1）设蜜枣粽的进货单价是 x 元，则肉粽的进货单价是（x+6）元，根据用 620 元购进 50 个肉粽和 30 个蜜枣粽，可得出方程，解出即可； （2）设第二批购进肉粽 y 个，则蜜枣粽购进（300y）个，获得利润为 w 元，根据 w 蜜枣粽的利润+肉粽的利
43、润，得一次函数，根据一次函数的增减性，可解答 【解答】解： （1）设蜜枣粽的进货单价是 x 元，则肉粽的进货单价是（x+6）元， 由题意得：50（x+6）+30 x620， 解得：x4， 6+410， 答：蜜枣粽的进货单价是 4 元，则肉粽的进货单价是 10 元； （2）设第二批购进肉粽 y 个，则蜜枣粽购进（300y）个，获得利润为 w 元， 由题意得：w（1410）y+（64） （300y）2y+600， 第 23 页（共 28 页） 20， w 随 y
44、的增大而增大， y2（300y） ， y200， 当 y200 时，w 有最大值，w最大值400+6001000， 答：第二批购进肉粽 200 个时，总利润最大，最大利润是 1000 元 【点评】本题考查了一次函数，一元一次方程及一元一次不等式的知识，解答本题的关 键是仔细审题，找到不等关系及等量关系，难度一般 22 （9 分） 背景： 一次小组合作探究课上， 小明将两个正方形按如图所示的位置摆放 （点 E、 A、D 在同一条直线上） ，发现 BEDG 且 BEDG 小组讨论后，提出了下列三个问题，请你帮助解答
45、： （1）将正方形 AEFG 绕点 A 按逆时针方向旋转（如图 1） ，还能得到 BEDG 吗？若能， 请给出证明；若不能，请说明理由； （2）把背景中的正方形分别改成菱形 AEFG 和菱形 ABCD，将菱形 AEFG 绕点 A 按顺时 针方向旋转（如图 2） ，试问当EAG 与BAD 的大小满足怎样的关系时，背景中的结论 BEDG 仍成立？请说明理由； （3）把背景中的正方形分别改写成矩形 AEFG 和矩形 ABCD，且，AE4， AB8，将矩形 AEFG 绕点 A 按顺时针方向旋转（如图 3） ，连接 DE，BG小组发现： 在旋转过程中，DE2+BG2的
46、值是定值，请求出这个定值 第 24 页（共 28 页） 【分析】 （1）由正方形的性质得出 AEAF，EAG90，ABAD，BAD90， 得出EABGAD，证明AEBAGD（SAS） ，则可得出结论； （2）由菱形的性质得出 AEAG，ABAD，证明AEBAGD（SAS） ，由全等三角 形的性质可得出结论； （3）证明EABGAD，得出BEAAGD，则 A，E，G，Q 四点共圆，得出GQP PAE90，连接 EG，BD，由勾股定理可求出答案 【解答】 （1）证明：四边形 AEFG 为正方形，
47、;AEAF，EAG90， 又四边形 ABCD 为正方形， ABAD，BAD90， EABGAD， AEBAGD（SAS） ， BEDG； （2）当EAGBAD 时，BEDG， 理由如下： EAGBAD， EABGAD， 又四边形 AEFG 和四边形 ABCD 为菱形， AEAG，ABAD， AEBAGD（SAS） ， BEDG； （3）解：如图，设 BE 与 DG 交于 Q， ，AE4，AB8 AG6，
48、AD12 四边形 AEFG 和四边形 ABCD 为矩形， 第 25 页（共 28 页） EAGBAD， EABGAD， ， EABGAD， BEAAGD， A，E，G，Q 四点共圆， GQPPAE90， GDEB， 连接 EG，BD， ED2+GB2EQ2+QD2+GQ2+QB2EG2+BD2， EG2+BD242+62+82+122260 【点评】本题是相似形综合题，考查了正方形的性质，菱形的性质，矩形的性质，
49、全等 三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识，熟练掌握特殊平行 四边形的性质是解题的关键 23 （9 分）如图 1，抛物线 yax2+bx+3（a0）与 x 轴的交点 A（3，0）和 B（1，0） ， 与 y 轴交于点 C，顶点为 D （1）求该抛物线的解析式； （2）连接 AD，DC，CB，将OBC 沿 x 轴以每秒 1 个单位长度的速度向左平移，得到 OBC，点 O、B、C 的对应点分别为点 O、B、C，设平移时间为 t 秒，当点 O与点 A 重合时停止移动记OBC与四边形 AOCD 重合部分的面积为 S，请直接写出 S 与 t 之
50、间的函数关系式； （3）如图 2，过该抛物线上任意一点 M（m，n）向直线 l：y作垂线，垂足为 E，试 问在该抛物线的对称轴上是否存在一点 F，使得 MEMF？若存在，请求出 F 的坐 标；若不存在，请说明理由 第 26 页（共 28 页） 【分析】 （1）将点 A（3，0） 、B（1，0）代入抛物线的解析式得到关于 a、b 的方程组 即可； （2）分三种情况：0t1 时，1t时，t3 时，可由面积公式得出答 案； （ 3 ） 令F （ 1 ， t ）， 则MF ， ME n ，
51、得 出 ，可求出 n则得出答案 【解答】解： （1）抛物线 yax2+bx+3 过点 A（3，0） ，B（1，0） ， ，解得， 抛物线的解析式为 yx22x+3； （2）0t1 时，如图 1， OOt，OB1t， OE3OB33t， S（CO+OE）OO（3+33t）t+3t， 第 27 页（共 28 页） 1t时，S； t3 时，如图 2， AO3，OOt， AO3t，OO62t， CQ2t3， QH2H
52、E，CH3HE， HECD（2t3） ， S（2t3） ， S， 综合以上可得：S （3）令 F（1，t） ，则 MF，MEn， MEMF， MFME， ， m2+2m+1+t22nt nm22m+3， 第 28 页（共 28 页） +（2+4n17）m+1+t26t+0 当 n时，上式对于任意 m 恒成立， 存在 F（1，） 【点评】本题是二次函数的综合题，考查了待定系数法求二次函数的解析式，两点间的 距离公式，平移的性质，三角形的面积等知识熟练运用方程的思想方法，正确进行分 类是解题的关键
