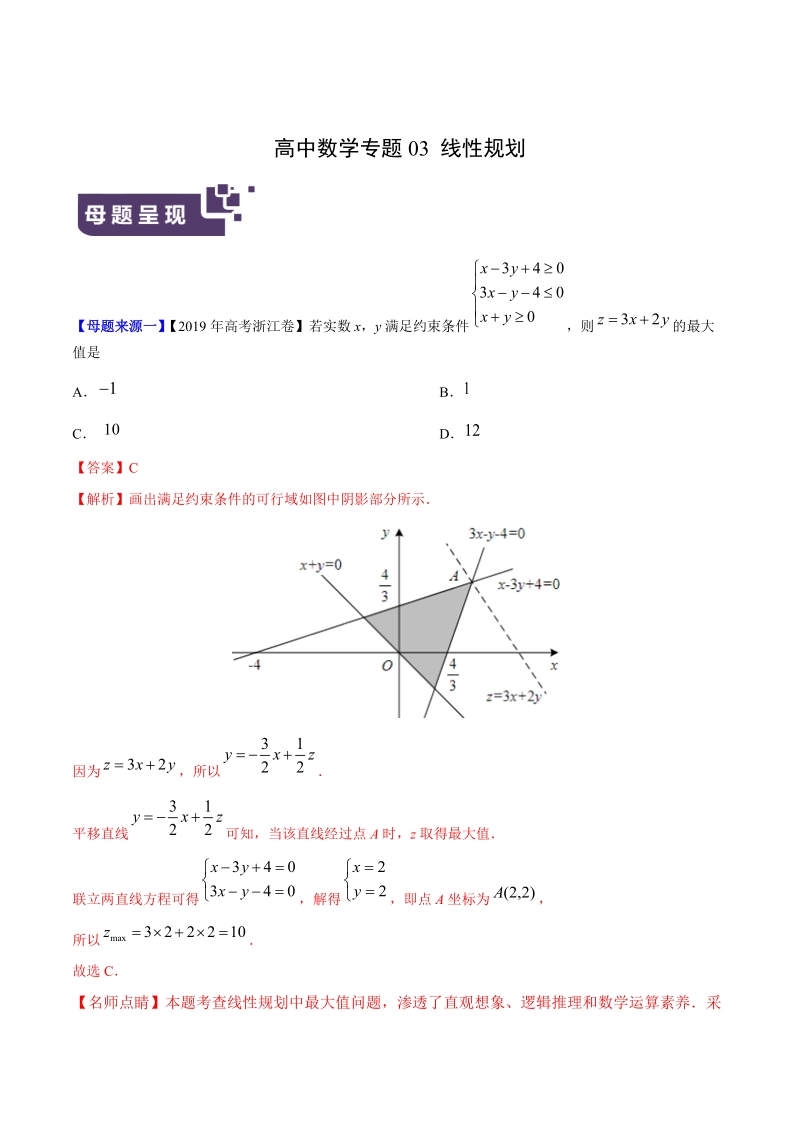
1、高中数学专题03 线性规划【母题来源一】【2019年高考浙江卷】若实数x，y满足约束条件，则的最大值是ABC D【答案】C【解析】画出满足约束条件的可行域如图中阴影部分所示因为，所以平移直线可知，当该直线经过点A时，z取得最大值联立两直线方程可得，解得，即点A坐标为，所以故选C【名师点睛】本题考查线性规划中最大值问题，渗透了直观想象、逻辑推理和数学运算素养采取图解法，利用数形结合思想解题搞不清楚线性目标函数的几何意义致误，从线性目标函数对应直线的截距观察可行域，平移直线进行判断取最大值还是最小值【母题来源二】【2018年高考浙江卷】若，满足约束条件，则的最小值是_，最大值是_【答案】【解析】作
2、出不等式组表示的平面区域如下图中阴影部分所示，则直线过点时取最大值，过点时取最小值【名师点睛】（1）该题考查的是有关线性规划的问题，在求解的过程中，首先需要正确画出约束条件对应的可行域，之后根据目标函数的形式，判断z的几何意义，之后画出一条直线，上下平移，判断哪个点是最优解，从而联立方程组，求得最优解的坐标，代入求值，要明确目标函数的形式大体上有三种：斜率型、截距型、距离型，根据不同的形式，应用相应的方法求解（2）线性规划的实质是把代数问题几何化，即数形结合的思想需要注意的是：准确无误地作出可行域；画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；一般情况下，目标函数
3、的最大或最小值会在可行域的端点或边界上取得【母题来源三】【2017年高考浙江卷】若，满足约束条件，则的取值范围是A0，6B0，4C6，D4，【答案】D【解析】如图，可行域为一开放区域，所以直线过点时取最小值4，无最大值，故选D【名师点睛】本题主要考查线性规划问题，首先由不等式组作出相应的可行域，作图时，可将不等式转化为（或），“”取下方，“”取上方，并明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围【命题意图】了解二元一次不等式的几何意义，能
4、用平面区域表示二元一次不等式组，求出目标函数的最值或取值范围，通过考查线性规划等相关知识，考查数形结合思想的运用【命题规律】这类试题在考查题型上主要以选择题或填空题的形式出现，主要从线性目标函数、斜率型、距离型等角度进行考查，考查数形结合思想试题难度不大，多为中低档题【答题模板】1确定平面区域的方法第一步，“直线定界”，即画出边界，要注意是虚线还是实线；第二步，“特殊点定域”，取某个特殊点作为测试点，由的符号就可以断定表示的是直线哪一侧的平面区域；第三步，用阴影表示出平面区域2在确定线性约束条件和线性目标函数的前提下，用图解法求最优解的步骤可概括为“画、移、求、答”，即：（1）画：在平面直角坐
5、标系中，画出可行域和直线 (目标函数为)；（2）移：平行移动直线，确定使取得最大值或最小值的点；（3）求：求出使z取得最大值或最小值的点的坐标(解方程组)及z的最大值或最小值；（4）答：给出正确答案【方法总结】1二元一次不等式组表示的平面区域的应用主要包括求平面区域的面积和已知平面区域求参数的取值或范围（1）对于面积问题，可先画出平面区域，然后判断其形状（三角形区域是比较简单的情况），求得相应的交点坐标、相关的线段长度等，若图形为规则图形，则直接利用面积公式求解；若图形为不规则图形，则运用割补法计算平面区域的面积，其中求解距离问题时常常用到点到直线的距离公式（2）对于求参问题，则需根据区域的形
6、状判断动直线的位置，从而确定参数的取值或范围2对于二元一次不等式的不同形式，其对应的平面区域有如下结论3线性目标函数的最值问题的求法（1）平移直线法：作出可行域,正确理解z的几何意义，确定目标函数对应的直线，平移得到最优解对一个封闭图形而言,最优解一般在可行域的顶点处取得，在解题中也可由此快速找到最大值点或最小值点 （2）顶点代入法：依约束条件画出可行域;解方程组得出可行域各顶点的坐标;分别计算出各顶点处目标函数的值，经比较后得出z的最大(小)值 求解时需要注意以下几点：（）在可行解中，只有一组(x,y)使目标函数取得最值时，最优解只有1个如边界为实线的可行域，当目标函数对应的直线不与边界平行
7、时，会在某个顶点处取得最值（）同时有多个可行解取得一样的最值时，最优解有多个如边界为实线的可行域，目标函数对应的直线与某一边界线平行时，会有多个最优解（）可行域一边开放或边界线为虚线均可导致目标函数找不到相应的最值，此时也就不存在最优解4距离问题常涉及点到直线的距离和两点间的距离，熟悉这些模型有助于更好地求解非线性目标函数的最值（1）对形如型的目标函数，可先变形为的形式，将问题化为求可行域内的点(x，y)到直线的距离的倍的最值（2）对形如型的目标函数均可化为可行域内的点(x，y)与点(a，b)间距离的平方的最值问题5斜率问题是线性规划延伸变化的一类重要问题，其本质仍然是二元函数的最值问题，不过
8、是用模型形态呈现的因此有必要总结常见模型或其变形形式对形如型的目标函数，可先变形为的形式，将问题化为求可行域内的点(x，y)与点连线的斜率的倍的取值范围、最值等6若目标函数中有参数，要从目标函数的结论入手，对图形进行动态分析，对变化过程中的相关量进行准确定位，这是求解这类问题的主要思维方法7若约束条件中含有参数，则会影响平面区域的形状，这时含有参数的不等式表示的区域的分界线是一条变动的直线，注意根据参数的取值确定这条直线的变化趋势，从而确定区域的可能形状8用线性规划求解实际问题的一般步骤（1）模型建立：正确理解题意，将一般文字语言转化为数学语言，进而建立数学模型，这需要在学习有关例题解答时，仔
9、细体会范例给出的模型建立方法（2）模型求解：画出可行域，并结合所建立的目标函数的特点，选定可行域中的特殊点作为最优解（3）模型应用：将求解出来的结论反馈到具体的实例中，设计出最佳的方案注意：（1）在实际应用问题中变量除受题目要求的条件制约外，可能还有一些隐含的制约条件不要忽略（2）线性目标函数的最优整数解不一定在可行域的顶点或边界处取得，此时不能直接代入顶点坐标求最值，可用平移直线法、检验优值法、调整优值法求解1【2018年11月浙江省学考】若实数，满足x-10x+y-10x-y+10，则的最大值是A1B2C3D4【答案】B【分析】画出约束条件的可行域，即可判断y的最大值的位置，求解即可【解析
10、】作出不等式组表示的平面区域，如下图中阴影部分所示，可行域是三角形的区域，易知点A的纵坐标取得最大值，由x=1x-y+1=0，可得x=1，y=2，所以的最大值是2，故选B2【浙江省浙南名校联盟2019届高三上学期期末联考】设实数满足，则的最小值为ABCD【答案】C【分析】由约束条件作出可行域，再令，化目标函数为，由直线在y轴的截距的范围确定目标函数的最值即可【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，令，则，因此求的最小值，即是求直线在y轴截距的最大值，由图中虚线可知，当虚线过点（0,1）时，直线截距最大，即故选C【名师点睛】本题主要考查简单的线性规划问题，只需由约束条件作出可行
11、域，再化目标函数为直线的斜截式方程即可求解，属于基础题型3【浙江省金华十校2019届第二学期高考模拟】若，满足约束条件，则的最大值是A8B4C2D6【答案】D【分析】先根据约束条件画出可行域，再转化目标函数，把求目标函数的最值问题转化成求截距的最值问题【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由，解得，由，得，平移直线，由图可知当直线经过点，直线的截距最大，此时最大，此时，故选D【名师点睛】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法，属于基础题4【西南名校联盟重庆市第八中学2019届高三5月高考适应性月考】设满足约束条件，
12、则的最大值为AB9C14D18【答案】C【分析】在直角坐标系内，画出可行解域，平行移动直线，直至找到，在轴截距最大时，经过的可行解域内的点，求出的最大值【解析】作出约束条件的可行域如图，可知的最大值在点处取得，故，故选C5【宁夏六盘山高级中学2019届高三下学期第二次模拟】若变量满足约束条件，则的最小值为ABCD【答案】A【分析】根据线性约束条件作出可行域，将线性目标函数化为直线方程，根据目标函数平移得到最优解，再将最优解代入目标函数即可得答案【解析】作出可行域如下图所示，目标函数可化为函数，由图可知，当直线过时，直线在y轴上的截距最小，z有最小值为1故选A6【甘肃省2019年高三第二次高考诊
13、断】若实数满足约束条件，则的最大值与最小值之和为A4B16C20D24【答案】C【解析】画出可行域，如下图中阴影部分所示，当直线与y=-x+4重合时，z最小，z的最小值为4；当直线经过A时z最大，此时A的坐标为A（7，9），z的最大为16，故的最大值与最小值之和为4+16=20，故选C7【浙江省金华十校2019届高三上学期期末联考】若实数x，y满足约束条件，则的最小值是A6B5C4D【答案】C【分析】首先画出可行域，利用目标函数的几何意义求z的最小值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由可得，由得，平移，易知过点A时直线在y上截距最小，所以故选C【名师点睛】本题考查了简单
14、线性规划问题，求目标函数的最值首先画出可行域，利用几何意义求值8【北京市人大附中2019届高考模拟预测卷四】设不等式组表示的平面区域为D若直线上存在区域D上的点，则实数a的取值范围是ABCD【答案】B【分析】由题意作出可行域，利用直线过定点，结合直线的斜率，求得满足直线上存在区域D上的点时的a的范围【解析】作出可行域如下图中阴影部分所示，直线过定点O（0，0），要使直线上存在区域D上的点，则直线的斜率akOB，kOA，联立，得A（1，3），联立，得B（2，1），a，故选B9【陕西省宝鸡市2019届高考模拟检测三】设，满足约束条件，则的最大值为A41B5C25D1【答案】A【分析】先作出不等式组
15、对应的可行域，再利用的几何意义数形结合解答得解【解析】由题得不等式组对应的可行域如下图所示，表示区域内的动点(x，y)到点P(-1，0)的最大距离的平方，联立得点A(3，5)，所以z的最大值为故选A【名师点睛】本题主要考查线性规划求最值，考查两点间的距离公式，意在考查学生对这些知识的理解掌握水平和分析推理能力10【浙江省三校2019年5月份第二次联考】已知实数满足，则A有最小值，无最大值B有最大值，无最小值C有最小值，也有最大值D无最小值，也无最大值【答案】A【分析】作出不等式组表示的可行域，设，则，平移直线可得是否能取得最大值和最小值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，
16、设，则，表示直线在轴上的截距的相反数，平移直线，可得当直线过点时取得最小值，没有最大值故选A【名师点睛】本题考查线性规划问题，解题关键是作出不等式组表示的平面区域并弄清目标函数的几何意义11【浙江省七彩联盟2018-2019学年第一学期高三11月期中考试】设实数x，y满足x-y0x+y1x+2y1，则z=2x-y的最小值为A-2B13C12D2【答案】B【分析】作出不等式组对应的平面区域，根据直线平移即可求出目标函数的最小值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由z=2x-y得y=2x-z，平移直线y=2x-z，由图可知，当直线y=2x-z经过A时，直线的截距最大，此时z最
17、小，由x+2y=1x-y=0可得A(13,13)，此时z最小值为z=23-13=13，故选B【名师点睛】本题主要考查线性规划的应用，利用数形结合求出目标函数的最优解，利用数形结合是解决本题的关键12【新疆乌鲁木齐市2019届高三第二次诊断性测试】若变量满足约束条件，则的最大值是A0B2C5D6【答案】C【分析】由题意作出不等式组所表示的平面区域，将化为，相当于直线的纵截距，由几何意义可得结果【解析】由题意作出其平面区域，如下图中阴影部分所示，令，化为，相当于直线的纵截距，由图可知，解得，则的最大值是，故选C【名师点睛】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题求目标函数最值的一
18、般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值13【辽宁省辽阳市2019届高三二模】设，满足约束条件，则目标函数的最小值是A-4B-2C0D2【答案】A【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，进行求解即可【解析】作出不等式组对应的平面区域如图（阴影部分），由得，平移直线，由图象可知当直线，过点时，直线的截距最大，此时最小，由，解得代入目标函数，得，目标函数的最小值是故选A【名师点睛】本题主要考查线性规
19、划的基本应用，利用目标函数的几何意义是解决问题的关键，利用数形结合是解决问题的基本方法，属于基础题14【浙江省湖州三校2019年普通高等学校招生全国统一考试】若变量，满足约束条件，则的最大值是A1B2C3D4【答案】D【分析】先作可行域，再求的取值范围，最后可得的最大值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，则直线过点时取最小值，过点时取最大值2，因此的最大值是4，故选D15【山东省实验中学等四校2019届高三联合考试】已知实数，满足约束条件，则目标函数的最小值为ABCD【答案】B【解析】作出不等式组对应的平面区域如图：目标函数的几何意义为动点到定点的斜率，当位于时，此时的斜
20、率最小，此时故选B【名师点睛】本题主要考查线性规划的应用以及两点之间的斜率公式的计算，利用z的几何意义，通过数形结合是解决本题的关键16【广东省韶关市2019届高考4月模拟测试】若，满足约束条件，则的最大值为ABC5D6【答案】C【解析】变量，满足约束条件的可行域如图中阴影部分所示：目标函数是斜率等于1、纵截距为的直线，当直线经过可行域的点时，纵截距取得最小值，则此时目标函数取得最大值，由可得，目标函数的最大值为5故选C【名师点睛】本题考查线性规划的简单应用，考查计算能力以及数形结合思想的应用17【浙江省杭州市学军中学2018-2019学年高二上学期期中考试】设x，y满足约束条件2x+3y-3
21、02x-3y+30y+30，则z=2x+y的最小值是A1B9C-15D-9【答案】C【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，z=2x+y化为y=-2x+z，平移直线y=-2x+z，y=-2x+z经过可行域的A时，目标函数取得最小值，由y=-32x-3y+3=0，解得A-6,-3，则z=2x+y的最小值是-15，故选C【名师点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题求目标函数最值的一般步骤是“一画、二移、三求”：（
22、1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值18【黑龙江省大庆市2019届高三第三次教学质量检测】已知实数，满足，则的最小值为A0BCD-2【答案】D【分析】画出不等式组表示的可行域，由得，平移直线，结合图形可得取得最小值时的最优解，进而得到最小值【解析】画出不等式组表示的可行域，如图中阴影部分所示由得平移直线，结合图形可得，当直线经过可行域内的点时，直线在y轴上的截距最小，此时z取得最小值，所以故选D【名师点睛】利用线性规划求目标函数的最值问题是常
23、考题型，一般以选择题、填空题的形式出现，难度适中解题时要熟练画出可行域，把目标函数适当变形，把所求最值转化为求直线的斜率、截距、距离等问题处理，主要考查数形结合在解题中的应用和计算能力19【新疆乌鲁木齐2019届高三第二次质量检测】若实数x，y满足，则函数的最大值为A12BC3D15【答案】A【分析】画出可行域，然后平移直线，找到在轴截距最大时，直线经过的点，代入，即可求出函数的最大值【解析】作出不等式组对应的平面区域如图（阴影部分），由得，平移直线，由图象可知当直线经过点A时，直线在轴的截距最大，此时z最大由，解得，即A（5，2），代入目标函数得z=25+2=12即目标函数的最大值为12故选
24、A20【浙北四校2019届高三12月模拟考试】若直线ax+by=1与不等式组y12x-y-102x+y+10表示的平面区域无公共点，则2a+3b的取值范围是A-7，1B-3，5C-7，3DR【答案】C【分析】作出不等式组对应的平面区域，利用直线ax+by=1与平面区域无公共点建立条件关系，即可得到结论【解析】作出不等式组表示的平面区域，可知该不等式组表示的平面区域是由A（1，1），B（1，1），C（0，1）围成的三角形区域（包含边界）直线ax+by=1与y12x-y-102x+y+10表示的平面区域无公共点，a，b满足：a+b-10-a+b-10-b-10或a+b-10-a+b-10-b-10
25、（a，b）在如图所示的三角形区域（除边界且除原点）设，平移直线，当直线经过点A1（0，1）时，z取得最大为，当经过点B1时，z最小，由-b-1=0-a+b-1=0解得a=-2b=-1，即B1（2，1），此时z=43=7，故2a+3b的取值范围是（7，3）故选C21【辽宁省丹东市2019届高三总复习质量测试二】设，满足约束条件，则的最大值为_【答案】【分析】画出可行解域，平移直线，找到的最大值【解析】作出不等式组表示的平面区域如下图中阴影部分所示，当直线经过点时，有最大值，解得，所以22【内蒙古呼伦贝尔市2019届高三模拟统一考试一】若满足，则目标函数的最大值为_【答案】【分析】由约束条件作出可
26、行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案【解析】由约束条件作出可行域如下图中阴影部分所示，化目标函数为，由图可得，当直线过点时，直线在轴上的截距最大，由得即，则有最大值，故答案为23【陕西省西安市2019届高三第三次质量检测】若实数x，y满足约束条件x+y1x-y1x0，则z=x-2y的最大值是_【答案】2【分析】作出不等式组表示的平面区域，平移目标函数所表示的直线，可得出目标函数的最大值【解析】作出不等式组表示的平面区域如下图中阴影部分所示，z=x-2y可变形为y=x2-z2，表示斜率为12的直线，平移该直线，当直线经过点A0，-1时，z取得最
27、大值，故zmax=0-2(-1)=224【甘肃省、青海省、宁夏回族自治区2019届高三5月联考】设，满足约束条件，则的最小值是_【答案】0【分析】由约束条件作出可行域，再由目标函数可化为，当直线在轴截距最小时，目标函数取最小值，结合图象即可得出结果【解析】由约束条件作出可行域如下：因为目标函数可化为，所以，当直线在轴截距最小时，目标函数取最小值，由图象可得，当直线过点时，截距最小，即最小；易知，所以故答案为025【浙江省台州市2019届高三上学期期末质量评估】已知，满足条件，则的最大值是_，原点到点的距离的最小值是_【答案】【分析】画出不等式组对应的可行域，通过平移动直线求目标函数的最大值，而
28、原点到点的距离的最小值就是原点到点的距离【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，当动直线过时，有最大值，易得，故的最大值为原点到点的距离的最小值即为26【陕西省2019年高三第三次教学质量检测】设满足约束条件，则的最小值是_【答案】【分析】画出约束条件所表示平面区域，结合图象，确定目标函数的最优解，代入即可求得结果【解析】作出不等式组表示的平面区域如下图中阴影部分所示，目标函数化为，当直线过点A时，此时在y轴上的截距最大，目标函数取得最小值，又由，解得，所以目标函数的最小值为27【甘肃省兰州市第一中学2019届高三6月最后高考冲刺模拟】若满足约束条件则的最小值为_【答案】【分
29、析】先由约束条件作出可行域，再由目标函数可化为，因此当直线在轴上截距最小时，取最小，结合图象即可求出结果【解析】作出不等式组表示的平面区域如下图中阴影部分所示，因为目标函数可化为，因此当直线在轴上截距最小时，取最小由图象易得，当直线过点时，在轴上截距最小，即故答案为【名师点睛】本题主要考查简单的线性规划，只需由约束条件作出可行域，分析目标函数的几何意义，结合图象即可求解，属于常考题型28【浙江省金丽衢十二校2019届高三第二次联考】若实数，满足约束条件，则目标函数的最小值为_；最大值为_【答案】【分析】作出可行域，由可得，作出直线，平移直线当截距最大时，z有最大值，平移直线当截距最小时，z有最
30、小值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由可得，作出直线，平移直线过B(1，0)时，z有最小值，平移直线过A(1，）时，z有最大值29【浙江省金华市浦江县2019年高考适应性考试】已知实数x，y满足x-y1x+y1x0，则此平面区域的面积为_，的最大值为_【答案】12【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，则其围成的平面区域的面积为12211；的最大值为过点（1,0）时取得最大值，最大值为230【浙江省温州九校2019届高三第一次联考】已知点P(x，y)在不等式组x-y+50yay-2x0，表示的平面区域D上运动，若区域D表示一个三角形，则a的取值范围是
31、_，若，则的最大值是_【答案】【分析】根据已知的不等式组画出满足条件的可行域，根据图形情况讨论，求出表示的平面区域是一个三角形时a的取值范围，进而得到时的最大值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由图可知，若不等式组x-y+50yay-2x0表示的平面区域是一个三角形，则a10，故a的取值范围是若，可知当目标函数经过点A（1,2）时取得最大值，最大值是31【浙江省嘉兴市2019届高三第一学期期末检测】在平面直角坐标系中，不等式组所表示的平面区域的面积等于_，的取值范围是_【答案】【分析】先根据约束条件画出可行域，再利用几何意义求面积，只需求出区域图形的面积即可；将目标函数
32、化为斜截式，根据图像分析得到最值【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由可得C（1，0），由可得B（1，4），由可得A（0，1），故该不等式组所表示的平面区域的面积为412目标函数，易知过点A时取得最小值1，过点B时取得最大值6故的取值范围是【名师点睛】利用线性规划求最值的步骤：在平面直角坐标系内作出可行域；考虑目标函数的几何意义，将目标函数进行变形常见的类型有截距型（型）、斜率型（型）和距离型（型）；确定最优解：根据目标函数的类型，并结合可行域确定最优解；求最值：将最优解代入目标函数即可求出最大值或最小值32【浙江省2019年高考模拟训练三】若实数满足不等式组，则的最大值
33、为_【答案】【分析】作出不等式组对应的平面区域，利用数形结合即可得到结论【解析】由zy2x，得y2x+z，作出不等式组表示的平面区域，如下图中阴影部分所示，平移直线y2x+z，由平移可知当直线y2x+z经过点A时，线y2x+z的截距最大，此时z取得最大值，由，得，即A（-3，4），代入zy2x，得z42（-3）10，即zy2x的最大值为1033【广东省深圳市深圳外国语学校2019届高三第二学期第一次热身考试】已知实数，满足，则的最大值是_【答案】【解析】由约束条件可知可行域为图中阴影部分所示：其中，又，可知的几何意义为可行域中的点到直线距离的倍，可行域中点到直线距离最大的点为，故填【名师点睛】
34、本题考查利用线性规划求解最值的问题，关键是能够明确目标函数所表示的几何意义，利用数形结合来进行求解34【重庆西南大学附属中学校2019届高三第十次月考】已知x，y满足约束条件，则的取值范围为_【答案】【解析】作出不等式组表示的平面区域如下图中阴影部分所示，因目标函数可化为，所以目标函数表示直线在轴截距的相反数，根据图象可得，当直线过点时，截距最小，即最大；当直线过点时，截距最大，即最小；由题意易得；由得，因此，所以的取值范围为【名师点睛】本题主要考查简单的线性规划，只需由约束条件作出可行域，根据目标函数的几何意义即可求解，属于常考题型35【浙江省衢州市五校联盟2019届高三年级上学期联考】若x
35、，y满足x-y+10x+y-303x-y-50，z=2x+y的最小值为_；z=y+xx的最大值为_【答案】43【分析】由约束条件作出可行域，目标函数转化为为直线方程的斜截式、可行域内的点与原点连线斜率，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论【解析】作出不等式组表示的平面区域，如下图中阴影部分所示，由，可得，将z=2x+y变形为y=-2x+z，平移直线y=-2x+z，由图可知当直y=-2x+z经过点A1，2时，直线在y轴上的截距最小，最小值为z=21+2=4；z=y+xx=yx+1，yx表示可行域内的点与原点连线的斜率，由图可知，yx的最大值为kOA=2，yx+1的最大值为2+1=3【名师点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题求目标函数最值的一般步骤是“一画、二找、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移或旋转变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值
