1、综合模拟测试三(时间:120分钟总分:120分)一、选择题(每小题3分,共30分)1.方程x2+x-12=0的两个根为()A.x1=-2,x2=6B.x1=-6,x2=2C.x1=-3,x2=4D.x1=-4,x2=3答案D2.下列等式一定成立的是()A.a2a3=a5B.(a-b)2=a2-b2C.(2ab2)3=6a3b6D.(x-a)(x-b)=x2-(a+b)x+ab答案D3.在下列命题中,是真命题的是()A.位似图形一定是相似图形B.等腰梯形既是轴对称图形又是中心对称图形C.四条边相等的四边形是正方形D.垂直于同一条直线的两条直线互相垂直答案A4.若不等式组x+9m+1的解集是x2,
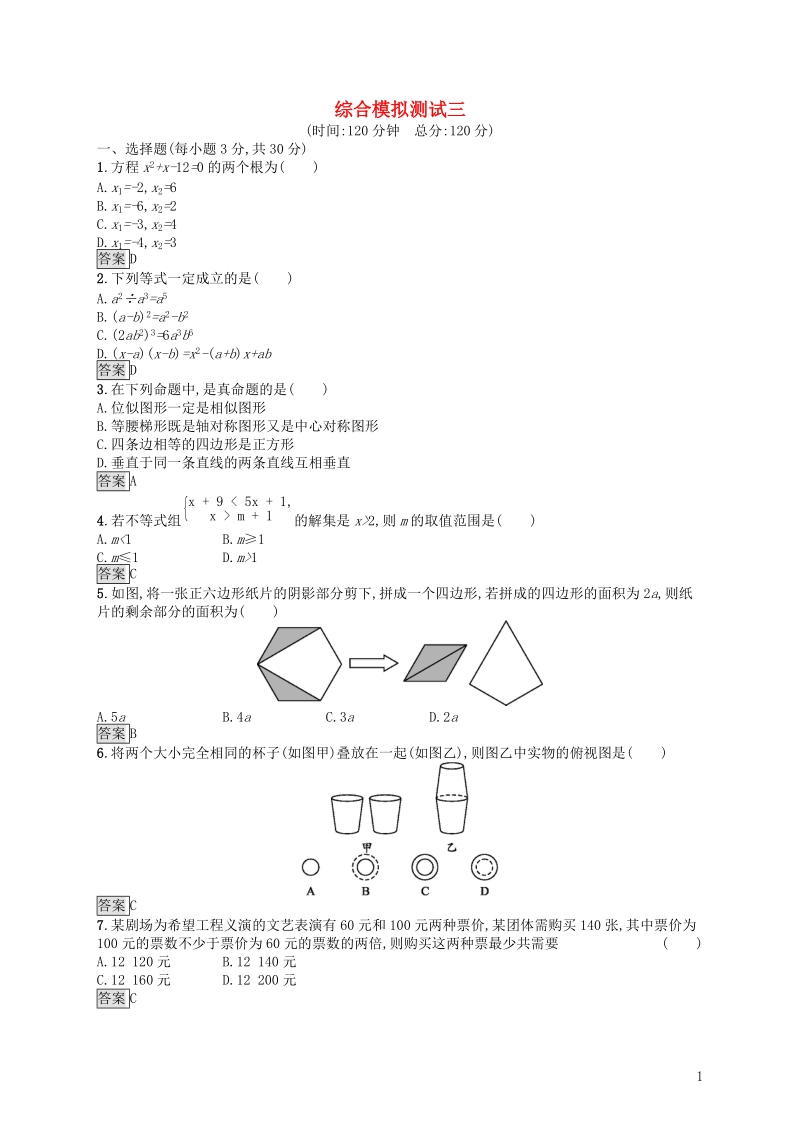
2、则m的取值范围是()A.m1答案C5.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为()A.5aB.4aC.3aD.2a答案B6.将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是()答案C7.某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要()A.12 120元B.12 140元C.12 160元D.12 200元答案C8.经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能
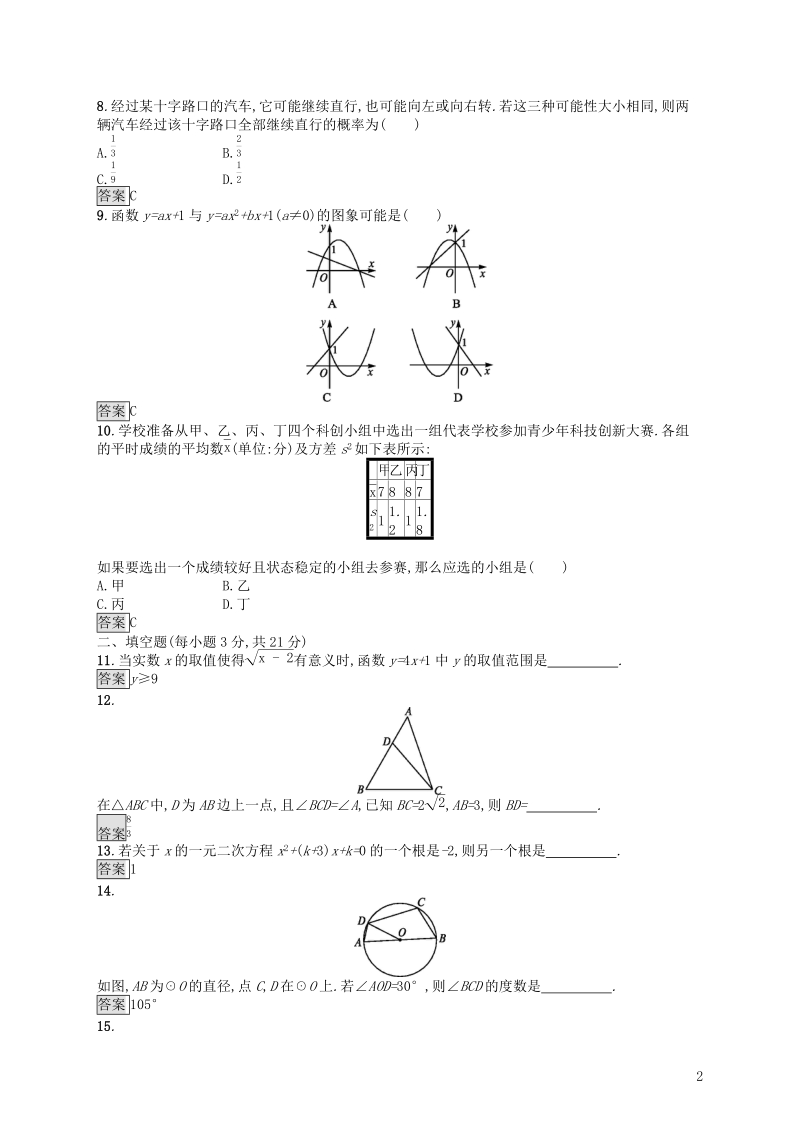
3、性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为()A.13B.23C.19D.12答案C9.函数y=ax+1与y=ax2+bx+1(a0)的图象可能是()答案C10.学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛.各组的平时成绩的平均数x(单位:分)及方差s2如下表所示:甲乙丙丁x7887s211.211.8如果要选出一个成绩较好且状态稳定的小组去参赛,那么应选的小组是()A.甲B.乙C.丙D.丁答案C二、填空题(每小题3分,共21分)11.当实数x的取值使得x-2有意义时,函数y=4x+1中y的取值范围是.答案y912.在ABC中,D为AB边上一点,且
4、BCD=A,已知BC=22,AB=3,则BD=.答案8313.若关于x的一元二次方程x2+(k+3)x+k=0的一个根是-2,则另一个根是.答案114.如图,AB为O的直径,点C,D在O上.若AOD=30,则BCD的度数是.答案10515.如图,甲、乙两盏路灯底部间的距离是30 m,一天晚上,当小华走到距路灯乙底部5 m处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5 m,则路灯甲的高(不带灯罩)为m.答案916.如图,ACB=90,D为AB的中点,连接DC并延长到点E,使CE=14CD,过点B作BFDE交AE的延长线于点F.若BF=10,则AB的长为.答案817.如图,在
5、ABC中,AB=BC,将ABC绕点B顺时针旋转度,得到A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F,下列结论:CDF=,A1E=CF,DF=FC,AD=CE,A1F=CE.其中正确的是(写出正确结论的序号).答案三、解答题(69分)18.(6分)先化简,再求值:n2n-m-m-nm2,其中m-n=2.解原式=n2n-m-(m+n)1m2=n2-n2+m2n-m1m2=m2n-m1m2=1n-m.m-n=2,n-m=-2.原式=1n-m=1-2=-22.19.(8分)如图,点P的坐标为2,32,过点P作x轴的平行线交y轴于点A,交双曲线y=kx(x0)于点N,作PMAN交双
6、曲线y=kx(x0)于点M,连接AM.已知PN=4.(1)求k的值;(2)求APM的面积.解(1)P2,32,PN=4,N6,32.把N6,32代入y=kx,得k=9.(2)PMAN,P2,32,M(2,y),k=9,点M在双曲线y=kx上,把M(2,y)代入y=9x,得y=92.M2,92.又P2,32,MP=3,AP=2.SAPM=1223=3.20.(8分)为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:(1)该班级女生人数是,女生收看“两会”新闻次数
7、的中位数是;(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生的人数;(3)为进一步分析该班级男生、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如下表).统计量平均数中位数众数方差该班级男生3342比较该班级男生、女生收看“两会”新闻次数的波动大小.解(1)203(2)由题意得该班女生对“两会”新闻的“关注指数”为1320100%=65%,所以男生对“两会”新闻的“关注指数”为60%.设该班男生有x人,则x-(1+3+6)x=60
8、%,解得x=25.故该班男生有25人.(3)该班级女生收看“两会”新闻次数的平均数为12+25+36+45+5220=3,女生收看“两会”新闻次数的方差为2(3-1)2+5(3-2)2+6(3-3)2+5(3-4)2+2(3-5)220=1310,因为21310,所以男生比女生的波动幅度大.21.(10分)为创建“国家卫生城市”,进一步优化市中心城区的环境,某市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施进行更新改造,根据市政的建设需要,需在60天内完成此工程.现在甲、乙两个工程队有能力承包这个工程.经调查:乙队单独完成此项工程的时间比甲队单独完成多用25天,甲、乙两队合作完成此项工
9、程需要30天,甲队每天的工程费用是2 500元,乙队每天的工程费用是2 000元.(1)甲、乙两个工程队单独完成各需多少天?(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.解(1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需(x+25)天.根据题意得30x+30x+25=1,即x2-35x-750=0.解得x1=50,x2=-15.经检验,x1=50,x2=-15都是原方程的解.但x2=-15不符合题意,应舍去.所以x=50.当x=50时,x+25=75.故甲工程队单独完成该工程需50天,则乙工程队单独完成该工程需75天.(2)此问题只要设计出符合条件的一种方案即可.
10、有如下两种方案可供选择.方案一:由甲工程队单独完成.所需费用为250050=125000(元).方案二:甲、乙两队合作完成.所需费用为(2500+2000)30=135000(元).22.(12分)已知AB是O的直径,点P在弧AB上(不含点A,B),把AOP沿OP对折,点A的对应点C恰好落在O上.(1)当点P在AB上方而点C在AB下方时(如图),判断PO与BC的位置关系,并证明你的判断;(2)当点P,C都在AB上方时(如图),过点C作CD直线AP于点D,且PC=2PD,证明:CD是O的切线.图图(1)解POBC.理由如下:如图,AOP沿OP对折,点A的对应点C恰好落在O上,1=2.OA=OP,
11、A=1.A=2.A=3,2=3.POBC.图图(2)证明如图,CD直线AP,PDC=90.PC=2PD,1=30.2=60.AOP沿OP对折,点A的对应点C恰好落在O上,3=4.3=12(180-60)=60.而OP=OC,OPC为等边三角形.5=60.OCD=1+5=90.OCCD,CD是O的切线.23.(12分)已知ABC,分别以AB,AC为边作ABD和ACE,且AD=AB,AC=AE,DAB=CAE,连接DC与BE,G,F分别是DC与BE的中点.(1)探索发现:如图,若DAB=60,则AFG=;如图,若DAB=90,则AFG=.(2)探究证明:如图,若DAB=,试探究AFG与的数量关系?
12、并给予证明.(3)动手实践:如果ACB为锐角,ABAC,BAC90,点M在线段BC上运动,连接AM,以AM为一边,以点A为直角顶点,且在AM的右侧作等腰直角AMN,连接NC.试探究:若NCBC(点C,M重合除外),则ACB等于多少度?请同学们自己动手画出相应图形.(画图不写作法)解(1)6045(2)连接AG,DAB=CAE,DAC=BAE.又AD=AB,AC=AE,ADCABE(SAS).1=2.又DG=12DC,BF=12BE,于是DG=BF,且AD=AB,ADGABF(SAS).AG=AF,且DAG=BAF,于是易得GAF=DAB=.也就是说AGF是顶角为的等腰三角形,AFG=90-2.
13、(3)简易画图步骤:1.先画等腰直角三角形AMN;2.找个点C,使得CMCN;3.在CM的延长线上任取一点B,连接AB,AC.(作图不计分)过点A作AC的垂线交BC于点G,由于1和2均与MAC互余,1=2.由于3和4均与ACM互余,3=4.又AM=AN,AMGANC(AAS).AG=AC.又AGAC,AGC为等腰直角三角形.ACB=ACG=45.24.(13分)如图,已知抛物线C0:y=x2,顶点记作A0.首先我们将抛物线C0关于直线y=1对称翻折过去得到抛物线C1称为第一次操作,再将抛物线C1关于直线y=2对称翻折过去得到抛物线C2称为第二次操作,将抛物线Cn-1关于直线y=2n-1对称翻折
14、过去得到抛物线Cn(顶点记作An)称为第n次操作(n=1,2,3).设抛物线C0与抛物线C1交于两点B0与B1,顺次连接A0,B0,A1,B1四个点得到四边形A0B0A1B1,抛物线C2与抛物线C3交于两点B2与B3,顺次连接A2,B2,A3,B3四个点得到四边形A2B2A3B3,抛物线Ck-1与抛物线Ck交于两点Bk-1与Bk,顺次连接Ak-1,Bk-1,Ak,Bk四个点得到四边形Ak-1Bk-1AkBk(k=1,3,5).(1)请分别直接写出抛物线Cn(n=1,2,3,4)的解析式.(2)一系列四边形Ak-1Bk-1AkBk(k=1,3,5)为哪种特殊的四边形(说明理由)?它们都相似吗?如
15、果全都相似,请证明之;如果不全都相似,请举出一对不相似的反例.(3)试归纳出抛物线Cn的解析式,无需证明.并利用你归纳出来的Cn的解析式求四边形Ak-1Bk-1AkBk(k=1,3,5)的面积(用含k的式子表示).解(1)C1:y=-x2+2;C2:y=x2+2;C3:y=-x2+6;C4:y=x2+10.(2)根据抛物线的对称性以及翻折的原理不难得出四边形Ak-1Bk-1AkBk(k=1,3,5)的两条对角线Bk-1Bk与Ak-1Ak互相垂直且平分,故一系列四边形Ak-1Bk-1AkBk均为菱形;它们并不都相似,反例:四边形A0B0A1B1和四边形A2B2A3B3不相似,理由如下:不难算出A
16、0A1=B0B1=2,于是四边形A0B0A1B1为正方形.而A2A3=4,B2B3=22,即A2A3B2B3,四边形A2B2A3B3为菱形.故它们不相似.(3)抛物线Cn的解析式为y=x2+2n+1-23(n为偶数),-x2+2n+1+23(n为奇数).或y=(-1)nx2+2n+1+(-1)n+123由于四边形Ak-1Bk-1AkBk(k=1,3,5)是抛物线Ck-1关于直线y=2k-1翻折得到抛物线Ck后连接交点和顶点所形成的图形,利用上述结论不难得出:Ak-1Ak=2k+1+23-2k-23=2k+43.Ck-1:y=x2+2k-23,Ck:y=-x2+2k+1+23xBk-1=-2k-1+23,xBk=2k-1+23,Bk-1Bk=xBk-xBk-1=22k-1+23.SAk-1Bk-1AkBk=12Ak-1AkBk-1Bk=2k+432k-1+23=239(2k-1+2)2k-1+2.8
