1、图形变换有关的计算与证明1.一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角形的斜边上，AC与DM ， DN分别交于点E ， F ， 把DEF绕点D旋转到一定位置，使得DE=DF ， 则BDN的度数是（）A.105B.115C.120D.1352.如图所示，OAC和BAD都是等腰直角三角形，ACO=ADB=90，反比例函数y= 在第一象限的图象经过点B，与OA交于点P，且OA2AB2=18，则点P的横坐标为（ ） A.9B.6C.3D.3 3.如图，在RtABC中，B=90，AB=BC=2，将ABC绕点C顺时针旋转60，得到DEC，则AE的长是_ 4.如图28-1-1-1所示，
2、某斜坡AB上有一点B，BC、BC是边AC上的高，则图中相似的三角形是_，则BCAB=_,BCAC=_.5.如图，正方形ABCD中，E为BC上一点，BE=2CE，连接DE，F为DE中点，以DF为直角边作等腰RtDFG，连接BG，将DFG绕点D顺时针旋转得DFG，G恰好落在BG的延长线上，连接FG，若BG=2 ，则SGFG=_6.如图，将半径为2，圆心角为120的扇形OAB绕点A逆时针旋转60，点O，B的对应点分别为O，B，连接BB，则图中阴影部分的面积是7.如图，COD是AOB绕点O顺时针方向旋转40后所得的图形，点C恰好在AB上，AOD=90，则D的度数是_ 8.如图，在平行四边形ABCD中，
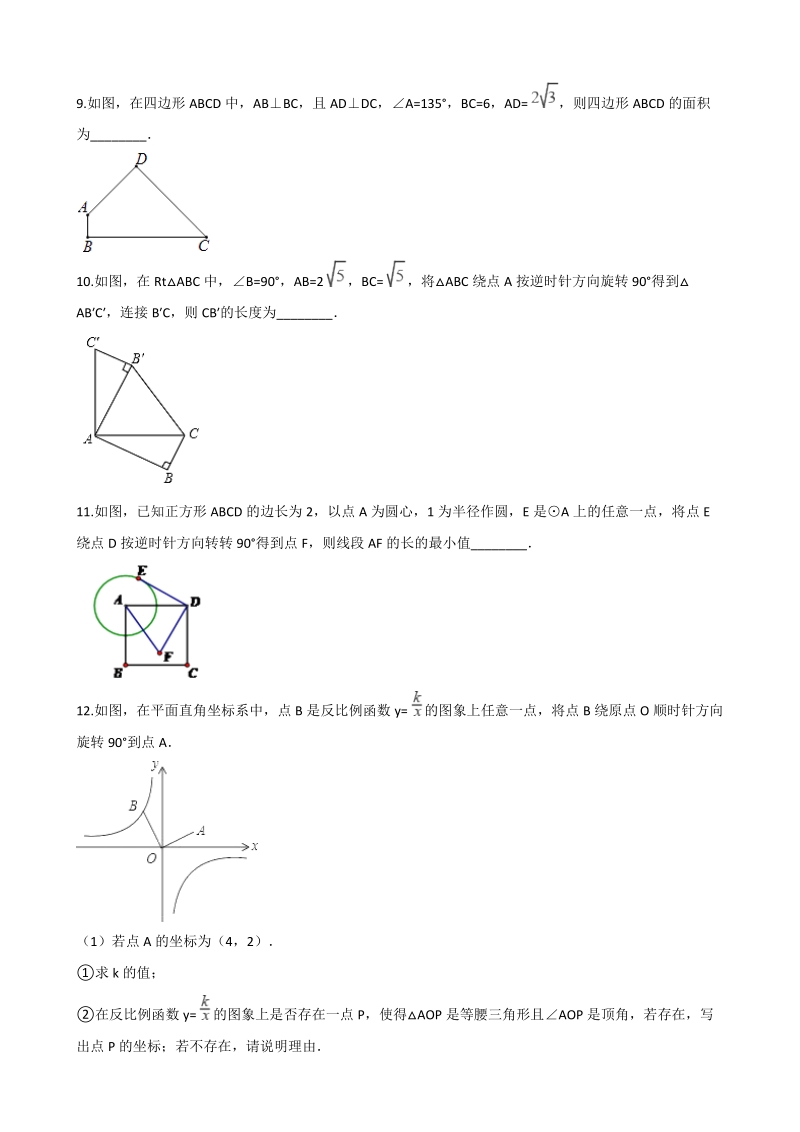
3、AEBC，垂足为E，如果AB=5，BC=8，sinB= ，那么 =_.9.如图，在四边形ABCD中，ABBC，且ADDC，A=135，BC=6，AD= ，则四边形ABCD的面积为_10.如图，在RtABC中，B=90，AB=2 ，BC= ，将ABC绕点A按逆时针方向旋转90得到ABC，连接BC，则CB的长度为_ 11.如图，已知正方形ABCD的边长为2，以点A为圆心，1为半径作圆，E是A上的任意一点，将点E绕点D按逆时针方向转转90得到点F，则线段AF的长的最小值_12.如图，在平面直角坐标系中，点B是反比例函数y= 的图象上任意一点，将点B绕原点O顺时针方向旋转90到点A（1）若点A的坐标为
4、（4，2）求k的值；在反比例函数y= 的图象上是否存在一点P，使得AOP是等腰三角形且AOP是顶角，若存在，写出点P的坐标；若不存在，请说明理由（2）当k=1，点B在反比例函数y= 的图象上运动时，判断点A在怎样的图象上运动？并写出表达式13.如图，菱形ABCD的对角线AC，BD相交于点O，点E，F分别是边AB，AD的中点（1）请判断OEF的形状，并证明你的结论；（2）若AB=13，AC=10，请求出线段EF的长14.在平面直角坐标系xOy中，已知点A的坐标为（0，1），点C（m，0）是x轴上的一个动点 （1）如图1，点B在第四象限，AOB和BCD都是等边三角形，点D在BC的上方，当点C在x轴
5、上运动到如图所示的位置时，连接AD，请证明ABDOBC； （2）如图2，点B在x轴的正半轴上，ABO和ACD都是等腰直角三角形，点D在AC的上方，D=90，当点C在x轴上运动（m1）时，设点D的坐标为（x，y），请探求y与x之间的函数表达式； （3）如图3，四边形ACEF是菱形，且ACE=90，点E在AC的上方，当点C在x轴上运动（m1）时，设点E的坐标为（x，y），请探求y与x之间的函数表达式 15.如图，在四边形ABCD中，ABCD，AB=CD=15，AC平分BAD，AC与BD交于点O，将ABD绕点D顺时针方向旋转，得到EFD，旋转角为（0180）点A的对应点为点E，点B的对应点为点F（1
6、）求证：四边形形ABCD是菱形（2）若BAD=30，DE边为与AB边相交于点M，当点F恰好落在AC上时，求证：MD=ME（3）若ABD的周长是48，EF边与BC边交于点N，DF边与BC边交于点P，在旋转的过程中，当FNP是直角三角形是，FNP的面积是多少16.写出命题“等腰三角形底边上的高线与顶角平分线重合”的逆命题，这个逆命题是真命题吗？请证明你的结论 17.如图，将等腰ABC绕顶点B逆时针方向旋转度到A1B1C1的位置，AB与A1C1相交于点D，AC与A1C1、BC1分别交于点E、F.（1）求证：BCFBA1D（2）当C=度时，判定四边形A1BCE的形状并说明理由。 参考答案 1. C 2
7、.C 3.+ 4. ABCABC；BCAB；BCAC 5.6. 7.60 8.9.12 10.5 11.12.（1）解：过点A作AEx轴于点E，过点B作BFx轴于点F，如图1所示BFx轴，AEx轴，BFO=OEA=90，OBF+BOF=90，BOF+AOE=90，OBF=AOE在BOF和OAE中，有 BOFOAE（AAS），OF=AE，BF=OE点A（4，2），点B（2，4）点B在反比例函数y= 的图象上，k=24=8假设存在，设点P的坐标为（m，n），AOP是等腰三角形且AOP是顶角，OA=OP又点P在反比例函数y= 的图象上， 解得： ， ， ， 故在反比例函数y= 的图象上存在一点P，使
8、得AOP是等腰三角形且AOP是顶角，点P的坐标为（4，2），（2，4），（2，4）或（4，2）（2）解：设点B的坐标为（a，b），由（1）可知点A的坐标为（b，a），k=1，且点B在反比例函数y= 的图象上运动，ab=1，b（a）=ab=1，点A在y= 上运动.13.（1）解：OEF是等腰三角形，理由：四边形ABCD是菱形，AB=AD，ACBD，点E，F分别是边AB，AD的中点，EO=AB，OF=AD，EO=FO，OEF是等腰三角形；（2）解：四边形ABCD是菱形，AC=10，AO=5，AOB=90，BO=12，BD=24，点E，F分别是边AB，AD的中点，EFBD，EF=1214.（1）解：
9、AOB和BCD都是等边三角形， AB=OB，BD=BC，ABO=DBC=60，ABD=OBC，在ABD和OBC中，ABD和OBC；（2）解：如图，过点D作DHy轴，垂足为H，延长HD，过点C作CGHD，垂足为G AHD=CGD=90，ABO和ACD都是等腰直角三角形，ADC=90，AD=CD，ADH+CDG=90，ADH+DAH=90，CDG=DAH，在AHD和DGC中，AHDDGC（AAS），DH=CG=OH，点D的坐标为（x，y），y与x之间的关系是y=x（3）解：过点E作EMx轴，垂足为M，则EMC=COA=90， 四边形ACEF是菱形，且ACE=90，AC=CE，ACO+ECO=90，
10、ACO+CAO=90，ECO=CAO，在EMC和COA中，EMCCOA（AAS），MC=OA=1，EM=OC，点E的坐标为（x，y），EM=OC=x+1，y与x之间的关系是y=x+115.（1）证明：ABCD，AB=CD，四边形ABCD是平行四边形，AC平分BAD，BAC=DAC，ABCD，BAC=ACD，DAC=ACD，AD=DC，四边形ABCD是菱形（2）证明：如图1中，连接AE四边形ABCD是菱形，AB=AD，BO=OD，ACBD，FOD=90，ABD旋转得到EFD，BDF=ADE，AD=DE，BD=DF，点F恰好在AC上，DF=2OD，在RtFOD中，cosODF= = ，ADE=BD
11、F=60，ADE是等边三角形，EAD=60，MAD=30，EAM=EADMAD=30，EAM=MAD，DM=EM（3）解：如图2中，作EHDFAB=AD=15，ABD的周长为48，BD=481515=18，当DFBC时，PNF是直角三角形，在RtCOB中，OC= =12， BDOC= BCDP，DP= ，DF=BD=18，PF=18 = ，PNEH， = ， = ，PN= ，SPNF= = 故答案为 16.解：逆命题：有一条边上的高线和这条边的对角平分线重合的三角形是等腰三角形这个命题是真命题.已知：如图，在ABC中，ADBC,且AD平分BAC.求证：三角形ABC是等腰三角形证明：ADBC B
12、DA=CDA,AD平分BA,DAB=DAC,在ABD和ACD中，ABDACD(ASA)AB=AC,ABC是等腰三角形 17.（1）证明：ABC是等腰三角形，AB=BC，A=C，将等腰ABC绕顶点B逆时针方向旋转度到A1B1C1的位置，A1B=AB=BC，A=A1=C，A1BD=CBC1 ， 在BCF与BA1D中，BCFBA1D（2）解：四边形A1BCE是菱形，将等腰ABC绕顶点B逆时针方向旋转度到A1B1C1的位置，A1=A，ADE=A1DB，AED=A1BD=，DEC=180，C=，A1=，ABC=360A1CA1EC=180，A1=C，A1BC=AEC，四边形A1BCE是平行四边形，A1B=BC，四边形A1BCE是菱形
