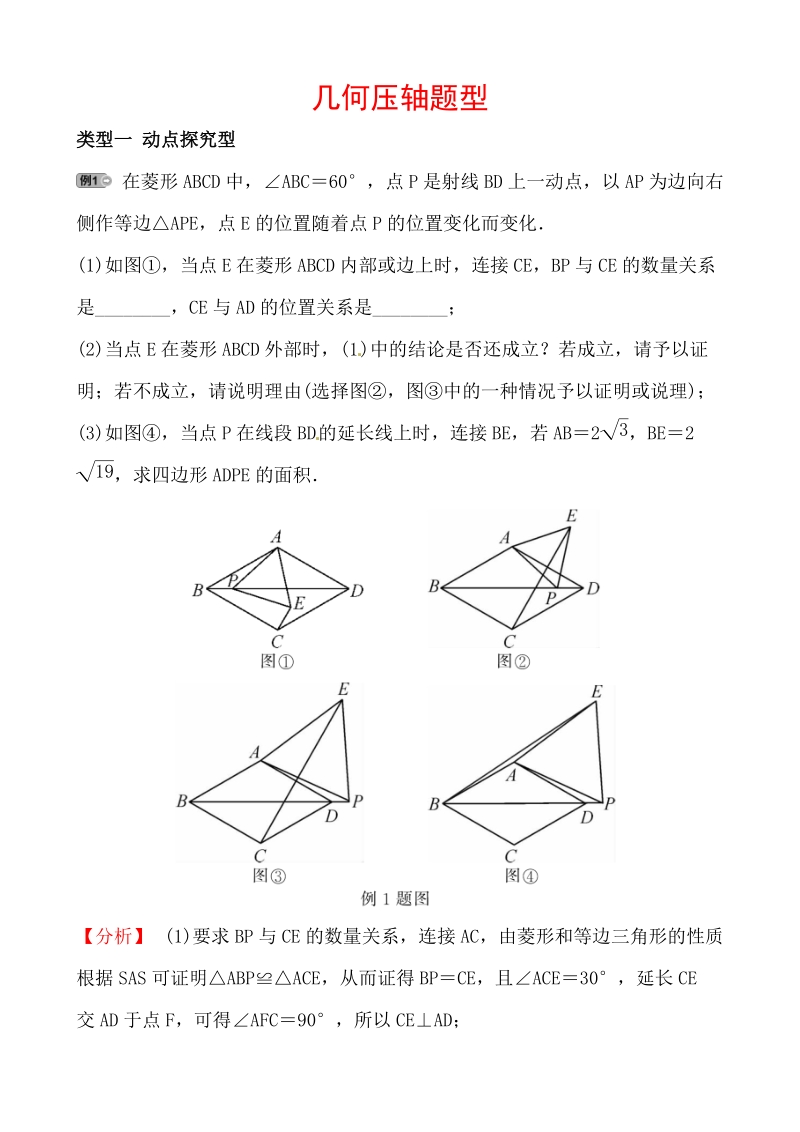
1、几何压轴题型类型一 动点探究型 在菱形ABCD中，ABC60，点P是射线BD上一动点，以AP为边向右侧作等边APE，点E的位置随着点P的位置变化而变化(1)如图，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是_，CE与AD的位置关系是_；(2)当点E在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由(选择图，图中的一种情况予以证明或说理)；(3)如图，当点P在线段BD的延长线上时，连接BE，若AB2，BE2，求四边形ADPE的面积【分析】 (1)要求BP与CE的数量关系，连接AC，由菱形和等边三角形的性质根据SAS可证明ABPACE，从
2、而证得BPCE，且ACE30，延长CE交AD于点F，可得AFC90，所以CEAD；(2)无论选择图还是图，结论不变，思路和方法与(1)一致；(3)要求四边形ADPE的面积，观察发现不是特殊四边形，想到割补法，分成钝角ADP和正APE，分别求三角形的面积，相加即可【自主解答】 解：(1)BPCE；CEAD；(2)选图，仍然成立，证明如下：如解图，连接AC交BD于点O，设CE交AD于点H.在菱形ABCD中，ABC60，BABC，例1题解图ABC为等边三角形，BACA.APE为等边三角形，APAE，PAEBAC60，BAPCAE.在BAP和CAE中，例1题解图BAPCAE(SAS)，BPCE，ACE
3、ABP30.AC和BD为菱形的对角线，CAD60，AHC90，即CEAD.选图，仍然成立，证明如下：如解图，连接AC交BD于点O，设CE交AD于点H，同理得BAPCAE(SAS)，BPCE，CEAD.(3)如解图，连接AC交BD于点O，连接CE交AD于点H，由(2)可知，CEAD，CEBP.在菱形ABCD中，ADBC，ECBC.BCAB2，BE2，在RtBCE中，CE8，例1题解图BPCE8.AC与BD是菱形的对角线，ABDABC30，ACBD，BD2BO2ABcos 306，AOAB，DPBPBD862，OPODDP5.在RtAOP中，AP2，S四边形ADPESADPSAPEDPAOAP22
4、(2)28.【难点突破】 本题的难点：一是如何找到全等的三角形，根据含60内角菱形的特点，连接AC是解决问题的关键；二是点P是动点，当它运动到菱形的外部时，在其运动过程中由“手拉手”模型找全等三角形；三是求不规则四边形的面积，要想到运用割补法，将四边形分解成两个三角形求解点拔 几何压轴题中的“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题在变化中找到不变的性质是解决数学“动点”探究题的基本思路，这也是动态几何数学问题中最核心的数学本质1已知，ABC是等腰三角形，CACB，0ACB90，点M在边
5、AC上，点N在边BC上(点M、点N不与所在线段端点重合)，BNAM，连接AN，BM.射线AGBC，延长BM交射线AG于点D，点E在直线AN上，且AEDE.(1)如图，当ACB90时：求证：BCMACN；求BDE的度数；(2)当ACB，其他条件不变时，BDE的度数是_；(用含的代数式表示)(3)若ABC是等边三角形，AB3，点N是BC边上的三等分点，直线ED与直线BC交于点F，请直接写出线段CF的长2在RtABC中，ACB90，AC12.点D在直线CB上，以CA，CD为边作矩形ACDE，直线AB与直线CE，DE的交点分别为F，G.(1)如图，点D在线段CB上，四边形ACDE是正方形若点G为DE中
6、点，求FG的长；第2题图若DGGF，求BC的长；(2)已知BC9，是否存在点D，使得DFG是等腰三角形？若存在，求该三角形的腰长；若不存在，试说明理由类型二 新定义型我们定义：如图，在ABC中，把AB绕点A顺时针旋转(0180)得到AB，把AC绕点A逆时针旋转得到AC，连接BC.当180时，我们称ABC是ABC的“旋补三角形”，ABC边BC上的中线AD叫做ABC的“旋补中线”，点A叫做“旋补中心”特例感知(1)在图，图中，ABC是ABC的“旋补三角形”，AD是ABC的“旋补中线”如图，当ABC为等边三角形时，AD与BC的数量关系为AD_BC；如图，当BAC90，BC8时，则AD长为_猜想论证(
7、2)在图中，当ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明拓展应用(3)如图，在四边形ABCD中，C90，D150，BC12，CD2，DA6.在四边形内部是否存在点P，使PDC是PAB的“旋补三角形”？若存在，给予证明，并求PAB的“旋补中线”长；若不存在，说明理由【分析】 (1)证明ADB是含有30角的直角三角形，则可得ADABBC；先证明BACBAC，根据直角三角形斜边上的中线等于斜边的一半即可；(2)结论：ADBC.如解图中，延长AD到点M，使得ADDM，连接BM，CM，先证明四边形ACMB是平行四边形，再证明BACABM，即可解决问题；(3)存在如解图中，延长AD交BC的
8、延长线于点M，作BEAD于点E，作线段BC的垂直平分线交BE于点P，交BC于点F，连接PA，PD，PC，作PCD的中线PN，连接DF交PC于点O.先证明PAPD，PBPC，再证明APDBPC180即可【自主解答】 解：(1)；【解法提示】 ABC是等边三角形，ABBCABABAC.DBDC，ADBC.180，BACBAC180，BAC60，BAC120，BC30，ADABBC.4；【解法提示】 180，BACBAC180.BAC90，BACBAC90.ABAB，ACAC，BACBAC(SAS)，BCBC.BDDC，ADBCBC4.(2)结论：ADBC.证明：如解图中，延长AD到点M，使得ADD
9、M，连接BM，CM.例2题解图BDDC，ADDM，四边形ACMB是平行四边形，ACBMAC.180，BACBAC180.BACABM180，BACMBA.ABAB，BACABM(SAS)，BCAM，ADBC.(3)存在证明：如解图中，延长AD交BC的延长线于点M，作BEAD于点E，作线段BC的垂直平分线交BE于点P，交BC于点F，连接PA，PD，PC，作PCD的中线PN，连接DF交PC于点O.例2题解图ADC150，MDC30，在RtDCM中，CD2，DCM90，MDC30，CM2，DM4，M60.在RtBEM中，BEM90，BM14，MBE30，EMBM7，DEEMDM3.AD6，AEDE.
10、BEAD，PAPD.PF垂直平分BC，PBPC.在RtCDF中，CD2，CF6，tanCDF，CDF60CPF.易证FCPCFD，CDPF.CDPF，四边形CDPF是平行四边形DCF90.四边形CDPF是矩形，CDP90，ADPADCCDP60，ADP是等边三角形BPFCPF60，BPC120，APDBPC180，PDC是PAB的“旋补三角形”在RtPDN中，PDN90，PDAD6，DN，PN.【难点突破】 第(3)问根据新定义判断点P的存在性是本题难点，但运用“直角三角形中30的角所对的直角边是斜边的一半”的性质以及三角形全等添加合适辅助线即可求解点拔 解决这类问题，首先要理解新定义的含义及
11、实质；其次要注意，在证明线段、角度相等或某个特殊图形时，主要应用全等，在计算线段的长或图形的周长、面积时，常注意运用相似、勾股定理及图形面积公式等1联想三角形外心的概念，我们可引入如下概念定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心举例：如图，若PAPB，则点P为ABC的准外心求解：(1)如图，CD为等边ABC的高，准外心P在高CD上，且PDAB，求APB的度数；(2)已知ABC为直角三角形，斜边BC5，AB3，准外心P在AC边上，求PA的长2如图，在ABC中，过顶点A作直线与对边BC相交于点D，两交点之间的线段把这个三角形分成两个图形若其中有一个图形与原三角形相似，则把这条线段
12、叫做这个三角形的“顶似线”(1)等腰直角三角形的“顶似线”的条数为_；(2)如图，在ABC中，ABAC，A36，BD是ABC的角平分线，求证：BD是ABC的“顶似线”；(3)如图，在ABC中，AB4，AC3，BC6，求ABC的“顶似线”的长3如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为这条边上的“奇特三角形”，这条边称为“奇特边”(1)如图，已知ABC是“奇特三角形”，ACBC，且C90.ABC的“奇特边”是_；设BCa，ACb，ABc，求abc；(2)如图，AM是ABC的中线，若ABC是BC边上的“奇特三角形”，找出BC2与AB2AC2之间的关系；(3)如图，在四边形ABCD
13、中，B90(ABBC)，BC2，对角线AC把它分成了两个“奇特三角形”，且ACD是以AC为腰的等腰三角形，求等腰ACD的底边长4如果三角形的两个内角与满足290，那么我们称这样的三角形为“准互余三角形”(1)若ABC是“准互余三角形”，C90，A60，则B_；(2)如图，在RtABC中，ACB90，AC4，BC5.若AD是BAC的平分线，不难证明ABD是“准互余三角形”试问在边BC上是否存在点E(异于点D)，使得ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由(3)如图，在四边形ABCD中，AB7，CD12，BDCD，ABD2BCD，且ABC是“准互余三角形”，求对角线
14、AC的长类型三 操作探究型 【操作发现】如图，在边长为1个单位长度的小正方形组成的网格中，ABC的三个顶点均在格点上(1)请按要求画图：将ABC绕点A按顺时针方向旋转90，点B的对应点为B，点C的对应点为C，连接BB；(2)在(1)所画图形中，ABB_【问题解决】如图，在等边三角形ABC中，AC7，点P在ABC内，且APC90，BPC120，求APC的面积小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将APC绕点A按顺时针方向旋转60，得到APB，连接PP，寻找PA，PB，PC三条线段之间的数量关系；想法二：将APB绕点A按逆时针方向旋转60，得到APC，连接PP，寻找PA，
15、PB，PC三条线段之间的数量关系请参考小明同学的想法，完成该问题的解答过程(一种方法即可)【灵活运用】如图，在四边形ABCD中，AEBC，垂足为E，BAEADC，BECE2，CD5，ADkAB(k为常数)，求BD的长(用含k的式子表示)【分析】 【操作发现】(1)先找到点B，C的对应点B，C，再连接构成三角形即可；(2)求ABB的度数可先判断ABB是等腰直角三角形，再求角度；【问题解决】根据两种不同的想法，选择其中一个进行证明；【灵活运用】需将ABD绕点A旋转得到ACG，再证明CDG90即可【自主解答】 解：【操作发现】(1)如解图所示，ABC即为所求；(2)45.【解法提示】 连接BB.AB
16、C是由ABC绕点A按顺时针方向旋转90得到的，ABAB，BAB90，ABB45.【问题解决】如解图，将APB绕点A按逆时针方向旋转60，得到APC，APP是等边三角形，APCAPB36090120150，例3题图PPAP，APPAPP60，PPC90，PPC30，PPPC，即APPC.APC90，AP2PC2AC2，即(PC)2PC272，PC2，AP，SAPCAPPC7；【灵活运用】如解图，连接AC.AEBC，BEEC，ABAC，将ABD绕点A逆时针旋转使得AB与AC重合，点D的对应点为G，连接DG.则BDCG.例3题解图BADCAG，BACDAG.ABAC，ADAG，ABCACBADGAG
17、D，ABCADG.ADkAB，DGkBC4k.BAEABC90，BAEADC，ADGADC90，GDC90，CG.BDCG.【难点突破】 在【灵活运用】一问中，要确定BD与k的数量关系，关键在于旋转ABD，使得AB与AC重合，从而证明CDG90，构造直角三角形是解决本题的难点，也是解决问题的突破口点拔 对于操作探究问题，首先掌握图形变换的性质，如图形的折叠：折痕为对称轴，有折痕就有角平分线，有折痕就有垂直平分等；图形的平移：有平移就有平行；图形的旋转：旋转前后图形全等，对应边相等，对应角相等；对应点与旋转中心的连线所成的角为旋转角，有旋转就有等腰三角形；其次注意运用全等证明线段相等，利用勾股定
18、理或相似求线段的长1在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EFAB.(1)若四边形ABCD为正方形如图，请直接写出AE与DF的数量关系_；将EBF绕点B逆时针旋转到图所示的位置，连接AE，DF，猜想AE与DF的数量关系，并说明理由(2)若四边形ABCD为矩形，BCmAB，其他条件都不变如图，猜想AE与DF的数量关系，并说明理由；将EBF绕点B逆时针旋转(090)得到EBF，连接AE，DF，请在图中画出草图，并直接写出AE和DF的数量关系2(1)操作发现：如图，小明画了一个等腰三角形ABC，其中ABAC，在ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形AB
19、D，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN.小明发现了：线段GM与GN的数量关系是_；位置关系是_(2)类比思考：如图，小明在此基础上进行了深入思考把等腰三角形ABC换为一般的锐角三角形，其中ABAC，其他条件不变，小明发现的上述结论还成立吗？请说明理由(3)深入研究：如图，小明在(2)的基础上，又作了进一步的探究向ABC的内侧分别作等腰直角三角形ABD，ACE，其他条件不变，试判断GMN的形状，并给予证明3如图，AM是ABC的中线，D是线段AM上一点(不与点A重合)，DEAB交AC于点F，CEAM，连接AE.(1)如图，当点D与点M重合时，求证：四边形ABDE是平行四
20、边形；(2)如图，当点D不与点M重合时，(1)中的结论还成立吗？请说明理由(3)如图，延长BD交AC于点H，若BHAC，且BHAM.求CAM的度数；当FH，DM4时，求DH的长参考答案类型一1解：(1)CACB，BNAM，CBBNCAAM，CNCM，ACBACB，BCCA，BCMACN.解：BCMACN，MBCNAC.EAED，EADEDA.AGBC，GACACB90，ADBDBC，ADBNAC，ADBEDANACEAD，ADBEDA1809090；BDE90.(2)或180；(3)4或.2解：(1)在正方形ACDE中，DGGE6，在RtAEG中，AG6.EGAC，ACFGEF，FGAG2.第
21、2题解图如解图，在正方形ACDE中，AEED，AEFDEF45.EFEF，AEFDEF，12，设12x.AEBC，B1x.GFGD，32x，在DBF中，3FDBB180，x(x90)x180，解得x30，B30，在RtABC中，BC12.(2)在RtABC中，AB15，如解图，当点D在线段BC上时，此时只有GFGD.第2题解图DGAC，BDGBCA，设BD3x，则DG4x，BG5x，AECD93x，GFGD4x，则AF159x.AECB，AEFBCF，整理得x26x50，解得x1或5(舍去)，腰长GD为4.如解图，当点D在线段BC的延长线上，且直线AB，CE的交点在AE上方时，此时只有GFDG
22、，设AE3x，则EG4x，AG5x，第2题解图FGDG124x.AEBC，AEFBCF，解得x2或2(舍去)，腰长DG为20.如解图，当点D在线段BC的延长线上，且直线AB，EC的交点在BD下方时，此时只有DFDG，过点D作DHFG于点H.第2题解图设AE3x，则EG4x，AG5x，DG4x12，FHGHDGcosDGB(4x12)，GF2GH，AFGFAG.ACDG，ACFGEF，解得x或(舍去)，腰长GD为，如解图，当点D在线段CB的延长线上时，此时只有DFDG，过点D作DHAG于点H.设AE3x，则EG4x，AG5x，DG4x12，FHGHDGcosDGB，第2题解图FG2FH，AFAG
23、FG.ACEG，ACFGEF，解得x或(舍去)，腰长DG为.综上所述，等腰三角形DFG的腰长为4或20或或.类型二1解：(1)如解图，若PBPC，连接PB，则PCBPBC.CD为等边三角形的高，ADBD，PCB30，PBDPBC30，PDDBAB，与已知PDAB矛盾，PBPC；若PAPC，连接PA，同理可得PAPC；若PAPB，由PDAB，得PDAD，APD45，故APB90.(2)BC5，AB3，BAC90，AC4.若PBPC，设PAx，则PCPB4x，x232(4x)2，x，即PA；若PAPC，则PA2；若PAPB，由解图知，在RtPAB中，不可能存在综上所述，PA的长为2或.2(1)解：
24、1.(2)证明： ABAC，A36，ABCACB72.BD是ABC的角平分线，ABDDBC36，ACBD.又CC，ABCBDC，BD是ABC的“顶似线”(3)解：如解图，当ADCBAC时，AD为ABC的“顶似线”，则，即，AD2；如解图，当ADCACB时，CD为ABC的“顶似线”，则，即，CD；过顶点B的“顶似线”不存在综上所述，ABC的“顶似线”的长为2或.3解：(1)AC；如解图，过点B作AC边上的中线BE，则BEACb，CEAEb.在RtABC中，a2b2c2，在RtBCE中，a2(b)2b2.解得ab，cb.abc2.(2)如解图，过点A作AFBC于点F，则AFBAFC90.设AMBC
25、a，AFh，MFx，则BMCMa.在RtABF中，AB2BF2AF2(x)2h2，在RtACF中，AC2CF2AF2(x)2h2，AB2AC22x22h2.在RtAMF中，AM2MF2AF2，即a2x2h2.AB2AC2BC2.(3)B90，BCAB，BC为ABC的“奇特边”BC2，由(1)知ABBC，ACBC7.设等腰ACD的底边长为y，由(2)中结论知：当腰为“奇特边”时，有72y272，解得y(负值已舍去)当底边为“奇特边”时，有7272y2，解得y(负值已舍去)等腰ACD的底边长为或.4解：(1)C90，A60，60，15，B15.(2)若存在一点E，使得ABE也是“准互余三角形”，则
26、2EBAEAB90.如解图，作射线BF，使得FBEABE，延长AE交BF于点F，则BFE90.即BE为FBA的角平分线，过点E作EGAB于点G，则EGEF，可得BEFBEG.又BEGBAC，BEFBAC，.又BEFAEC，由可得，BE1.8.(3)如解图，将BCD沿BC翻折得BCE，则CECD12，ABD2BCDDCE，DCEDBE180，即ABDDBE180，点A，B，E共线，易知2ACBBAC90不成立，存在2BACACB90，易证得ECBEAC，即，解得BE9(负值已舍去)，AE16，在RtAEC中，利用勾股定理得，AC20.类型三1解：(1)DFAE；DFAE；理由：EBFABD45，
27、ABEFBD.，ABEDBF，DFAE.(2)如解图，过点F作FGAD于点G，则四边形AEFG是矩形，GFAE.tanFDG，ADBCmAB，DGmGF，在RtDGF中，由勾股定理得DFGF，DFAE.画出草图如解图，DFAE.2解：(1)GMGN；GMGN.【解法提示】 如解图，连接BE，CD相交于点H.ABD和ACE都是等腰直角三角形，ABAD，ACAE，BADCAE90CADBAE，ACDAEB(SAS)，CDBE，ADCABE，BDCDBHBDCABDABEBDCABDADCADBABD90，BHD90，CDBE.点M，G分别是BD，BC的中点，MGCD.同理：NG BE，MGNG，M
28、GNG.(2)小明发现的上述结论成立理由：如解图，连接CD，BE相交于点H.DABCAE90，DACBAE.DABA，CAEA，DACBAE(SAS)，FBHADF，DCBE.M是BD的中点，G是BC的中点，MGDC，同理NGBE，MGNG.设CD交AB于点F，则FHB180(FBHBFH)180(ADFAFD)90，CDBE，MGNG；(3)GMN为等腰直角三角形证明：如解图，连接EB，DC，延长线相交于点H，同(1)的方法得，MGNG，同(1)的方法得，ABEADC，AEBACD，CEHECHAEHAEC180ACDACEACD45180ACD4590，DHE90，同(1)的方法得，MGN
29、G.3(1)证明： DEAB，EDCABM.CEAM，ECDADB.AM是ABC的中线，且点D与点M重合，BDDC，ABDEDC(ASA)，ABED.ABED，四边形ABDE是平行四边形(2)解：结论成立理由如下：第3题解图如解图，过点M作MGDE交CE于点G.CEAM，四边形DMGE是平行四边形，EDGM，且EDGM.ABDE，ABGM，ABMGMC.AMCE，AMBGCM.AM为ABC的中线，BMMC.ABMGMC(ASA)，ABGM，ABDE.ABDE，四边形ABDE是平行四边形(3)解：如解图，取线段HC的中点I，连接MI，第3题解图BMMC，MI是BHC的中位线，MIBH，MIBH.BHAC，且BHAM.MIAM，MIAC，CAM30.设DHx，则AHx，AD2x，AM42x，BH42x.四边形ABDE是平行四边形，DFAB，解得x1或x1(舍去)，DH1.
