1、2018-2019学年江苏省泰州市高一（上）期末数学试卷一、填空题（本大题共14小题，每小题5分，共计70分不需要写出解答过程，请将答案填写在答题卡相应的位置上）1（5分）已知集合A0，1，2，3，B1，0，1，则AB 2（5分）如果角始边为x轴的正半轴，终边经过点（2，），那么tan 3（5分）已知（2，3），（x，1），若，则实数x 4（5分）若幂函数yx（R）的图象过点（2，），则 5（5分）函数f（x）lg（2x4）的定义域为 6（5分）将函数ysinx的图象上所有点的纵坐标保持不变，横坐标变为原来的倍，所得到的图象的函数解析式为 7（5分）已知函数，则 8（5分）设a0.32，b20
2、.3，c2，则a，b，c的大小关系为 （用“”号连结）9（5分）已知|1，|2，60，则|2| 10（5分）函数f（x）Asin（x+）（A0，0，0）的部分图象如图所示，则f（0）的值为 11（5分）计算： 12（5分）已知函数若，则 13（5分）在ABC中，D为AC的中点，4，则 14（5分）已知函数，若当x1，x21，3时，都有f（x1）2f（x2），则a的取值范围为 二、解答题（本大题共6小题，共计90分请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤）15（14分）已知集合A1，3，B2，2（1）求AB，AB；（2）若Aa，+），求实数a的取值范围16（14分）已知，
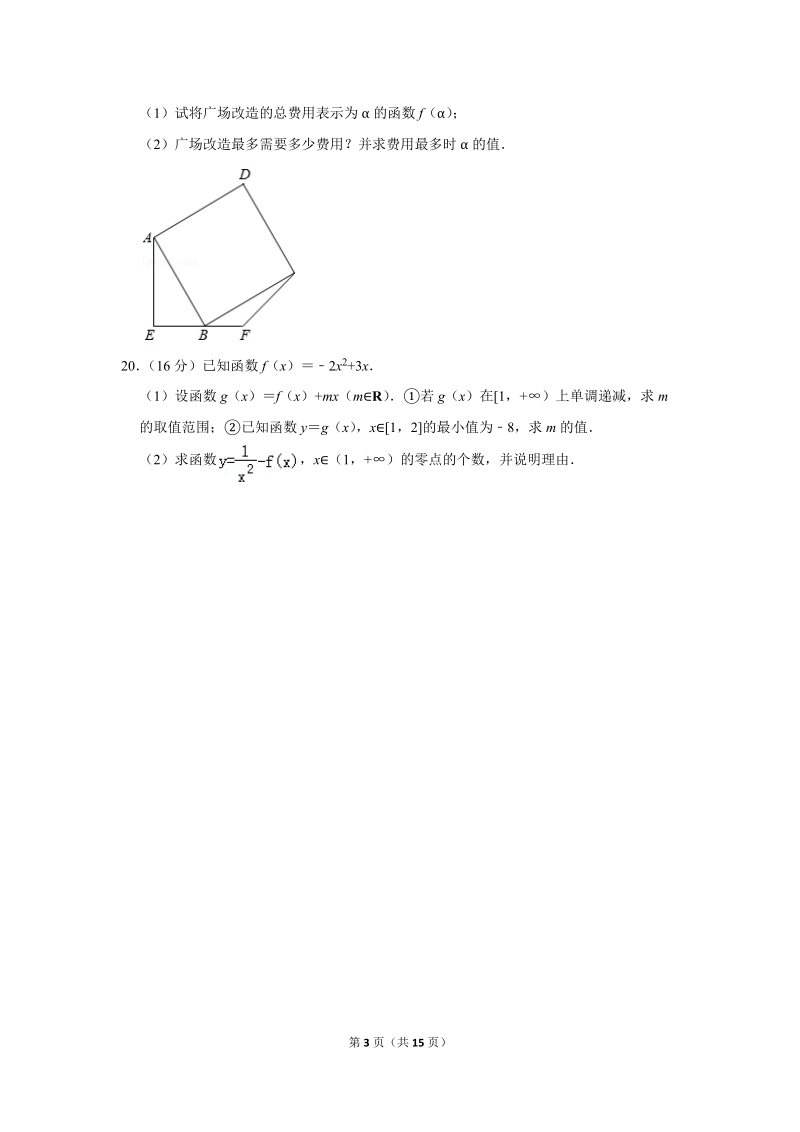
3、（，），（，）（1）求cos（+）的值；（2）求tan2的值17（14分）如图，在梯形ABCD中，ABCD，ABAD，AB8，CD5，AD2（1）若，求实数，的值；（2）若，求实数的值18（16分）已知f（x）是定义在R上的奇函数，当x0时，f（x）2x1（1）求f（0）的值；（2）当x0时，求f（x）的解析式；（3）若关于x的方程f（2x）+bf（x）+b+30（bR）在（0，1）上有两个不相等的实根，求b的取值范围19（16分）如图，某市规划将边长为1百米的正方形广场ABCD扩建为五边形广场AEFCD，点B在EF上，AEEF，且AEEF其中ABE和BCF区域种植草坪，每平方百米草坪的造价为
4、200万元；沿EB建浮雕，浮雕的总造价W1（单位：万元）与EB的长度（单位：百米）的平方成正比，比例系数为100；沿BF建电子显示屏，电子显示屏的总造价W2（单位：万元）与BF的长度（单位：百米）成正比，比例系数为设BAE，（0，）（1）试将广场改造的总费用表示为的函数f（）；（2）广场改造最多需要多少费用？并求费用最多时的值20（16分）已知函数f（x）2x2+3x（1）设函数g（x）f（x）+mx（mR）若g（x）在1，+）上单调递减，求m的取值范围；已知函数yg（x），x1，2的最小值为8，求m的值（2）求函数，x（1，+）的零点的个数，并说明理由2018-2019学年江苏省泰州市高一（
5、上）期末数学试卷参考答案与试题解析一、填空题（本大题共14小题，每小题5分，共计70分不需要写出解答过程，请将答案填写在答题卡相应的位置上）1（5分）已知集合A0，1，2，3，B1，0，1，则AB0，1【分析】利用交集定义直接求解【解答】解：集合A0，1，2，3，B1，0，1，AB0，1故答案为：0，1【点评】本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用2（5分）如果角始边为x轴的正半轴，终边经过点（2，），那么tan【分析】依据任意角的三角函数的定义求出tan的值，【解答】解：角始边为x轴的正半轴，终边经过点（2，），tan，故答案为：【点评】本题考查任意角的三角函
6、数的定义，属于基础题3（5分）已知（2，3），（x，1），若，则实数x【分析】根据即可得出23x0，解出x即可【解答】解：；23x0；故答案为：【点评】考查向量坐标的定义，向量平行时的坐标关系4（5分）若幂函数yx（R）的图象过点（2，），则【分析】利用待定系数法求出的值【解答】解：幂函数yx（R）的图象过点（2，），则2，解得，故答为：【点评】本题考查了幂函数的定义与应用问题，是基础题目5（5分）函数f（x）lg（2x4）的定义域为x|x2【分析】根据对数函数的性质建立不等式即可求出函数的定义域【解答】解：要使函数有意义，则2x40，解得x2，函数的定义域为x|x2，故答案为：x|x2【点评
7、】本题主要考查函数定义域的求法，根据函数成立的条件是解决本题的关键，比较基础6（5分）将函数ysinx的图象上所有点的纵坐标保持不变，横坐标变为原来的倍，所得到的图象的函数解析式为ysin2x【分析】直接利用函数的图象的平移变换和伸缩变换的应用求出结果【解答】解：函数ysinx的图象上所有点的纵坐标保持不变，横坐标变为原来的倍，所得到的图象的函数解析式为ysin2x，故答案为：ysin2x【点评】本题考查的知识要点：函数图象的平移变换和伸缩变换的应用，主要考查学生的运算能力和转化能力，属于基础题型7（5分）已知函数，则【分析】根据分段函数的表达式，利用代入法进行求解即可【解答】解：由分段函数得
8、f（）（）21，则f（）（），f（f（）f（），故答案为：【点评】本题主要考查函数值的计算，利用代入法是解决本题的关键比较基础8（5分）设a0.32，b20.3，c2，则a，b，c的大小关系为abc（用“”号连结）【分析】利用指数函数与对数函数的单调性即可得出【解答】解：0a0.321，2b20.31，c22，abcabc故答案为：abc【点评】本题考查了指数函数与对数函数的单调性，属于基础题9（5分）已知|1，|2，60，则|2|【分析】利用数量积运算法则及其向量的模的平方与向量的平方相等的性质即可得出【解答】解：，；故答案为：【点评】本题考查了向量的数量积公式以及向量的模的平方与向量的平方
9、相等的性质的运用；属于基础题10（5分）函数f（x）Asin（x+）（A0，0，0）的部分图象如图所示，则f（0）的值为【分析】从图象中可以得出A，利用周期公式可求2，代入点，解得：2k，kZ，结合范围0，可求，即可计算得解f（0）的值【解答】（本题满分为8分）解：从图象中可以得出，A2，周期为，从而可得T，得2，（2分）故f（x）2sin（2x+），（4分）代入点，可得：2，+2k+，kZ，解得：2k，kZ，0，k0时，可得：，（6分）f（x）2sin（2x），（7分）f（0）2sin（）（8分）故答案为：【点评】本题主要考查由函数yAsin（x+）的部分图象求解析式，正弦函数的性质，考查了
10、转化思想和数形结合思想的应用，属于中档题11（5分）计算：5【分析】直接利用有理指数幂的运算性质与对数的运算性质化简求值【解答】解：2+35故答案为：5【点评】本题考查有理指数幂的运算性质与对数的运算性质，是基础的计算题12（5分）已知函数若，则【分析】由已知求得，再由cos（+）cos2（），展开倍角公式求解【解答】解：由，得，cos（+）cos2（）故答案为：【点评】本题考查三角函数的恒等变换及化简求值，考查倍角公式及诱导公式的应用，是基础题13（5分）在ABC中，D为AC的中点，4，则9【分析】用表示出各向量，根据，得出与，的关系，根据4列方程求出答案【解答】解：D为AC的中点，（）（）
11、+4，（）6，（）3，6+，3+，（6+）（3+）+4，即0，9故答案为：9【点评】本题考查了平面向量的基本定理，数量积运算，属于中档题14（5分）已知函数，若当x1，x21，3时，都有f（x1）2f（x2），则a的取值范围为（，13，15）【分析】把问题转化为f（x）在1，3上的最大值与最小值的比小于2，如果对a分类求出函数的最值，进一步求解a的范围【解答】解：由，x1，x21，3时，f（x1）0，f（x2）0，当x1，x21，3时，都有f（x1）2f（x2），即2，也就是f（x）在1，3上的最大值与最小值的比小于2当0a1时，f（x）在1，3上为增函数，则22，解得：a1；当a3时，f（x
12、）在1，3上为减函数，则22，解得：3a15；当1a3时，由f（x），可知f（x）在1，）上为减函数，在（，3上为增函数f（x）maxmaxf（1），f（3）由f（1）f（3），得1+a3+，解得a3，则22，此时a综上，a的取值范围为（，13，15）故答案为：（，13，15）【点评】本题考查利用导数研究函数的单调性，考查分类讨论的数学思想方法，是中档题二、解答题（本大题共6小题，共计90分请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤）15（14分）已知集合A1，3，B2，2（1）求AB，AB；（2）若Aa，+），求实数a的取值范围【分析】（1）进行交集、并集的运算即可；（
13、2）根据Aa，+）即可得出a1，即得出a的取值范围【解答】解：（1）A1，3，B2，2；AB1，2，AB2，3；（2）Aa，+）；a1；实数a的取值范围为（，1【点评】考查区间表示集合的概念，子集的定义，以及交集、并集的运算16（14分）已知，（，），（，）（1）求cos（+）的值；（2）求tan2的值【分析】（1）根据同角三角函数关系结合两角和差的余弦公式进行求解即可；（2）结合正切函数的倍角公式进行求解【解答】解：（1），（，），（，）cos，sin，则cos（+）coscossinsin（）（）（2）tan，则tan2【点评】本题主要考查三角函数值的求解，利用两角和差的余弦公式以及边角公
14、式同角的三角函数关系是解决本题的关键17（14分）如图，在梯形ABCD中，ABCD，ABAD，AB8，CD5，AD2（1）若，求实数，的值；（2）若，求实数的值【分析】（1）根据条件可分别以AB，AD所在直线为x轴，y轴，建立平面直角坐标系，从而可得出A（0，0），B（8，0），D（0，2），C（5，2），从而可求出，根据即可建立关于，的方程组，解出，即可；（2）根据条件即可求出点E的坐标为（8，0），从而可求出，根据即可得出，进行数量积的坐标运算即可求出【解答】解：（1）分别以边AB，AD所在直线为x，y轴，建立如图所示平面直角坐标系，则：A（0，0），B（8，0），D（0，2），C（5，2
15、）；解得；（2）；E（8，0）；解得【点评】考查通过建立坐标系，利用坐标解决向量问题的方法，根据点的坐标求向量的坐标的方法，以及向量坐标的数乘和数量积运算，向量垂直的充要条件18（16分）已知f（x）是定义在R上的奇函数，当x0时，f（x）2x1（1）求f（0）的值；（2）当x0时，求f（x）的解析式；（3）若关于x的方程f（2x）+bf（x）+b+30（bR）在（0，1）上有两个不相等的实根，求b的取值范围【分析】（1）根据函数奇偶性的性质进行求解即可（2）根据奇函数的对称性进行转化求解即可（3）将方程进行化简，利用换元法转化为一元二次方程，根据根的分布进行求解即可【解答】解：（1）f（x）
16、是定义在R上的奇函数，f（0）0（2）若x0，则x0，当x0时，f（x）2x1，当x0时，f（x）2x1f（x），则f（x）2x+1，x0（3）当0x1时，方程f（2x）+bf（x）+b+30等价为22x1+b（2x1）+b+30，即（2x）2+b2x+20，设t2x，0x1，1t2，即方程t2+bt+20在1t2上有两个不相等的实根，设f（t）t2+bt+2，f（0）20，要使t2+bt+20在1t2上上有两个不相等的实根，则，即，即3b，即实数b的取值范围是3b【点评】本题主要考查函数奇偶性的应用，以及一元二次方程根的分布，利用换元法将方程转化为一元二次方程是解决本题的关键19（16分）如
17、图，某市规划将边长为1百米的正方形广场ABCD扩建为五边形广场AEFCD，点B在EF上，AEEF，且AEEF其中ABE和BCF区域种植草坪，每平方百米草坪的造价为200万元；沿EB建浮雕，浮雕的总造价W1（单位：万元）与EB的长度（单位：百米）的平方成正比，比例系数为100；沿BF建电子显示屏，电子显示屏的总造价W2（单位：万元）与BF的长度（单位：百米）成正比，比例系数为设BAE，（0，）（1）试将广场改造的总费用表示为的函数f（）；（2）广场改造最多需要多少费用？并求费用最多时的值【分析】（1）求出AE，BE，BF，CBF，根据题意得出f（）；（2）根据三角恒等变换和换元法求出f（）的最大
18、值【解答】解：（1）BEABsinBAEsin，EFAEABcosBAEcos，BFEFBEcossin，SABE，又CBFABCABE（），BC1，SBCF，f（）200（+）+100sin2+100（cossin）200sincos+100（cossin），（0，）（2）令cossint，则sincos，f（）100t2+100t+100，又tcossincos（+），（0，）0t1100t2+100t+100100（t）2+150，当t时，f（）取得最大值150，此时cos（+），故广场改造费用最多需要150万元，费用最多时【点评】本体考查了解三角形，三角恒等变换与三角函数求值，属于中档
19、题20（16分）已知函数f（x）2x2+3x（1）设函数g（x）f（x）+mx（mR）若g（x）在1，+）上单调递减，求m的取值范围；已知函数yg（x），x1，2的最小值为8，求m的值（2）求函数，x（1，+）的零点的个数，并说明理由【分析】（1）考虑对称轴在区间的左边，解不等式可得m的范围；讨论对称轴和区间的关系，结合单调性可得最小值，进而得到m的值；（2）由题意可得yf（x）与y在x1的图象交点个数即为零点个数，画出图象，观察交点即可【解答】解：（1）函数g（x）f（x）+mx2x2+（3+m）x，g（x）在1，+）上单调递减，可得1，解得m1；g（x）的对称轴为x，当1，即m1，即g（x）在1，2递减，可得g（2）2+2m8，即m3成立；当2，即m5，即g（x）在1，2递增，可得g（1）1+m8，即m9不成立；当12，即1m5，g（x）的最小值为g（1）或g（2），若g（1）8，解得m9，此时g（2）218208，不成立；若g（2）8，解得m3，此时g（1）1328，不成立综上可得m3；（2）函数，x（1，+）的零点个数，即为yf（x）与y的图象交点个数，作出yf（x）与y在x1的图象，可得它们有1个交点，则零点个数为1【点评】本题考查二次函数的单调性和最值求法，注意运用对称轴和区间的关系，考查函数的零点个数问题，注意运用数形结合思想，考查运算能力，属于中档题
