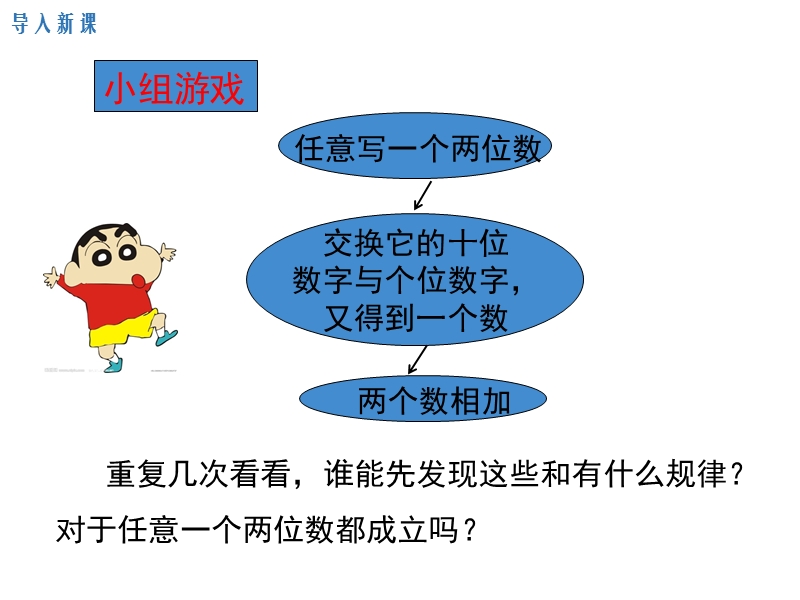
1、2.2 整式的加减,第二章 整式的加减,导入新课,讲授新课,当堂练习,课堂小结,第3课时 整式的加减,1.熟练进行整式的加减运算.(重点） 2.能根据题意列出式子，表示问题中的数量关系.（难点）,导入新课,小组游戏,重复几次看看，谁能先发现这些和有什么规律？对于任意一个两位数都成立吗？,10a+b+10b+a=11a+11b=11(a+b),讲授新课,合作探究,如果用a，b分别表示一个两位数的十位数字和个位数字，那么这个两位数可以表示为： .交换这个两位数的十位数字和个位数字，得到的数是： .将这两个数相加：,10a+b,10b+a,(10a+b),(10b+a),结论：,这些和都是11的倍数
2、.,+ _ =_ .,做一做,你又发现什么了规律？,原三位数728，百位与个位交换后的数为827,由728 827= 99.你能看出什么规律并验证它吗？,举例：,任意一个三位数可以表示成100a+10b+c,设原三位数为100a+10b+c，百位与个位交换后的数为100c+10b+a,它们的差为：,(100a+10b+c)( 100c+10b+a) = 100a+10b+c100c10ba =99a99c =99(ac),验证：,议一议,在上面的两个问题中，分别涉及了整式的什么运算？说说你是如何运算的？,去括号、合并同类项,八字诀,整式的加减运算,例1 计算：(1)(2a-3b)+(5a+4b
3、)；(2)(8a-7b)-(4a-5b),解： (1)(2a-3b)+(5a+4b),=2a-3b+5a+4b,=7a+b,去括号,合并同类项,=8a-7b-4a+5b,=4a-2b,(2)(8a-7b)-(4a-5b),去括号,合并同类项,典例精析,解：,有括号要先去括号,有同类项再合并同类项,结果中不能再有同类项,练一练：求上述两多项式的差.,答案： 12x2+5x+7,例2 求多项式 与 的和.,3.运算结果，常将多项式的某个字母（如x）的降幂（升幂）排列.,总结归纳,1.几个整式相加减，通常用括号把每一个整式括起来，再用加、减连接，然后进行运算,2.整式加减实际上就是： 去括号、合并同
4、类项.,例3 一种笔记本的单价是x元，圆珠笔的单价是y元.小红买这种笔记本3本，买圆珠笔2支；小明买这种笔记本4本，买圆珠笔3支.买这些笔记本和圆珠笔，小红和小明一共花费多少钱？,解：小红买笔记本和圆珠笔共花费（3x+2y）元，小明买笔记本和圆珠笔共花费（4x+3y）元.,小红和小明一共花费（单位：元）,（3x+2y）+（4x+3y）,=3x+2y+4x+3y,=7x+5y,你还能有其他解法吗？,另解：小红和小明买笔记本共花费（3x+4x）元，买圆珠笔共花费（2y+3y）元.,小红和小明一共花费（单位：元）,（3x+4x）+（2y+3y）,=7x+5y,分别计算笔记本和圆珠的花费.,例4 做大
5、小两个长方体纸盒，尺寸如下(单位：cm):（1）做这两个纸盒共用料多少平方厘米？,a,b,c,1.5a,2b,2c,（1）做这两个纸盒共用料（2ab+2bc+2ca）+（6ab+8bc+6ca）,=2ab+2bc+2ca+6ab+8bc+6ca,2ab,+2bc,+2ca,6ab,+8bc,+ 6ca,（2）做大纸盒比做小纸盒多用料,（6ab+8bc+6ca）-（2ab+2bc+2ca）,=6ab+8bc+6ca- 2ab-2bc-2ca,=4ab+6bc+4ca(cm ),2,（2）做大纸盒比小纸盒多用料多少平方厘米？,小纸盒的表面积是（2ab+2bc+2ca）cm 大纸盒的表面积是（6ab
6、+8bc+6ca）cm,2,2,整式加减解决实际问题的一般步骤： 根据题意列代数式； 去括号、合并同类项.； 得出最后结果.,总结归纳,例5 求,的值， 其中,先将式子化简，再代入数值进行计算,解：,当 时，,原式,去括号,合并同类项,将式子化简,能力提升,有这样一道题“当a2，b2时，求多项式3a3b3 a2bb（4a3b3 a2bb2）（a3b3 a2b）2b23的值”，马小虎做题时把a2错抄成a2，王小真没抄错题，但他们做出的结果却都一样，你知道这是怎么回事吗？说明理由.,解：将原多项式化简后，得b2b3.,因为这个式子的值与a的取值无关，所以即使把a抄错，最后的结果都会一样.,当堂练习
7、,2.长方形的一边长等于3a+2b,另一边比它大a-b,那么这个长方形的周长是（ ） A.14a+6b B.7a+3b C.10a+10b D.12a+8b,1.已知一个多项式与 的和等于 ，则这个多项式是（ ）,A,A,3.若A是一个二次二项式，B是一个五次五项式，则BA一定是（ ）A.二次多项式 B.三次多项式 C.五次三项式 D. 五次多项式,4.多项式 与多项式 的和不含二次项，则m为（ ）,A.2 B.-2 C.4 D.-4,D,C,5.已知 则,6.若mn=m+3，则2mn+3m-5mn+10=_.,-9a2+5a-4,1,7.计算,(1) ab3+2a3b a2bab3 a2ba
8、3b(2)(7m24mnn2)(2m2mn+2n2)(3)3(3x+2y)0.3(6y5x)(4)( a32a6) ( a34a7),答案：(1),8.某公司计划砌一个形状如下图（1）的喷水池，后有人建议改为如下图（2）的形状，且外圆直径不变，只是担心原来备好的材料不够，请你比较两种方案，哪一种需用的材料多（即比较两个图形的周长）？若将三个小圆改为n个小圆，又会得到什么结论？,思路点拨：,设大圆半径为R，小圆半径依次为r1，r2，r3， 则图（1）的周长为4R，图（2）的周长为 2R+2r1+2r2+2r3=2R+2（r1+r2+r3）， 因为2r1+2r2+2r3=2R，所以r1+r2+r3=R，因此图（2） 的周长为2R+2R=4R 这两种方案，用材料一样多，将三个小圆改为n个 小圆，用料还是一样多,R,2r1+2r2+2r3=2R,课堂小结,整式的加减,
