1、人教版2019-2020湖北省武汉市八中九年级数学上册期中考试试卷（120分）一、选择题（每小题3分，共30分）1.下列图案中，不是中心对称图形的是( ) A.B.C.D.2.如图，已知ABCD中，AEBC于点E，以点b为中心，取旋转角等于ABC，把BAE顺时针旋转，得到ABAE，连接DA若ADC=60，ADA=50，则DAE的大小为 ( ) A.130B.150C.160D.1703.一元二次方程(x+3)2=16可转化为两个一元一次方程，其中一个一元次方程是x+3=4，则另一个一元一次方程是（ ） A.x-3=-4B.x-3=4C.x+3=4D.x+3=-44.二次函数y=-x2+bx+4
2、经过(-2，n)（ 4,n）两点，则n 的值是（ ） A.-4B.-2C.2D.45.在平面直角坐标系中，P点关于原点的对称点为P1(-3，- 83 )，P点关于x轴的对称点为P2(a，b)，则 3ab = ( ) A.-2B.2C.4D.-46.设一元二次方程 x22x4=0 两个实根为x1和x2 ， 则下列结论正确的是（ ） A.x1+x2=2B.x1+x2=-4C.x1x2=2D.x1x2=47.武汉市企业退休人员王大爷2016年的工资是每月2100元，连续两年增长后，2018年大王大爷的工资是每月2541元，若设这两年平均每年的增长率为 x ，根据题意可列方程（ ） A.2100(1+
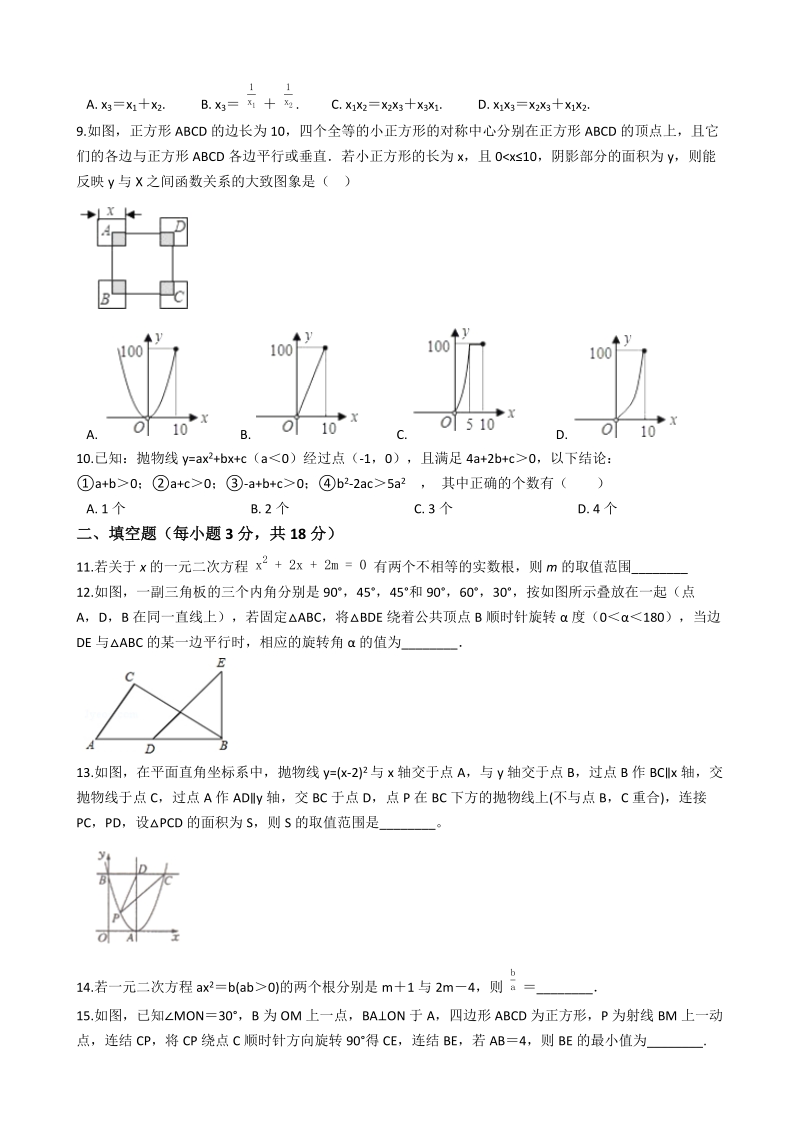
3、x)=2541B.2541(1x)2=2100C.2100(1+x)2=2541D.2541(1x2)=21008.设抛物线yax2(a0)与直线ykxb相交于两点，它们的横坐标为x1 ， x2 ， 而x3是直线与x轴交点的横坐标，那么x1 ， x2 ， x3的关系是（ ） A.x3x1x2.B.x3 1x1 1x2 .C.x1x2x2x3x3x1.D.x1x3x2x3x1x2.9.如图，正方形ABCD的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD的顶点上，且它们的各边与正方形ABCD各边平行或垂直若小正方形的长为x，且0x10，阴影部分的面积为y，则能反映y与X之间函数关系的
4、大致图象是（ ）A.B.C.D.10.已知：抛物线y=ax2+bx+c（a0）经过点（-1，0），且满足4a+2b+c0，以下结论：a+b0；a+c0；-a+b+c0；b2-2ac5a2 ， 其中正确的个数有（） A.1个B.2个C.3个D.4个二、填空题（每小题3分，共18分）11.若关于x的一元二次方程 x2+2x+2m=0 有两个不相等的实数根，则m的取值范围_ 12.如图，一副三角板的三个内角分别是90，45，45和90，60，30，按如图所示叠放在一起（点A，D，B在同一直线上），若固定ABC，将BDE绕着公共顶点B顺时针旋转度（0180），当边DE与ABC的某一边平行时，相应的旋转
5、角的值为_ 13.如图，在平面直角坐标系中，抛物线y=(x-2)2与x轴交于点A，与y轴交于点B，过点B作BCx轴，交抛物线于点C，过点A作ADy轴，交BC于点D，点P在BC下方的抛物线上(不与点B，C重合)，连接PC，PD，设PCD的面积为S，则S的取值范围是_。 14.若一元二次方程ax2b(ab0)的两个根分别是m1与2m4，则 ba _ 15.如图，已知MON30，B为OM上一点，BAON于A，四边形ABCD为正方形，P为射线BM上一动点，连结CP，将CP绕点C顺时针方向旋转90得CE，连结BE，若AB4，则BE的最小值为_. 16.如图，抛物线 y=x2+2x+m+1 （m为常数）交
6、y轴于点A，与x轴的一个交点在2和3之间，顶点为B 抛物线 y=x2+2x+m+1 与直线y=m+2有且只有一个交点；若点 M(2,y1) 点 N(12,y2) 、点 P(2,y3) 在该函数图象上，则 y1OC)的长分别是一元二次方程x2-14x+48=0的两个实数根 （1）求C点坐标； （2）求直线MN的解析式； （3）在直线MN上存在点P，使以P，B，C三点为顶点的三角形是等腰三角形请直接写出P点坐标 21.（8分）某公司研制出新产品，该产品的成本为每件2400元在试销期间，购买不超过10件时，每件销售价为3000元；购买超过10件时，每多购买一件，所购产品的销售单价均降低5元，但最低销
7、售单价为2600元。请解决下列问题： （1）直接写出：购买这种产品 _件时，销售单价恰好为2600元； （2）设购买这种产品x件(其中x10，且x为整数)，该公司所获利润为y元，求y与x之间的函数表达式； （3）该公司的销售人员发现：当购买产品的件数超过10件时，会出现随着数量的增多，公司所获利润反而减少这一情况为使购买数量越多，公司所获利润越大，公司应将最低销售单价调整为多少元？(其它销售条件不变) 22.（10分）如图，以矩形OABC的顶点O为坐标原点，OA所在直线为x轴，OC所在直线为y轴，建立平面直角坐标系，已知OA8，OC10，将矩形OABC绕点O逆时针方向旋转（0180）得到矩形O
8、DEF （1）当点E恰好落在y轴上时，如图1，求点E的坐标 （2）连结AC，当点D恰好落在对角线AC上时，如图2，连结EC，EO， 求证：ECDODC；求点E的坐标（3）在旋转过程中，点M是直线OD与直线BC的交点，点N是直线EF与直线BC的交点，若BM 12 BN，请直接写出点N的坐标 23.（10分）如图,二次函数y=-x2+bx+c与x轴交于点B和点A(1,0),与y轴交于点C(0,4),与一次函数y=x+a交于点A和点D. （1）求出a、b、c的值； （2）若直线AD上方的抛物线存在点E，可使得EAD面积最大，求点E的坐标； （3）点F为线段AD上的一个动点,点F到(2)中的点E的距离
9、与到y轴的距离之和记为d，求d的最小值及此时点F的坐标。 24.（12分）如图，已知抛物线y=ax2+bx+c经过A（3，0），B（1，0），C（0，3）三点，其顶点为D，对称轴是直线l，l与x轴交于点H. （1）求该抛物线的解析式； （2）若点P是该抛物线对称轴l上的一个动点，求PBC周长的最小值； （3）如图（2），若E是线段AD上的一个动点（ E与A.D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，ADF的面积为S. 求S与m的函数关系式；S是否存在最大值？若存在，求出最大值及此时点E的坐标； 若不存在，请说明理由.人教版2019-2020湖北省武汉
10、市八中九年级数学上册期中考试试卷一、选择题（30分）1.解：根据中心对称图形的概念，A、B、D是中心对称图形，故都不符合题意，只有C不是中心对称图形，符合题意。 故答案为：C。2.解：ABCD ADC=ABC=60，ADBC 以点B为中心，取旋转角等于ABC，把BAE顺时针旋转，得到ABAE， ABC=ABE=60 AEBE，ADBC AEB=DAE=AEB=90 BAE=90-60=30， 在四边形ADAE中 DAE=360-DAE-AEC- ADA=360-90-90-50=130 DAE= BAE+DAE=30+130=160 故答案为：C 3.解：（x+3）2=16 方程两边同时开平方
11、，得 x+3=4 另一个一元一次方程是x+3=-4. 故答案为：D.4.解：此抛物线经过点A（-2，n），B（4，n）,抛物线的对称轴x=-2+42=1，又抛物线的对称轴直线x=-b2a=-b-2=b2,b2=1,b=2,函数解析式为：y=-x2+2x+4,将x=-2代入得y=-(-2)2+2（-2）+4=-4. 故答案为：A.5. 解：P点关于原点的对称点为P1(-3，- 83 ) 点P（3，83） P点关于x轴的对称点为P2(a，b) P2(3，-83) a=3，b=-83 原式=33-83=3-8=-2 故答案为：A 6.解：已知a=1，b=2，c=4，根据根与系数的关系可知：x1+x2
12、= ba =2，x1x2= ca =4， 故答案为：A.7.解：根据题意可知2014年的工资为2100（1+x）元，而2015年的工资为2100（1+x）（1+x）元，由此可列方程为 2100(1+x)2=2541 . 故答案为：C8.解：由题意得 x1 和 x2 为方程 kx+b=ax2 的两个根，即 ax2kxb=0 ， x1+x2=ka ， x1x2=ba ；1x1+1x2=x1+x2x1x2=kaba=kb ； 直线与 x 轴交点的横坐标为： x3=bk ，1x3=1x1+1x2 .x1x2=x2x3+x3x1 .故答案为： C .9.解：根据题意和图像可知：图中阴影部分的面积就是边长
13、为x的一个小正方形的面积，即y=x2,其图像应该是抛物线，从而排除了B,C，又00， m12 .故答案为： m1212.解：如图。当DEAB时，这时ABD=45，即 =45；如图，当DEBC时，EDB=CBD=45，ABD=ABC+CBD=30+45=75;即 =75；如图，当DEAC时，延长CB至DE于H，则BHE=ACB=90，HBE=90-BEH=45，CBE=180-HBE=180-45=135，ABE=ABC+CBE=30+135=165.即 =165；故答案为：45，75，165.13.解：抛物线与y轴的交点B（0,4），对称轴是直线x=2 CD=BD=2，AD=4 0yp4 S=
14、12CDyp=122yp=yp 0S4 14.解： ax2b (ab0) ， x=ba, 则 m1=-(2m4), 解得m=1, ba=m+1=2, ba=4. 故答案为：4.15.解：如图所示， 将BC绕着点C顺时针旋转90得FC,作直线FE交OM于H,则BCF=90，BC=FC，将CP绕点C按顺时针方向旋转90得CE，PCE=90，PC=EC，BCP=FCE，在BCP和FCE中，BC=FC，BCP=FCE，PC=EC，BCPFCE(SAS)，CBP=CFE，又BCF=90，BHF=90，点E在直线FH上，即点E的轨迹为直线FH，BHEF，当点E与点H重合时，BE=BH最短，当CPOM时，R
15、tBCP中，CBP=30，CP= 12 BC=2，BP= 3 CP=2 3 ，又PCE=CPH=PHE=90，CP=CE，正方形CPHE中，PH=CP=2，BH=BH+PH=2 3 +2，即BE的最小值为2 3 +2，故答案为：2 3 +2.16.解：把y=m+2代入y=-x2+2x+m+1中，得x2-2x+1=0， =4-4=0， 此方程两个相等的实数根， 则抛物线y=-x2+2x+m+1与直线y=m+2有且只有一个交点，故结论正确； 抛物线的对称轴为x=1， 点P（2，y3）关于x=1的对称点为P（0，y3）， a=-10， 当x1时，y随x增大而增大， 又-2012 ， 点M（-2，y1
16、）、 N(12,y2) 、点P（0，y3）在该函数图象上， y1y3y2 ， 故错误； 将该抛物线向左平移2个单位，再向下平移2个单位，抛物线的解析式为：y=-（x+2）2+2（x+2）+m+1-2，即y=-（x+1）2+m，故正确； 当m=1时，抛物线的解析式为：y=-x2+2x+2，A（0，2），C（2，2），B（1，3），作点B关于y轴的对称点B（-1，3），作C点关于x轴的对称点C（2，-2），连接BC，与x轴、y轴分别交于D、E点，如图， 则BE+ED+CD+BC=BE+ED+CD+BC=BC+BC，根据两点之间线段最短，知BC最短，而BC的长度一定，此时，四边形BCDE周长=BC+
17、BC最小，为：BM2+CM2+BM2+CM2=32+52+12+12=34+2,正确. 故答案为： 三、解答题（72分）17. 解：（）当m 12 时，方程为x2+x10，124（1）5，x 152 ，x1 1+52 ，x2 152 ；（）关于x的一元二次方程（2m+1）x2+4mx+2m30有两个不相等的实数根，0且2m+10，即（4m）24（2m+1）（2m3）0且m 12 ，m 34 且m 12 .18. （1）解：抛物线y=-x2+bx+c经过A(4，0)，B(0，2) 16+4b+c=0c=2 ，解得 b=72c=2 抛物线的解析式为y=-x2+ 72 x+2（2）解：C点是抛物线的
18、顶点， 由解析式可知C点坐标为( 74 ， 8116 )S四边形ADBC=SBDC+SADC= 1248116=818 19. （1）解:AM=AD+DM=40，或AM=AD-DM=20. 显然MAD不能为直角。当AMD为直角时AM2=AD2-DM2=302-102=800，AM=20 2 当ADM为直角时，AM2=AD2+CM2=302+102=1000 AM=10 10 （2）解:连结CD1由题意得D1AD2=90， AD1=AD2=30AD2D1=45，D1D2=30 2 又AD2C=135，CD2D1=90CD1= CD22+D1D22 =30 6 BAC=D2AD1=90OC)的长分
19、别是一元二次方程x2-14x+48=0的两个实数根，OC=6，C(0，6)（2）解：设直线MN的解析式是y=kx+b， 由(1)知OA=8，A(8，0)，点A，C都在直线MN上， 8k+b=0b=6 ,解得 k=34b=6 直线MN的解析式是y= 34 x+ 6（3）解：A(8，0)，C(0，6)根据题意，知B(8，6)， 点P在直线MN上，设P(a， 34 a+6)，当以点P，BC三点为顶点的三角形是等腰三角形时，需分类讨论： 当PC=PB时，点P是线段BC的中垂线与直线MN的交点，则P1(4，3)；当PC=BC时，a2+( 34 a+6-6)2=64，解得，a= 325 ，则P2(- 32
20、5 ， 545 )，P3( 325 ， 65 )；当PB=BC时，(a-8)2+(- 34 a+6-6)2=64，解得a= 25625 ，则- 34 a+6=- 4225 ，P4( 25625 ，- 4225 )，综上所述，符合条件的点P有：P1(4，3)，P2(- 325 ， 545 )，P3( 325 ， 65 )；P4( 25625 ，- 4225 )21. （1）90（2）解：当1090时，y=(2600-2400)x=200x，即 y=5x2+650x(1090,且x为整数) （3）解：因为要满足购买数量越多，所获利润越大，所以随x增大而增大 函数y=200x是y随x增大而增大，而函
21、数y=-5x2+650x=-5(x-65)2+21125，当10x65时，y随x增大而增大，当65x90时，y随x增大而减小，若一次购买65件时，设置为最低售价，则可避免y随x增大而减小的情况发生，故当x=65时，设置最低售价为3000-5(65-10)=2725(元)，答：公司应将最低销售单价调整为2725元22. （1）解：四边形ABCD是矩形 OABC8，OCAB10，OCB90将矩形OABC绕点O逆时针方向旋转（0180）得到矩形ODEFOFOC10，EFBC8，FOCB90OE OF2+EF2 100+64 2 41 点E（0， 241 ）（2）解：如图，连接BO交AC于点H， 四边
22、形ABCD是矩形ACOB，AHOHOAHAOH，且BAOCOA90ABOACO，将矩形OABC绕点O逆时针方向旋转（0180）得到矩形ODEFDEABOC，OEBO，ODOA，ABODEO，EDOBAO90，BOAEOD，ACODEO点C，点E，点O，点D四点共圆，CEDCOD，ECOEDO90，EDCEOD，ODOAOAHODAODAEODADOECDEOEDOCD，且DEOC，DECCODECDODC（AAS）ECDODCECODOABC8，ECO90ECO+BCO180点E，点C，点B共线ECBC，OCBC点B，点E关于OC对称，且B（8，10）点E（8，10）（3）解：如图，当点M在点
23、B右侧，连接ON，过点N作NGOD于G， BM 12 BN，设BMx，则BN2x，MN3x，NGOD，FEDEDO90四边形NEDG是矩形NGDE10ABCOSOMN 12 MNOC 12 OMNGOMMN3x，OC2+CM2OM2 ， 100+（x+8）29x2 ， x 2+862 （负值舍去）BN2+ 86 NCBNBC 86 6，点N（6 86 ，10）如图，若点M在点B左侧，连接ON，过点N作NGOD于G，BM 12 BN，设BMx，则BN2x，MNx，NGOD，FEDEDO90四边形NEDG是矩形NGDE10ABCOSOMN 12 MNOC 12 OMNGOMMNx，OC2+CM2O
24、M2 ， 100+（x8）2x2 ， x 414 BN2 414 412 NCBNBC 252 点N（ 252 ，10）综上所述：点N（6 86 ，10），（ 252 ，10）23. （1）解：将 A(1,0) 与 C(0,4) 分别代入二次函数y=-x2+bx+c得-12-b+c=0c=4 ， 解得b=3c=4;将点 A(1,0) 代入一次函数y=x+a得-1+a=0，解得 a=1， a=1,b=3,c=4 ； （2）解：由（1）所求的a,b,c的值可得一次函数的解析式为： y=x+1，抛物线的解析式为：y=x2+3x+4 ，联立 y=x+1与y=x2+3x+4 得y=x+1y=-x2+3x
25、+4,解得x=3y=4点D的坐标为：(3,4) ，设点E（ m ， m2+3m+4 ）， 过点E作x轴的垂线l,交x轴于点G,交AD于点H,则点H的坐标为(m,m+1).过点D作l的垂线，垂足为T；EH=-m2+2m+3,AD=4,SAED=SAEH+SHED= 12 EHAG+ 12 EHDT= 12 EH(AG+DT)=12 (m2+3m+4m1)4=2(m1)2+8，当m=1时,最大值为8,此时点E的坐标为(1,6)；（3）解：过A作y轴的平行线AS，过F作FGy轴交AS于点M，过F作FNx轴于N，点D的坐标为(3,4),点A坐标为(1,0)DAB=45AD平分SAB，FM=FNd=FE
26、+FM1=FE+FN1显然，当N、F.E所在直线与x轴垂直时，d=FE+FN1最小，最小值为61=5.此时点F的横坐标为1,代入y=x+1得F点的坐标为(1,2)24. （1）解：由题意可知： a+b+c=09a3b+c=0c=3 解得： a=1b=2c=3 抛物线的解析式为：y=x22x+3（2）解：PBC的周长为：PB+PC+BC BC是定值，当PB+PC最小时，PBC的周长最小，点A.点B关于对称轴I对称，连接AC交l于点P，即点P为所求的点 AP=BPPBC的周长最小是：PB+PC+BC=AC+BCA（3，0），B（1，0），C（0，3），AC=3 2 ，BC= 10 PBC的周长最小是： 32+10 （3）解：抛物线y=x22x+3顶点D的坐标为（1，4） A（3，0）直线AD的解析式为y=2x+6点E的横坐标为m，E（m，2m+6），F（m，m22m+3）EF=m22m+3（2m+6）=m24m3S=SDEF+SAEF=EFGH+EFAC=EFAH=（m24m3）2=m24m3；S=m24m3=（m+2）2+1；当m=2时，S最大，最大值为1此时点E的坐标为（2，2）
