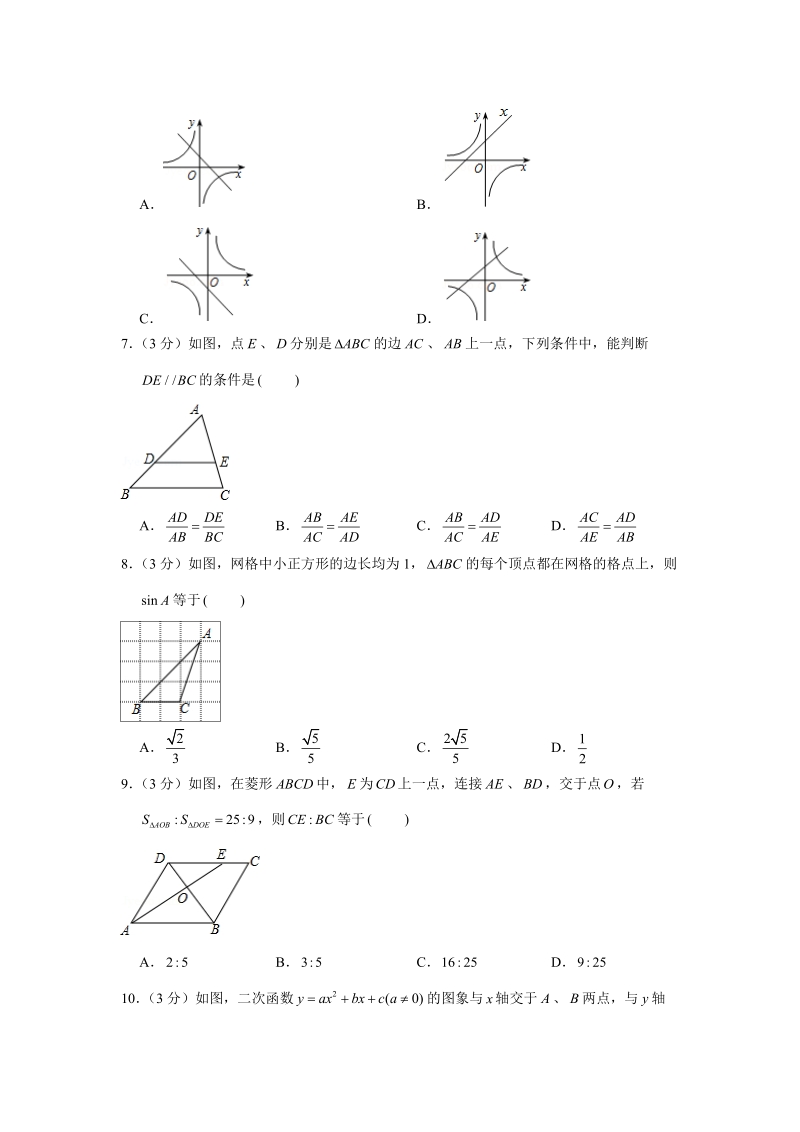
1、2019-2020学年山西省太原五中九年级（上）月考数学模拟试卷一、选择题1（3分）ABC1D2（3分）关于反比例函数，下列说法不正确的是A点在它的图象上B它的图象在第二、四象限C当时，D当时，随的增大而减小3（3分）将抛物线向左平移1个单位，再向下平移3个单位长度，所得的抛物线为ABCD4（3分）已知点将线段黄金分割，则下列各式中不正确的是ABCD5（3分）如图，几何体的左视图是ABCD6（3分）在同一直角坐标系中，函数和的大致图象是ABCD7（3分）如图，点、分别是的边、上一点，下列条件中，能判断的条件是ABCD8（3分）如图，网格中小正方形的边长均为1，的每个顶点都在网格的格点上，则等于
2、ABCD9（3分）如图，在菱形中，为上一点，连接、，交于点，若，则等于ABCD10（3分）如图，二次函数的图象与轴交于、两点，与轴交于点，且对称轴为直线，点的坐标为则下面的五个结论：；当时，或；，其中正确的个数是A2 个B3 个C4 个D5 个二、填空题11（3分）二次函数图象的顶点坐标是12（3分）如图， 一辆小车沿坡度为的斜坡向上行驶 13 米， 则小车上升的高度是米 13（3分）如图，是由一些相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体个数最多为个14（3分）如图， 已知点是反比例的图象上的一个动点， 连接，且，那么经过点的反比例函数图象的表达式为15（3分）如图，是的
3、中位线，是的中点，的延长线交于点，若的面积为，则的值为三、解答题16计算（1）（2）17（8分）在如图的方格中，的顶点坐标分别为、，与是关于点为位似中心的位似图形（1）在图中标出位似中心的位置，并写出点的坐标及与的相似比；（2）以原点为位似中心，在轴的左侧画出的一个位似，使它与的位似比为，并写出点的对应点的坐标18（7分）清明节假期，小红和小阳随爸妈去旅游，他们在景点看到一棵古松树，小红惊讶的说：“呀！这棵树真高！有60多米”小阳却不以为然：“60多米？我看没有”两个人争论不休，爸爸笑着说：“别争了，正好我带了一副三角板，用你们学过的知识量一量、算一算，看谁说的对吧！”小红和小阳进行了以下测量
4、：如图所示，小红和小阳分别在树的东西两侧同一地平线上，他们用手平托三角板，保持三角板的一条直角边与地平面平行，然后前后移动各自位置，使目光沿着三角板的斜边正好经过树的最高点，这时，测得小红和小阳之间的距离为135米，他们的眼睛到地面的距离都是1.6米通过计算说明小红和小阳谁的说法正确（计算结果精确到（参考数据，19如图，已知反比例函数的图象与一次函数的图象交于点和点，一次函数的图象交轴于点（1）求这两个函数的关系式；（2）求的面积；（3）结合图象直接写出时，的取值范围20（8分）某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取
5、适当的降价措施调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台（1）假设每台冰箱降价元，商场每天销售这种冰箱的利润是元，请写出与之间的函数表达式；（不要求写自变量的取值范围）（2）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？21（9分）如图，点、在一条直线上，与相交于点，连接（1）求证：；（2）若，求的度数：22如图，已知抛物线的顶点坐标为，且与轴交于点，与轴交于、两点（点在点的右侧），点是抛物线上的一动点，从点沿抛物线向点运动（点与不重合），过点作轴，交于点（1）求该抛物线的函数关系式及、两点的坐标；（2）求点在运动的过程中，线段的最大值；（3）若点与点
6、重合，点在轴上，点在抛物线上，问是否存在以，为顶点的平行四边形？若存在，直接写出点的坐标；若不存在，请说明理由参考答案与试题解析一、选择题1（3分）ABC1D【分析】根据特殊角的三角函数值求解即可【解答】解：故选：【点评】本题考查了特殊角的三角函数值，解答本题的关键在于熟练掌握各特殊角的三角函数值2（3分）关于反比例函数，下列说法不正确的是A点在它的图象上B它的图象在第二、四象限C当时，D当时，随的增大而减小【分析】利用反比例函数的性质可解【解答】解：当，双曲线的两支分别位于第二、第四象限，在每一象限内随的增大而增大反比例函数的图象分别位于第二、第四象限，在每一象限内随的增大而增大故选：【点评
7、】本题考查了反比例函数的性质，熟练掌握反比例函数的性质是本题的关键3（3分）将抛物线向左平移1个单位，再向下平移3个单位长度，所得的抛物线为ABCD【分析】按照“左加右减，上加下减”的规律【解答】解：将抛物线向左平移1个单位，再向下平移3个单位长度，得；故所得抛物线的解析式为故选：【点评】主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减并用规律求函数解析式4（3分）已知点将线段黄金分割，则下列各式中不正确的是ABCD【分析】根据黄金分割的定义：把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值叫做黄金比，据此判断即可【
8、解答】解：点将线段黄金分割，是较长的线段，根据黄金分割的定义可知：，故选：【点评】本题主要考查了黄金分割，应该识记黄金分割的公式：较短的线段原线段的倍，较长的线段原线段的倍，难度适中5（3分）如图，几何体的左视图是ABCD【分析】找到从几何体左面看得到的平面图形即可【解答】解：从几何体左面看得到是矩形的组合体，且长方形靠左故选：【点评】此题主要考查了三视图的相关知识；掌握左视图是从几何体左面看得到的平面图形是解决本题的关键6（3分）在同一直角坐标系中，函数和的大致图象是ABCD【分析】根据的取值范围，分别讨论和时的情况，然后根据一次函数和反比例函数图象的特点进行选择正确答案【解答】解：当时，一
9、次函数经过一、二、三象限，反比例函数的的图象经过一、三象限，故选项的图象符合要求；当时，一次函数经过二、三、四象限，反比例函数的的图象经过二、四象限，没有符合该条件的选项故选：【点评】此题考查反比例函数的图象问题；用到的知识点为：反比例函数与一次函数的值相同，则两个函数图象必有交点；一次函数与轴的交点与一次函数的常数项相关7（3分）如图，点、分别是的边、上一点，下列条件中，能判断的条件是ABCD【分析】根据平行线的判定定理判断即可；【解答】解：选项正确理由：，故选：【点评】本题考查平行线的判定，解题的关键是熟练掌握基本知识，属于中考常考题型8（3分）如图，网格中小正方形的边长均为1，的每个顶点
10、都在网格的格点上，则等于ABCD【分析】如图，作于在中，求出，即可解决问题；【解答】解：如图，作于，在中，故选：【点评】本题考查解直角三角形，勾股定理，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题9（3分）如图，在菱形中，为上一点，连接、，交于点，若，则等于ABCD【分析】由题意可得，则可证，可得，即可求【解答】解：四边形是菱形，设，则，故选：【点评】本题考查了相似三角形的判定和性质，菱形的性质，熟练运用相似三角形的性质是本题的关键10（3分）如图，二次函数的图象与轴交于、两点，与轴交于点，且对称轴为直线，点的坐标为则下面的五个结论：；当时，或；，其中正确的个数是
11、A2 个B3 个C4 个D5 个【分析】根据抛物线开口方向、对称轴、抛物线与轴的交点确定、的符号，根据函数图象确定和时，的取值范围【解答】解：对称轴为直线，故正确；抛物线开口方向向下，且对称轴在 轴右侧，图象与 轴交于正半轴，故错误；当 时，对应图象在 轴以下的部分，或故错误；当 时，又，故正确；当 时，函数有最大值， 故正确综上所述，正确的结论有3个故选：【点评】本题考查的是二次函数的图象与系数的关系，二次函数系数符号由抛物线开口方向、对称轴、抛物线与轴的交点抛物线与轴交点的个数确定二、填空题11（3分）二次函数图象的顶点坐标是【分析】利用配方法把二次函数解析式配成顶点式，然后利用二次函数的
12、性质求解【解答】解：，所以顶点坐标为【点评】本题考查二次函数的性质，解答本题的关键是将题目中的函数解析式化为顶点式12（3分）如图， 一辆小车沿坡度为的斜坡向上行驶 13 米， 则小车上升的高度是 5 米 【分析】由坡度定义可得位置升高的高度即为坡角所对的直角边 根据题意可得，米， 可解出直角边，即得到小车上升的高度 【解答】解： 由题意得，答： 小车上升的高度是 5 米 【点评】考查了解直角三角形的应用坡度坡角问题， 此题的关键是熟悉且会灵活应用公式：（坡 度）垂直高度水平宽度， 综合利用了勾股定理 13（3分）如图，是由一些相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体个数
13、最多为9个【分析】先由主视图和左视图得出前行左列一定是3个，剩下的三个位置最多每个位置有2个，然后相加即可【解答】解：由主视图和左视图知，前行左列一定是3个，而剩下的三个位置最多每个位置有2个，所以最多有9个故答案为：9【点评】此题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就容易得到答案了14（3分）如图， 已知点是反比例的图象上的一个动点， 连接，且，那么经过点的反比例函数图象的表达式为【分析】过点作轴， 垂足为；过点作轴， 垂足为，如图， 证明得到，设点的反比例函数图象的表达式为，利用的几何意义得到，
14、然后解绝对值方程得到满足条件的的值即可 【解答】解： 过点作轴， 垂足为；过点作轴， 垂足为，如图，设点的反比例函数图象的表达式为，而，点的反比例函数图象的表达式为故答案为【点评】本题考查了用待定系数法求反比例函数的解析式： 设出含有待定系数的反比例函数解析式为常数，；把已知条件 （自 变量与函数的对应值） 带入解析式， 得到待定系数的方程；解方程， 求出待定系数；写出解析式 也考查了相似三角形的判定与性质 15（3分）如图，是的中位线，是的中点，的延长线交于点，若的面积为，则的值为6【分析】首先证明与的边和边上的高的比为，根据，即可推出解决问题；【解答】解：是的中位线，是的中点，与的边和边上
15、的高的比为，故答案为6【点评】本题考查三角形的中位线定理，相似三角形的判定和性质，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型三、解答题16计算（1）（2）【分析】（1）直接利用特殊角的三角函数值以及负指数幂的性质化简得出答案；（2）直接利用二次根式的性质以及特殊角的三角函数值化简得出答案【解答】解：（1）原式；（2）原式【点评】此题主要考查了实数运算，正确化简各数是解题关键17（8分）在如图的方格中，的顶点坐标分别为、，与是关于点为位似中心的位似图形（1）在图中标出位似中心的位置，并写出点的坐标及与的相似比；（2）以原点为位似中心，在轴的左侧画出的一个位似，使它与的位似
16、比为，并写出点的对应点的坐标【分析】（1）连结且延长，连结且延长，它们的交点为点，由于，则与的相似比为；（2）延长到使，延长到使，连结，则可得到，然后写出的坐标【解答】解：（1）如图，点的坐标为，与的相似比为；（2）如图，为所求，的坐标为【点评】本题考查了作图位似变换：先确定位似中心，分别连接并延长位似中心和能代表原图的关键点，再根据位似比，确定能代表所作的位似图形的关键点，然后顺次连接上述各点，得到放大或缩小的图形18（7分）清明节假期，小红和小阳随爸妈去旅游，他们在景点看到一棵古松树，小红惊讶的说：“呀！这棵树真高！有60多米”小阳却不以为然：“60多米？我看没有”两个人争论不休，爸爸笑着
17、说：“别争了，正好我带了一副三角板，用你们学过的知识量一量、算一算，看谁说的对吧！”小红和小阳进行了以下测量：如图所示，小红和小阳分别在树的东西两侧同一地平线上，他们用手平托三角板，保持三角板的一条直角边与地平面平行，然后前后移动各自位置，使目光沿着三角板的斜边正好经过树的最高点，这时，测得小红和小阳之间的距离为135米，他们的眼睛到地面的距离都是1.6米通过计算说明小红和小阳谁的说法正确（计算结果精确到（参考数据，【分析】由题意得，四边形是矩形，于是得到米，米，设米，解直角三角形即可得到结论【解答】解：如图，表示古松树的高，分别表示小红和小阳的眼睛到地面的距离；由题意得，四边形是矩形，米，米
18、，设米，米，米，古松树高米米，小阳的说法正确【点评】考查了解直角三角形的问题该题是一个比较常规的解直角三角形问题，建立模型比较简单，但求解过程中涉及到根式和小数，算起来麻烦一些19如图，已知反比例函数的图象与一次函数的图象交于点和点，一次函数的图象交轴于点（1）求这两个函数的关系式；（2）求的面积；（3）结合图象直接写出时，的取值范围【分析】（1）把代入能求出反比例函数关系式，把点坐标代入反比例函数关系式求出的坐标，把、的坐标代入一次函数解析式，能求出一次函数解析式（2）把代入一次函数解析式求出，根据三角形面积公式求出的面积即可（3）根据图象时，即反比例函数在一次函数上方时对应的的值【解答】解
19、：（1）把代入得：，把代入解析式得：解得：，即，把、的坐标代入得：，解得：，一次函数的关系式是（2）把代入得：，解得：，即，过作轴于，过作轴于，的面积；（3）由图象得：当时，的取值范围是：或【点评】本题考查了一次函数与反比例函数的交点问题，用待定系数法求函数解析式，三角形面积的应用，主要考查学生的计算能力20（8分）某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台（1）假设每台冰箱降价元，商场每天销售这种冰箱的利润是元，请写出与之间的函数表达式；（不要求
20、写自变量的取值范围）（2）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？【分析】根据题意易求与之间的函数表达式（2）已知函数解析式，设可从实际得的值（3）利用求出的值，然后可求出的最大值【解答】解：（1）根据题意，得，即；（3）对于，当时，（元所以，每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元【点评】本题考查了二次函数的应用，求二次函数的最大（小值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法借助二次函数解决实际问题21（9分）如图，点、在一条直线上，与相交于点，连接（1）求证：；（2）若，求的度数：【分析】
21、（1）由，推出，可得，再根据两边成比例夹角相等两三角形相似即可证明；（2）利用相似三角形的性质即可解决问题；【解答】（1）证明：，即，（2）解：，【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型22如图，已知抛物线的顶点坐标为，且与轴交于点，与轴交于、两点（点在点的右侧），点是抛物线上的一动点，从点沿抛物线向点运动（点与不重合），过点作轴，交于点（1）求该抛物线的函数关系式及、两点的坐标；（2）求点在运动的过程中，线段的最大值；（3）若点与点重合，点在轴上，点在抛物线上，问是否存在以，为顶点的平行四边形？若存在，直接写出点的坐标；若不存在，请说明
22、理由【分析】（1）由抛物线的顶点坐标，可得出抛物线的顶点式，代入点的坐标可求出的值，进而可得出抛物线的函数关系式，再利用二次函数图象上点的坐标特征可求出点，的坐标；（2）由点，的坐标，利用待定系数法可求出直线的函数关系式，设点的坐标为，则点的坐标为，进而可得出，再利用二次函数的性质即可解决最值问题；（3）分为边及为对角线两种情况考虑：以为边构造平行四边形，平移直线交轴于点，交抛物线于点，由点的坐标可设点的坐标为，利用二次函数图象上点的坐标特征可求出的值，进而可得出点的坐标；以为对角线进行构造平行四边形，由点，的纵坐标为0，可得出点的纵坐标为，此时点，重合，进而可得出不存在这种情况，舍去综上，此
23、题得解【解答】解：（1）抛物线的顶点为，抛物线的函数关系式为，将代入，得：，解得：，抛物线的函数关系式为，即当时，有，即，解得：，又抛物线与轴交于，两点（点在点的右侧），点的坐标为，点的坐标为（2）设直线的函数关系式为，将，代入，得：，解得：，直线的函数关系式为设点的坐标为，则点的坐标为，当时，取得最大值，最大值为（3）分两种情况考虑：以为边构造平行四边形，平移直线交轴于点，交抛物线于点，点的坐标为，设点的坐标为，解得：，点的坐标为，和，；以为对角线进行构造平行四边形，点，的纵坐标为0，点的纵坐标为，此时点，重合，不存在这种情况，舍去综上所述，符合条件的点有两个，即，和，【点评】本题考查了二次函数的三种形式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、待定系数法求一次函数解析式、二次函数的性质以及平行四边形的性质，解题的关键是：（1）根据点的坐标，利用待定系数法求出抛物线的函数关系式；（2）由点，的坐标，找出；（3）分为边及为对角线两种情况找出点的坐标
