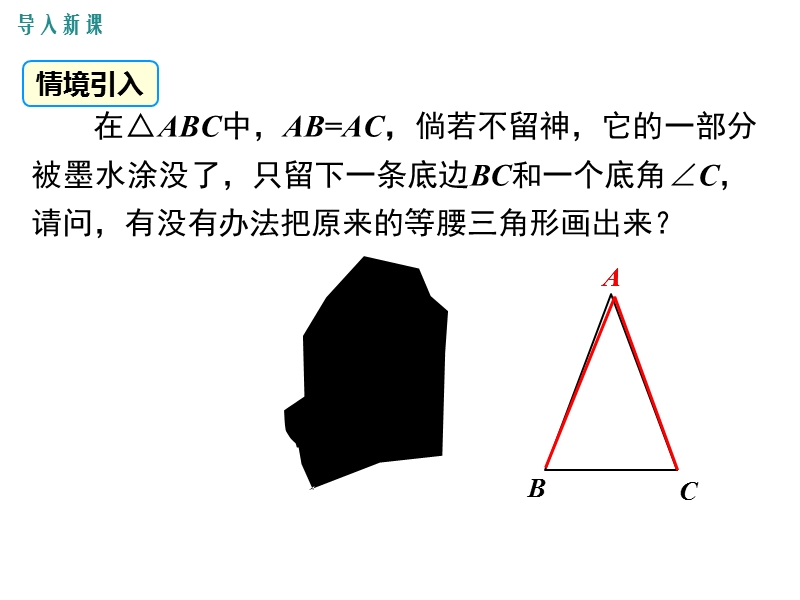
1、13.3 等腰三角形,第十三章 轴对称,导入新课,讲授新课,当堂练习,课堂小结,第2课时 等腰三角形的判定,八年级数学上（RJ）,1 .掌握等腰三角形的判定方法.（重点） 2.掌握等腰三角形的判定定理，并运用其进行证明和计算.（难点）,导入新课,情境引入,在ABC中，AB=AC，倘若不留神，它的一部分被墨水涂没了，只留下一条底边BC和一个底角C，请问，有没有办法把原来的等腰三角形画出来？,A,B,C,A,思考：如图，在ABC中，如果B=C，那么AB与AC之间有什么关系吗？,我测量后发现AB与AC相等.,3cm,3cm,讲授新课,A,B,C,如图，位于海上B、C两处的两艘救生船接到A处遇险船只的
2、报警，当时测得B=C.如果这两艘救生船以同样的速度同时出发，能不能同时赶到出事地点（不考虑风浪因素）？,互动探究,已知：如图，在ABC中, B=C,那么它们所对的边AB和AC有什么数量关系?,建立数学模型：,做一做：画一个ABC，其中B=C=30，请你量一量AB与AC的长度，它们之间有什么数量关系，你能得出什么结论？,AB=AC,你能验证你的结论吗？,在ABD与ACD，,1=2，, ABD ACD.,B=C，,AD=AD，,AB=AC.,过A作AD平分BAC交BC于点D.,证明：, AC=AB. ( ) 即ABC为等腰三角形.,B=C， ( ),知识要点,等腰三角形的判定方法,如果一个三角形有
3、两个角相等,那么这个三角形是等腰三角形（简写成“等角对等边”）.,已知,等角对等边,在ABC中，,应用格式：,(,(,（等角对等边）.,（等角对等边）.,错，因为都不是在同一个三角形中.,辨一辨：如图,下列推理正确吗?,例1 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形,已知： 如图，CAE是ABC的外角，1=2，ADBC,求证：AB=AC,证明：ADBC， 1=B（两直线平行，同位角相等），2=C（两直线平行，内错角相等）又1=2，B=C，AB=AC（等角对等边）,例2 已知：如图，AB=DC,BD=CA,BD与CA相交于点E. 求证：AED是等腰三角形.,
4、证明：AB=DC,BD=CA,AD=DA,ABDDCA(SSS),ADB=DAC(全等三角形的对应角相等）,AE=DE(等角对等边）, AED是等腰三角形.,例3 已知：如图，ADBC，BD平分ABC. 求证：AB=AD,证明： ADBC，ADB=DBC. BD平分ABC，ABD=DBC，ABD=ADB，AB=AD.,总结：平分角+平行=等腰三角形,如图，把一张长方形的纸沿着对角线折叠， 重合部分是一个等腰三角形吗？为什么？,B,C,A,D,E,变式训练,是,由折叠可知，EBD=CBD.,ADBC，EDB=CBD，,EDB=EBD， BE=DE，EBD是等腰三角形.,练一练： 1.在ABC中，
5、A和B的度数如下，能判定 ABC是等腰三角形的是（ ） A. A50，B70 B. A70，B40 C. A30，B90 D. A80，B60,B,2.如图，已知OC平分AOB，CDOB，若OD3cm，则CD等于_.,3cm,例4 已知等腰三角形底边长为a,底边上的高的长为h，求作这个等腰三角形.,a,h,作法：1.作线段AB=a. 2.作线段AB的垂直平分线MN，交AB 于点D. 3.在MN上取一点C，使DC=h. 4.连接AC，BC，则ABC即为所求.,C,D,例5 如图，在ABC中，ACB90，CD是AB边上的高，AE是BAC的平分线，AE与CD交于点F，求证：CEF是等腰三角形,证明：
6、在ABC中，ACB90， BBAC90. CD是AB边上的高，ACDBAC90， BACD. AE是BAC的平分线，BAEEAC， BBAEACDEAC，即CEFCFE， CECF，CEF是等腰三角形,方法总结：“等角对等边”是判定等腰三角形的重要依据，是先有角相等再有边相等，只限于在同一个三角形中，若在两个不同的三角形中，此结论不一定成立,例6 如图，在ABC中，AB=AC，ABC和ACB的平分线交于点O.过O作EFBC交AB于E，交AC于F. 探究EF、BE、FC之间的关系.,解：EF=BE+CF. 理由如下： EFBC, EOB=CBO，FOC=BCO. BO、CO分别平分ABC、ACB
7、，CBOABO，BCOACO， EOBABO ，FOCACO， BEOE，CF=OF， EF=EO+FOBE+CF.,方法总结：判定线段之间的数量关系，一般做法是通过全等或利用“等角对等边”，运用转化思想，解决问题.,当堂练习,1.如图，在ABC中，ABAC，A36，BD、CE分别是ABC、BCD的角平分线，则图中的等腰三角形有( ) A5个 B4个 C3个 D2个,2.一个三角形的一个外角为130，且它恰好等于一个不相邻的内角的2倍.这个三角形是（ ） A钝角三角形 B直角三角形 C等腰三角形 D等边三角形,C,A,3.如图，直线a、b相交于点O，1=50，点A在直线a上，直线b上存在点B，
8、使以点O、A、B为顶点的三角形是等腰三角形，这样的B点有（ ） A1个 B2个 C3个 D4个,O,a,b,D,A,4.如图，已知A=36，DBC=36，C=72，则DBC=_，BDC=_，图中的等腰三角形有_.,36,72,ABC、,DBA、,BCD,5.如图，在ABC中，ABC和ACB的平分线交于点E，过点E作MNBC交AB于M，交AC于N，若BMCN9，则线段MN的长为_.,9,第4题图,第5题图,6.如图,上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得NAC=40，NBC=80.求从B处到灯塔C的距离.,解：NBC=A+C，
9、C=80- 40= 40， C = A， BA=BC（等角对等边）. AB=20（12-10）=40(海里), BC=40海里. 答：B处距离灯塔C40海里.,7.已知：如图，四边形ABCD中，ABAD，BD.求证：BCCD.,证明：连接BD. AB=AD， ABD=ADB. ABC=ADC， ABC-ABD=ADC-ADB， 即DBC=BDC， BC=CD.,8.在ABC中，AB=AC，倘若不留神，它的一部分被墨水涂没了，只留下一条底边BC和一个底角C，请问，有没有办法把原来的等腰三角形画出来？,A,B,C,3种“补出”方法：方法1：量出C度数，画出BC， B与C的边相交得到顶点A方法2：作BC边上的垂直平分线，与C的一边相交得到顶点A方法3：对折,课堂小结,等腰三角形的判定,等角对等边,定义,注意是指同一个三角形中,有两边相等的三角形是等腰三角形,
