1、2017-2018学年河南省洛阳市七年级（下）期末数学试卷一、选择题（每小题3分，共30分）1（3分）计算的平方根为（）A4B2C4D2（3分）如图，直线a、b被直线c所截，155，下列条件中能判定ab的是（）A235B245C255D2653（3分）已知关于x，y的二元一次方程组的解为，则a2b的值是（）A2B2C3D34（3分）不等式64x3x8的非负整数解为（）A2个B3个C4个D5个5（3分）如图表示下列四个不等式组中其中一个的解集，这个不等式组是（）ABCD6（3分）正整数x、y满足（2x5）（2y5）25，则x+y等于（）A18或10B18C10D267（3分）如图所示，点E在AC
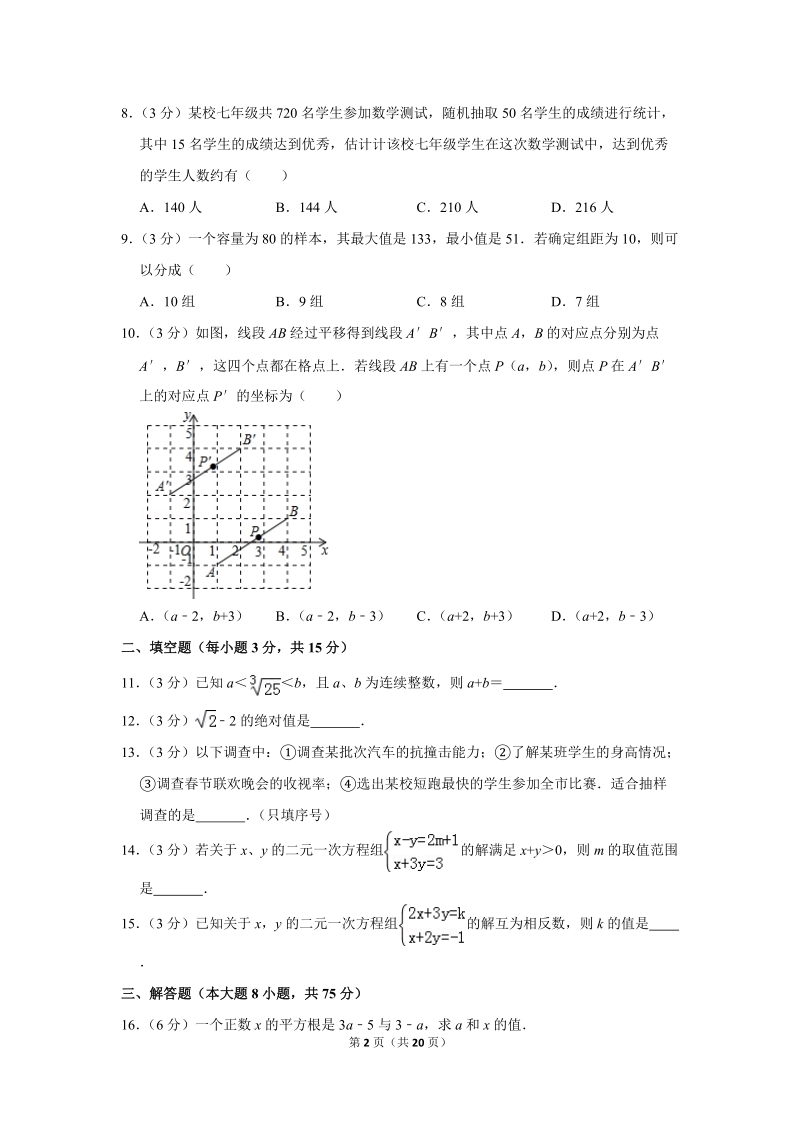
2、的延长线上，下列条件中能判断ABCD（）A12B34CDDCEDD+ACD1808（3分）某校七年级共720名学生参加数学测试，随机抽取50名学生的成绩进行统计，其中15名学生的成绩达到优秀，估计计该校七年级学生在这次数学测试中，达到优秀的学生人数约有（）A140人B144人C210人D216人9（3分）一个容量为80的样本，其最大值是133，最小值是51若确定组距为10，则可以分成（）A10组B9组C8组D7组10（3分）如图，线段AB经过平移得到线段AB，其中点A，B的对应点分别为点A，B，这四个点都在格点上若线段AB上有一个点P（a，b），则点P在AB上的对应点P的坐标为（）A（a2，b
3、+3）B（a2，b3）C（a+2，b+3）D（a+2，b3）二、填空题（每小题3分，共15分）11（3分）已知ab，且a、b为连续整数，则a+b 12（3分）2的绝对值是 13（3分）以下调查中：调查某批次汽车的抗撞击能力；了解某班学生的身高情况；调查春节联欢晚会的收视率；选出某校短跑最快的学生参加全市比赛适合抽样调查的是 （只填序号）14（3分）若关于x、y的二元一次方程组的解满足x+y0，则m的取值范围是 15（3分）已知关于x，y的二元一次方程组的解互为相反数，则k的值是 三、解答题（本大题8小题，共75分）16（6分）一个正数x的平方根是3a5与3a，求a和x的值17（12分）（1）解
4、方程组：（2）解不等式组：18（8分）如图，已知1+2180，3B，465，求证ACB4请填空完成证明过程：1+2180 ，1+ 1802DFE ABEF 3ADE 又3BADE DEBC ACB4 ACB6519（9分）四边形ABCD各顶点的坐标分别为A（0，1）、B（5，1）、C（7，3）、D（2，5）（1）在如图所示的平面直角坐标系画出该四边形；（2）四边形ABCD的面积是 ；（3）四边形ABCD内（边界点除外）一共有 个整点（即横坐标和纵坐标都是整数的点）20（9分）为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生
5、都自主选择一个类别的拓展性课程为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：根据统计图中的信息，解答下列问题：（1）求本次被调查的学生人数（2）将条形统计图补充完整（3）若该校共有1600名学生，请估计全校选择体育类的学生人数21（10分）如图，已知直线l1l2，直线l3和直线l1，l2交于点C和D，直线l3上有一点P（1）如图1，若P点在C，D之间运动时，问PAC，APB，PBD之间的关系是否发生变化，并说明理由；（2）若点P在C，D两点的外侧运动时（P点与点C，D不重合，如图2和3），试写出PAC，APB，PBD之间的关系，并
6、说明理由（图3只写结论，不写理由）22（10分）甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过200元后，超出200元的部分按90%收费；在乙商场累计购物超过100元后，超出100元的部分按95%收费，顾客到哪家商场购物花费少？23（11分）某中学为打造书香校园，计划购进甲、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元（1）甲、乙两种书柜每个的价格分别是多少元？（2）若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，
7、学校至多能够提供资金4320元，请设计几种购买方案供这个学校选择2017-2018学年河南省洛阳市七年级（下）期末数学试卷参考答案与试题解析一、选择题（每小题3分，共30分）1（3分）计算的平方根为（）A4B2C4D【分析】首先根据算术平方根的定义求出的值，然后根据平方根的定义即可求出结果【解答】解：4，又（2）24，4的平方根是2，即的平方根2故选：B【点评】本题主要考查了平方根的定义注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根2（3分）如图，直线a、b被直线c所截，155，下列条件中能判定ab的是（）A235B245C255D265【分析】同位角相等，两直线平行
8、，根据平行线的判定定理进行解答【解答】解：如图，若255，则355，13，ab，故选：C【点评】本题考查了平行线的判定正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行3（3分）已知关于x，y的二元一次方程组的解为，则a2b的值是（）A2B2C3D3【分析】把代入方程组，得出关于a、b的方程组，求出方程组的解即可【解答】解：把代入方程组得：，解得：，所以a2b2（）2，故选：B【点评】本题考查了解二元一次方程组和二元一次方程组的解，能得出关于a、b的方程组是解此题的关键4（3分）不等式64x3x8的非负整数解为（）
9、A2个B3个C4个D5个【分析】首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的非负整数即可【解答】解：移项得，4x3x86，合并同类项得，7x14，系数化为1得，x2故其非负整数解为：0，1，2，共3个故选：B【点评】本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键解不等式应根据不等式的基本性质5（3分）如图表示下列四个不等式组中其中一个的解集，这个不等式组是（）ABCD【分析】根据在数轴上表示不等式解集的方法即可得出答案【解答】解：3处是空心圆点，且折线向右，2处是实心圆点，且折线向左，这个不等式组的解集是3x2故选：D【点评】本题考查的是在数轴上
10、表示不等式的解集，熟知“小于向左，大于向右”是解答此题的关键6（3分）正整数x、y满足（2x5）（2y5）25，则x+y等于（）A18或10B18C10D26【分析】易得（2x5）、（2y5）均为整数，分类讨论即可求得x、y的值即可解题【解答】解：x、y是正整数，且最小的正整数为1，2x5是整数且最小整数为3，2y5是整数且最小的整数为325125，或2555，存在两种情况：2x51，2y525，解得：x3，y15，；2x52y55，解得：xy5；x+y18或10，故选：A【点评】本题考查了整数的乘法，本题中根据25125或2555分类讨论是解题的关键7（3分）如图所示，点E在AC的延长线上，
11、下列条件中能判断ABCD（）A12B34CDDCEDD+ACD180【分析】根据平行线的判定分别进行分析可得答案【解答】解：A、根据内错角相等，两直线平行可得ABCD，故此选项正确；B、根据内错角相等，两直线平行可得BDAC，故此选项错误；C、根据内错角相等，两直线平行可得BDAC，故此选项错误；D、根据同旁内角互补，两直线平行可得BDAC，故此选项错误；故选：A【点评】此题主要考查了平行线的判定，解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角8（3分）某校七年级共720名学生参加数学测试，随机抽取50名学生的成绩进行统计，其中15名学生的成绩达到优秀，估计计该校七年级学生
12、在这次数学测试中，达到优秀的学生人数约有（）A140人B144人C210人D216人【分析】根据题意可以求得达到优秀的学生人数，从而可以解答本题【解答】解：720216，即达到优秀的学生人数约有216人，故选：D【点评】本题考查用样本估计总体，解答本题的关键是明确题意，用样本估计出总体优秀的人数9（3分）一个容量为80的样本，其最大值是133，最小值是51若确定组距为10，则可以分成（）A10组B9组C8组D7组【分析】先根据最大值为133，最小值为51，求出最大值与最小值的差，再根据组数（最大值最小值）组距，即可求出答案【解答】解：最大值为133，最小值为51，最大值与最小值的差是13351
13、82，组距为10，8.2，可以分成9组故选：B【点评】本题考查了组数的计算，关键是掌握组数（最大值最小值）组距，注意小数部分要进位，不要舍去10（3分）如图，线段AB经过平移得到线段AB，其中点A，B的对应点分别为点A，B，这四个点都在格点上若线段AB上有一个点P（a，b），则点P在AB上的对应点P的坐标为（）A（a2，b+3）B（a2，b3）C（a+2，b+3）D（a+2，b3）【分析】根据点A、B平移后横纵坐标的变化可得线段AB向左平移2个单位，向上平移了3个单位，然后再确定a、b的值，进而可得答案【解答】解：由题意可得线段AB向左平移2个单位，向上平移了3个单位，则P（a2，b+3）故选
14、：A【点评】此题主要考查了坐标与图形的变化平移，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减二、填空题（每小题3分，共15分）11（3分）已知ab，且a、b为连续整数，则a+b5【分析】找到25位于2的立方和3的立方之间，则问题可解【解答】解：由于82527即23253323a2，b3a+b5故答案为：5【点评】本题考查了立方根的意义，解答时分别找到被开方数在哪两个立方数之间即可12（3分）2的绝对值是2【分析】根据负数的绝对值等于它的相反数解答【解答】解：2的绝对值是2即|2|2故答案为：2【点评】本题考查了实数的性质，主要利用了绝对值的性质13（3分）以下调查中：调查某批次汽车
15、的抗撞击能力；了解某班学生的身高情况；调查春节联欢晚会的收视率；选出某校短跑最快的学生参加全市比赛适合抽样调查的是（只填序号）【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，具体问题具体分析，普查结果准确，所以在要求精确、难度相对不大，实验无破坏性的情况下应选择普查方式，当考查的对象很多或考查会给被调查对象带来损伤破坏，以及考查经费和时间都非常有限时，普查就受到限制，这时就应选择抽样调查【解答】解：调查某批次的汽车的抗撞击力，危险性较大，而且破坏性较强，故应抽样调查；了解某班学生的身高情况，涉及人数较少，适合全面调查；调查春节联欢晚会的收视率，涉及人数较多，适合抽样调查；选
16、出某校跑得最快的学生参加全市比赛，涉及人数较少，适合全面调查故答案为：【点评】此题考查了抽样调查和全面调查，由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似14（3分）若关于x、y的二元一次方程组的解满足x+y0，则m的取值范围是m2【分析】首先解关于x和y的方程组，利用m表示出x+y，代入x+y0即可得到关于m的不等式，求得m的范围【解答】解：，+得2x+2y2m+4，则x+ym+2，根据题意得m+20，解得m2故答案是：m2【点评】本题考查的是解二元一次方程组和解一元一次不等式，解答此题的关键是把m当作已知数表示出x+y的值，再得到关于m的不等式1
17、5（3分）已知关于x，y的二元一次方程组的解互为相反数，则k的值是1【分析】将方程组用k表示出x，y，根据方程组的解互为相反数，得到关于k的方程，即可求出k的值【解答】解：解方程组得：，因为关于x，y的二元一次方程组的解互为相反数，可得：2k+32k0，解得：k1故答案为：1【点评】此题考查方程组的解，关键是用k表示出x，y的值三、解答题（本大题8小题，共75分）16（6分）一个正数x的平方根是3a5与3a，求a和x的值【分析】根据正数平方根的意义，先得到a的值，再计算x的值【解答】解：因为一个正数有两个平方根，它们互为相反数，所以正数x的平方根互为相反数，即3a5+3a0a1当a1时，3a5
18、2，x（2）24答：a和x的值分别是1和4【点评】本题考查了平方根的意义一个正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根17（12分）（1）解方程组：（2）解不等式组：【分析】（1）利用加减消元法求解可得；（2）分别求出各不等式的解集，再求出其公共解集【解答】解：（1），3，得：x4，将x4代入，得：4+y5，解得：y1，则方程组的解为；（2）解不等式2x9x，得：x3，解不等式5x13（x+1），得：x2，则不等式组的解集为x2【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键18（8分）如图，已知1+
19、2180，3B，465，求证ACB4请填空完成证明过程：1+2180已知，1+DFE1802DFE同角的补角相等ABEF内错角相等，两直线平行3ADE两直线平行，内错角相等又3BADEBDEBC同位角相等，两直线平行ACB4两直线平行，同位角相等ACB65【分析】根据平行线的判定和性质定理证明即可【解答】证明：1+2180 （已知），1+DFE1802DFE （同角的补角相等）ABEF （内错角相等，两直线平行）3ADE （两直线平行，内错角相等）又3BADEBDEBC （同位角相等，两直线平行）ACB4 （两直线平行，同位角相等）ACB65，故答案为：已知；DFE；同角的补角相等；内错角相等
20、，两直线平行；两直线平行，内错角相等；B；同位角相等，两直线平行；两直线平行，同位角相等【点评】本题考查的是平行线的判定和性质，掌握平行线的判定定理和性质定理是解题的关键19（9分）四边形ABCD各顶点的坐标分别为A（0，1）、B（5，1）、C（7，3）、D（2，5）（1）在如图所示的平面直角坐标系画出该四边形；（2）四边形ABCD的面积是17；（3）四边形ABCD内（边界点除外）一共有13个整点（即横坐标和纵坐标都是整数的点）【分析】（1）根据点的坐标描出四个点，顺次连接可得；（2）割补法求解即可；（3）根据整点的概念可得【解答】解：（1）如图所示，四边形ABCD即为所求；（2）四边形ABC
21、D的面积为：S四边形ABCD4722252417，即：四边形ABCD的面积为17，故答案为17；（3）由图可知，四边形ABCD内（边界点除外）的整点有13个，故答案为：13【点评】本题主要考查坐标与图形的性质，解题的关键是理解有序实数对与平面内的点一一对应及割补法求面积20（9分）为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：根据统计图中的信息，解答下列问题：（1）求本次被调查的学生
22、人数（2）将条形统计图补充完整（3）若该校共有1600名学生，请估计全校选择体育类的学生人数【分析】（1）根据条形统计图和扇形统计图可知选择劳技的学生60人，占总体的30%，从而可以求得调查学生人数；（2）根据文学的百分比和（1）中求得的学生调查数可以求得文学的有多少人，从而可以求得体育的多少人，进而可以将条形统计图补充完整；（3）根据调查的选择体育的学生所占的百分比可以估算出全校选择体育类的学生人数【解答】解：（1）6030%200（人），即本次被调查的学生有200人；（2）选择文学的学生有：20015%30（人），选择体育的学生有：2002460301670（人），补全的条形统计图如下图所
23、示，（3）1600（人）即全校选择体育类的学生有560人【点评】本题考查条形统计图、用样本估计总体、扇形统计图，解题的关键是明确题意，找出所求问题需要的条件、利用数形结合的思想解答问题21（10分）如图，已知直线l1l2，直线l3和直线l1，l2交于点C和D，直线l3上有一点P（1）如图1，若P点在C，D之间运动时，问PAC，APB，PBD之间的关系是否发生变化，并说明理由；（2）若点P在C，D两点的外侧运动时（P点与点C，D不重合，如图2和3），试写出PAC，APB，PBD之间的关系，并说明理由（图3只写结论，不写理由）【分析】（1）当P点在C、D之间运动时，首先过点P作PEl1，由l1l2
24、，可得PEl2l1，根据两直线平行，内错角相等，即可求得：APBPAC+PBD（2）当点P在C、D两点的外侧运动时，由直线l1l2，根据两直线平行，同位角相等与三角形外角的性质，即可求得：PBDPAC+APB【解答】解：（1）如图，当P点在C、D之间运动时，APBPAC+PBD理由如下：过点P作PEl1，l1l2，PEl2l1，PAC1，PBD2，APB1+2PAC+PBD；（2）如图2，当点P在C、D两点的外侧运动，且在l2下方时，PACPBD+APB理由如下：l1l2，PEDPAC，PEDPBD+APB，PACPBD+APB如图3，当点P在C、D两点的外侧运动，且在l1上方时，PBDPAC
25、+APB理由如下：l1l2，PECPBD，PECPAC+APB，PBDPAC+APB【点评】本题主要考查平行线的性质与三角形外角的性质此题难度适中，解题的关键是掌握：两直线平行，内错角相等与两直线平行，同位角相等，注意辅助线的作法22（10分）甲、乙两商场以同样的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过200元后，超出200元的部分按90%收费；在乙商场累计购物超过100元后，超出100元的部分按95%收费，顾客到哪家商场购物花费少？【分析】先设顾客累计花费x元，根据三种情况进行讨论，当x100时，若100x200，若x200，分别进行分析，即可得出答案【解答】解
26、：设顾客累计花费x元，根据题意得：（1）当x100时，两家商场都不优惠，则花费一样；（2）若100x200，去乙商场享受优惠，花费少；（3）若x200，在甲商场花费200+（x200）90%0.9x+20（元），在乙商场花费100+（x100）95%0.95x+5（元），到甲商场花费少，则0.9x+200.95x+5，解得x300；到乙商场花费少，则0.9x+200.95x+5，x300；到两家商场花费一样多，则0.9x+200.95x+5，x300【点评】此题考查了一元一次不等式的应用，关键是读懂题意，列出不等式，再根据实际情况进行讨论，不要漏项23（11分）某中学为打造书香校园，计划购进甲
27、、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元（1）甲、乙两种书柜每个的价格分别是多少元？（2）若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多能够提供资金4320元，请设计几种购买方案供这个学校选择【分析】（1）设甲种书柜单价为x元，乙种书柜的单价为y元，根据：若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元列出方程组求解即可；（2）设甲种书柜购买m个，则乙种书柜购买（20m）个根据：购买的
28、乙种书柜的数量甲种书柜数量且所需资金4320列出不等式组，解不等式组即可得不等式组的解集，从而确定方案【解答】（1）解：设甲种书柜单价为x元，乙种书柜的单价为y元，由题意得：， 解之得：，答：甲种书柜单价为180元，乙种书柜的单价为240元（2）解：设甲种书柜购买m个，则乙种书柜购买（20m）个；由题意得： 解之得：8m10因为m取整数，所以m可以取的值为：8，9，10即：学校的购买方案有以下三种：方案一：甲种书柜8个，乙种书柜12个，方案二：甲种书柜9个，乙种书柜11个，方案三：甲种书柜10个，乙种书柜10个【点评】本题主要考查二元一次方程组、不等式组的综合应用能力，根据题意准确抓住相等关系或不等关系是解题的根本和关键
