1、2017-2018学年广东省广州市天河区高一（上）期末数学试卷一、选择题（共12小题，每小题5分，满分60分）1（5分）直线x+y0的倾斜角为（）A45B60C120D1352（5分）已知集合A1，2，3，4，5，6，By|y，xA，则 AB（）A1，2B1，2，3C1，3，5D1，2，3，4，5，63（5分）函数f（x）lgx+x3的零点所在的区间是（）A（0，1）B（1，2）C（2，3）D（3，4）4（5分）如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是（）ABCD5（5分）已知a0.80.7，blog20.7，c1.30.8，则a，b
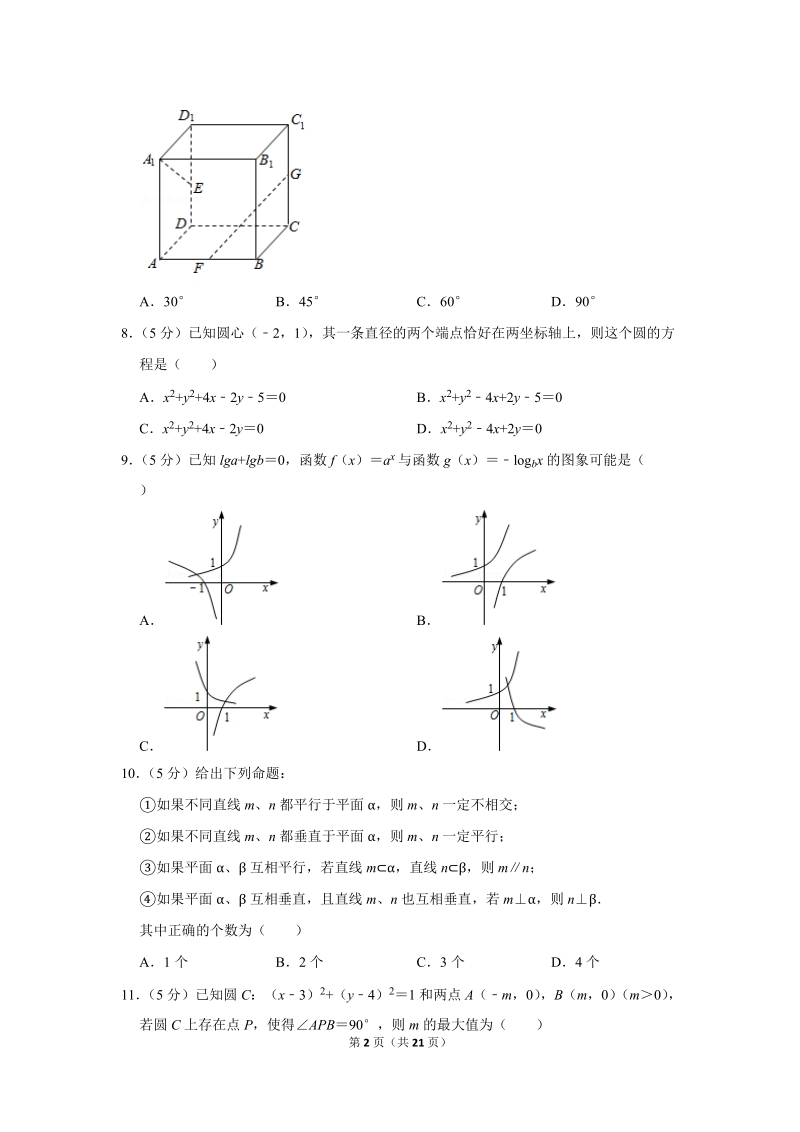
2、，c的大小关系是（）AabcBbacCcbaDcab6（5分）已知直线l1：x+2my10与直线l2：（m2）xmy+20平行，则实数m的值是（）AB或0CD或07（5分）如图，长方体ABCDA1B1C1D1中，AA1AB2，AD1，E，F，G分别是DD1，AB，CC1的中点，则异面直线A1E与GF所成角为（）A30B45C60D908（5分）已知圆心（2，1），其一条直径的两个端点恰好在两坐标轴上，则这个圆的方程是（）Ax2+y2+4x2y50Bx2+y24x+2y50Cx2+y2+4x2y0Dx2+y24x+2y09（5分）已知lga+lgb0，函数f（x）ax与函数g（x）logbx的图
3、象可能是（）ABCD10（5分）给出下列命题：如果不同直线m、n都平行于平面，则m、n一定不相交；如果不同直线m、n都垂直于平面，则m、n一定平行；如果平面、互相平行，若直线m，直线n，则mn；如果平面、互相垂直，且直线m、n也互相垂直，若m，则n其中正确的个数为（）A1个B2个C3个D4个11（5分）已知圆C：（x3）2+（y4）21和两点A（m，0），B（m，0）（m0），若圆C上存在点P，使得APB90，则m的最大值为（）A7B6C5D412（5分）偶函数f（x）（xR）满足：f（5）f（2）0，且在区间0，4与4，+）上分别递增和递减，则不等式xf（x）0的解集为（）A（，5）（2，2
4、）（5，+）B（5，2）（2，5）C（0，2）（5，+）D（5，2）（0，2）（5，+）二、填空题（共4小题，每小题5分，满分20分）13（5分）函数f（x）+log2（x+1）的定义域为 14（5分）已知一个四棱柱，其底面是正方形，侧棱垂直于底面，它的各个顶点都在一个表面积为4cm2的球面上如果该四棱柱的底面边长为1cm，则其侧棱长为 cm15（5分）已知mR，过原点O作圆x2+（m+2）y24x8y16m0的切线，则此时的切线方程为 16（5分）已知函数知f（x）满足对任意x1x2，都有f（x1）f（x2）成立，那么实数a的取值范围是
5、 三、解答题（共6小题，满分70分）17（10分）已知直线l1：（m2）x+my80和直线l2：mx+y30，其中m为常数（）若l1l2，求m的值；（）若点P（1，2m）在l2上，直线l过P点，且在两坐标轴上的截距之和为0，求直线l的方程18（12分）如图，三棱柱ABCA1B1C1内接于一个圆柱，且底面是正三角形，如果圆柱的体积是2，底面直径与母线长相等（）求该圆柱的侧面积；（）求三棱柱ABCA1B1C1的体积19（12分）已知函数f（x）ax+c是R上的奇函数（a，b，c是常数），且满足f（1）3，f（2）（）求a，b，c的值；（）试判断函数f（x）在区间（0，）上的单调性，并用定义证明20
6、（12分）如图，在四棱锥PABCD中，ABCD，ABAD，CD2AB，平面PAD底面ABCD，PAADE和F分别是CD和PC的中点，求证：（）BE平面PAD；（）PABC；（）平面BEF平面PCD21（12分）已知圆C的圆心为点C（0，3），点D（，2）在圆C上，直线l过点A（1，0）且与圆C相交P，Q两点，点M是线段PQ的中点（1）求圆C的方程：（2）若|AM|3，求直线l的方程22（12分）已知函数ylog2（4x+1）kx是偶函数，g（x）log2（a2xa）（其中a0）（）求g（x）的定义域；（）求k的值；（）若函数f（x）与g（x）的图象有且只有一个交点，求a的取值范围2017-20
7、18学年广东省广州市天河区高一（上）期末数学试卷参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1（5分）直线x+y0的倾斜角为（）A45B60C120D135【分析】由直线方程求出直线的斜率，再由倾斜角的正切值等于斜率求得直线的倾斜角【解答】解：由直线x+y0，可得直线的斜率为k1，设其倾斜角为，（0180），则tan1，135即直线x+y0的倾斜角的大小为135故选：D【点评】本题考查直线倾斜角的求法，考查倾斜角与斜率的关系，是基础题2（5分）已知集合A1，2，3，4，5，6，By|y，xA，则 AB（）A1，2B1，2，3C1，3，5D1，2，3，4，5，6【分析】由题
8、意求出集合B，由交集的运算求出AB【解答】解：因为A1，2，3，4，5，6，所以By|y，xA1，2，则AB1，2，故选：A【点评】本题考查交集及其运算，属于基础题3（5分）函数f（x）lgx+x3的零点所在的区间是（）A（0，1）B（1，2）C（2，3）D（3，4）【分析】根据题意，分析函数的定义域，由函数零点的判定定理即可得到结论【解答】解：函数f（x）的定义域为（0，+），且函数f（x）单调递增，f（2）lg2+23lg210，f（3）lg30，在（2，3）内函数f（x）存在零点，故选：C【点评】本题主要考查函数零点存在区间的判断，根据函数的单调性以及函数零点的判断条件是解决本题的关键4
9、（5分）如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是（）ABCD【分析】根据几何体的三视图，得出该几何体的结构特征，从而求出它的体积【解答】解：根据几何体的三视图，得；该几何体是底面为半圆，母线长为2的半圆锥体；且底面半圆的半径为1，该半圆锥个高为2，它的体积为V12故选：C【点评】本题考查了空间几何体的三视图的应用问题，是基础题目5（5分）已知a0.80.7，blog20.7，c1.30.8，则a，b，c的大小关系是（）AabcBbacCcbaDcab【分析】根据指数函数和对数函数的单调性可得答案【解答】解：0a0.80.70.801，
10、blog20.7log210，c1.30.81.301，bac故选：B【点评】本题主要考查指数函数和对数函数的单调性，是基础题6（5分）已知直线l1：x+2my10与直线l2：（m2）xmy+20平行，则实数m的值是（）AB或0CD或0【分析】讨论m0，m2两直线的情况，再由，解方程即可得到所求值【解答】解：直线l1：x+2my10与直线l2：（m2）xmy+20平行，若m0，则两直线为x10，22x0，则重合舍去；若m2时，两直线为x+4y10，22y0，不平行，舍去；即有，解得m，故选：A【点评】本题考查两直线平行的条件，注意讨论直线的斜率不存在的情况，考查运算能力，属于基础题7（5分）如
11、图，长方体ABCDA1B1C1D1中，AA1AB2，AD1，E，F，G分别是DD1，AB，CC1的中点，则异面直线A1E与GF所成角为（）A30B45C60D90【分析】连接B1G，EG，先利用长方形的特点，证明四边形A1B1GE为平行四边形，从而A1EB1G，所以B1GF即为异面直线A1E与GF所成的角，再在三角形B1GF中，分别计算三边的长度，利用勾股定理即可得此角的大小【解答】解：如图：连接B1G，EGE，G分别是DD1，CC1的中点，A1B1EG，A1B1EG，四边形A1B1GE为平行四边形A1EB1G，B1GF即为异面直线A1E与GF所成的角在三角形B1GF中，B1GFGB1FB1G
12、2+FG2B1F2B1GF90异面直线A1E与GF所成角为90故选：D【点评】本题考查了空间异面直线所成的角的作法、证法、算法，长方体的性质及其中的数量关系的应用，将空间问题转化为平面问题的思想方法8（5分）已知圆心（2，1），其一条直径的两个端点恰好在两坐标轴上，则这个圆的方程是（）Ax2+y2+4x2y50Bx2+y24x+2y50Cx2+y2+4x2y0Dx2+y24x+2y0【分析】根据题意，设直径的两个端点分别A（a，0）、B（0，b），由中点坐标公式可得a、b的值，由两点间距离公式计算可得圆的半径，将其代入圆的标准方程即可得答案【解答】解：设直径的两个端点分别A（a，0）、B（0，
13、b），圆心C为点（2，1），由中点坐标公式得，解得a4，b2半径r，圆的方程是：（x+2）2+（y1）25，即x2+y2+4x2y0故选：C【点评】本题考查圆的标准方程，关键是求出直径的两个端点的坐标，求出圆的半径，是中档题9（5分）已知lga+lgb0，函数f（x）ax与函数g（x）logbx的图象可能是（）ABCD【分析】先求出a、b的关系，将函数g（x）进行化简，得到函数f（x）与函数g（x）的单调性是在定义域内同增同减，再进行判定【解答】解：lga+lgb0ab1则b从而g（x）logbxlogax，f（x）ax与函数f（x）与函数g（x）的单调性是在定义域内同增同减结合选项可知选B，
14、故选：B【点评】本题主要考查了对数函数的图象，以及指数函数的图象和对数运算等有关知识，属于基础题10（5分）给出下列命题：如果不同直线m、n都平行于平面，则m、n一定不相交；如果不同直线m、n都垂直于平面，则m、n一定平行；如果平面、互相平行，若直线m，直线n，则mn；如果平面、互相垂直，且直线m、n也互相垂直，若m，则n其中正确的个数为（）A1个B2个C3个D4个【分析】在中，m、n相交、平行或异面；在中，由线面垂直的性质定理得m、n一定平行；在中，m、n相交、平行或异面；在中，n与相交或平行【解答】解：在中，如果不同直线m、n都平行于平面，则m、n相交、平行或异面，故错误；在中，如果不同直
15、线m、n都垂直于平面，则由线面垂直的性质定理得m、n一定平行，故正确；在中，如果平面、互相平行，若直线m，直线n，则m、n相交、平行或异面，故错误；在中，如果平面、互相垂直，且直线m、n也互相垂直，若m，则n与相交或平行，故错误故选：A【点评】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题11（5分）已知圆C：（x3）2+（y4）21和两点A（m，0），B（m，0）（m0），若圆C上存在点P，使得APB90，则m的最大值为（）A7B6C5D4【分析】根据圆心C到O（0，0）的距离为5，可得圆C
16、上的点到点O的距离的最大值为6再由APB90，可得POABm，可得m6，从而得到答案【解答】解：圆C：（x3）2+（y4）21的圆心C（3，4），半径为1，圆心C到O（0，0）的距离为5，圆C上的点到点O的距离的最大值为6再由APB90可得，以AB为直径的圆和圆C有交点，可得POABm，故有m6，故选：B【点评】本题主要直线和圆的位置关系，求得圆C上的点到点O的距离的最大值为6，是解题的关键，属于中档题12（5分）偶函数f（x）（xR）满足：f（5）f（2）0，且在区间0，4与4，+）上分别递增和递减，则不等式xf（x）0的解集为（）A（，5）（2，2）（5，+）B（5，2）（2，5）C（0，
17、2）（5，+）D（5，2）（0，2）（5，+）【分析】根据函数单调性和奇偶性的关系，作出函数的草图，结合不等式的关系进行转化求解即可【解答】解：偶函数f（x）（xR）满足：f（5）f（2）0，且在区间0，4与4，+）上分别递增和递减，函数f（x）对应的图象如图：则不等式xf（x）0等价为或，即或，即0x2或x5或5x2，即不等式的解集为（5，2）（0，2）（5，+），故选：D【点评】本题主要考查不等式的求解，结合函数奇偶性和单调性之间的关系作出函数的图象是解决本题的关键二、填空题（共4小题，每小题5分，满分20分）13（5分）函数f（x）+log2（x+1）的定义域为x|x1且x【分析】函数f
18、（x）+log2（x+1）有意义，可得x+10且2x10，界不大合适即可得到所求定义域【解答】解：函数f（x）+log2（x+1）有意义，可得x+10且2x10，解得x1且x，则定义域为x|x1且x故答案为：x|x1且x【点评】本题考查函数的定义域的求法，注意分式分母不为0和对数的真数大于0，考查运算能力，属于基础题14（5分）已知一个四棱柱，其底面是正方形，侧棱垂直于底面，它的各个顶点都在一个表面积为4cm2的球面上如果该四棱柱的底面边长为1cm，则其侧棱长为cm【分析】球半径为r1cm，设该四棱柱的侧棱长为xm，由该四棱柱的底面边长为1cm，得r1，由此能求出其侧棱长【解答】解：一个四棱柱
19、，其底面是正方形，侧棱垂直于底面，它的各个顶点都在一个表面积为4cm2的球面上球半径为r1cm，设该四棱柱的侧棱长为xm，该四棱柱的底面边长为1cm，r1，解得xcm故答案为：【点评】本题考查四棱柱的侧棱长的求法，考查四棱柱、球等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题15（5分）已知mR，过原点O作圆x2+（m+2）y24x8y16m0的切线，则此时的切线方程为yx或x0【分析】根据圆的方程特点先求出m1，然后求出圆心和半径，结合直线和圆相切的等价条件进行求解即可【解答】解：由圆的方程得m+21，即m1，此时圆的方程为x2+y24x8y+160，
20、即（x2）2+（y4）24，圆心坐标C（2，4），半径为R2，若切线斜率不存在，则x0，圆心到直线x0的距离d2，满足x0与圆相切，若 斜率存在，设ykx，即kxy0，圆心到直线的距离d2，即|k2|，平方得k24k+41+k2，即4k3，得k，则切线方程为yx，综上所述，切线方程为yx或x0，故答案为：yx或x0【点评】本题主要考查直线和圆相切的等价条件，结合圆的方程先求出m是解决本题的关键16（5分）已知函数知f（x）满足对任意x1x2，都有f（x1）f（x2）成立，那么实数a的取值范围是，2）【分析】根据条件判断函数是增函数，结合函数单调性的定义建立不等式关系进行求解即可【解答】解：函数
21、f（x）满足对任意x1x2，都有f（x1）f（x2）成立，函数f（x）在定义域上是增函数，则满足，即，得a2，故答案为：，2）【点评】本题主要考查函数单调性的应用，根据分段函数单调性的性质建立不等式关系是解决本题的关键三、解答题（共6小题，满分70分）17（10分）已知直线l1：（m2）x+my80和直线l2：mx+y30，其中m为常数（）若l1l2，求m的值；（）若点P（1，2m）在l2上，直线l过P点，且在两坐标轴上的截距之和为0，求直线l的方程【分析】（）通过讨论m0或m0的情况，结合直线的垂直关系求出m的值即可；（）求出m的值，求出P的坐标，代入直线方程即可【解答】解：（）若m0，则直
22、线l1：2x80，即x4，l2：y3，直线垂直，符合题意；若m0，则（m）1，解得：m1，综上：m1或0；（）设直线l的方程是：xya，由P（1，2m）在mx+y30上，得：m+2m30，解得：m1，故P（1，2）代入xya，解得：a1，故直线l的方程是：xy+10【点评】本题考查了直线的垂直关系，考查求直线方程问题，是一道中档题18（12分）如图，三棱柱ABCA1B1C1内接于一个圆柱，且底面是正三角形，如果圆柱的体积是2，底面直径与母线长相等（）求该圆柱的侧面积；（）求三棱柱ABCA1B1C1的体积【分析】（）设底面半径为r，则母线长为2r，由V圆柱r22r2，求出r1，由此能求出该圆柱的
23、侧面积（）取AC中点O，连结AD，设底面圆圆心为O，则AOAD1，求出AD，从而求出AB由此能求出三棱柱ABCA1B1C1的体积【解答】解：（）三棱柱ABCA1B1C1内接于一个圆柱，且底面是正三角形，圆柱的体积是2，底面直径与母线长相等设底面半径为r，则母线长为2r，V圆柱r22r2，解得r1，该圆柱的侧面积：S侧2r2r4（）取AC中点O，连结AD，设底面圆圆心为O，则AOAD1，AD，设ABa，则AD，解得a三棱柱ABCA1B1C1的体积：VSABCAA1【点评】本题考查圆柱侧面积的求法，考查三棱柱的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、空间想象
24、能力，考查化归与转化思想、数形结合思想，是中档题19（12分）已知函数f（x）ax+c是R上的奇函数（a，b，c是常数），且满足f（1）3，f（2）（）求a，b，c的值；（）试判断函数f（x）在区间（0，）上的单调性，并用定义证明【分析】（）运用奇函数的定义，可得c0，再由条件得到a，b的方程，解得即可得到解析式；（）运用单调性的定义证明，注意作差、变形、定符号和下结论几个步骤【解答】解：（）函数f（x）ax+c是R上的奇函数，f（x）f（x），故c0，f（1）3，f（2），解得：，故a2，b1，c0；（）由（）f（x）2x+，令0x1x2，则f（x1）f（x2）2x1+2x2（x1x2）（2
25、），0x1x2，x1x20，x1x2，20，故f（x1）f（x2）0，故f（x）在（0，）递减【点评】本题考查函数的奇偶性和单调性的判断和运用，考查运算能力，属于中档题20（12分）如图，在四棱锥PABCD中，ABCD，ABAD，CD2AB，平面PAD底面ABCD，PAADE和F分别是CD和PC的中点，求证：（）BE平面PAD；（）PABC；（）平面BEF平面PCD【分析】（）根据条件，利用平面和平面垂直的性质定理可得PA平面ABCD（）根据已知条件判断ABED为平行四边形，故有BEAD，再利用直线和平面平行的判定定理证得BE平面PAD（）先证明ABED为矩形，可得BECD现证CD平面PAD，
26、可得CDPD，再由三角形中位线的性质可得EFPD，从而证得 CDEF结合利用直线和平面垂直的判定定理证得CD平面BEF，再由平面和平面垂直的判定定理证得平面BEF平面PCD【解答】解：（）PAAD，平面PAD平面ABCD，平面PAD平面ABCDAD，由平面和平面垂直的性质定理可得PA平面ABCD（）ABCD，ABAD，CD2AB，E和F分别是CD和PC的中点，故四边形ABED为平行四边形，故有BEAD又AD平面PAD，BE不在平面PAD内，故有BE平面PAD（）平行四边形ABED中，由ABAD可得，ABED为矩形，故有BECD由PA平面ABCD，可得PAAB，再由ABAD可得AB平面PAD，C
27、D平面PAD，故有CDPD再由E、F分别为CD和PC的中点，可得EFPD，CDEF而EF和BE是平面BEF内的两条相交直线，故有CD平面BEF由于CD平面PCD，平面BEF平面PCD【点评】题主要考查直线和平面垂直的判定定理，直线和平面平行的判定定理，平面和平面垂直的判定定理、性质定理的应用，属于中档题21（12分）已知圆C的圆心为点C（0，3），点D（，2）在圆C上，直线l过点A（1，0）且与圆C相交P，Q两点，点M是线段PQ的中点（1）求圆C的方程：（2）若|AM|3，求直线l的方程【分析】（1）可得圆的半径R即可得圆C的方程为：x2+（y3）24，（2）设点M（x，y），由|AM|3，（
28、x+1）2+y29，点M是线段PQ的中点，即1，y23y+x2+x0，由得x+3y80，从而可得答案【解答】解：（1）圆C的圆心为点C（0，3），点D（，2）在圆C上，圆的半径R圆C的方程为：x2+（y3）24，（2）点M是线段PQ的中点，AMCM，可得AM2+d2R2，当直线l的斜率为k时，设方程为kxy+k0d 解得k，即直线l的方程为：4x3y+40，当直线l的斜率不存在时，直线x1符合题意综上所述：直线l的方程为：4x3y+40或x1【点评】本题考查了圆的方程、直线与圆的位置关系，属于中档题22（12分）已知函数ylog2（4x+1）kx是偶函数，g（x）log2（a2xa）（其中a0
29、）（）求g（x）的定义域；（）求k的值；（）若函数f（x）与g（x）的图象有且只有一个交点，求a的取值范围【分析】（）根据对数函数的性质求出函数的定义域即可；（）直接根据函数的奇偶性列式求出k的值；（）运用函数与方程思想解题，问题转化为关于t的方程（a1）t2at10在（，+）上只有一解【解答】解：（）由a2xa0得：2x0，解得：xlog2，故函数的定义域是（log2，+）；（）f（x）log2（4x+1）kx （kR）是偶函数，f（x）log2（4x+1）+kxf（x）对任意xR恒成立，log2（4x+1）2x+kxlog2（4x+1）kx恒成立，则2（k1）x0恒成立，因此，
30、k1；（）由于a0，所以g（x）log2（a2xa）定义域为（log2，+），也就是满足2x，函数f（x）与g（x）的图象有且只有一个交点，方程log2（4x+1）xlog2（a2xa）在（log2，+）上只有一解即：方程a2xa在（log2，+）上只有一解，令2xt，则t，因而问题等价为：关于t的方程（a1）t2at10（*）在（，+）上只有一解，当a1时，解得t（，+），不合题意；当0a1时，记h（t）（a1）t2at1，其图象的对称轴t0，函数f（2mmcos）+f（1sin2）f（0）在（0，+）上递减，而h（0）1，方程（*）在（，+）无解；当a1时，记h（t）（a1）t2at1，其图象的对称轴t0，h（0）1， 所以，只需h（）0，即（a1）a10，此恒成立，此时a的范围为a1，综上所述，所求a的取值范围为a1【点评】本题主要考查了函数奇偶性的应用，运用对数函数的单调性解不等式，以及函数图象交点的确定，属于中档题
