1、函数与几何综合 1如图，抛物线C1：yx22x与抛物线C2：yax2+bx开口大小相同、方向相反，它们相交于O，C两点，且分别与x轴的正半轴交于点B，点A，OA2OB（1）求抛物线C2的解析式；（2）在抛物线C2的对称轴上是否存在点P，使PA+PC的值最小？若存在，求出点P的坐标，若不存在，说明理由；（3）M是直线OC上方抛物线C2上的一个动点，连接MO，MC，M运动到什么位置时，MOC面积最大？并求出最大面积2如图，抛物线yx2+bx+c与直线yx+3分别相交于A，B两点，且此抛物线与x轴的一个交点为C，连接AC，BC已知A（0，3），C（3，0）（1）求抛物线的解析式；（2）在抛物线对称轴
2、l上找一点M，使|MBMC|的值最大，并求出这个最大值；（3）点P为y轴右侧抛物线上一动点，连接PA，过点P作PQPA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由3如图，已知抛物线yax2+bx1与x轴的交点为A（1，0），B（2，0），且与y轴交于C点（1）求该抛物线的表达式；（2）点C关于x轴的对称点为C1，M是线段BC1上的一个动点（不与B、C1重合），MEx轴，MFy轴，垂足分别为E、F，当点M在什么位置时，矩形MFOE的面积最大？说明理由（3）已知点P是直线yx+1上的动点，点Q为抛物线上的动点
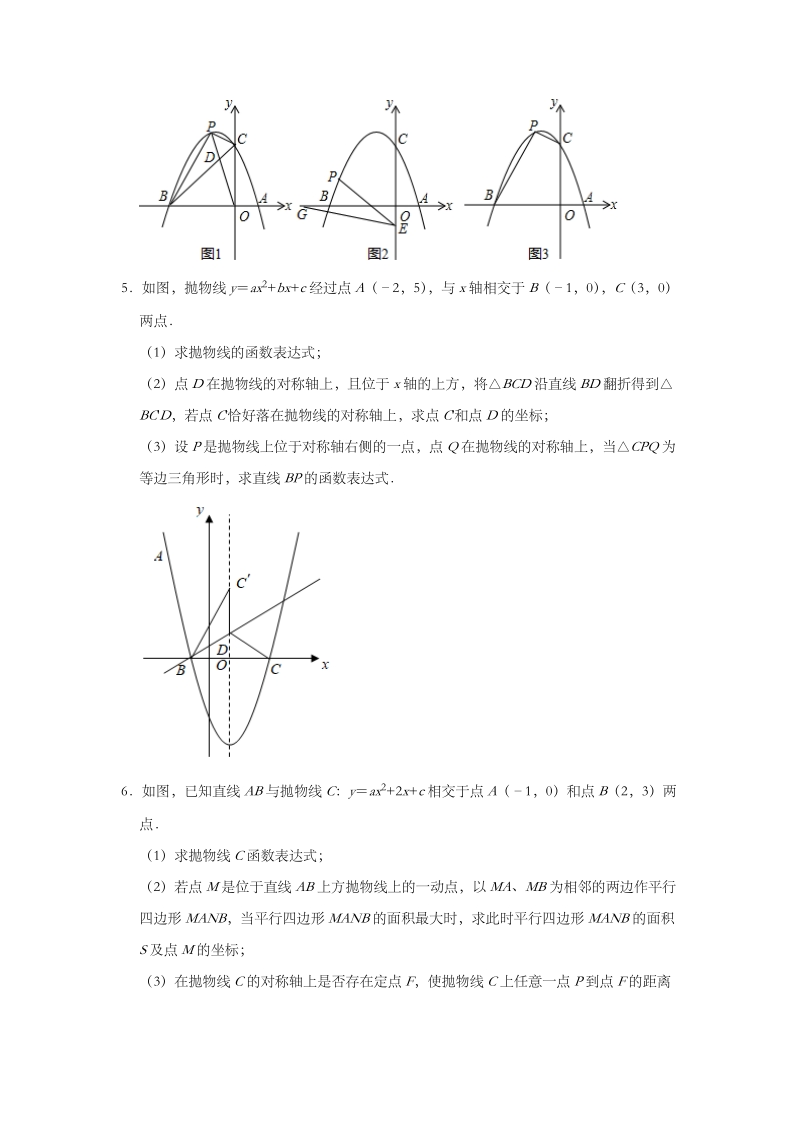
3、，当以C、C1、P、Q为顶点的四边形为平行四边形时，求出相应的点P和点Q的坐标4已知抛物线yax2+bx+3经过点A（1，0）和点B（3，0），与y轴交于点C，点P为第二象限内抛物线上的动点（1）抛物线的解析式为 ，抛物线的顶点坐标为 ；（2）如图1，连接OP交BC于点D，当SCPD：SBPD1：2时，请求出点D的坐标；（3）如图2，点E的坐标为（0，1），点G为x轴负半轴上的一点，OGE15，连接PE，若PEG2OGE，请求出点P的坐标；（4）如图3，是否存在点P，使四边形BOCP的面积为8？若存在，请求出点P的坐标；若不存在，请说明理由5如图，抛物线yax2+bx+c经过点A（2，5），与
4、x轴相交于B（1，0），C（3，0）两点（1）求抛物线的函数表达式；（2）点D在抛物线的对称轴上，且位于x轴的上方，将BCD沿直线BD翻折得到BCD，若点C恰好落在抛物线的对称轴上，求点C和点D的坐标；（3）设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当CPQ为等边三角形时，求直线BP的函数表达式6如图，已知直线AB与抛物线C：yax2+2x+c相交于点A（1，0）和点B（2，3）两点（1）求抛物线C函数表达式；（2）若点M是位于直线AB上方抛物线上的一动点，以MA、MB为相邻的两边作平行四边形MANB，当平行四边形MANB的面积最大时，求此时平行四边形MANB的面积S及点M的
5、坐标；（3）在抛物线C的对称轴上是否存在定点F，使抛物线C上任意一点P到点F的距离等于到直线y的距离？若存在，求出定点F的坐标；若不存在，请说明理由7已知抛物线yx2+bx+c的对称轴为直线x1，其图象与x轴相交于A，B两点，与y轴相交于点C（0，3）（1）求b，c的值；（2）直线1与x轴相交于点P如图1，若ly轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x1的对称点为点D，求四边形CEDF面积的最大值；如图2，若直线1与线段BC相交于点Q，当PCQCAP时，求直线1的表达式8如图，在平面直角坐标系xOy中，已知二次函数yax2+bx+c的图象经过点A（2，0），C（0，6），其对
6、称轴为直线x2（1）求该二次函数的解析式；（2）若直线yx+m将AOC的面积分成相等的两部分，求m的值；（3）点B是该二次函数图象与x轴的另一个交点，点D是直线x2上位于x轴下方的动点，点E是第四象限内该二次函数图象上的动点，且位于直线x2右侧若以点E为直角顶点的BED与AOC相似，求点E的坐标9在平面直角坐标系中，将二次函数yax2（a0）的图象向右平移1个单位，再向下平移2个单位，得到如图所示的抛物线，该抛物线与x轴交于点A、B（点A在点B的左侧），OA1，经过点A的一次函数ykx+b（k0）的图象与y轴正半轴交于点C，且与抛物线的另一个交点为D，ABD的面积为5（1）求抛物线和一次函数的
7、解析式；（2）抛物线上的动点E在一次函数的图象下方，求ACE面积的最大值，并求出此时点E的坐标；（3）若点P为x轴上任意一点，在（2）的结论下，求PE+PA的最小值10如图，直线yx+4与x轴，y轴分别交于A，B两点，过A，B两点的抛物线yax2+bx+c与x轴交于点C（1，0）（1）求抛物线的解析式；（2）连接BC，若点E是线段AC上的一个动点（不与A，C重合），过点E作EFBC，交AB于点F，当BEF的面积是时，求点E的坐标；（3）在（2）的结论下，将BEF绕点F旋转180得BEF，试判断点E是否在抛物线上，并说明理由11如图，顶点为P（3，3）的二次函数图象与x轴交于点A（6，0），点B
8、在该图象上，OB交其对称轴l于点M，点M、N关于点P对称，连接BN、ON（1）求该二次函数的关系式（2）若点B在对称轴l右侧的二次函数图象上运动，请解答下列问题：连接OP，当OPMN时，请判断NOB的形状，并求出此时点B的坐标求证：BNMONM12两条抛物线C1：y13x26x1与C2：y2x2mx+n的顶点相同（1）求抛物线C2的解析式；（2）点A是抛物线C2在第四象限内图象上的一动点，过点A作APx轴，P为垂足，求AP+OP的最大值；（3）设抛物线C2的顶点为点C，点B的坐标为（1，4），问在C2的对称轴上是否存在点Q，使线段QB绕点Q顺时针旋转90得到线段QB，且点B恰好落在抛物线C2上
9、？若存在，求出点Q的坐标；若不存在，请说明理由13如图，已知抛物线ya（x+2）（x6）与x轴相交于A、B两点，与y轴交于C点，且tanCAB设抛物线的顶点为M，对称轴交x轴于点N（1）求抛物线的解析式；（2）P为抛物线的对称轴上一点，Q（n，0）为x轴上一点，且PQPC当点P在线段MN（含端点）上运动时，求n的变化范围；在的条件下，当n取最大值时，求点P到线段CQ的距离；在的条件下，当n取最大值时，将线段CQ向上平移t个单位长度，使得线段CQ与抛物线有两个交点，求t的取值范围14如图，抛物线yax2+bx+c与x轴交于点A（1，0），点B（3，0），且OBOC（1）求抛物线的解析式；（2）点
10、P在抛物线上，且POBACB，求点P的坐标；（3）抛物线上两点M，N，点M的横坐标为m，点N的横坐标为m+4点D是抛物线上M，N之间的动点，过点D作y轴的平行线交MN于点E求DE的最大值；点D关于点E的对称点为F，当m为何值时，四边形MDNF为矩形15如图1，在平面直角坐标系中，抛物线yx2+bx+c经过点A（5，0）和点B（1，0）（1）求抛物线的解析式及顶点D的坐标；（2）点P是抛物线上A、D之间的一点，过点P作PEx轴于点E，PGy轴，交抛物线于点G，过点G作GFx轴于点F，当矩形PEFG的周长最大时，求点P的横坐标；（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作D
11、MNDBA，MN交线段AD于点N，是否存在这样点M，使得DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由16如图，在平面直角坐标系xOy中，已知抛物线yax22x+c与直线ykx+b都经过A（0，3）、B（3，0）两点，该抛物线的顶点为C（1）求此抛物线和直线AB的解析式；（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；（3）设点P是直线AB下方抛物线上的一动点，当PAB面积最大时，求点P的坐标，并求PAB面积的最大值17如图，抛物线yx2
12、+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：ykx+n与y轴交于点C，与抛物线yx2+bx+c的另一个交点为D，已知A（1，0），D（5，6），P点为抛物线yx2+bx+c上一动点（不与A、D重合）（1）求抛物线和直线l的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PEx轴交直线l于点E，作PFy轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由18如图1，已知抛物线yx2+bx+c过点A（1，0），B（3，0）（1）求抛
13、物线的解析式及其顶点C的坐标；（2）设点D是x轴上一点，当tan（CAO+CDO）4时，求点D的坐标；（3）如图2抛物线与y轴交于点E，点P是该抛物线上位于第二象限的点，线段PA交BE于点M，交y轴于点N，BMP和EMN的面积分别为m、n，求mn的最大值19如图，抛物线yax2+bx5（a0）经过x轴上的点A（1，0）和点B及y轴上的点C，经过B、C两点的直线为yx+n求抛物线的解析式点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC上以每秒2个单位的速度向C运动当其中一个点到达终点时，另一点也停止运动设运动时间为t秒，求t为何值时，PBE的面积最大并求出最大
14、值过点A作AMBC于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标20如图，抛物线yx2+bx+c过点A（3，2），且与直线yx+交于B、C两点，点B的坐标为（4，m）（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点，过点D作DEx轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值；（3）设点M为抛物线的顶点，在y轴上是否存在点Q，使AQM45？若存在，求点Q的坐标；若不存在，请说明理由21如图，抛物线yax2+bx+c的图象过点A（1，0）、B（3
15、，0）、C（0，3）（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P，使得PAC的周长最小，若存在，请求出点P的坐标及PAC的周长；若不存在，请说明理由；（3）在（2）的条件下，在x轴上方的抛物线上是否存在点M（不与C点重合），使得SPAMSPAC？若存在，请求出点M的坐标；若不存在，请说明理由22已知二次函数yax2bx+c且ab，若一次函数ykx+4与二次函数的图象交于点A（2，0）（1）写出一次函数的解析式，并求出二次函数与x轴交点坐标；（2）当ac时，求证：直线ykx+4与抛物线yax2bx+c一定还有另一个异于点A的交点；（3）当cac+3时，求出直线ykx+4与抛物线
16、yax2bx+c的另一个交点B的坐标；记抛物线顶点为M，抛物线对称轴与直线ykx+4的交点为N，设SSAMNSBMN，写出S关于a的函数，并判断S是否有最大值？如果有，求出最大值；如果没有，请说明理由23如图，在平面直角坐标系中，已知抛物线yax2+bx+2（a0）与x轴交于A（1，0），B（3，0）两点，与y轴交于点C，连接BC（1）求该抛物线的解析式，并写出它的对称轴；（2）点D为抛物线对称轴上一点，连接CD、BD，若DCBCBD，求点D的坐标；（3）已知F（1，1），若E（x，y）是抛物线上一个动点（其中1x2），连接CE、CF、EF，求CEF面积的最大值及此时点E的坐标（4）若点N为抛
17、物线对称轴上一点，抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由24如图，直线yx+3与x轴、y轴分别交于B、C两点，抛物线yx2+bx+c经过点B、C，与x轴另一交点为A，顶点为D（1）求抛物线的解析式；（2）在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值；（3）在抛物线的对称轴上是否存在一点P，使得APBOCB？若存在，求出P点坐标；若不存在，请说明理由25已知，如图，抛物线yax2+bx+c（a0）的顶点为M（1，9），经过抛物线上的两点A（3，7）和B（3，m）的直线交抛物线的对称轴于
18、点C（1）求抛物线的解析式和直线AB的解析式（2）在抛物线上A、M两点之间的部分（不包含A、M两点），是否存在点D，使得SDAC2SDCM？若存在，求出点D的坐标；若不存在，请说明理由（3）若点P在抛物线上，点Q在x轴上，当以点A，M，P，Q为顶点的四边形是平行四边形时，直接写出满足条件的点P的坐标26如图，抛物线yax2+bx2（a0）与x轴交于A（3，0），B（1，0）两点，与y轴交于点C，直线yx与该抛物线交于E，F两点（1）求抛物线的解析式（2）P是直线EF下方抛物线上的一个动点，作PHEF于点H，求PH的最大值（3）以点C为圆心，1为半径作圆，C上是否存在点M，使得BCM是以CM为直
19、角边的直角三角形？若存在，直接写出M点坐标；若不存在，说明理由27如图，已知二次函数yx2+bx+c的图象与x轴交于点A（1，0）、B（3，0），与y轴交于点C（1）求二次函数的解析式；（2）若点P为抛物线上的一点，点F为对称轴上的一点，且以点A、B、P、F为顶点的四边形为平行四边形，求点P的坐标；（3）点E是二次函数第四象限图象上一点，过点E作x轴的垂线，交直线BC于点D，求四边形AEBD面积的最大值及此时点E的坐标28二次函数yax2+bx+2的图象交x轴于点（1，0），B（4，0）两点，交y轴于点C动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MNx轴交直线BC于点N
20、，交抛物线于点D，连接AC，设运动的时间为t秒（1）求二次函数yax2+bx+2的表达式；（2）连接BD，当t时，求DNB的面积；（3）在直线MN上存在一点P，当PBC是以BPC为直角的等腰直角三角形时，求此时点D的坐标；（4）当t时，在直线MN上存在一点Q，使得AQC+OAC90，求点Q的坐标29如图，抛物线yax2+bx+4交x轴于A（3，0），B（4，0）两点，与y轴交于点C，连接AC，BC点P是第一象限内抛物线上的一个动点，点P的横坐标为m（1）求此抛物线的表达式；（2）过点P作PMx轴，垂足为点M，PM交BC于点Q试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三
21、角形是等腰三角形若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PNBC，垂足为点N请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？30如图，已知抛物线yax2+bx+c经过点A（3，0）、B（9，0）和C（0，4），CD垂直于y轴，交抛物线于点D，DE垂直于x轴，垂足为E，直线l是该抛物线的对称轴，点F是抛物线的顶点（1）求出该二次函数的表达式及点D的坐标；（2）若RtAOC沿x轴向右平移，使其直角边OC与对称轴l重合，再沿对称轴l向上平移到点C与点F重合，得到RtA1O1F，求此时RtA1O1F与矩形OCDE重叠部分图形的面积；（3）若Rt
22、AOC沿x轴向右平移t个单位长度（0t6）得到RtA2O2C2，RtA2O2C2与RtOED重叠部分图形的面积记为S，求S与t之间的函数表达式，并写出自变量t的取值范围31如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点A（1，0）、B（5，0）、C（0，4）三点（1）求抛物线的解析式和对称轴；（2）P是抛物线对称轴上的一点，求满足PA+PC的值为最小的点P坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由（请在图2中探索）32设二次函数y（xx1）（xx2）（x1，x2
23、是实数）（1）甲求得当x0时，y0；当x1时，y0；乙求得当x时，y若甲求得的结果都正确，你认为乙求得的结果正确吗？说明理由（2）写出二次函数图象的对称轴，并求该函数的最小值（用含x1，x2的代数式表示）（3）已知二次函数的图象经过（0，m）和（1，n）两点（m，n是实数），当0x1x21时，求证：0mn参考答案与试题解析一解答题（共32小题）1【分析】（1）C1、C2：yax2+bx开口大小相同、方向相反，则a1，将点A的坐标代入C2的表达式，即可求解；（2）作点C关于C1对称轴的对称点C（1，3），连接AC交函数C2的对称轴与点P，此时PA+PC的值最小，即可求解；（3）SMOCMHxC（
24、x2+4xx）x2+，即可求解【解答】解：（1）令：yx22x0，则x0或2，即点B（2，0），C1、C2：yax2+bx开口大小相同、方向相反，则a1，则点A（4，0），将点A的坐标代入C2的表达式得：016+4b，解得：b4，故抛物线C2的解析式为：yx2+4x；（2）联立C1、C2表达式并解得：x0或3，故点C（3，3），作点C关于C2对称轴的对称点C（1，3），连接AC交函数C2的对称轴与点P，此时PA+PC的值最小为：线段AC的长度3，此时点P（2，2）；（3）直线OC的表达式为：yx，过点M作y轴的平行线交OC于点H，设点M（x，x2+4x），则点H（x，x），则SMOCMHxC（
25、x2+4xx）x2+x，0，故x，SMOC最大值为【点评】此题考查了待定系数法求解析式，还考查了三角形的面积，要注意将三角形分解成两个三角形求解；还要注意求最大值可以借助于二次函数2【分析】（1）将A（0，3），C（3，0）代入yx2+bx+c，即可求解；（2）分当点B、C、M三点不共线时、当点B、C、M三点共线时，两种情况分别求解即可；（3）分当时、当时两种情况，分别求解即可【解答】解：（1）将A（0，3），C（3，0）代入yx2+bx+c得：，解得：，抛物线的解析式是yx2+x+3；（2）将直线yx+3表达式与二次函数表达式联立并解得：x0或4，A （0，3），B（4，1）当点B、C、M三
26、点不共线时，|MBMC|BC当点B、C、M三点共线时，|MBMC|BC当点、C、M三点共线时，|MBMC|取最大值，即为BC的长，过点B作x轴于点E，在RtBEC中，由勾股定理得BC，|MBMC|取最大值为；（3）存在点P使得以A、P、Q为顶点的三角形与ABC相似设点P坐标为（x，x2+x+3）（x0）在RtBEC中，BECE1，BCE45，在RtACO中，AOCO3，ACO45，ACB180450450900，AC3，过点P作PQPA于点P，则APQ90，过点P作PQy轴于点G，PQAAPQ90PAGQAP，PGAQPAPGAACB90当时，PAGBAC，解得x11，x20，（舍去）点P的纵
27、坐标为12+1+36，点P为（1，6）；当时，PAGABC，3，解得x1（舍去），x20（舍去），此时无符合条件的点P综上所述，存在点P（1，6）【点评】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似、勾股定理运用等知识点，其中（2）、（3），要注意分类求解，避免遗漏3【分析】（1）待定系数法将已知点的坐标分别代入得方程组并解方程组即可求得抛物线的表达式；（2）先求得C1（0，1），再由待定系数法求得直线C1B解析式yx+1，设M（t，+1），得S矩形MFOEOEOFt（t+1）（t1）2+，由二次函数性质即可得到结论；（3）以C、C1、P、Q为顶点的四边形为平行四边形要分两种情况进
28、行讨论：C1C为边，C1C为对角线【解答】解：（1）将A（1，0），B（2，0）分别代入抛物线yax2+bx1中，得，解得：该抛物线的表达式为：yx2x1（2）在yx2x1中，令x0，y1，C（0，1）点C关于x轴的对称点为C1，C1（0，1），设直线C1B解析式为ykx+b，将B（2，0），C1（0，1）分别代入得，解得，直线C1B解析式为yx+1，设M（t，+1），则 E（t，0），F（0，+1）S矩形MFOEOEOFt（t+1）（t1）2+，0，当t1时，S矩形MFOE最大值，此时，M（1，）；即点M为线段C1B中点时，S矩形MFOE最大（3）由题意，C（0，1），C1（0，1），以C、
29、C1、P、Q为顶点的四边形为平行四边形，分以下两种情况：C1C为边，则C1CPQ，C1CPQ，设P（m，m+1），Q（m，m1），|（m1）（m+1）|2，解得：m14，m22，m32，m40（舍），P1（4，3），Q1（4，5）；P2（2，0），Q2（2，2）；P3（2，2），Q3（2，0）C1C为对角线，C1C与PQ互相平分，C1C的中点为（0，0），PQ的中点为（0，0），设P（m，m+1），则Q（m，+m1）（m+1）+（+m1）0，解得：m10（舍去），m22，P4（2，0），Q4（2，0）；综上所述，点P和点Q的坐标为：P1（4，3），Q1（4，5）或P2（2，0），Q2（2，2）
30、或P3（2，2），Q3（2，0）或P4（2，0），Q4（2，0）【点评】本题属于中考压轴题类型，主要考查了待定系数法求一次函数、二次函数解析式，二次函数的最值运用，平行四边形性质等，解题关键要正确表示线段的长度，掌握分类讨论的方法4【分析】（1）函数的表达式为：ya（x1）（x+3）a（x2+2x3），即可求解；（2）SCPD：SBPD1：2，则BDBC2，即可求解；（3）OGE15，PEG2OGE30，则OHE45，故OHOE1，即可求解；（4）利用S四边形BOCPSOBC+SPBC8，即可求解【解答】解：（1）函数的表达式为：ya（x1）（x+3）a（x2+2x3），即：3a3，解得：a1
31、，故抛物线的表达式为：yx22x+3，顶点坐标为（1，4）；（2）OBOC，CBO45，SCPD：SBPD1：2，BDBC2，yDBDsinCBO2，则点D（1，2）；（3）如图2，设直线PE交x轴于点H，OGE15，PEG2OGE30，OHE45，OHOE1，则直线HE的表达式为：yx1，联立并解得：x（舍去正值），故点P（，）；（4）不存在，理由：连接BC，过点P作y轴的平行线交BC于点H，直线BC的表达式为：yx+3，设点P（x，x22x+3），点H（x，x+3），则S四边形BOCPSOBC+SPBC33+（x22x+3x3）38，整理得：3x2+9x+70，解得：0，故方程无解，则不存
32、在满足条件的点P【点评】本题考查的是二次函数综合运用，涉及到一次函数、一元二次方程应用、图象的面积计算等，难度不大5【分析】（1）根据待定系数法，把点A（2，5），B（1，0），C（3，0）的坐标代入yax2+bx+c得到方程组求解即可；（2）设抛物线的对称轴与x轴交于点H，则H点的坐标为（1，0），BH2，由翻折得CBCB4，求出CH的长，可得CBH60，求出DH的长，则D坐标可求；（3）由题意可知CCB为等边三角形，分两种情况讨论：当点P在x轴的上方时，点Q在x轴上方，连接BQ，CP证出BCQCCP，可得BP垂直平分CC，则D点在直线BP上，可求出直线BP的解析式，当点P在x轴的下方时，点
33、Q在x轴下方同理可求出另一直线解析式【解答】解：（1）由题意得：解得，抛物线的函数表达式为yx22x3（2）抛物线与x轴交于B（1，0），C（3，0），BC4，抛物线的对称轴为直线x1，如图，设抛物线的对称轴与x轴交于点H，则H点的坐标为（1，0），BH2，由翻折得CBCB4，在RtBHC中，由勾股定理，得CH2，点C的坐标为（1，2），tan，CBH60，由翻折得DBHCBH30，在RtBHD中，DHBHtanDBH2tan30，点D的坐标为（1，）（3）取（2）中的点C，D，连接CC，BCBC，CBC60，CCB为等边三角形分类讨论如下：当点P在x轴的上方时，点Q在x轴上方，连接BQ，CP
34、PCQ，CCB为等边三角形，CQCP，BCCC，PCQCCB60，BCQCCP，BCQCCP（SAS），BQCP点Q在抛物线的对称轴上，BQCQ，CPCQCP，又BCBC，BP垂直平分CC，由翻折可知BD垂直平分CC，点D在直线BP上，设直线BP的函数表达式为ykx+b，则，解得，直线BP的函数表达式为y当点P在x轴的下方时，点Q在x轴下方PCQ，CCB为等边三角形，CPCQ，BCCC，CCBQCPCCB60BCPCCQ，BCPCCQ（SAS），CBPCCQ，BCCC，CHBC，CBP30，设BP与y轴相交于点E，在RtBOE中，OEOBtanCBPOBtan301，点E的坐标为（0，）设直线
35、BP的函数表达式为ymx+n，则，解得，直线BP的函数表达式为y综上所述，直线BP的函数表达式为或【点评】本题考查了二次函数的综合题，涉及的知识点有：待定系数法求二次函数解析式，待定系数法求一次函数解析式，轴对称的性质，全等三角形的判定和性质，等边三角形的判定与性质，锐角三角函数等知识，综合性较强，有一定的难度6【分析】（1）利用待定系数法，将A，B的坐标代入yax2+2x+c即可求得二次函数的解析式；（2）过点M作MHx轴于H，交直线AB于K，求出直线AB的解析式，设点M（a，a2+2a+3），则K（a，a+1），利用函数思想求出MK的最大值，再求出AMB面积的最大值，可推出此时平行四边形M
36、ANB的面积S及点M的坐标；（3）如图2，分别过点B，C作直线y的垂线，垂足为N，H，设抛物线对称轴上存在点F，使抛物线C上任意一点P到点F的距离等于到直线y的距离，其中F（1，a），连接BF，CF，则可根据BFBN，CFCN两组等量关系列出关于a的方程组，解方程组即可【解答】解：（1）由题意把点（1，0）、（2，3）代入yax2+2x+c，得，解得a1，c3，此抛物线C函数表达式为：yx2+2x+3；（2）如图1，过点M作MHx轴于H，交直线AB于K，将点（1，0）、（2，3）代入ykx+b中，得，解得，k1，b1，yABx+1，设点M（a，a2+2a+3），则K（a，a+1），则MKa2+
37、2a+3（a+1）（a）2+，根据二次函数的性质可知，当a时，MK有最大长度，SAMB最大SAMK+SBMKMKAH+MK（xBxH）MK（xBxA）3，以MA、MB为相邻的两边作平行四边形MANB，当平行四边形MANB的面积最大时，S最大2SAMB最大2，M（，）；（3）存在点F，yx2+2x+3（x1）2+4，对称轴为直线x1，当y0时，x11，x23，抛物线与点x轴正半轴交于点C（3，0），如图2，分别过点B，C作直线y的垂线，垂足为N，H，抛物线对称轴上存在点F，使抛物线C上任意一点P到点F的距离等于到直线y的距离，设F（1，a），连接BF，CF，则BFBN3，CFCH，由题意可列：，
38、解得，a，F（1，）【点评】此题考查了待定系数法求解析式，还考查了用函数思想求极值等，解题关键是能够判断出当平行四边形MANB的面积最大时，ABM的面积最大，且此时线段MK的长度也最大7【分析】（1）根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值；（2）由题意先求出D点坐标为（2，3），求出直线AC的解析式，设F（a，a2+2a+3），E（a，a+3），则EFa2+3a，四边形CEDF的面积可表示为，利用二次函数的性质可求出面积的最大值；（3）当PCQCAP时，可得PCACPQ，PACPCQOCA45，则PQAC，BCOPCA，过点P作PMAC交AC于点M，可求出PM、PA、OP的
39、长，用待定系数法可求出函数解析式【解答】解：（1）由题意得：，b2，c3，（2）如图1，点C关于直线x1的对称点为点D，CDOA，3x2+2x+3，解得：x10，x22，D（2，3），抛物线的解析式为yx2+2x+3，令y0，解得x11，x23，B（1，0），A（3，0），设直线AC的解析式为ykx+b，解得：，直线AC的解析式为yx+3，设F（a，a2+2a+3），E（a，a+3），EFa2+2a+3+a3a2+3a，四边形CEDF的面积SEFC+SEFDa2+3a，当a时，四边形CEDF的面积有最大值，最大值为当PCQCAP时，PCACPQ，PACPCQ，PQAC，C（0，3），A（3，0
40、），OAOC，OCAOACPCQ45，BCOPCA，如图2，过点P作PMAC交AC于点M，设PMb，则CM3b，AMb，设直线l的解析式为yx+n，直线l的解析式为yx+【点评】本题考查了二次函数的综合题：熟练掌握二次函数的性质和轴对称的性质；会利用待定系数法求函数解析式；理解坐标与图形性质，会利用相似三角形的性质解题；要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度是解题的关键8【分析】（1）把点A、C坐标及对称轴x2代入二次函数表达式，即可求解；（2）求出直线yx+m与y轴的交点为（0，m），由SAOC6，3，即可求解；（3）分DEOAOC、BEDAOC两种
41、情况，分别求解即可【解答】解：（1）由已知得：，解得：，故抛物线的表达式为：yx22x6，同理可得直线AC的表达式为：y3x6；（2）联立，解得：x，直线yx+m与y轴的交点为（0，m），SAOC6，由题意得：3，解得：m2或10（舍去10），m2；（3）OA2，OC6，当DEBAOC时，则，如图1，过点E作EF直线x2，垂足为F，过点B作BGEF，垂足为G，则RtBEGRtEDF，则，则BG3EF，设点E（h，k），则BGk，FEh2，则k3（h2），即k63h，点E在二次函数上，故：h22h663h，解得：h4或6（舍去6），则点E（4，6）；当BEDAOC时，过点E作ME直线x2，垂足为
42、M，过点B作BNME，垂足为N，则RtBENRtEDM，则，则NBEM，设点E（p，q），则BNq，EMp2，则q（p2），解得：p或（舍去）；故点E坐标为（4，6）或（，）【点评】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似等知识点，其中（3），要注意分类求解，避免遗漏9【分析】（1）先写出平移后的抛物线解析式，经过点A（1，0），可求得a的值，由ABD的面积为5可求出点D的纵坐标，代入抛物线解析式求出横坐标，由A、D的坐标可求出一次函数解析式；（2）作EMy轴交AD于M，如图，利用三角形面积公式，由SACESAMESCME构建二次函数，利用二次函数的性质即可解决问题；（3）作E关于x轴的对称点F，过点F作FHAE于点H，交x轴于点P，则BAEHAPHFE，利用锐角三角函数的定义可得出EP+APFP+HP，此时FH最小，求出最小值即可【解答】解：（1）将二次函数yax2（a0）的图象向右平移1个单位，再向下平移2个单位，得到的抛物线解析式为ya（x1）22，OA1，点A的坐标为（1，0），代入抛物线的解析式得，4a20，抛物线的解析式为
