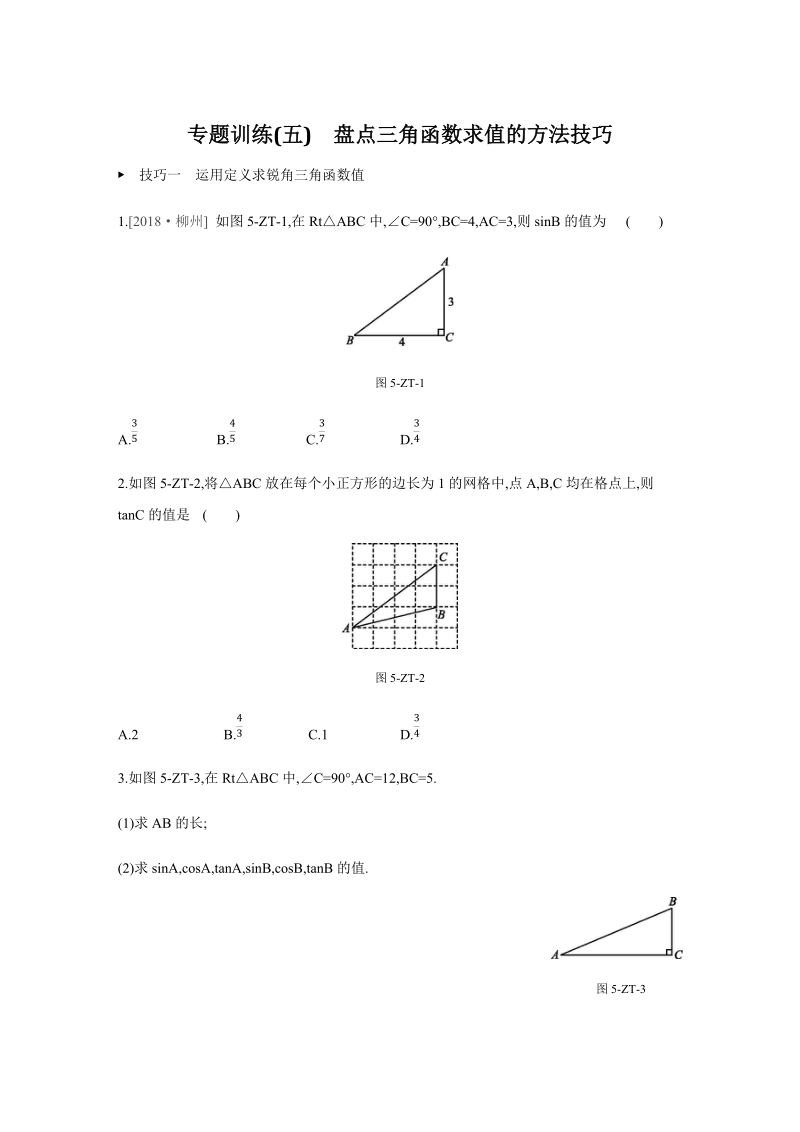
1、专题训练(五)盘点三角函数求值的方法技巧技巧一运用定义求锐角三角函数值1.2018柳州 如图5-ZT-1,在RtABC中,C=90,BC=4,AC=3,则sinB的值为()图5-ZT-1A.35 B.45 C.37 D.342.如图5-ZT-2,将ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanC的值是()图5-ZT-2A.2 B.43 C.1 D.343.如图5-ZT-3,在RtABC中,C=90,AC=12,BC=5.(1)求AB的长;(2)求sinA,cosA,tanA,sinB,cosB,tanB的值.图5-ZT-34.如图5-ZT-4,在ABC中,AB=8,
2、BC=6,SABC=12.试求 tanB的值.图5-ZT-4技巧二巧设参数求锐角三角函数值5.在RtABC中,C=90,若tanA=512,则cosA的值是()A.512 B.813 C.23 D.12136.在ABC中,若ACBCAB=51213,则 cosA的值为()A.1213 B.513 C.512 D.1257.已知为锐角,且cos=13,求sin和tan的值.8.如图5-ZT-5,在ABC中,ACB=90,CDAB于点D,BEAB=35,若CE=2,cosACD=45,求tanAEC的值及CD的长.图5-ZT-5技巧三利用边角关系求锐角三角函数值9.如图5-ZT-6,在四边形ABC
3、D中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则tanC的值为()图5-ZT-6A.34 B.43 C.35 D.4510.如图5-ZT-7,在22的正方形网格中,有以格点为顶点的ABC,则sinCAB的值为()图5-ZT-7A.323 B.35 C.105 D.31011.如图5-ZT-8,在RtABC中,ACB=90,AC等于AB边上的中线CD的32,求sinB的值.图5-ZT-8技巧四利用等角求锐角三角函数值12.如图5-ZT-9,在ABC中,AB=AC=5,BC=8.若BPC=12BAC,则tanBPC=.图5-ZT-913.如图5-ZT-10,在ABC中,ACB
4、=90,CDAB于点D,AC=8,AB=10,求cosBCD的值.图5-ZT-1014.如图5-ZT-11,已知AB是O的直径,CD是弦且CDAB,BC=6,AC=8,求sinABD的值.图5-ZT-11教师详解详析1.A解析 由勾股定理,得AB=AC2+BC2=32+42=5.根据正弦的定义,得sinB=ACAB=35.2.B解析 如图,在RtACD中,tanC=ADCD=43.故选B.3.解:(1)AB=AC2+BC2=13.(2)sinA=BCAB=513,cosA=ACAB=1213,tanA=BCAC=512,sinB=ACAB=1213,cosB=BCAB=513,tanB=ACB
5、C=125.4.解:如图,过点A作ADBC,交BC的延长线于点D.由题意,得SABC=12BCAD=126AD=12,解得AD=4.在RtABD中,BD=AB2-AD2=82-42=43, tanB=ADBD=443=33.5.D6.B解析 ABC中,ACBCAB=51213,设AC=5x,则BC=12x,AB=13x.(5x)2+(12x)2=(13x)2,ABC是直角三角形,C=90,cosA=ACAB=5x13x=513.故选B.7.解:如图,设为RtABC的一个锐角.cos=13,设BC=k,AB=3k.由勾股定理,得AC=AB2-BC2=(3k)2-k2=22k.sin=ACAB=2
6、23,tan=ACBC=22.8.解:在RtACD与RtABC中,ABC+CAD=90,ACD+CAD=90,ABC=ACD,在RtABC中,cosABC=cosACD=BCAB=45,令BC=4k,AB=5k,则AC=3k.由BEAB=35,知BE=3k,则CE=k,且CE=2,则k=2,AC=32,在RtACE中,tanAEC=ACCE=3,在RtACD中,CD=ACcosACD=125 2.9.B解析 连接BD.E,F分别是AB,AD的中点,BD=2EF=4.BC=5,CD=3,CD2+BD2=BC2,BCD是直角三角形,tanC=BDCD=43.10.B解析 如图,过点C作CDAB于点
7、D,过点A作AEBC于点E,设小正方形的边长为1.由勾股定理,得AB=AC=5,BC=2.由等腰三角形的性质,得BE=12BC=22.由勾股定理,得AE=AB2-BE2=322.由三角形的面积,得12ABCD=12BCAE,则CD=23225=355,sinCAB=CDAC=3555=35.故选B.11.解:ACB=90,CD是AB边上的中线,CD=12AB.设CD=x,则AB=2x,AC=32x,sinB=ACAB=34.12.43解析 过点A作AEBC于点E.AB=AC=5,BE=12BC=128=4,BAE=12BAC.BPC=12BAC,BPC=BAE.在RtBAE中,由勾股定理,得AE=AB2-BE2=3.tanBPC=tanBAE=BEAE=43.13.解:ACB=90,CDAB,ADC=ACB=90,A+ACD=90,BCD+ACD=90,BCD=A.AB=10,AC=8,cosBCD=cosA=ACAB=810=45.14.解:AB是O的直径,CDAB,ACB=90,AC=AD,ABD=ABC.BC=6,AC=8,根据勾股定理求得AB=10,sinABD=sinABC=810=45.
