1、2019-2020人教版广东省朝阳实验学校九年级数学上册第一次月考试卷一、选择题（每小题3分，共30分）1.关于x的一元二次方程x2-4x+m0的两实数根分别为x1、x2 ， 且x1+3x25，则m的值为（ ） A.74 B.75C.76D.0 2.若一次函数 y=kx+b 的图象不经过第二象限，则关于 x 的方程 x2+kx+b=0 的根的情况是（ ） A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定3.抛物线 y=x2+6x+7 可由抛物线 y=x2 如何平移得到的（ ） A.先向左平移3个单位，再向下平移2个单位B.先向左平移6个单位，再向上平移7个单位C.先向上平
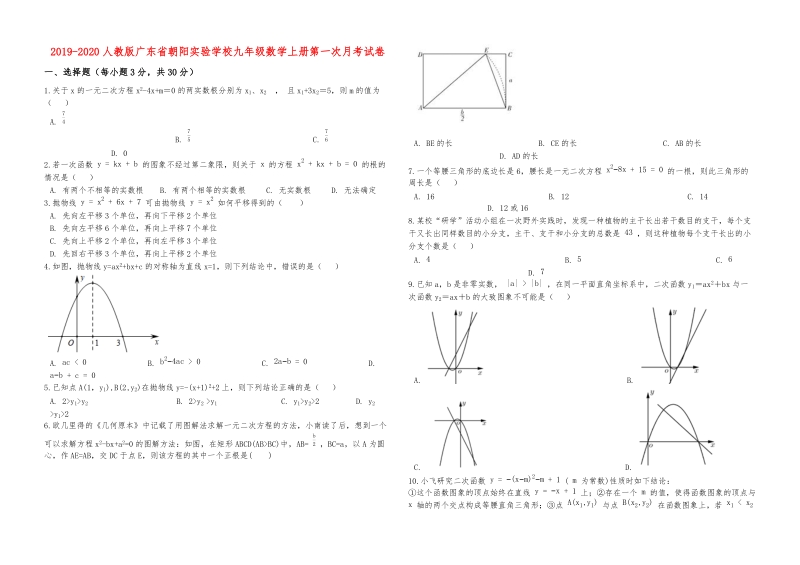
2、移2个单位，再向左平移3个单位D.先回右平移3个单位，再向上平移2个单位4.如图，抛物线y=ax2+bx+c的对称轴为直线x=1，则下列结论中，错误的是（ ） A.ac0C.2ab=0D.ab+c=05.已知点A(1，y1),B(2,y2)在抛物线y=-(x+1)2+2上，则下列结论正确的是（ ） A.2y1y2 B.2y2 y1 C.y1y22D.y2 y126.欧几里得的几何原本中记载了用图解法求解一元二次方程的方法，小南读了后，想到一个可以求解方程x2-bx+a2=0的图解方法：如图，在矩形ABCD(ABBC)中，AB= b2 ，BC=a，以A为圆心，作AE=AB，交DC于点E，则该方程
3、的其中一个正根是( ) A.BE的长B.CE的长C.AB的长D.AD的长7.一个等腰三角形的底边长是6，腰长是一元二次方程 x28x+15=0 的一根，则此三角形的周长是（ ） A.16B.12C.14D.12或168.某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是 43 ，则这种植物每个支干长出的小分支个数是（ ） A.4B.5C.6D.79.已知a，b是非零实数， |a|b| ，在同一平面直角坐标系中，二次函数y1ax2bx与一次函数y2axb的大致图象不可能是（ ） A.B.C.D.10.小飞研究二次
4、函数 y=(xm)2m+1 ( m 为常数)性质时如下结论： 这个函数图象的顶点始终在直线 y=x+1 上；存在一个 m 的值，使得函数图象的顶点与 x 轴的两个交点构成等腰直角三角形；点 A(x1,y1) 与点 B(x2,y2) 在函数图象上，若 x12m ，则 y1y2 ；当 1xb)abb2(ab) 例如4*2因为42，所以4*242428，若x1、x2是一元二次方程x29x200的两个根，则x1*x2_ 16.抛物线yax2+bx+c的顶点为D（1，2），与x轴的一个交点A在点（3，0）和（2，0）之间，其部分图象如图，则以下结论： b24ac0；当x1时y随x增大而减小；a+b+c0
5、；若方程ax2+bx+cm0没有实数根，则m2； 3a+c0其中，正确结论的序号是_ 三、解答题（每小题6分，共18分）17.解方程： （1）(x+1)23=0 （2）4(x+2)=3x(x+2) 18.关于x的一元二次方程x22mx+（m1）20有两个相等的实数根 （）求m的值；（II）求此方程的根19.抛物线yax2+2ax+c与x轴交于点A，B（点A在点B右边），且 AB=4 ，求点A、B的坐标 四解答题（每小题7分，共21分）20.关于x的一元二次方程（2m+1）x2+4mx+2m30（）当m 12 时，求方程的实数根；（）若方程有两个不相等的实数根，求实数m的取值范围；21.如图，一
6、农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m2？ 22.如图，二次函数y=(x+2)2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1，0)及点B（1）求二次函数与一次函数的表达式 （2）根据图象，写出满足(x+2)2kx+bm的x的取值范围 五。解答题（每小题9分，共27分） 23.某品牌手机去年每台的售价y（元）与月份x之间满足函数关系：y50x+2600，去年的
7、月销量p（万台）与月份x之间成一次函数关系，其中16月份的销售情况如下表： 月份（x）1月2月3月4月5月6月销售量（p）3.9万台4.0万台4.1万台4.2万台4.3万台4.4万台（1）求p关于x的函数关系式； （2）求该品牌手机在去年哪个月的销售金额最大？最大是多少万元？ （3）今年1月份该品牌手机的售价比去年12月份下降了m%，而销售量也比去年12月份下降了1.5m%今年2月份，经销商决定对该手机以1月份价格的“八折”销售，这样2月份的销售量比今年1月份增加了1.5万台若今年2月份这种品牌手机的销售额为6400万元，求m的值 24.暑假期间某景区商店推出销售纪念品活动，已知纪念品每件的进
8、货价为30元，经市场调研发现，当该纪念品的销售单价为40元时，每天可销售280件；当销售单价每增加1元，每天的销售数量将减少10件(销售利润=销售总额-进货成本) （1）若该纪念品的销售单价为45元时则当天销售量为_件。 （2）当该纪念品的销售单价为多少元时，该产品的当天销售利润是2610元。 （3）该纪念品的当天销售利润有可能达到3700元吗?若能，请求出此时的销售单价；若不能，请说明理由。 25.如图，已知抛物线yax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，5），对称轴为直线l，点M是线段AB的中点. （1）求抛物线的表达式； （2）写出点M的坐标并求直线AB的表达式； （
9、3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标. 2019-2020人教版广东省朝阳实验学校九年级数学上册第一次月考试卷一、选择题（30分）1.解： x 1 +x 2 4，则 x 1 +3x 2 5， 得 x 1 +x 2+2 x 2 5，2 x 2=5-4=1， x 2= 12, 代入原方程得： (12)2-412+m=0, m=74 故答案为A2.解： 一次函数 y=kx+b 的图象不经过第二象限， k0 ， b0 ，=k24b0 ， 方程有两个不相等的实数根。故答案为： A 。3.解：因为 y=x2+6x+7=(x+3)22
10、， 所以将抛物线 y=x2 先向左平移3个单位，再向下平移2个单位即可得到抛物线 y=x2+6x+7 。故答案为：A。4.解：A、由抛物线的开口向下知a0，与y轴的交点在y轴的正半轴上，可得c0，因此ac0，故不符合题意； B、由抛物线与x轴有两个交点，可得b2-4ac0，故不符合题意；C、由对称轴为x=- b2a =1，得2a=-b，即2a+b=0，故符合题意；D、由对称轴为x=1及抛物线过（3，0），可得抛物线与x轴的另外一个交点是（-1，0），所以a-b+c=0，故不符合题意。故答案为：C。5.解： y=-(x+1)2+2的顶点坐标为（-1,2），对称轴是直线x=-1，二次项系数a0，
11、当x=-1的时候函数有最大值y=2，当x-1的时候y随x的增大而减小， A(1，y1),B(2,y2) 21-1， 2y1y2 。 故答案为：A。 6.解：四边形ABCD是矩形，AD=BC=a, DE=AE2-AD2=b2-4a24=b2-4a22, CE=DC-DE=b-b2-4a22, x2-bx+a2=0， x=bb2-4ac2, 故答案为：B 7.解方程 x28x+15=0 ，得： x=3 或 x=5 ， 若腰长为3，则三角形的三边为3、3、6，显然不能构成三角形；若腰长为5，则三角形三边长为5、5、6，此时三角形的周长为16，故答案为：A 8.解：设这种植物每个支干长出 x 个小分支
12、， 依题意，得： 1+x+x2=43 ，解得： x1=7 （舍去）， x2=6 故答案为：C9.解：A.一次函数y2=ax+b图像过一、二、三象限, a0,b0，又二次函数y1=ax2+bx图像开口向上，a0,二次函数对称轴x=- b2a 0，b0，令y2=ax+b=0，解得：x=- ba|a|b|，-1- ba 0，故可能在同一直角坐标系中，A不符合题意；B.一次函数y2=ax+b图像过一、三、四象限,a0,b0，又二次函数y1=ax2+bx图像开口向上，a0,二次函数对称轴x=- b2a 0，b0，令y2=ax+b=0，解得：x=- ba|a|b|，0- ba 1，故可能在同一直角坐标系中
13、，B不符合题意；C.一次函数y2=ax+b图像过二、三、四象限,a0,b0，又二次函数y1=ax2+bx图像开口向下，a0,二次函数对称轴x=- b2a 0，b0，令y2=ax+b=0，解得：x=- ba|a|b|，-1- ba 0，故可能在同一直角坐标系中，C不符合题意；D.一次函数y2=ax+b图像过一、二、四象限,a0,b0，又二次函数y1=ax2+bx图像开口向下，a0,二次函数对称轴x=- b2a 0，b0，令y2=ax+b=0，解得：x=- ba|a|b|，0- ba 1，故不可能在同一直角坐标系中，D符合题意；故答案为：D.10.解：抛物线y=-（x-m）2-m+1 顶点坐标为：
14、（m，-m+1）y=-x+1当x=m时，y=-m+1抛物线的顶点坐标始终在直线y=-x+1上，故正确；设抛物线的顶点坐标C（m，-m+1），与x轴的两交点坐标为B、A过点C作CDx轴，当ACB是等腰直角三角形时，则AD=DB=CD=-m+1，OD=m点B的横坐标为：m+（-m+1）=1点B（1,0）-（1-m）2-m+1=0解之：m1=1（舍去），m2=0当m=0时，抛物线的顶点与x轴的两交点构成等腰直角三角形，故正确；A（x1 ， y1），B（x2 ， y2），x1+x22m x1+x22ma=-1，对称轴为直线x=m当xm时，y随x的增大而减小， x1y2 ，故错误；当-1x2时，y随x的
15、增大而增大，对称轴为直线x=mm2，故正确；故答案为：C二、填空题（24分）11. 解： 二次函数 y=x2+bx5 的对称轴为直线 x=2 b2=2 b=4 因此方程为 x24x5=2x13所以可得 x1=2,x2=4故答案为 x1=2 ， x2=4 .12.解：如图， 三块矩形区域的面积相等，矩形AEFD面积是矩形BCFE面积的2倍，AE2BE，设BCx，BEFCa，则AEHGDF2a，DF+FC+HG+AE+EB+EF+BC80，即8a+2x80，a 14 x+10，3a 34 x+30，矩形区域ABCD的面积S（ 34 x+30）x 34 x2+30x，a 14 x+100，x40，则
16、S 34 x2+30x（0x40）；S 34 x2+30x 34 （x20）2+300（0x40），且二次项系数为 34 0，当x20时，S有最大值，最大值为300m2。故答案为：300。 13.解：根据题意得： 44a（2c）0，整理得：4ac8a4，4a（c2）4，方程ax2+2x+2c0是一元二次方程，a0，等式两边同时除以4a得： c2=1a ，则 1a+c=2 ，故答案为：2.14.解： 设上面留白部分的宽度为xcm , 根据题意列方程得：（120+4x）（40+2x）=7000; 15.解： x29x200 （x-5）（x-4）=0 x-5=0或x-4=0 解之：x1=5，x2=4
17、或x2=5，x1=4 当x1=5，x2=4时，54 x1*x2=52-54=25-20=5 当x2=5，x1=4时，45 x1*x2=42-45=20-25=-5 故答案为：516.解：抛物线与x轴有两个交点， b24ac0，结论不正确抛物线的对称轴x1，当x1时，y随x增大而减小，结论正确抛物线与x轴的一个交点A在点（3，0）和（2，0）之间，抛物线与x轴的另一个交点在点（0，0）和（1，0）之间，当x1时，y0，a+b+c0，结论正确yax2+bx+c的最大值是2，方程ax2+bx+cm0没有实数根，则m2，结论正确抛物线的对称轴x b2a 1，b2a，a+b+c0，a+2a+c0，3a+
18、c0，结论正确综上，可得正确结论的序号是：故答案为：三、解答题（18分）17.（1）解：方程移项得： (x+1)2=3 ， 开方得： x+1=3 ，解得： x1=31 ， x2=31 ；（2）解：方程移项得： 4(x+2)3x(x+2)=0 ， 分解因式得： (x+2)(43x)=0 ，解得： x1=2 ， x2=43 18. （）方程x22mx+（m1）2=0有两个相等的实数根， =（2m）24（m1）2=8m4=0，解得：m= 12 ；（II）将m= 12 代入原方程，得：x2x+ 14 =0，即（x 12 ）2=0，解得：x1=x2= 12 19. 解：抛物线yax2+2ax+c， 抛物
19、线的对称轴为：直线x1，A在B右边，且AB4，B（3，0），A（1，0）四解答题（21分）20. 解：（）当m 12 时，方程为x2+x10，124（1）5，x 152 ，x1 1+52 ，x2 152 ；（）关于x的一元二次方程（2m+1）x2+4mx+2m30有两个不相等的实数根，0且2m+10，即（4m）24（2m+1）（2m3）0且m 12 ，m 34 且m 12 .21. 解：设矩形猪舍垂直于住房墙一边长为xm，可以得出平行于墙的一边的长为 (252x+1) m，由题意得 (252x+1)=80 化简，得 x213x+40=0 ，解得： x1=5,x2=8 当 x=5 时， 252x
20、+1=2525+1=1612 （舍去），当 x=8 时， 252x+1=2528+1=1012 ，答：所围矩形猪舍的长为10m、宽为8m。22. （1）解：把A点代入二次函数，解得m=1，二次函数表达式为y=(x+2)21B点坐标为(4，3)，从而一次函数为：y=x1（2）解：(x+2)2kx+bm把m移到左边的式子可得：(x+2)2+mkx+b，即二次函数大于一次函数，由图像可得，x的取值范围为：x1或者x4 五。解答题（27分） 23. （1）解：设pkx+b， 把p=3.9，x=1；p=4.0，x=2分别代入p=kx+b中，得： k+b=3.92k+b=4.0, 解得： k=0.1b=3
21、.8 ，p=0.1x+3.8（2）解：设该品牌手机在去年第x个月的销售金额为w万元， w（50x+2600）（0.1x+3.8）5x2+70x+98805（x7）2+10125，当x7时，w最大10125，答：该品牌手机在去年七月份的销售金额最大，最大为10125万元；（3）解：当x12时，y2000，p5， 1月份的售价为：2000（1m%）元，则2月份的售价为：0.82000（1m%）元；1月份的销量为：5（11.5m%）万台，则2月份的销量为：5（11.5m%）+1.5万台；0.82000（1m%）5（11.5m%）+1.56400，解得：m1% 53 （舍去），m2% 15 ，m=20
22、，答：m的值为2024. （1）230（2）解： 设销售价定为x元，销售利润是2610元，280-（x-40）10（x-30）=2610,-10(x-49)2+3610=2610，(x-49)2=100，x-49=10, 或x-49=-10,x=59或x=39, 该纪念品的销售单价为59元或39元时，该产品的当天销售利润是2610元。 （3）解： 设销售价为x, 销售利润为y, 则：y=280-（x-40）10（x-30）=-10x2+980x-20400=-10(x-49)2+3610a=-100, 当x=49时，y最大=36103700,销售利润不可能达到3700元. 25. （1）解：
23、函数表达式为：ya（x-4）2+3，将点B坐标代入上式并解得：a 12 ，故抛物线的表达式为：y 12 x2+4x5；（2）解：A（4，3）、B（0，5），则点M（2，1）， 设直线AB的表达式为：ykx5，将点A坐标代入上式得：34k5，解得：k2，故直线AB的表达式为：y2x5（3）解：设点Q（4，s）、点P（m， 12 m2+4m5）， 当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，同样点P（m， 12 m2+4m5）向左平移2个单位、向下平移4个单位得到Q（4，s），即：m24， 12 m2+4m54s，解得：m6，s3，故点P、Q的坐标分别为（6，1）、（4，3）；当AM是平行四边形的对角线时，由中点定理得：4+2m+4，31 12 m2+4m5+s，解得：m2，s1，故点P、Q的坐标分别为（2，1）、（4，1）；当点Q在点A上方时，AQMP2，同理可得点Q的坐标为（4，5），故点P、Q的坐标分别为（6，1）或（2，1）、（4，3）或（4，1）或（4，5）
