1、2018 年北京市民大附中高考数学三模试卷（文科）一、选择题共 8 小题，每小题 5 分，共 40 分。在每小题列出的四个选项中，选出符合题目要求的一项。1 （5 分）已知集合 Ax|2x4，Bx|x3 或 x5，则 AB（ ）A x|2x5 Bx|x4 或 x5 C x|2x3 D x|x2 或 x52 （5 分）阅读右面的程序框图，运行相应的程序，若输入 N 的值为 24，则输出 N 的值为（ ）A0 B1 C2 D33 （5 分）已知 z1，z 2 是两个复数，则“z 1z 2”是“|z 1|z 2|”的（ ）A充分而不必要条件 B必要而不充分条件C充
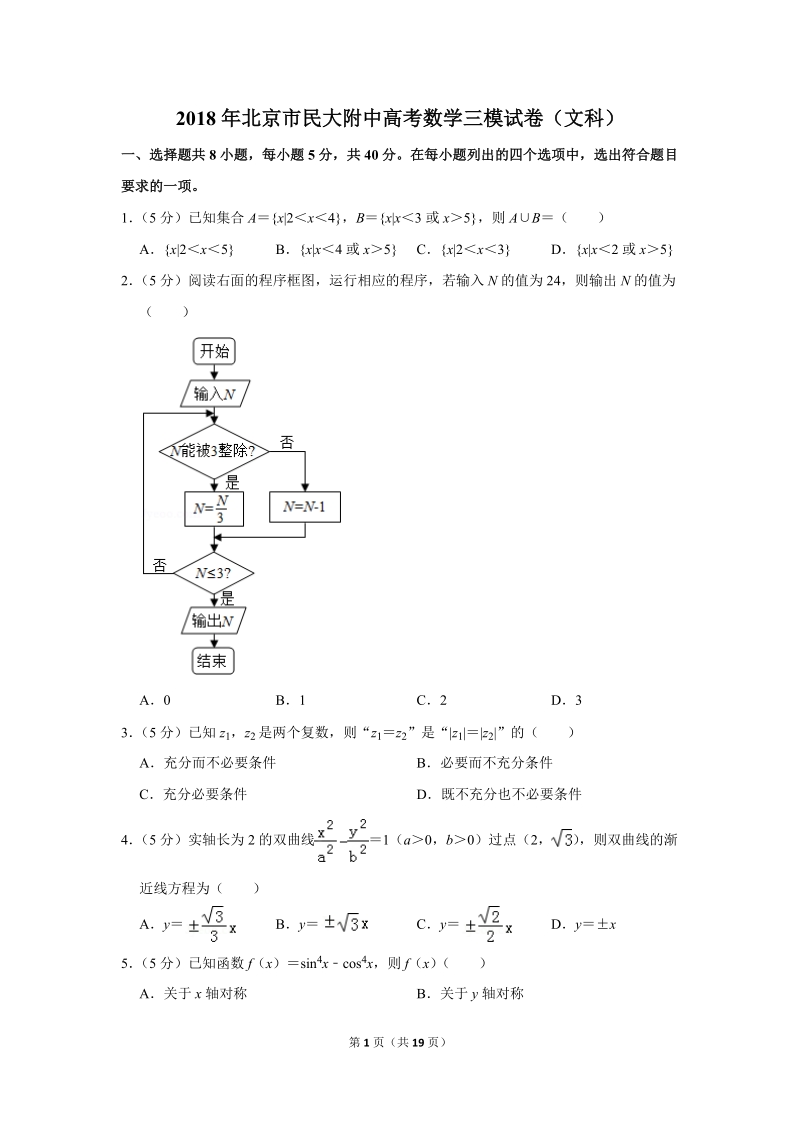
2、分必要条件 D既不充分也不必要条件4 （5 分）实轴长为 2 的双曲线 1（a0，b0）过点（2， ） ，则双曲线的渐近线方程为（ ）Ay By Cy Dy x5 （5 分）已知函数 f（x ）sin 4xcos 4x，则 f（x） （ ）A关于 x 轴对称 B关于 y 轴对称第 2 页（共 19 页）C关于原点对称 D关于 x 对称6 （5 分）一个几何体的三视图如图所示，则这个几何体的体积为（ ）A B C8 D7 （5 分）设函数 f（x ） （a R） ，当 f（x）在（0，+）上为单调函数时，a 的取值范围为 M；当存在 b 使得函数 yf（x）b
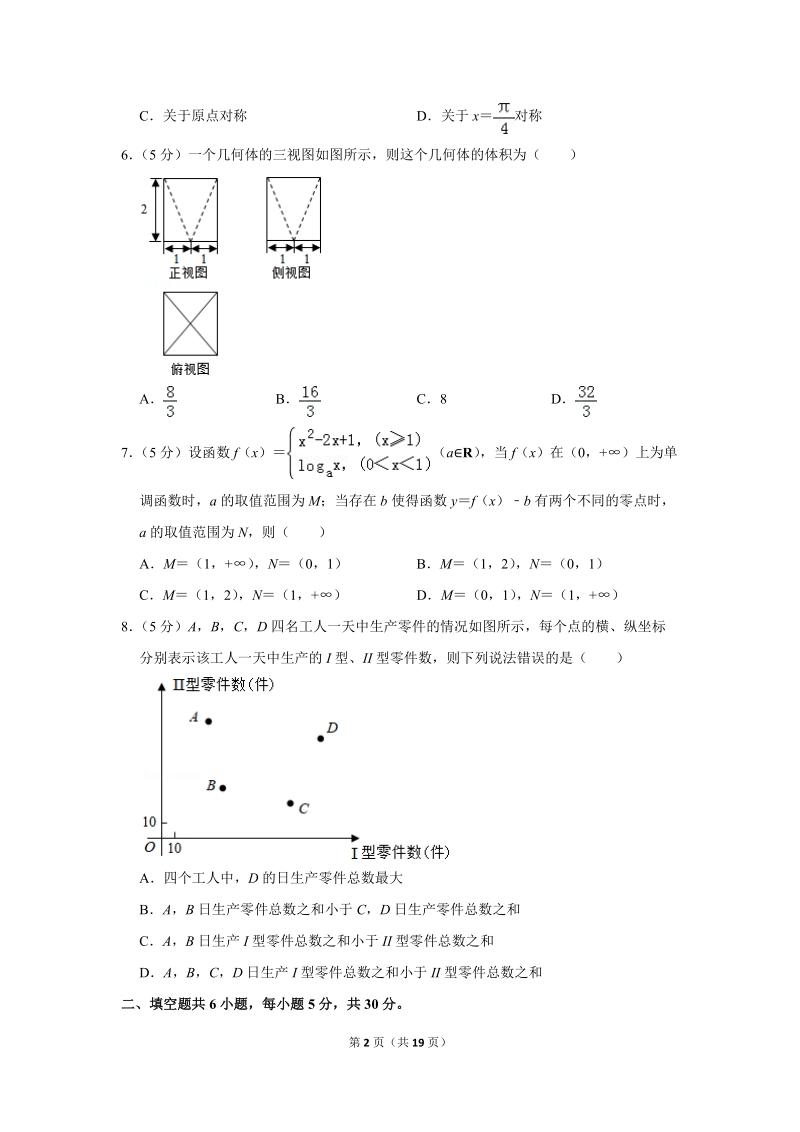
3、 有两个不同的零点时，a 的取值范围为 N，则（ ）AM（1，+） ，N（0，1） BM （1，2） ，N（0，1）CM（1，2） ，N（1，+） DM（0，1） ，N （1，+）8 （5 分）A，B，C，D 四名工人一天中生产零件的情况如图所示，每个点的横、纵坐标分别表示该工人一天中生产的 I 型、II 型零件数，则下列说法错误的是（ ）A四个工人中，D 的日生产零件总数最大BA，B 日生产零件总数之和小于 C，D 日生产零件总数之和CA，B 日生产 I 型零件总数之和小于 II 型零件总数之和DA，B ，C ，D 日生产 I 型零件总数之和小于 II 型零件总数之
4、和二、填空题共 6 小题，每小题 5 分，共 30 分。第 3 页（共 19 页）9 （5 分）在ABC 中，若 b1，c ，则 a 10 （5 分）已知 A（1，3） ，B（3，1） ，C （2，1） ，记ABC 及其内部的点组成的集合为D，P（ x，y ）为 D 中任意一点，则 的取值范围是 11 （5 分）举例说明命题“若 f（x ） ，g（x）在定义域内均为增函数，则 f（x）g（x）是增函数”是假命题，例如：f（x ） ，g（x） 12 （5 分）在一个容量为
5、5 的样本中，数据均为整数，已测出其平均数为 10，但墨水污损了两个数据，其中一个数据的十位数字 1 未污损，即 9，10，11，1 ，那么这组数据的方差最大的时候被污损了两个数据分别是 和 13 （5 分）已知抛物线 x24y 的准线与圆心为 C（0，1）半径为 3 的圆交于 A，B 两点，那么| | 14 （5 分）四个足球队进行单循环比赛（每两队比赛一场） ，每场比赛胜者得 3 分，负者得 0 分，平局双方各得 1 分比赛结束后发现没有足球队全胜，且四队得分各不相同，则所有比赛中可
6、能出现的最少平局场数是 三、解答题共 6 小题，共 80 分。解答应写出文字说明、演算步骤或证明过程。15 （13 分）已知函数 f（x ）2cos 2xcos （2x+ ） （）求 f（ ）及 f（x）的最小正周期；（）求 f（x）在 上的值域16 （13 分）已知数列a n中，a 19，a na n+12（）求数列a n的通项公式（）记 bna n+an+1，数列 bn的前 n 项和为 Sn，求当 Sn 取得最小值时 n 的取值17 （13 分）民大附中的甲、乙两人同时参加某大学的自主招生，在申请材料中提交了某学科 10 次的考试成绩（满分 100） ，记录如下
7、：甲：78，86，95，97，88，82，76，89，92，95乙：73，83，69，82，93，86，79，75，84，99（）根据两组数据完成两人成绩的茎叶图，并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系（不要求计算具体值，直接写出结论即可）：（）现将两人名次分为三个等级：成绩分数 0，70） 70，90） 90，100）第 4 页（共 19 页）等级 合格 良好 优秀根据所给数据，从甲、乙获得“优秀”的成绩中各随机选取一个，求甲同学成绩高于乙同学成绩的概率；18 （14 分）如图，在P 1CD 中D 为直角，ABCD，CD2AB，将P 1AB 沿着 AB 折到PAB 的
8、位置，使得平面 PAB底面 ABCD，E 是 CD 中点（）求证：PA底面 ABCD；（）求证：BE平面 PAD；（）在线段 PC 上是否存在一点 F 使得平面 BEF平面 PCD？若存在，求出 的值，若不存在，说明理由19 （13 分）已知椭圆 C： 1（ab0）过点（2 ，0） ，且焦距为 4，O 为原点（1）求椭圆 C 的方程及离心率；（）设 A，B 为短轴端点（点 A 位于点 B 的上方） ，直线 ykx +4 与曲线 C 交于不同的两点 P，Q，直线 y1 与直线 BP 交于点 D求证：A，D，Q 三点在一条直线上20 （14 分）已知函数 f（x ）ax 2+axxe x，a1（）
9、若曲线 f（x ）在点（0，f（0） ）处的切线方程为 yx，求 a 的值；（）当 a1 时，求 f（x ）的零点；（）证明：当 x0 时，函数 f（x）存在唯一的极小值点为 x0，且 x 00第 5 页（共 19 页）2018 年北京市民大附中高考数学三模试卷（文科）参考答案与试题解析一、选择题共 8 小题，每小题 5 分，共 40 分。在每小题列出的四个选项中，选出符合题目要求的一项。1 （5 分）已知集合 Ax|2x4，Bx|x3 或 x5，则 AB（ ）A x|2x5 Bx|x4 或 x5 C x|2x3 D x|x2 或 x5【分析】由题意结合所给的集合 A，B 的表示形
10、式和并集的定义进行并集运算即可求得最终结果【解答】解：由题中所给的集合结合并集的定义可得：ABx|x4 或 x5 故选：B【点评】本题考查集合的表示方法，并集运算等，重点考查学生对基础概念的理解和计算能力，属于基础题2 （5 分）阅读右面的程序框图，运行相应的程序，若输入 N 的值为 24，则输出 N 的值为（ ）A0 B1 C2 D3【分析】根据程序框图，进行模拟计算即可【解答】解：第一次 N24，能被 3 整除，N 3 不成立，第二次 N8，8 不能被 3 整除， N817，N73 不成立，第 6 页（共 19 页）第三次 N7，不能被 3 整除， N716，N 23 成立，输
11、出 N2，故选：C【点评】本题主要考查程序框图的识别和应用，根据条件进行模拟计算是解决本题的关键3 （5 分）已知 z1，z 2 是两个复数，则“z 1z 2”是“|z 1|z 2|”的（ ）A充分而不必要条件 B必要而不充分条件C充分必要条件 D既不充分也不必要条件【分析】由“z 1z 2”“|z1|z 2|”，反之不成立即可判断出结论【解答】解：“z 1z 2”“|z1|z 2|”，反之不成立，例如取 z1i，z 2iz 1，z 2 是两个复数，则“z 1z 2”是“|z 1| z2|”的充分不必要条件故选：A【点评】本题考查了复数的性质、充要条件的判定方法，考查了推理能力与计
12、算能力，属于基础题4 （5 分）实轴长为 2 的双曲线 1（a0，b0）过点（2， ） ，则双曲线的渐近线方程为（ ）Ay By Cy Dy x【分析】利用双曲线的实轴长以及经过的点，求出 b，然后求解双曲线的渐近线方程【解答】解：双曲线 1（a0，b0）实轴长为 2，且经过点（2， ） ，可得 ，解得 b1则双曲线的渐近线方程为：yx故选：D【点评】本题考查双曲线的简单性质的应用，考查计算能力5 （5 分）已知函数 f（x ）sin 4xcos 4x，则 f（x） （ ）A关于 x 轴对称 B关于 y 轴对称C关于原点对称 D关于 x 对称第 7 页（共 19 页）【
13、分析】利用二倍角公式化简函数的解析式，再根据三角函数的图象的对称性，得出结论【解答】解：函数 f（x ）sin 4xcos 4x（sin 2xcos 2x ）（sin 2x+cos2x ）cos2x，故 f（x）为偶函数，故它的图象关于 y 轴对称，故选：B【点评】本题主要考查二倍角公式，三角函数的图象的对称性，属于基础题6 （5 分）一个几何体的三视图如图所示，则这个几何体的体积为（ ）A B C8 D【分析】几何体是正方体挖去一个同底等高的倒正四棱锥，根据三视图的数据代入体积公式计算【解答】解：由三视图知：几何体是正方体挖去一个同底等高的倒正四棱锥，正方体的棱长为 2，几何体的
14、体积 V2 3 222 故选：B【点评】本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是关键7 （5 分）设函数 f（x ） （a R） ，当 f（x）在（0，+）上为单调函数时，a 的取值范围为 M；当存在 b 使得函数 yf（x）b 有两个不同的零点时，a 的取值范围为 N，则（ ）AM（1，+） ，N（0，1） BM （1，2） ，N（0，1）第 8 页（共 19 页）CM（1，2） ，N（1，+） DM（0，1） ，N （1，+）【分析】当 f（x ）在（0，+）上为单调函数，由 x1 时，f（x）递增，可得 f（x ）在x0 上递增，可得
15、 a1；由存在 b 使得函数 yf （x）b 有两个不同的零点时，即f（x）b 有两个不等实根，可得 0a1，可得所求答案【解答】解：函数 f（x ） （aR） ，当 f（x）在（0 ，+）上为单调函数，由 x1 时，f（ x）递增，可得 f（x ）在 x0 上递增，即有 a1，即 a 的范围是 M（1，+ ） ；由存在 b 使得函数 yf（x）b 有两个不同的零点时，即 f（x）b 有两个不等实根，可得 0a1，即 N（0，1） 故选：A【点评】本题考查函数方程的转化思想，注意对数函数的单调性，考查数形结合思想方法，属于基础题8 （5 分）A，B，C，D 四名工人一天中生产零件的情况如图所示
16、，每个点的横、纵坐标分别表示该工人一天中生产的 I 型、II 型零件数，则下列说法错误的是（ ）第 9 页（共 19 页）A四个工人中，D 的日生产零件总数最大BA，B 日生产零件总数之和小于 C，D 日生产零件总数之和CA，B 日生产 I 型零件总数之和小于 II 型零件总数之和DA，B ，C ，D 日生产 I 型零件总数之和小于 II 型零件总数之和【分析】结合图形得到：A，B，C ，D 日生产 I 型零件总数之和大于 II 型零件总数之和【解答】解：由图形得：在 A 中，四个工人中，D 的日生产零件总数最大， B 生产零件总数最小，故 A 正确；在 B 中，A ，B 日生产
17、零件总数之和小于 C，D 日生产零件总数之和，故 B 正确；在 C 中，A，B 日生产 I 型零件总数之和小于 II 型零件总数之和，故 C 正确；在 D 中，A，B，C，D 日生产 I 型零件总数之和大于 II 型零件总数之和，故 D 错误故选：D【点评】本题考查命题真假的判断，考查图形的性质等基础知识，考查运算求解能力、数据处理能力，考查函数与方程思想、数形结合思想，是基础题二、填空题共 6 小题，每小题 5 分，共 30 分。9 （5 分）在ABC 中，若 b1，c ，则 a 2 【分析】根据余弦定理 a2c 2+b22cbcosA 的式子，结合题中数据加以计算，即可得到边 a 的值【解
18、答】解：根据余弦定理 a2c 2+b22cbcosA，可得a2（ ） 2+122 cos 4a2（舍负）故答案为：2【点评】本题给出三角形的两边及其夹角大小，求第三边长着重考查了利用余弦定理第 10 页（共 19 页）解三角形的知识，属于基础题10 （5 分）已知 A（1，3） ，B（3，1） ，C （2，1） ，记ABC 及其内部的点组成的集合为D，P（ x，y ）为 D 中任意一点，则 的取值范围是 【分析】根据 A、B、C 的坐标画出如图可行域，得到如图所示的ABC 及其内部的区域设 P（x， y） 、O（0，0） ，可得 k 表示直线 P、O 连线的斜率，运动点 P 得到PO 斜率的最
19、大、最小值，即可得到 的取值范围【解答】解：根据 A、B、C 的坐标作出图形，得到如图所示的ABC 及其内部的区域设 P（x ，y）为区域内的动点，可得O（0，0） ，则 k 表示直线 P、O 连线的斜率，运动点 P，可得：当 P 与 B 点重合时，k BO 达到最小值；当 P 与 A 点重合时，k AO3 取得最大值，k 的取值范围是 ，3故答案为： ，3【点评】本题给出二元一次不等式组，求 的取值范围着重考查了直线的斜率公式、二元一次不等式组表示的平面区域和简单的线性规划等知识，属于中档题11 （5 分）举例说明命题“若 f（x ） ，g（x）在定义域内均为增函数，则 f（x）g（x）是增
20、函数”是假命题，例如：f（x ） x 3 ，g（x） x 第 11 页（共 19 页）【分析】根据题意，依据函数的单调性的性质，举出反例即可得答案【解答】解：根据题意，设 f（x ）x 3g（x）x，两个函数的定义域为 R，则 f（x）g（x）x 4，f（x）g（x）不是增函数；满足题意故答案为：x 3，x （答案不唯一） 【点评】本题考查函数单调性的判定以及性质，关键是掌握函数单调性的性质12 （5 分）在一个容量为 5 的样本中，数据均为整数，已测出其平均数为 10，但墨水污损了两个数据，其中一个数据的十位数字 1 未污损，即 9，10，11，1 ，那么这组数据的方差最大的时候
21、被污损了两个数据分别是 19 和 1 【分析】设这组数据的最后 2 个分别是：10+x，y，得到 x+y10，表示出 S2，根据 x 的取值求出 S2 的最大值即可求出这组数据的方差最大的时候被污损了两个数据【解答】解：设这组数据的最后 2 个分别是：10+x，y，则 9+10+11+（10+x）+y50，得：x+y10，故 y10x，故 S2 1+0+1+x2+（x ） 2 + x2，当 x 最大取 9 时，S 2 最大是 ，这组数据的方差最大的时候被污损了两个数据分别是 19，1故答案为：19，1【点评】本题考查这组数据的方差最大的时候被污损了两个数据的求法，考查方差的性质等基
22、础知识，考查运算求解能力，是基础题13 （5 分）已知抛物线 x24y 的准线与圆心为 C（0，1）半径为 3 的圆交于 A，B 两点，那么| | 4 【分析】求出圆的方程，然后抛物线的准线方程代入圆的方程，求出 AB 坐标，然后求解向量的模【解答】解：圆心为 C（0， 1）半径为 3 的圆方程 x2+（ y1） 29，抛物线 x24y 的准线为 x 1，代入到圆的方程可得 ， ，A（1，12 ） ，B（1，1+2 ） ， ， （1，2 ） ， （0，4 ） ，第 12 页（共 19 页）| |4 ，故答案为：4 【点评】本题考查抛物线的简单性质圆的方程的应用，考查转
23、化思想以及计算能力14 （5 分）四个足球队进行单循环比赛（每两队比赛一场） ，每场比赛胜者得 3 分，负者得 0 分，平局双方各得 1 分比赛结束后发现没有足球队全胜，且四队得分各不相同，则所有比赛中可能出现的最少平局场数是 1 【分析】四支足球队进行单循环比赛（每两队比赛一场） ，共比赛 6 场；根据比赛规则知每场比赛若不平局，则共产生 3618 分，每场比赛都平局，则共产生 2612 分；根据比赛结果知各队得分情况，经过分析可得正确的结论【解答】解：四支足球队进行单循环比赛（每两队比赛一场） ，共比赛 6 场；每场比赛胜者得 3 分，负者得 0 分，平局双方各得 1 分；即每场比赛若不平
24、局，则共产生 3618 分，每场比赛都平局，则共产生 2612 分；比赛结束后发现没有足球队全胜，且四队得分各不相同，则各队得分分别为：2，3，4，5；或 3，4，5，6如果是 3，4，5，6，则每场产生 3 分，没有平局产生，但是不可能产生 4，5 分，与题意矛盾，舍去；因此各队得分分别为：2，3，4，5第一名得分 5：53+1+1，为一胜两平；第二名得分 4：43+1+0，为一胜一平一负；第三名得分 3：根据胜场等于负场，只能为三平；第四名得分 2：21+1+0，为两平一负则所有比赛中可能出现的最少平局场数是 1故答案为：1【点评】本题考查了单循环比赛问题，也考查了分析问题、解决问题的能力
25、，其中各队得分各不相同是解题的关键三、解答题共 6 小题，共 80 分。解答应写出文字说明、演算步骤或证明过程。15 （13 分）已知函数 f（x ）2cos 2xcos （2x+ ） 第 13 页（共 19 页）（）求 f（ ）及 f（x）的最小正周期；（）求 f（x）在 上的值域【分析】 （）利用二倍角，诱导公式和辅助角公式化简，即可求 f（ ）及 f（x ）的最小正周期；（）由 x 在 上，求解内层函数的范围，即可求解值域；【解答】解：（）函数 f（ x）2cos 2xcos （2x+ ）1+cos2x+sin2 x sin（2x+）+1，当 x 时，即 f（ ） sin（2 + ）+1
26、2f（x）的最小正周期 T（）由 x 在 上，2x+ ， ，则 sin（2x+ ）1， f（x）在 上的值域为 ，2 【点评】本题考查三角函数的化简和图象性质的应用，考查转化思想以及计算能力16 （13 分）已知数列a n中，a 19，a na n+12（）求数列a n的通项公式（）记 bna n+an+1，数列 bn的前 n 项和为 Sn，求当 Sn 取得最小值时 n 的取值【分析】 （）直接利用已知条件建立等量关系，求出数列的通项公式（）利用（）的结论，首项求出 bn 的通项公式，进一步利用前 n 项和公式，再利用二次函数的性质求出结果【解答】解：（）数列a n中，a 19，a na n+
27、12则：a n+1a n2（常数） ，数列a n是以 a19 为首项，2 为公差的等差数列故：a n9+2（n1）2n11（）由于（）a n2n11，第 14 页（共 19 页）则：a n+12n9，所以 bna n+an+12n11+2n94n20，故： 2n 218n ，当 n4 或 5 时 Sn 取得最小值【点评】本题考查的知识要点：数列的通项公式的求法及应用，数列的前 n 项和公式的应用，主要考查学生的运算能力和转化能力，属于基础题型17 （13 分）民大附中的甲、乙两人同时参加某大学的自主招生，在申请材料中提交了某学科 10 次的考试成绩（满分 100） ，记录如下：甲：78，86，
28、95，97，88，82，76，89，92，95乙：73，83，69，82，93，86，79，75，84，99（）根据两组数据完成两人成绩的茎叶图，并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系（不要求计算具体值，直接写出结论即可）：（）现将两人名次分为三个等级：成绩分数 0，70） 70，90） 90，100）等级 合格 良好 优秀根据所给数据，从甲、乙获得“优秀”的成绩中各随机选取一个，求甲同学成绩高于乙同学成绩的概率；【分析】 （）由题意画出茎叶图，根据茎叶图中的数据得出二者的平均值和方差的大小；（）由表中数据知甲、乙优秀的数据，用列举法求得基本事件数，计算所求的概率值【解
29、答】解：（）画出甲、乙成绩的茎叶图如下；通过茎叶图可以看出，甲成绩的平均值高于乙成绩的平均值，甲的成绩分布比较集中，乙的成绩分布相对分散，故甲成绩的方差小于乙成绩的方差；（）由表中数据知，甲优秀的数据为 95，97，92，95；乙优秀的数据为 93，99；从这两组数据中各随机选取一个，基本事件是（95，93） ， （95，99） ， （97，93） ， （97，99） ，（92，93） ， （92，99） ， （95，93） ， （95，99）共 8 种不同取法；第 15 页（共 19 页）甲同学成绩高于乙同学成绩的是（95，93） ， （97，93） ， （95，93）共 3 种不同取法；故
30、所求的概率为 P 【点评】本题考查了茎叶图与平均数、方差和列举法求古典概型的根据计算问题，是基础题18 （14 分）如图，在P 1CD 中D 为直角，ABCD，CD2AB，将P 1AB 沿着 AB 折到PAB 的位置，使得平面 PAB底面 ABCD，E 是 CD 中点（）求证：PA底面 ABCD；（）求证：BE平面 PAD；（）在线段 PC 上是否存在一点 F 使得平面 BEF平面 PCD？若存在，求出 的值，若不存在，说明理由【分析】 （）由题意，利用面面垂直的性质定理，即可证明 PA底面 ABCD；（）利用线面平行的判定定理，即可证明 BE平面 PAD；（）在线段 PC 上存在一点 F，使
31、得平面 BEF平面 PCD，且 ；点 F 是 PC的中点，由此证明平面 BEF平面 PCD【解答】解：（）证明：由D 为直角，ABCD，ABPA，又平面 PAB底面 ABCD，且平面 PAB平面 ABCDAB，PA底面 ABCD；（）证明：由 ABCD，CD2AB，第 16 页（共 19 页）B 是 P1C 的中点，又 E 是 CD 中点，BEAD ，又 BE平面 PAD，AD 平面 PAD，BE平面 PAD；（）在线段 PC 上存在一点 F，使得平面 BEF平面 PCD，此时 ；理由如下：CDAD，BE AD，CDBE ，又 PA平面 ABCD，CD 平面 ABCD，PACD，且 PAAD
32、A，CD平面 PAD；取 PC 的中点 F，由 E 为 CD 的中点，FEPD ，又 PDAD D ，BEFEE，平面 BEF平面 PAD，CD平面 BEF；又 CD平面 PCD，平面 BEF平面 PCD，且 【点评】本题考查了线面平行、线面垂直以及面面平行和垂直的应用问题，是中档题19 （13 分）已知椭圆 C： 1（ab0）过点（2 ，0） ，且焦距为 4，O 为原点（1）求椭圆 C 的方程及离心率；（）设 A，B 为短轴端点（点 A 位于点 B 的上方） ，直线 ykx +4 与曲线 C 交于不同的两点 P，Q，直线 y1 与直线 BP 交于点 D求证：A，D，Q 三点在一条直线上【分析
33、】 （）由条件可得 c2，a2 ，由 a，b，c 的关系可得 b，即可得到所求椭第 17 页（共 19 页）圆方程和离心率；（）由已知直线代入椭圆方程化简得：（2k 2+1）x 2+16kx+240，32（2k 23）0，解得 k 的范围，设 Q（x 2，kx 2+4） ，P（x 1，kx 1+4） ，D （x 0，1） ，以及直线 BP 的方程，令 y1 可得 D 的坐标，运用三点共线的条件：斜率相等，结合韦达定理，即可得证【解答】解：（）椭圆 C： 1（ab0）过点（2 ，0） ，且焦距为 4，可得 2c4，即 c2，且 a2 ，即有 b 2，则椭圆方程为 + 1，e ；（）证明：由椭圆方
34、程可得 A（0，2） ，B（0，2） ，由直线 ykx+4 代入椭圆方程 x2+2y28，化简得（2k 2+1）x 2+16kx+240，设 P（x 1，y 1） ，Q（x 2，y 2） ，32（2k 23）0，解得：k 或 k ，由韦达定理得：x 1+x2 ，x 1x2 ，设 Q（x 2，kx 2+4） ，P（x 1，kx 1+4） ，D （x 0，1） ，PB 方程为：y x2 ，则 D（ ，1） ，由 kAD ，k AQ ，由 kAQ kAD + + 0，即 kAQ kAD，可得三点 A，D，Q 共线第 18 页（共 19 页）【点评】本题考查椭圆的标准方程和性质，考查直线与椭圆的位置关
35、系，解题的关键是直线与椭圆方程联立，利用韦达定理进行求解，考查三点共线，注意运用斜率相等，考查运算能力，属于中档题20 （14 分）已知函数 f（x ）ax 2+axxe x，a1（）若曲线 f（x ）在点（0，f（0） ）处的切线方程为 yx，求 a 的值；（）当 a1 时，求 f（x ）的零点；（）证明：当 x0 时，函数 f（x）存在唯一的极小值点为 x0，且 x 00【分析】 （I）f（x ）2ax +ae xxe x，a1根据曲线 f（x）在点（0，f（0） ）处的切线方程为 yx ，可得 f（0）a11，解得 a（II）a1 时，f （x ）x 2+xxe x，f （0）0f（x
36、） 2x+1e xxe x，f （x）2（1e x）xe x，利用导数研究其单调性即可证明结论（III）f（x）2ax +ae xxe x，a1，x0f （x ）2（ae x）xe x0，可得函数 f（x）在（ ，0）上单调递增，根据函数零点判定定理即可判断出结论f（x）在 内存在唯一零点即可证明结论【解答】 （I）解：f（x ）2ax +ae xxe x，a1曲线 f（x）在点（ 0，f（0） ）处的切线方程为 yx ，f（0）a11，解得 a2（II）解：a1 时，f （x ）x 2+xxe x，则 f（0）0f（x）2x+1e xxe x，f （x）2（1 e x）xe x，可得：x0 时，f （x）0；x0 时，f （x）0；x0 时，f （0）0x0 时，函数 f（x）取得极小值，因此函数 f（x ）f（0）0函数 f（x）在 R 上单调递增，存在唯一零点 0（III）证明： f（x）2ax +ae xxe x，a1，x0f （x）2（a e x）xe x0，函数 f（x）在（ ，0）上单调递增，第 19 页（共 19 页）又 f（0）a10， 0f（x）在 内存在唯一零点因此当 x0 时，函数 f（x）存在唯一的极小值点为 x0，且 x 00【点评】本题考查了利用导数研究函数的单调性及其切线方程、方程与不等式的解法，考查了推理能力与计算能力，属于难题
