1、人教版 2019-2020 学年八年级（上）期末数学模拟试卷一、选择题（每小题 3 分，共 30 分）1（3 分）用直角三角板，作ABC 的高，下列作法正确的是（ ）A BC D2（3 分）七巧板是一种传统智力游戏，是中国古代劳动人民的发明，用七块板可拼出许多有趣的图形在下面这些用七巧板拼成的图形中，可以看作轴对称图形的（不考虑拼接线）有（ ）A5 个 B4 个 C3 个 D2 个3（3 分）化简分式 的结果是（ ）A B C D4（3 分）世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为 0.056 盎司将 0.056 用科学记数法表示为（ ）A5.610 1 B5.610 2 C5.61
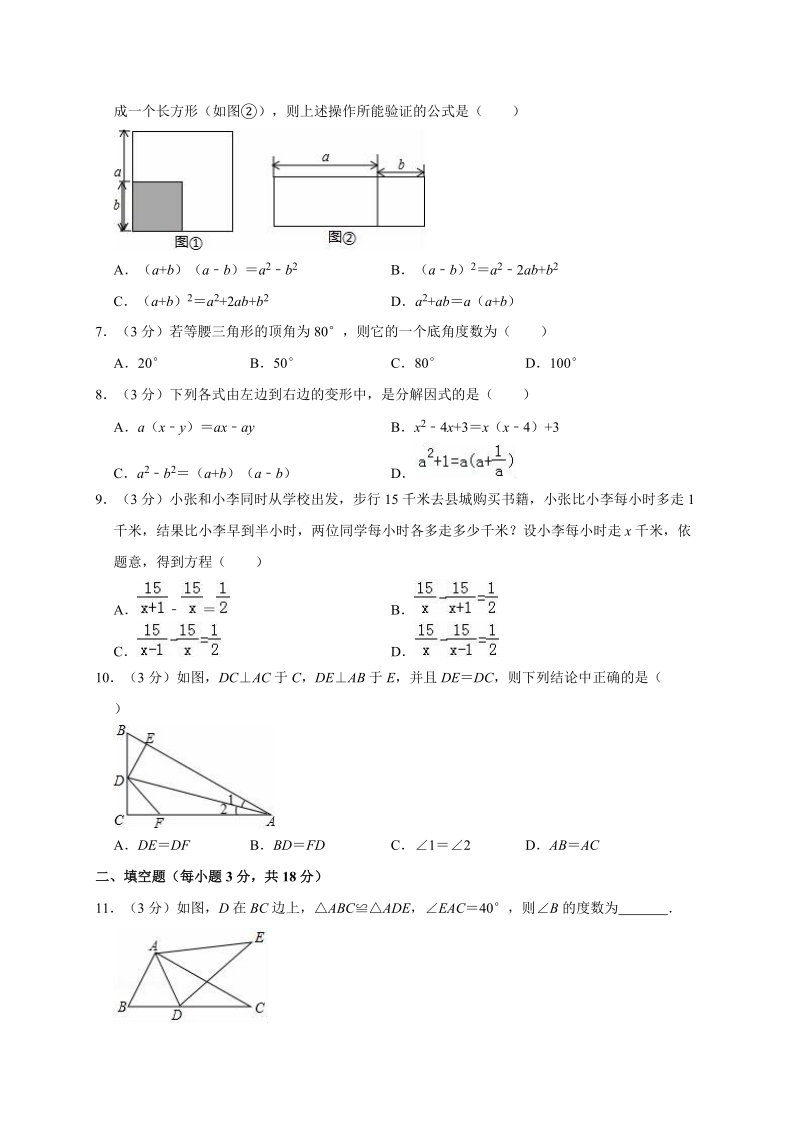
2、0 3 D0.5610 15（3 分）下列运算正确的是（ ）Ab 5b3b 2 B（b 5） 2b 7Cb 2b4b 8 Da（a 2b）a 2+2ab6（3 分）如图，从边长为 a 的正方形中剪去一个边长为 b 的小正方形，然后将剩余部分剪拼成一个长方形（如图），则上述操作所能验证的公式是（ ）A（a+b）（ ab）a 2b 2 B（ab） 2a 22ab+b 2C（a+b） 2a 2+2ab+b2 Da 2+ab a（a+b）7（3 分）若等腰三角形的顶角为 80，则它的一个底角度数为（ ）A20 B50 C80 D1008（3 分）下列各式由左边到右边的变形中，是分解因式的是（ ）Aa（
3、xy）axay Bx 24x+3x（x4）+3Ca 2b 2（a+ b）（ab） D9（3 分）小张和小李同时从学校出发，步行 15 千米去县城购买书籍，小张比小李每小时多走 1千米，结果比小李早到半小时，两位同学每小时各多走多少千米？设小李每小时走 x 千米，依题意，得到方程（ ）A BC D10（3 分）如图，DCAC 于 C，DE AB 于 E，并且 DEDC，则下列结论中正确的是（ ）ADEDF BBD FD C12 DAB AC二、填空题（每小题 3 分，共 18 分）11（3 分）如图，D 在 BC 边上，ABCADE，EAC40，则B 的度数为 12（3 分）分解因式：3x 26
4、x+3 13（3 分）如图，将ABC 绕点 A 逆时针旋转至ADE 处，使点 B 落在 BC 的延长线上的点 D处，且BDE 80，则B 度14（3 分）用科学记数法表示 0.00000105 为 15（3 分）已知 6m2，6 n3，则 63m+2n 16（3 分）已知一张三角形纸片 ABC（如图甲），其中 ABAC将纸片沿过点 B 的直线折叠，使点 C 落到 AB 边上的 E 点处，折痕为 BD（如图乙）再将纸片沿过点 E 的直线折叠，点 A 恰好与点 D 重合，折痕为 EF（如图丙）原三角形纸片 ABC 中，ABC 的大小为 三、解答题（共 72 分）17计算： 18解分式方程： + 1
5、9分解因式：（1）5a 2+10ab；（2）ax 24axy+4ay 220已知 a+b0，求代数式 a（a+4b）（a+2 b）（a2b）的值21列方程解应用题八年级学生去距学校 10km 的博物馆参观，一部分学生骑自行车先走，过了 20min 后，其余学生乘汽车出发，结果他们同时到达已知汽车的速度是骑车学生速度的 2 倍，求骑车学生的速度22如图，点 D、E 在ABC 的 BC 边上，ABAC ，ADAE求证：BDCE23周末，老师带同学去北京植物园中的一二九运动纪念广场，这里有三座侧面为三角形的纪念亭，挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神基于纪念亭的几何特征，同学们编拟了如下的
6、数学问题：如图 1，点 A，B，C，D 在同一条直线上，在四个论断“EAED ，EFAD，AB DC，FBFC ”中选择三个作为已知条件，另一个作为结论，构成真命题（补充已知和求证），并进行证明已知：如图，点 A，B，C，D 在同一条直线上， 求证： 证明： 24如图，A，B 分别为 CD，CE 的中点，AECD 于点 A，BDCE 于点 B求AEC 的度数25阅读材料小明遇到这样一个问题：求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数小明想通过计算（x+2）（2x+3）（3x+4）所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法他决定从简单情况开
7、始，先找（x+2）（2x+3）所得多项式中的一次项系数通过观察发现：也就是说，只需用 x+2 中的一次项系数 1 乘以 2x+3 中的常数项 3，再用 x+2 中的常数项 2 乘以2x+3 中的一次项系数 2，两个积相加 13+227，即可得到一次项系数延续上面的方法，求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数可以先用 x+2 的一次项系数 1，2x+3 的常数项 3，3x+4 的常数项 4，相乘得到 12；再用 2x+3 的一次项系数2，x+2 的常数项 2，3x +4 的常数项 4，相乘得到 16；然后用 3x+4 的一次项系数 3，x+2 的常数项 2，2x+3 的常
8、数项 3，相乘得到 18最后将 12，16，18 相加，得到的一次项系数为 46参考小明思考问题的方法，解决下列问题：（1）计算（2x+1）（3x +2）所得多项式的一次项系数为 （2）计算（x+1）（3x +2）（4x3）所得多项式的一次项系数为 （3）若计算（x 2+x+1）（x 23x +a）（2x 1）所得多项式的一次项系数为 0，则 a （4）若 x23x+1 是 x4+ax2+bx+2 的一个因式，则 2a+b 的值为 参考答案与试题解析一、选择题（每小题 3 分，共 30 分）1解：A、B 、C 均不是高线故选：D2解：第一个图形不是轴对称图形，第二个图形是轴对称图形，第三个图形
9、是轴对称图形，第四个图形不是轴对称图形，第五个图形不是轴对称图形，第六个图形是轴对称图形，综上所述，是轴对称图形的有 3 个故选：C3解： ，故选：B4解：将 0.056 用科学记数法表示为 5.6102 ，故选：B5解：A、b 5b3b 2，正确；B、（b 5） 2b 10，错误；C、b 2b4b 6，错误；D、a（a2b）a 22ab，错误；故选：A6解：大正方形的面积小正方形的面积a 2b 2，矩形的面积（a+b）（ab），故 a2b 2（a+b）（ab）故选：A7解：等腰三角形的顶角为 80，它的一个底角为（18080）250故选：B8解：A、a（x y ）axay，是整式乘法运算，故
10、此选项错误；B、x 2 4x+3x （x4）+3 ，不符合分解因式的定义，故此选项错误；C、a 2b 2（a+ b）（ab），是分解因式，符合题意；D、a 2+1a（ a+ ），不符合分解因式的定义，故此选项错误；故选：C9解：设小李每小时走 x 千米，依题意得： ，故选：B10解：DCAC 于 C，DE AB 于 E，并且 DEDC，12（到角的两边距离相等的点在这个角的平分线上）故选：C二、填空题（每小题 3 分，共 18 分）11解：ABCADE，ABAD ，BACDAE，BACDACDAEDAC，BADEAC，EAC40，BAD40，ABAD ，BADB （180BAD）70，故答案为
11、：7012解：3x 26x +3，3（x 22x+1），3（x1） 213解：ABC 绕点 A 逆时针旋转至ADE 处，BADE ，ABAD，BADB ，BDEADB+ADE ，BDE2B ，B BDE 8040故答案为 4014解：0.000001051.0510 6 ，故答案为：1.0510 6 15解：6 m2，6 n3，则 63m+2n（6 m） 3（6 n） 28972故答案为：7216解：设Ax ，根据翻折不变性可知AEDA x，CBEDA+EDA2x，ABAC，ABCC2x，A+ABC+C 180，5x180，x36，ABC72故答案为 72三、解答题（共 72 分）17解：原式
12、 18解：去分母得：5（x3）+2x+35x15+2x +3x4经检验：x4 是原分式方程的解19解：（1）5a 2+10ab5a（a+2b）；（2）ax 24axy+4ay 2a（x 24xy+4y 2）a（x2y） 220解：当 a+b0 时，原式a 2+4aba 2+4b24ab+4b 24b（a+b）021解：设骑车学生的速度为 xkm/h，由题意得， ，解得：x15经检验：x15 是原方程的解答：骑车学生的速度为 15km/h22证明：如图，过点 A 作 APBC 于 PABAC，BPPC；ADAE，DPPE，BPDP PC PE，BDCE23解：已知：如图，EAED，EFAD，AB
13、DC，求证 FBFC理由：延长 EF 交 BC 于 HEAED ，EFAD，AHHD ，ABDC，BHCH，FHBC，FBFC故答案为：EAED ，EFAD，ABDC；FBFC ；延长 EF 交 BC 于 HEAED ，EFAD，AHHD ，ABDC，BHCH，FHBC，FBFC24解：连接 DEA，B 分别为 CD，CE 的中点，AECD 于点 A，BD CE 于点 B，CDCEDE，CDE 为等边三角形C60AEC90C3025解：（1）（2x+1）（3x+2）所得多项式的一次项系数为 22+137，故答案为：7；（2）（x+1）（3x +2）（4x 3）所得多项式的一次项系数为 12（3）+13（3）+1247，故答案为：7；（3）（x 2+x+1）（x 23x +a）（2x 1）所得多项式的一次项系数为 1a（1）+1（3）（1）+1 a2a+3 ，由题意知 a+30，解得：a3，故答案为：3；（4）由 x4+ax2+bx+2 中 4 次项系数为 1、常数项为 2 可设另一个因式为 x2+mx+2，则（x 23x+1）（ x2+mx+2）x 4+ax2+bx+2， ，解得： ，2a+b12315，故答案为：15
