 陕西省2019年中考数学真题试题(含解析)
陕西省2019年中考数学真题试题(含解析)
《陕西省2019年中考数学真题试题(含解析)》由会员分享,可在线阅读,更多相关《陕西省2019年中考数学真题试题(含解析)(25页珍藏版)》请在七七文库上搜索。
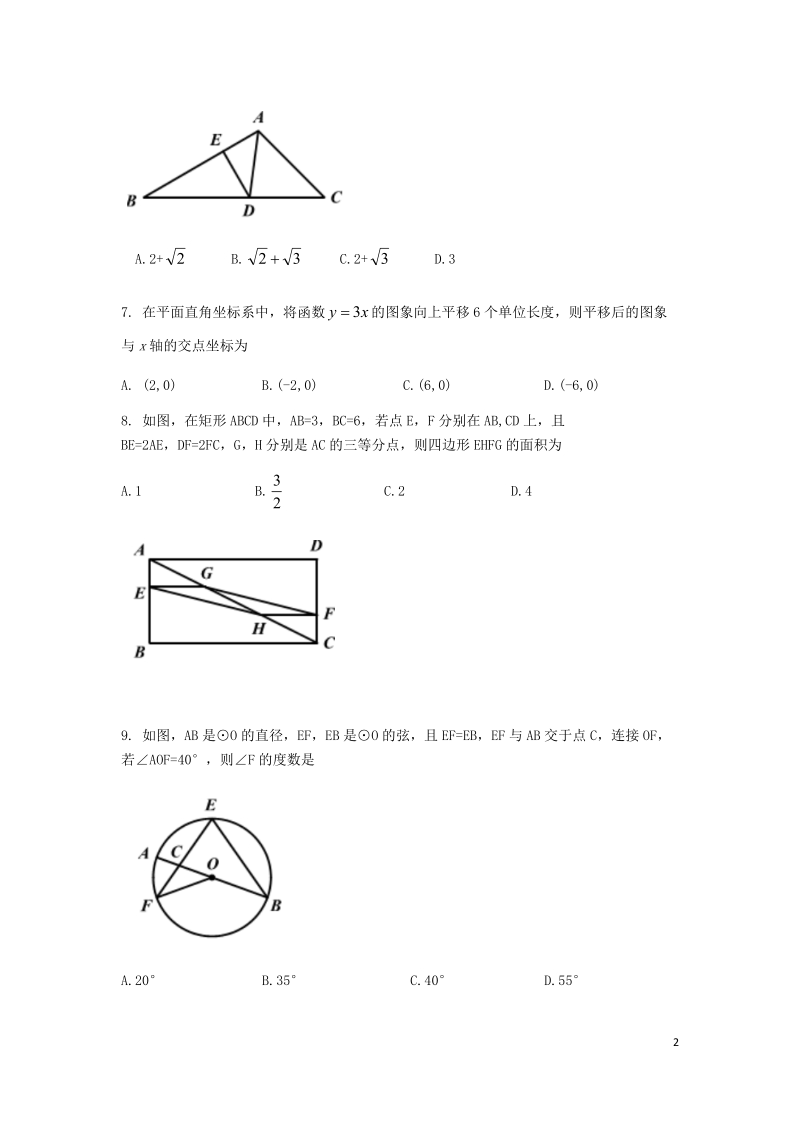
1、12019年陕西中考数学1、选择题(共 10小题,每小题 3分,共 30分)1. 计算: 03- A.1 B.0 C. 3 D. 312. 如图,是由两个正方体组成的几何体,则该几何体的俯视图为 3. 如图,OC 是AOB 的角平分线, l/OB,若1=52,则2 的度数为A.52 B.54 C.64 D.694. 若正比例函数 xy2的图象经过点 O( a-1,4),则 a的值为A. -1 B.0 C.1 D.25. 下列计算正确的是A. 2263a B.24263baC.22b D. 226. 如图,在ABC 中,B=30,C=45,AD 平分BAC 交 BC于点 D,DEAB,垂足为E。
2、若 DE=1,则 BC的长为2A.2+ 2 B. 3 C.2+ 3 D.3 7. 在平面直角坐标系中,将函数 xy的图象向上平移 6个单位长度,则平移后的图象与 x轴的交点坐标为A. (2,0) B.(-2,0) C.(6,0) D.(-6,0)8. 如图,在矩形 ABCD中,AB=3,BC=6,若点 E,F 分别在 AB,CD上,且BE=2AE,DF=2FC,G,H 分别是 AC的三等分点,则四边形 EHFG的面积为A.1 B. 23 C.2 D.49. 如图,AB 是O 的直径,EF,EB 是O 的弦,且 EF=EB,EF 与 AB交于点 C,连接 OF,若AOF=40,则F 的度数是A.
3、20 B.35 C.40 D.55310. 在同一平面直角坐标系中,若抛物线 4212mxxy与nxmy32关于 y轴对称,则符合条件的 m,n 的值为A. m= 75,n= 18- B.m=5,n= -6 C.m= -1,n=6 D.m=1,n= -22、填空题(共 4小题,每小题 3分,共 12分)11. 已知实数 21,0.16, , , 25, 34,其中为无理数的是 12. 若正六边形的边长为 3,则其较长的一条对角线长为 13. 如图,D 是矩形 AOBC的对称中心,A(0,4),B(6,0) ,若一个反比例函数的图象经过点 D,交 AC于点 M,则点 M的坐标为 14. 如图,在
4、正方形 ABCD中,AB=8,AC 与 BD交于点 O,N 是 AO的中点,点 M在 BC边上,且 BM=6. P为对角线 BD上一点,则 PMPN的最大值为 43、解答题(共 78分)15. (5 分)计算:231-27-16. (5 分)化简: aa248217. (5 分)如图,在ABC 中,AB=AC,AD 是 BC边上的高。请用尺规作图法,求作ABC的外接圆。 (保留作图痕迹,不写做法)18. (5 分)如图,点 A,E,F 在直线 l上,AE=BF,AC/BF,且 AC=BD,求证:CF=DE519. (7 分)本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅
5、怀革命先烈,奋斗新时代”为主题的读书活动。校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量” (下面简称:“读书量” )进行了随机抽样调查,并对所有随机抽取学生的“读书量” (单位:本)进行了统计,如下图所示:所抽取该校七年级学生四月份“读书量”的统计图根据以上信息,解答下列问题:(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 (2)求本次所抽取学生四月份“读书量”的平均数;(3)已知该校七年级有 1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数。620. (7 分)小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习
6、小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部 B,如图所示。于是他们先在古树周围的空地上选择一点 D,并在点 D处安装了测量器DC,测得古树的顶端 A的仰角为 45;再在 BD的延长线上确定一点 G,使 DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着 BG方向移动,当移动带点 F时,他刚好在小平面镜内看到这棵古树的顶端 A的像,此时,测得 FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度 CD=0.5米。已知点 F、G、D、B 在同一水平直线上,且EF、CD、AB 均垂直于 FB,求这棵古树的高度 AB。 (小平面镜的大小忽略不计)21
7、. (7 分)根据记录,从地面向上 11km以内,每升高 1km,气温降低 6;又知在距离地面 11km以上高空,气温几乎不变。若地面气温为 m() ,设距地面的高度为 x(km)处的气温为 y()(1)写出距地面的高度在 11km以内的 y与 x之间的函数表达式;(2)上周日,小敏在乘飞机从上海飞回西安图中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为26时,飞机距离地面的高度为 7km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面 12km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面 12km时,飞机外的气温。722. (7 分)现有 A、B 两个
8、不透明袋子,分别装有 3个除颜色外完全相同的小球。其中,A袋装有 2个白球,1 个红球;B 袋装有 2个红球,1 个白球。(1)将 A袋摇匀,然后从 A袋中随机取出一个小球,求摸出小球是白色的概率;(2)小华和小林商定了一个游戏规则:从摇匀后的 A,B 两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。23. (8 分)如图,AC 是O 的一条弦,AP 是O 的切线。作 BM=AB并与 AP交于点 M,延长 MB交 AC于点 E,交O 于点 D,连接 AD。(1)求证:AB=BE(2)若O 的半
9、径 R=5,AB=6,求 AD的长。824. (10 分)在平面直角坐标系中,已知抛物线 L: cxay2经过点 A(-3,0)和点 B(0,-6) ,L 关于原点 O堆成的抛物线为 (1)求抛物线 L的表达式(2)点 P在抛物线 上,且位于第一象限,过点 P作 PDy 轴,垂足为 D。若POD 与AOB相似,求复合条件的点 P的坐标25. (12 分)问题提出:9(1)如图 1,已知ABC,试确定一点 D,使得以 A,B,C,D 为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:(2)如图 2,在矩形 ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的BPC,且使B
10、PC90,求满足条件的点 P到点 A的距离;问题解决:(3)如图 3,有一座草根塔 A,按规定,要以塔 A为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区 BCDE。根据实际情况,要求顶点 B是定点,点 B到塔 A的距离为 50米,CBE=120,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形 BCDE的最大面积;若不可以,请说明理由。(塔 A的占地面积忽略不计)102019年陕西中考数学4、选择题(共 10小题,每小题 3分,共 30分)26. 计算: 03- A.1 B.0 C. 3 D. 31【解析】本题考查 0指数幂, )0(
11、10a,此题答案为 1,故选 A27. 如图,是由两个正方体组成的几何体,则该几何体的俯视图为 【解析】本题考查三视图,俯视图为从上往下看,所以小正方形应在大正方形的右上角,故选 D 28. 如图,OC 是AOB 的角平分线, l/OB,若1=52,则2 的度数为A.52 B.54 C.64 D.69【解析】 l/OB,1+AOB=180,AOB=128,OC 平分AOB,BOC=64,又 l/OB,且2 与BOC 为同位角,2=64,故选 C29. 若正比例函数 xy2的图象经过点 O( a-1,4),则 a的值为B. -1 B.0 C.1 D.211【解析】函数 xy2过 O( a-1,4
12、) , 4)1(2a, 1a,故选 A30. 下列计算正确的是B. 2263a B.24263baC.22b D. 22【解析】A 选项正确结果应为 4263a,B 选项正确结果应为 249ba,C 选项为完全平方差公式,正确结果应为 ba,故选 D31. 如图,在ABC 中,B=30,C=45,AD 平分BAC 交 BC于点 D,DEAB,垂足为 E。若 DE=1,则 BC的长为A.2+ 2 B. 3 C.2+ 3 D.3 【解析】过点 D作 DFAC 于 F如图所示,AD 为BAC 的平分线,且 DEAB 于 E,DFAC 于F,DE=DF=1,在 RtBED 中,B=30,BD=2DE=
13、2,在 RtCDF 中,C=45,CDF为等腰直角三角形,CD= 2DF= ,BC=BD+CD= 2,故选 A32. 在平面直角坐标系中,将函数 xy3的图象向上平移 6个单位长度,则平移后的图象与 x轴的交点坐标为B. (2,0) B.(-2,0) C.(6,0) D.(-6,0)12【解析】根据函数图象平移规律,可知 xy3向上平移 6个单位后得函数解析式应为63xy,此时与 x轴相交,则 0, 0,即 2x,点坐标为(-2,0) ,故选 B33. 如图,在矩形 ABCD中,AB=3,BC=6,若点 E,F 分别在 AB,CD上,且BE=2AE,DF=2FC,G,H 分别是 AC的三等分点
14、,则四边形 EHFG的面积为A.1 B. 23 C.2 D.4【解析】 BE2 AE, DF2 FC, G、 H分别是 AC的三等分点 E是 AB的三等分点, F是 CD的三等分点 EG BC且 EG BC213同理可得 HF AD且 HF AD213四边形 EHFG为平行四边形 EG和 HF间距离为 1S 四边形 EHFG21=2,故选 C34. 如图,AB 是O 的直径,EF,EB 是O 的弦,且 EF=EB,EF 与 AB交于点 C,连接 OF,若AOF=40,则F 的度数是13A.20 B.35 C.40 D.55【解析】连接 FB,得到 FOB140; FEB70 EF EB EFB

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 数学 中考真题
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-76996.html