1、1相交线与平行线_1.掌握对顶角和邻补角的概念；2.掌握垂线段的定义及其画法；3.掌握三线八角的定义和找法；4.掌握平行线的性质与判定.1.相交线（1 ） 在同一平面内，两条直线的位置关系有_ 和_。（2 ）相交：在同一平面内，有_的两条直线称为相交线。（3）邻补角：定义：有公共顶点，且有一条公共边，另一条边互为反向延长线，具有这种位置关系的两个角，互为邻补角。性质：位置 互为邻角 数量 互为补角（两角之和为 180）（4）对顶角：定义：有一个公共顶点，并且有一个角的两边分别是另一个角两边的反向延长线，具有这种位置关系的两个角，互为对顶角性质： 对顶角相等 几何语言：1+ 2=1802+3=1
2、801=3（同角的补角相等）两直线相交所成的四个角中存在几种不同关系的角，它们的概念及性质如下表：图形 顶点 边的关系 大小关系对顶角1 与2有公共顶点 1 的两边与 2 的两边互为反向延长线对顶角相等即1= 2邻补角3 与4有公共顶点 3 与4 有一条边公共，另一边互为反向延长线。3+4=180注意点：对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；如果 与 是对顶角，那么一定有= ；反之如果 =，那么 与 不一定是对顶1 24 32角如果 与 互为邻补角，则一定有_；反之如果+ =180，则 与 不一定是邻补角。（4 ）两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一
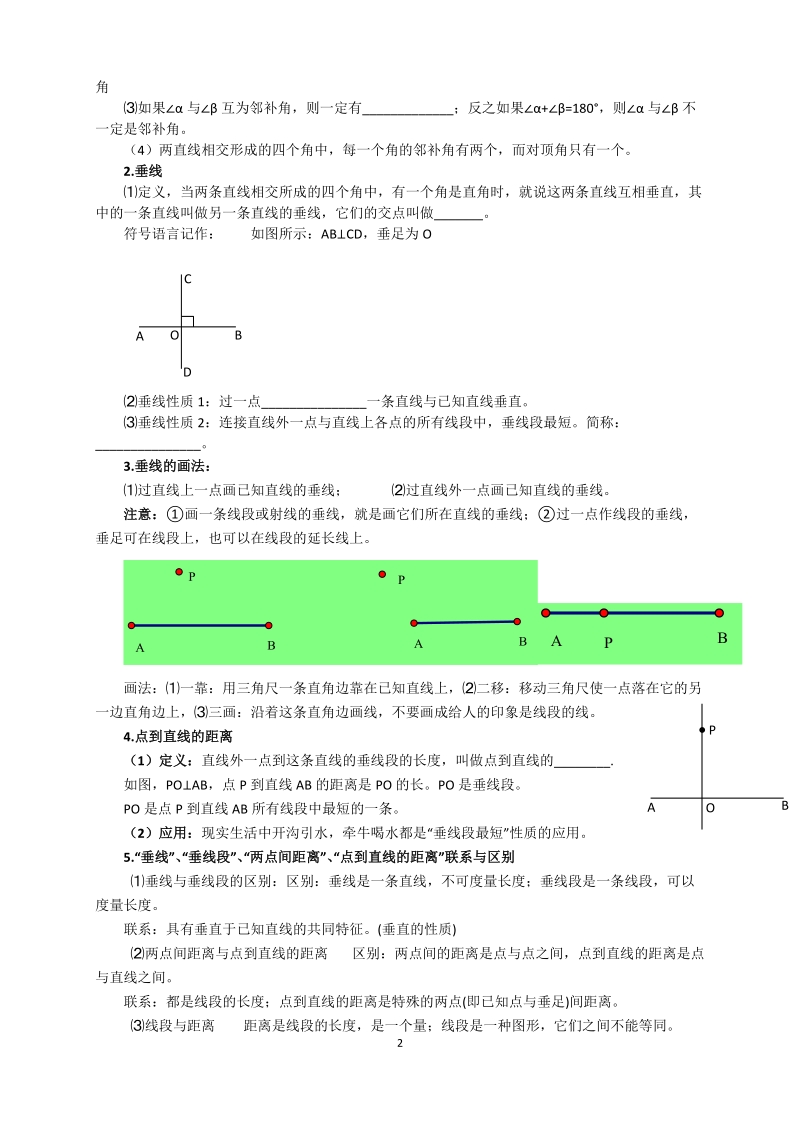
3、个。2.垂线定义，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做_。符号语言记作： 如图所示：AB CD，垂足为 O垂线性质 1：过一点_一条直线与已知直线垂直。 垂线性质 2：连接直线外一点与直线上各点的所有线段中，垂线段最短。简称：_。3.垂线的画法：过直线上一点画已知直线的垂线； 过直线外一点画已知直线的垂线。注意：画一条线段或射线的垂线，就是画它们所在直线的垂线；过一点作线段的垂线，垂足可在线段上，也可以在线段的延长线上。BABAPP画法：一靠：用三角尺一条直角边靠在已知直线上，二移：移动三角尺使一点落在它的另
4、一边直角边上，三画：沿着这条直角边画线，不要画成给人的印象是线段的线。4.点到直线的距离（1 ）定义：直线外一点到这条直线的垂线段的长度，叫做点到直线的_.如图，PO AB，点 P 到直线 AB 的距离是 PO 的长。PO 是垂线段。PO 是点 P 到直线 AB 所有线段中最短的一条。（2 ）应用：现实生活中开沟引水，牵牛喝水都是 “垂线段最短” 性质的应用。5.“垂线”、 “垂线段”、 “两点间距离”、 “点到直线的距离”联系与区别垂线与垂线段的区别：区别：垂线是一条直线，不可度量长度；垂线段是一条线段，可以度量长度。 联系：具有垂直于已知直线的共同特征。(垂直的性质)两点间距离与点到直线的
5、距离 区别：两点间的距离是点与点之间，点到直线的距离是点与直线之间。 联系：都是线段的长度；点到直线的距离是特殊的两点(即已知点与垂足 )间距离。线段与距离 距离是线段的长度，是一个量；线段是一种图形，它们之间不能等同。A BCDOPA BOP BA334 l3l2l1126.三线八角两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角。如图，直线 ba,被直线 l所截（1 ） 1 与5 在截线 的同侧，同在被截直线 ba,的上方，叫做_（位置相同）（2 ） 5 与3 在截线 l的两旁（交错） ，在被截直线 ,之间（内） ，叫做_（位置在内且交错）（3 ） 5 与4 在截线
6、l的同侧，在被截直线 ba,之间（内） ，叫做_。（4 ）三线八角也可以成模型中看出。同位角是“A” 型；内错角是“Z”型；同旁内角是“U”型。1.对顶角、邻补角【例 1】 （2017 广西柳州）如图，图中 的度数等于（ ）A 135 B 125 C 115D 105【解析】此题考查邻补角定义，根据邻补角互补解答即可解： 的度数=18045=135【答案】A练习 1.下列说法正确的有( )对顶角相等;相等的角是对顶角;若两个角不相等 ,则这两个角一定不是对顶角;若两个角不是对顶角,则这两个角不相等.A.1 个 B.2 个 C.3 个 D.4 个练习 2.如图所示，直线 AB，CD，EF 相交于
7、点 O，AOD 的对顶角是_，AOC 的邻补角是 ；若 AOC50，则BOD _，COB _OFE DCBA练习 3.对顶角的性质是_练习 4.如果 CDAB 于点 D，自 CD 上任一点向 AB 作垂线，那么所画垂线均与 CD 重合，这是因为 练习 5.如图所示,L 1,L2,L3 交于点 O,1=2,3:1=8:1,求4 的度数.( 方程思想)abl123 4567 842.垂线段【例 2】画 A30 ，在 A 的两边上分别截取 AC40mm，AB 26mm，连结 BC，过 C 点分别画 CA，AB 的垂线，画 B 点到 AC 的垂线段，并量出 C 点到 AB 的距离和 B 点到 AC 的
8、距离.【解析】根据题意作图，再根据垂线段的定义，作出距离，量出线段长度即可。【答案】如图，C 点到 AB 的距离 CE20，B 点到 AC 的距离 BF13.练习 6.如图所示，下列说法不正确的是 ( )A.点 B 到 AC 的垂线段是线段 AB； B.点 C 到 AB 的垂线段是线段 AC；C.线段 AD 是点 D 到 BC 的垂线段； D.线段 BD 是点 B 到 AD 的垂线段.D CBA练习 7.如图所示，AD BD，BC CD，ABa，BCb，则 BD 的范围是 ，理由是 . DCBA练习8.如图，线段AB的长是 到 的距离；点D到AB 的距离是 的长；线段_的长是点B到AC 的距离
9、.3.三线八角（同位角、内错角、同旁内角）【例 3】 （2017江苏宿迁，第 4 题）如图所示，直线 a， b 被直线 c 所截， 1 与 2 是（ ）5A同位角 B 内错角 C 同旁内角 D 邻补角 .【解析】根据三线八角的概念，以及同位角的定义作答即可解：如图所示，1 和 2 两个角都在两被截直线直线 b 和 a 同侧，并且在第三条直线c（截线）的同旁，故 1 和2 是直线 b、a 被 c 所截而成的同位角【答案】A练习 9.如图，A 的同位角是_，1 的内错角是_，2 的同旁内角是_ 如图所示，B 与 CAD 是由直线 _与直线_ 被直线_所截得到的_角练习 10.如图：(1) 1 和
10、B 是由直线 截直线 和 所成的 角.(2)2 和C 是由直线 截直线 和 所成的 角.(3)B 和C 是由直线 截直线 和 所成的 角 .练习11. 如图，(1) B、 EDB是直线 和 被直线 所截得 角；(2)直线 截直线 和 所得的 AFD和C是 角；(3)与 CFD成内错角的有 ；(4)与 C成同旁内角的有 个，它们是 .61 若一个角的两边分别与另一个角的两边互相垂直，则这两个角 .2已知点 O，画和点 O 的距离是 3 厘米的直线可以画条.3如图，O 是直线 AB 上一点，COB30 ，则14平面上三条直线两两相交最多能构成对顶角的对数是 .5下列说法正确的个数是（ ）如果两个角
11、相等，那么这两个角是对顶角；对顶角的平分线在同一条直线上；如果两个角有公共顶点，且角平分线互为反向延长线，那么这两个角是对顶角；两个有公共顶点的角相等，且一个角的一边是另一个角一边的反向延长线，那么这两个角是对顶角A、1 个 B、2 个 C、3 个 D、4 个6.如图，直线AB、CD相交于O，OE CD，OF 平分BOC，AOC30，则BOE ， COF ，EOF ，AOE .7.如图，已知OAOB，ODOC，则下列说法不正确的是( )A.BOC AODB.AOC+BOD 180C.COD与AOB互补D.COB与BOD相等8.（2011梧州）如图，直线 EOCD，垂足为点 O，AB 平分EOD
12、，则 BOD 的度数为（ ）A120 B130C 135 D1407DCBA9.如图，直线 AB、CD 相交于点 O，作DOEBOD，OF 平分 AOE，若AOC28，则EOF度10.如图，直线 AB、CD 被直线 EF 所截，则3 的同旁内角是（ B ） A1 B2 C4 D5345CDEF11.下列说法中错误的个数是（ ）（1）过一点有且只有一条直线与已知直线平行。（2）过一点有且只有一条直线与已知直线垂直。（3）在同一平面内，两条直线的位置关系只有相交、平行两种。（4）不相交的两条直线叫做平行线。（5）有公共顶点且有一条公共边的两个角互为邻补角。A. 1 个 B. 2 个 C. 3 个
13、D. 4 个 12.如右图所示，已知 ， ，垂足分别是 、 ，那 BCAD么以下线段大小的比较必定成立的是（ ）A. B. DCC. D. B13如图，CD AB，垂足为 D，ACBC ，垂足为 C图中线段的长能表示点到直线（或线段）距离的线段有（ ）（A）1 条 （B）3 条 （C ）5 条 （D）7 条14、如图，ADBC，点 O 在 AD 上，BO、CO 分别平分ABC 、DCB，若ADm 则BOC _OFEDC BA8第 14 题 第 15 题 15、三条直线 、 、 相交于点 ，如图所示， 的对顶角是 ABCDEFOAOD， 的对顶角是 ， 的邻补角是 。FO_1如图，三条直线 AB
14、，CD，EF 相交于点 O，则AOE+DOB+ COF O FE DCBA2 （ 2017柳州）如图，在所标识的角中，互为对顶角的两个角是（ ）A2 和 3 B1 和3 C1 和4 D1 和23两条相交直线所成的角中( )A必有一个钝角 B必有一个锐角C必有一个不是钝角 D必有两个锐角4 （ 2018梧州）如图，直线 a、b 相交，165，则2 的度数是5如图所示，直线 AB，CD 相交于点 O，已知 AOC70，OE 把BOD 分成两部分，且BOE：EOD2：3，则EOD_O EDC BA6两条直线相交于一点构成 对对顶角；三条直线相交于一点，构成 对对顶角；n 直线相交于一点，构成 对对顶
15、角；100 条直线相交于一点构成 对对顶角.7平面上三条直线相互间的交点个数是 ；平面上四条直线相互间的交点个数是 98点 P 为直线 m 外一点，点 A，B，C 为直线 m 上三点， PA4cm，PB5cm ，PC2cm，则点 P 到 直线 m 的距离为( )A4cm B2cmC小于 2cm D不大于 2cm9如图， 1 的同旁内角有 个10对于下图，有以下判断： 1 与3 是内错角；2 与3 是内错角； 2 与 4 是同旁内角；2 与 3 是同位角其中说法正确的有 (填写序号) 11.如图所示，能表示点到直线( 线段)的距离的线段有 条D CBA12如图，ACBC，AC 9，BC12，AB15（1 ）试说出点 A 到直线 BC 的距离；点 B 到直线 AC 的距离；（2 ）点 C 到直线 AB 的距离是多少？你是怎样求得的？1013如图所示，l 1，l 2，l 3 交于点 O，12，3：1 8：1，求4 的度数34 l3l2l112
