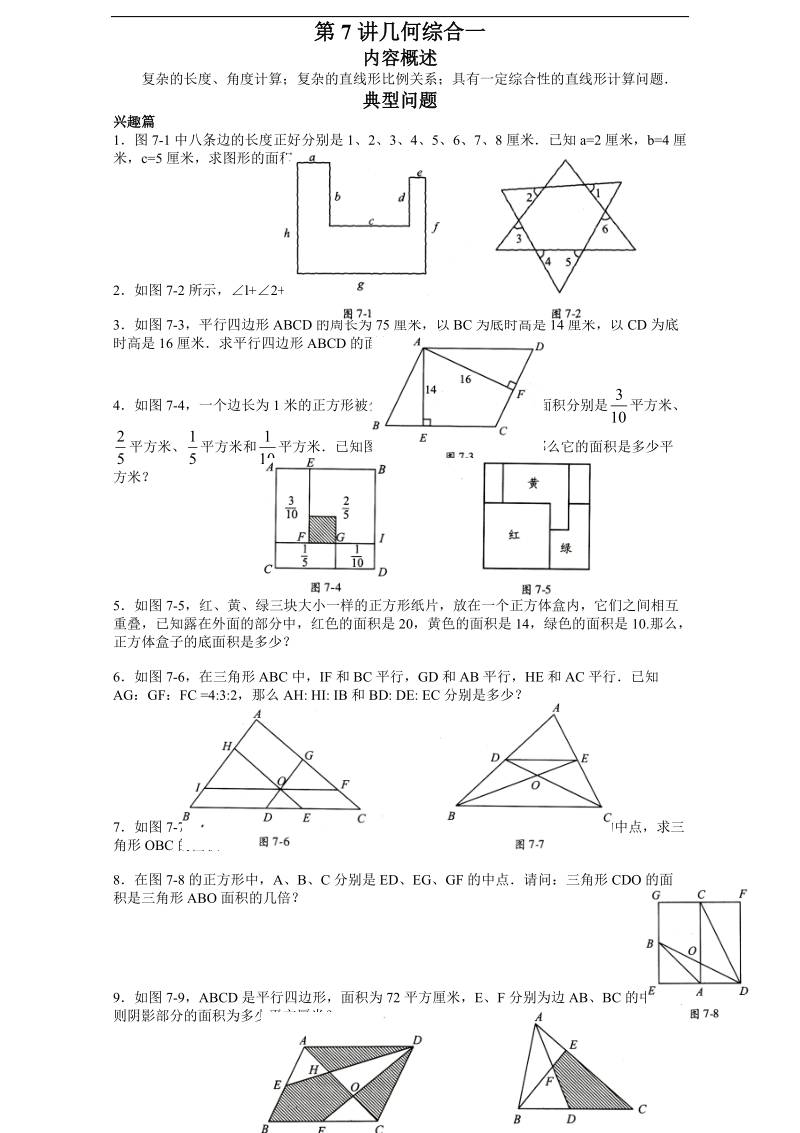
1、第 7 讲几何综合一内容概述复杂的长度、角度计算；复杂的直线形比例关系；具有一定综合性的直线形计算问题典型问题兴趣篇1图 7-1 中八条边的长度正好分别是 1、2、3、4、5、6、7、8 厘米已知 a=2 厘米，b=4 厘米，c=5 厘米，求图形的面积2如图 7-2 所示，l+2+3+4+ 5+6 等于多少度？3如图 7-3，平行四边形 ABCD 的周长为 75 厘米，以 BC 为底时高是 14 厘米，以 CD 为底时高是 16 厘米求平行四边形 ABCD 的面积。4如图 7-4，一个边长为 1 米的正方形被分成 4 个小长方形，它们的面积分别是 平方米、103平方米、 平方米和 平方米已知图
2、中的阴影部分是正方形，那么它的面积是多少平520方米？5如图 7-5，红、黄、绿三块大小一样的正方形纸片，放在一个正方体盒内，它们之间相互重叠，已知露在外面的部分中，红色的面积是 20，黄色的面积是 14，绿色的面积是 10.那么，正方体盒子的底面积是多少？6如图 7-6，在三角形 ABC 中，IF 和 BC 平行，GD 和 AB 平行，HE 和 AC 平行已知AG：GF：FC =4:3:2，那么 AH: HI: IB 和 BD: DE: EC 分别是多少？7如图 7-7，已知三角形 ABC 的面积为 1 平方厘米，D 、 E 分别是 AB、AC 边的中点，求三角形 OBC 的面积8在图 7-
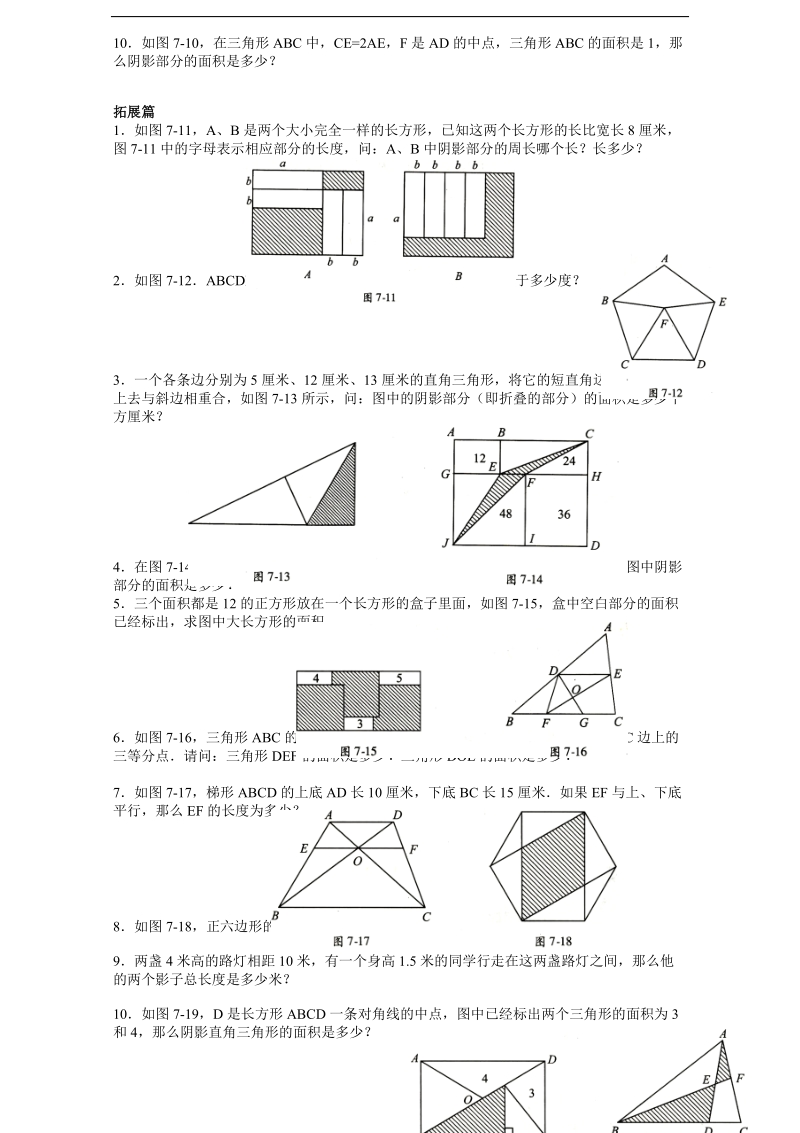
3、8 的正方形中，A、B 、C 分别是 ED、EG 、GF 的中点请问：三角形 CDO 的面积是三角形 ABO 面积的几倍？9如图 7-9，ABCD 是平行四边形，面积为 72 平方厘米，E、F 分别为边 AB、BC 的中点，则阴影部分的面积为多少平方厘米？10如图 7-10，在三角形 ABC 中，CE=2AE，F 是 AD 的中点，三角形 ABC 的面积是 1，那么阴影部分的面积是多少？拓展篇1如图 7-11，A、B 是两个大小完全一样的长方形，已知这两个长方形的长比宽长 8 厘米，图 7-11 中的字母表示相应部分的长度，问： A、B 中阴影部分的周长哪个长？长多少？2如图 7-12ABCD
4、E 是正五边形， CDF 是正三角形，BFE 等于多少度？3一个各条边分别为 5 厘米、12 厘米、13 厘米的直角三角形，将它的短直角边对折到斜边上去与斜边相重合，如图 7-13 所示，问：图中的阴影部分（即折叠的部分）的面积是多少平方厘米？4在图 7-14 中大长方形被分为四个小长方形，面积分别为 12、24、36、48.请问：图中阴影部分的面积是多少？5三个面积都是 12 的正方形放在一个长方形的盒子里面，如图 7-15，盒中空白部分的面积已经标出，求图中大长方形的面积6如图 7-16，三角形 ABC 的面积为 1D 、E 分别为 AB、AC 的中点F、G 是 BC 边上的三等分点请问：
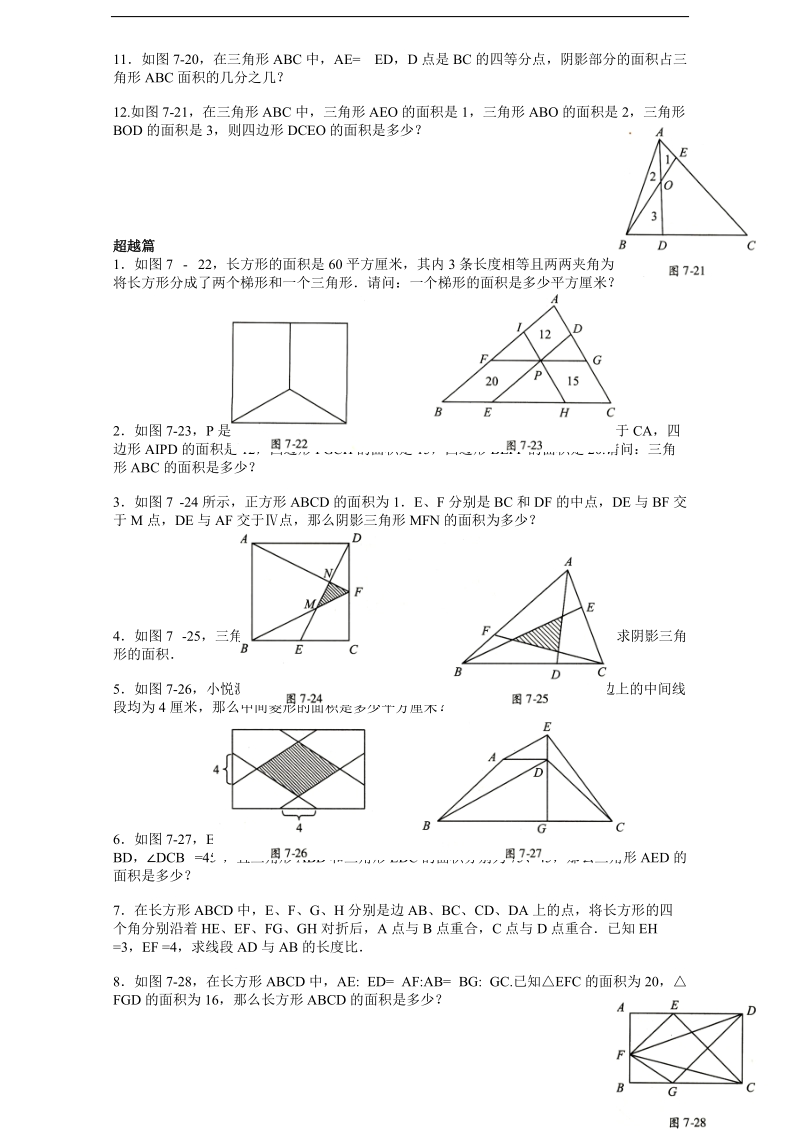
5、三角形 DEF 的面积是多少？三角形 DOE 的面积是多少？7如图 7-17，梯形 ABCD 的上底 AD 长 10 厘米，下底 BC 长 15 厘米如果 EF 与上、下底平行，那么 EF 的长度为多少？8如图 7-18，正六边形的面积为 6，那么阴影部分的面积是多少？9两盏 4 米高的路灯相距 10 米，有一个身高 1.5 米的同学行走在这两盏路灯之间，那么他的两个影子总长度是多少米？10如图 7-19，D 是长方形 ABCD 一条对角线的中点，图中已经标出两个三角形的面积为 3和 4，那么阴影直角三角形的面积是多少？11如图 7-20，在三角形 ABC 中，AE= ED，D 点是 BC 的
6、四等分点，阴影部分的面积占三角形 ABC 面积的几分之几？12.如图 7-21，在三角形 ABC 中，三角形 AEO 的面积是 1，三角形 ABO 的面积是 2，三角形BOD 的面积是 3，则四边形 DCEO 的面积是多少？超越篇1如图 7 - 22，长方形的面积是 60 平方厘米，其内 3 条长度相等且两两夹角为 120的线段将长方形分成了两个梯形和一个三角形请问：一个梯形的面积是多少平方厘米？2如图 7-23，P 是三角形 ABC 内一点，DE 平行于 AB，FG 平行于 BC，HI 平行于 CA，四边形 AIPD 的面积是 12，四边形 PGCH 的面积是 15，四边形 BEPF 的面积
7、是 20.请问：三角形 ABC 的面积是多少？3如图 7 -24 所示，正方形 ABCD 的面积为 1E、F 分别是 BC 和 DF 的中点，DE 与 BF 交于 M 点，DE 与 AF 交于点，那么阴影三角形 MFN 的面积为多少？4如图 7 -25，三角形 ABC 的面积为 1，D、E、F 分别是三条边上的三等分点，求阴影三角形的面积5如图 7-26，小悦测出家里瓷砖的长为 24 厘米，宽为 10 厘米，而且还测出了边上的中间线段均为 4 厘米，那么中间菱形的面积是多少平方厘米？6如图 7-27，ED 垂直于等腰梯形 ABCD 的上底 AD，并交 BC 于 G，AE 平行于BD，DCB =
8、45，且三角形 ABD 和三角形 EDC 的面积分别为 75、45，那么三角形 AED 的面积是多少？7在长方形 ABCD 中，E、F、G、H 分别是边 AB、BC、CD、DA 上的点，将长方形的四个角分别沿着 HE、EF、FG、GH 对折后，A 点与 B 点重合，C 点与 D 点重合已知 EH =3，EF =4，求线段 AD 与 AB 的长度比8如图 7-28，在长方形 ABCD 中，AE: ED= AF:AB= BG: GC.已知EFC 的面积为 20，FGD 的面积为 16，那么长方形 ABCD 的面积是多少？第 7 讲 几 何 综 合 一兴 趣 篇1. 图中八条边的长度正好 分别是 1
9、、 2、 3、 4、 5、 6、 7、 8 厘米 。 已知a 2厘米 ，b 4厘 米 ，c 5厘米 ， 求图形 的 面积 。【分析 】S 2 7 1 6 5 3 14 6 15 35(cm 2 )2. 如图所示 ， 1 2 3 4 5 6等于多少度 ？【分析 】将这六 个角 用中 心六 边形 的六个 内角 代换 ，利 用六 边形内 角和 为7 20 ，列方 程得(180 1) (180 2) (180 3) (180 4) (180 5) (180 6) 720 ， 所以 1 2 3 4 5) 6 3603. 如图 ， 平行四边形A BCD 的周长为 75 厘米 。 以B C 为底 时 高是
10、14 厘米 ， 以 CD 为底时高是 16厘米 。 求平行四边 形 ABCD 的面积 。221 【分析 】BC CD 75 2 37.5 ,根据面积相等 ，底的比与高的比成反比例， 所以BC : CD 16 : 14 8 : 7 ,因 此 BC 37.5 (8 7) 8 20 ,平 行 四 边 形 ABCD 的 面 积 是20 14 280 平方厘 米4. 如图所示 ， 一个边长 为1 米的正方形 被 分成 4个小长方形 ， 它们的 面积 分别是 3 平方10米 、 2平方米 、 1平方米和 1 平方米 。 已知图中的 阴影部 分是正方形 ， 那么 它的面 积是5 5 10多少平方米 ？【分析
11、 】CH1 5 2 ,因 此 CH 23, HD 1 , AE 10 3 ,所 以 AE 3 , EB 4 ,因 此HD 1 1103 3 EB 2 4 7 75FG 2 3 5 ,那么 它的 面积 是 5 25 平方米3 7 21 4415. 如图 ， 红 、 黄 、 绿三块 大小一样的正方形纸 片 ， 放在一个正方体盒内 ， 它 们之间相互重 叠 。 已知露在外面的 部分 中 ， 红色的面积是 20， 黄 色的面积是 14， 绿色的面 积是 10。那么 ， 正方体盒子的 底面 积是多少 ？黄红 绿【分析 】将黄色 纸片推到左边 ，则每块纸 片露出的形状如右上 图 .黄 、绿两色 的面积之和
12、 保 持14+10=24 不 变， 则 在右 图中 这 两块 面积 相等 ，均 为 24 2 12 .根 据公 式可 知 ， 空 白 处 面 积 黄 绿 红 12 12 20 7.2 ， 则 正 方 形 盒 底 面 积 是7.2 12 12 20 51.2 .6. 如图 ， 在三角形 ABC 中 ， IF 和B C 平行 ，G D 和A B 平行 ，HE 和A C 平行 。 已知 AG ：GF ：F C =4:3:2， 那么 AH ：HI ：I B 和B D ：DE ：E C 分别是多 少 ？ 9AHGI O FB D E C【分析 】连 接 AO, BO.CO ,设S AOG 4a ，则S2
13、 GOF 3a ，S COF 2a ，那 么S AOH 4a ，S COE 2a ，根 据 相 似2S GOFS AIF 3 7 = 949,所 以 S GOFSGOIA2 ,则 S HOI 40 16 a ，又3S GOF 3 9 ,所 以 S DOE 4 a ， S AIF 7 49 ,因 此SA BDOI 16 a ，那 么S GDC 5 25 3 S ABC 9 81 3S BOI S BOD 8 a3 ， 因 此AH : HI : IB 4a : 16 a : 8 a 3 : 4 : 2 BD DE EC 8 a : 4 a : 2a 4 2 33 3 3 37. 如图 ， 已知三角
14、形A BC 的面积为 1 平方厘米 ，D 、E 分别是A B 、A C 边的中点 ， 求三 角形O BC 的面积 。 ACD COD【分析 】因 为 DE 是 ABC 的 中线 ，所以 S 3 ,设S a ，根 据梯形 蝴蝶 定理有四 边 形 BCED 4 ODEa 2a 4a 2a 9a 3 ，所以 a 1 所以S 4 1 14 12 OBC 12 38. 在图中的正方形中 ，A 、B 、C 分别是E D 、E G 、G F 的中点 。 请 问 ： 三角形CDO 的 面积是三角形 ABO 面积的几倍 ？【分析 】设 正方 形的 面积 为 1 ，则 S 1 ,S ABO 1 S AOD ,所以
15、S 1 1 3 ,因4 16此 三角 形CDO 的面积 是三 角形 ABO 面积的3 倍4 16 169. 如图 ， ABCD 是平行四边 形 ， 面积为 72平方厘 米 ， E 、F 分别为边A B 、B C 的中点 ， 则阴影部分的面积为 多少 平方厘米 ？A G DO E HMB F C【分析 】设G 、H 分别为A D 、DC 的中点 ，连 接GH 、EF 、BD 可得SA AED1= 4 S平行 四 边 形 ABCD ，对 角 线 BD 被 EF 、 AC 、 GH 平 均 分 成 四 段， 又 OM EF ， 所 以2 3DO : ED BD :4 4 BD 2 : 3 ，OE :
16、 ED ED OD : ED 3 2 : 3 1 : 3 ，所 以 SA AEO 1 1 S3 4 平 行 四 边 形 ABCD 1 1 72 63 4( 平 方 厘 米 ) ，SA ADO 2 SA AEO 12 (平 方 厘米 )同理可 得S ACFM 6 平方 厘 米 ，SA CDM 12 平方 厘米 所以 SA ABC SAAEO SACFM 36 6 6 24 (平方 厘米 )，于是 ，阴影 部分 的面 积为 24 12 12 48 (平方厘 米 )10. 如图 ， 在三角形 ABC 中 ， CE = 2AE ，F 是A D 的中点 ， 三角形A BC 的面 积是 1， 那么 阴影部
17、分的面积是多 少 ？A3 3 E F 31 2BD C【分析 】连接CF ，根据燕 尾定 理 ，S ABF BD 1 ，S ABF AE 1 ,S ACF DC 2 S CBF EC设 S BDF 1 份 ，则S DCF 2 份 ，S ABF 3 份 ，S AEF S EFC 3 份 ，如 图所标所以S DCEF 5 5 S ABC 12 12 拓展 篇 1. 如图 ，A 、B 是两个大小 完 全一样的长方形 ， 已知这 两个长方形的长比宽 长8 厘米 ， 图 中的字母表示相应部 分的 长度 。 问 ：A 、B 中阴影部分 的周长哪个长 ？ 长多 少 ？A B【分析 】C 2(a a b) 2
18、(b 2b) 4a 4b ，C 2(a 2b a b) 4a 6b ，因 此 B 的 周 长大 ，长 了2 b ,因 为两 个长 方形 的长比 宽 长 8 厘 米 ，即( a 2b ) (a b ) 8 ，即b 8 ， 所以长 了2b 16 厘米2. 如图 ， ABCDE 是正五边形 ，CDF 是正三角形 ， BFE 等于多少度 ？【分析 】BCF 108 60 48 EDF , 因 为 BC CF , DF DE , 所 以BFC EFD 180 48 2 66 ,因此 BFE 360 66 2 60 1683. 一 个各条边分别为 5 厘米 、 12 厘米 、 13 厘米的直角三角形 ，
19、将它 的短 直角边对折到斜 边上去与斜边相重合 ， 如 图所示 。 问 ： 图中的阴影 部分 （ 即折叠的部分 ） 的 面积是多少 平方厘米 ？ADxB C【分析 】设C D x ，有 13 x (12 x) 5 ，解 得x 10 ，所以S 1 10 5 25 平方 厘米3 阴 影 2 3 34. 图中大长方形被分成四 个小长方形 ， 面 积分别为12 、 24、 36、 48。 请问 ： 图中阴影部分 的面积 是多少 ？【分析 】如图 ，阴影部分的面积等 于 1 EF CD ，所以 ，设大长方形的 长为 AB a 厘米 ，2宽为CD b 厘米 ，则有 ：EF 的长度为 ： 48 a 12 a
20、 5 a 所以 ，阴影部48 36 12 24 21分的面 积为 1 5 a b 1 5 120 100 (平 方厘 米 )2 21 2 21 75. 三个面积都是 12 的正 方形放在一个长方形 的盒 子里面 ， 如 图 ， 盒中 空白 部分的面积已 经标出 ， 求图中大长 方形 的面积 。【分 析 】将中间 的正 方形 卡片 往左 移动 ，可得 到新 的下 右图 的长方 形盒 子，S在移动 的过 程中 ，最 下方 空白部 分的 面积 没有 变动， 仍 为 3；而且 空白 部分 面积和 相等 。移动后 ，左 边和 中间 的正 方形 纸 片共 同拥 有一 个小 正方形 ，则 其各 部分 面积
21、如下图 ：3 63令面积 为3 的正 方形 的边 长为 a，则有a 2 3 ，而 面积 为6 的长方 形中 的长 为 2a，即 大的正方 方 形 纸 片 的 边 长 为 2a 。所 以 整 个 外 面 的 长 方 形 的 长 为 5a ，宽 为 3a 。所 以 其 面 积 为15a 2 45 .6. 如图 ， 三角形A BC 的面积为 1。D 、E 分别为A B 、A C 的中点 。F 、G 分别为B C 边 上的三等分点 。 请问 ： 三 角形D EF 的面积是多少 ？ 三角 形DOE 的面积是多少 ？A15aD E10aB F6a O 6a4aG10aC1【分析 】连 接 GE , DE
22、1 , DE 1 BC , FG 1 BC ,所 以 FG 3 2 ,设 S 4 a ，则BC 2 2 3 DES ADE 11 32 OFGS四 边 形 DECB 4a 6a 9a 6a 10a 10a 45a S ABC 4, 所 以 S ADE 15 a ，因 此S 60a 1 ，即a 1 ，所 以S ABC 60 DEF 15a 1 15 160 4 DOE 9a 1 9 360 207. 如图 ， 梯形A BCD 的上底A D 长 10厘米 ， 下底B C 长15 厘米 。 如果E F 与上 、 下底平行 ， 那么 EF 的长度是多少 ？【分析 】 AO 10 2 , OF 3 ,所
23、 以OF 3 10 6 厘 米 , EO 2 , EO 2 15 6 厘 米 ,因OC 15 3 AD 5 5 BC 5 5此EF 6 6 12 厘米8. 如图 ， 正六边形的面积 为 6， 那么阴影部分的面 积是多少 ？【分析 】连接 FC，根 据梯 形蝴 蝶定 理 ，面 积为 4 6 89 3A FB EC D阴 影9. 两盏 4 米高的 路灯相 距 10米 ， 有一 个身高 1.5 米的同学行走在 这两盏 路灯之间 ， 那么他的两个影子总长度 是多 少米 ？【分析 】设每人 的影 子长 为x 米 ，根 据相似 有 1.5 4 xx 5 ，解 得 x 3 ，所 以他 的两个 影子 总长度是
24、2 x 2 3 6 米10. 如 图 ， O 是长方形 ABCD 一条对角线的中 点 ， 图中 已 经标 出 两个三角形的面积为 3 和 4， 那么阴影直角三角形 的面 积是多少 ？A D EOB F C【分析 】连 接 CO , 根 据 题 意 有2S COE 4 3 1 , 所 以 DE 3OE , 即EF BE 5 , S阴 影 5 25 ,即 S 25 8 25CD BD 8 S BCD 8 64 64 811. 如图 ， 在三角形 ABC 中 ， AE ED ，D 点是 BC 的 四等分点 ， 阴 影部分的 面积占三角 形ABC 面积的几分之 几 ？A3 E F3 1B D C【分析
25、 】设S 1 ,则S S 3 ,根 据 燕 尾 模 型 有S 1 , AF S ABE 3 ,所 以 CDE BDE ABE AEC CF S BCE 47 S3 S阴 影33 7 3S AEF ,因此 ABC 3 3 1 1 712. 如图 ， 在三角形 ABC 中 ， 三角形 AEO 的面积是 1， 三角形 ABO 的面积是 2， 三角形 BOD的面积是 3， 则四边形 DCEO 的面积是多少 ？A1 E2 O3 xBD C【分析 】连接OC ,设S x ，S COD DO 3 ,所以S 2 x ，则S 2 x 1 COD S AOC AO 22 x 1 AOC 3 COE 3有 S BC
26、O S COE , 3 x 3 ，所以x 15 ，因 此S 四 边 形 DCEO 5 x 1 24S ABO S AOE 2 1 3 超 越 篇 1. 如图 ， 长方形的面积 是60 平方厘米 ， 其内3 条长 度相等且两两夹角为 120的线段将长方形分成了两个梯形 和一 个三角形 。 请问 ： 一 个梯 形的面积是多少平方 厘米 ？411【分析 】如 图， 添加 辅助 线 ，长 方形 被分 成 了12 份 。 梯形占5 份 ，所 以， 梯形面 积 =60 12 5=25（平方厘 米 ）2. 如 图 ，P 是 三 角 形 ABC 内 一 点 ，DE 平 行 于A B ，F G 平 行 于B C
27、 ，HI 平 行于 CA ， 四 边形 AIPD 的面积是 12， 四边 形P GCH 的面积是 15， 四边形B EPF 的面 积是20 。 请问 ：三角形 ABC 的面积是多少 ？【解析 】 本题主 要应 用 ：夹在 平行 线间的 平行 四边 形面 积之 比等于 底边 长度 之 比 （等 高。 由于S AIPD:S PHCG=IP:PH所以 ，IP:PH=12:15=4:5同理可 推 ，PD:PE=3:5，FP:PE=4:3连接I D，即可 利用 共角 定 理求 SPEH =12.5同理 ，可求 其余 部分 。答案 ：三角 形A BC 的 面积 是72 平方 厘米 。3. 如图所示 ， 正
28、方形 ABCD 的面积为 1。 E 、F 分别是B C 和DF 的重点 ，DE 与B F 交于M 点 ，DE 与A F 交于N 点 ， 那么阴影 三角形M FN 的面积为多少 ？A DN GM FB E C【 分析 】过F 点做F G EC则 ， FG DF 1EC DC 2又B C 2EC AD 4 FG, BE 2 FG FG 1 , FG 1AD 4 BE 2 FG / / AD / / BC FN FG 1 , FM FG 1AN AD 4 BM BE 2 SA FNM 1 1 1SA ABFSA FNM5 3 15 1 S 1 1 115 A ABF 15 2 304. 如图 ， 三
29、角形A BC 的面积为 1 ，D 、E 、F 分别是三条 边 上的三等分点 ， 求阴影三 角形的面积 。1 2答案 ： 175. 如图 ， 小悦测出家 里的 瓷砖的长为 24厘米 ， 宽 为 10厘米 ， 而且还测 出了 边上的中间线 段均为 4 厘米 ， 那么中间 菱形的面积是多少平 方厘 米 ？A Bh1M4 N h2 Q PC D4【 分析 】 连接C D则CD 24 AB : CD 4 : 24 1: 6h : h AB : CD 1: 6又h 1 h2 3 4 7(cm), h1 1(cm)MP 10 2 8(cm)同理，N Q 16(cm)S菱 形 = 1 816=64 cm2）2
30、6. 如 图 ， ED 垂 直 于 等 腰 梯 形 ABCD 的 上 底 AD ， 并 交 BC 于 G ， AE 平 行 于 BD ，DCB =45， 且三角形 ABD 和三角形E DC 的面积分别为 75、 45， 那么三角形A ED 的 面积是多少 ？EA DB G C【分析 】从A 点向B C 做 垂线 交 BC 于F 点 ，交B D 于H 点 。三角 形A BH 面 积等 于三 角 形C DE 的 面积 ，又 四边 形 AEDH 为平 行四 边形 。 所以三 角 形A ED 的 面积 =75-45=30。EA DHB F G C7. 在 长 方 形 ABCD 中 ， E 、 F 、G
31、 、H 分 别 是 边 AB 、B C 、 CD 、DA 上 的 点， 将 长 方 形 的 四 个 角 分 别 沿 着 HE 、E F 、F G 、GH 对 折 后 ，A 点 与B 点 重 合 ，C 点 与 D 点 重合 。 已知 EH =3，E F =4， 求线段A D 与 AB 的长度比 。【 分析 】A H DKE GLB F C如图可 知 ，令K 为A 与B 重合 的 点 ，L 为C 与D 重 合的点 。则 有：E 为A E 中点 ，且 等 于E K 长度 ，由于 AEH HEK , KEF BEF ,所以有 ：HEF 90 ,所以 HF=5，EK= 12 ；所以 AB 24 ，由于
32、AH BF HF 5 .所以 ：AD : AB 5 524 : 5 24 : 2558. 如图 ， 在长方形 ABCD 中 ， AE : ED AF : AB BG : GC 。 已知 EFC 的面积为 20， FGD的面积为 16， 那么长方形 ABCD 的面积是多少 ？【 分析 】 令AE a ，DE b ，AF c ，BF d ， 则有 ：a c ， 由 于b c dS三 角 形 CEF a b c d 1 ac 1 b c d 1 d a b 1 ac bc ad 20 2 2 2 2由 知 ，a c ad bc ， 代 入 得 ：b c 20 。 所 以S三 角 形 DFG a b (c d ) 1 a b c 1 ad 1 b c d 1 ac ad bd 16 2 2 2 21 bc bd 1 20 bd 16 ， 则b d 12 。2 2所以S 长 方 形 ABCD ac ad bc bd 2bc bd 40 12 52所以长 方形 的面 积 为52 。
