1、广西省梧州市 2019 年中考数学试题(解析版) 一选择题 16 的倒数是（ ）A6 B6 C D【考点】17：倒数【分析】根据倒数的定义，a 的倒数是 （a0），据此即可求解【解答】解：6 的倒数是： 故选：C2下列计算正确的是（ ）A3xx 3 B2x+3x5x 2C（2x） 24 x2 D（x+y） 2x 2+y2【考点】35：合并同类项；47：幂的乘方与积的乘方；4C：完全平方公式【分析】直接利用合并同类项法则以及积的乘方运算法则、完全平方公式分别化简得出答案【解答】解：A、3x x2x，故此选项错误；B、2x+3x5x ，故此选项错误；C、（2x） 24 x2，正确；D、（x+y）
2、2x 2+2xy+y2，故此选项错误；故选：C3一个几何体的主视图和左视图都是矩形，俯视图是圆，则这个几何体是（ ）A圆柱 B圆锥 C球 D正方体【考点】U1：简单几何体的三视图； U3：由三视图判断几何体【分析】根据几何体的主视图和左视图都是矩形，得出几何体是柱体，再根据俯视图为圆，易判断该几何体是一个圆柱【解答】解：一个几何体的主视图和左视图都是矩形，俯视图是圆，符合这个条件的几何体只有圆柱，因此这个几何体是圆柱体故选：A4下列函数中，正比例函数是（ ）Ay8x By Cy8x 2 Dy 8x 4【考点】F2：正比例函数的定义【分析】直接利用正比例函数以及反比例函数、二次函数、一次函数的定
3、义分别分析得出答案【解答】解：A、y 8x，是正比例函数，符合题意；B、y ，是反比例函数，不合题意；C、y 8x2，是二次函数，不合题意；D、y8x4，是一次函数，不合题意；故选：A5如图，钟表上 10 点整时，时针与分针所成的角是（ ）A30 B60 C90 D120【考点】IG ：钟面角【分析】根据钟面分成 12 个大格，每格的度数为 30即可解答【解答】解：钟面分成 12 个大格，每格的度数为 30，钟表上 10 点整时，时针与分针所成的角是 60故选：B6直线 y3x+1 向下平移 2 个单位，所得直线的解析式是（ ）Ay3x+3 By3x 2 Cy3x+2 Dy 3x 1【考点】F
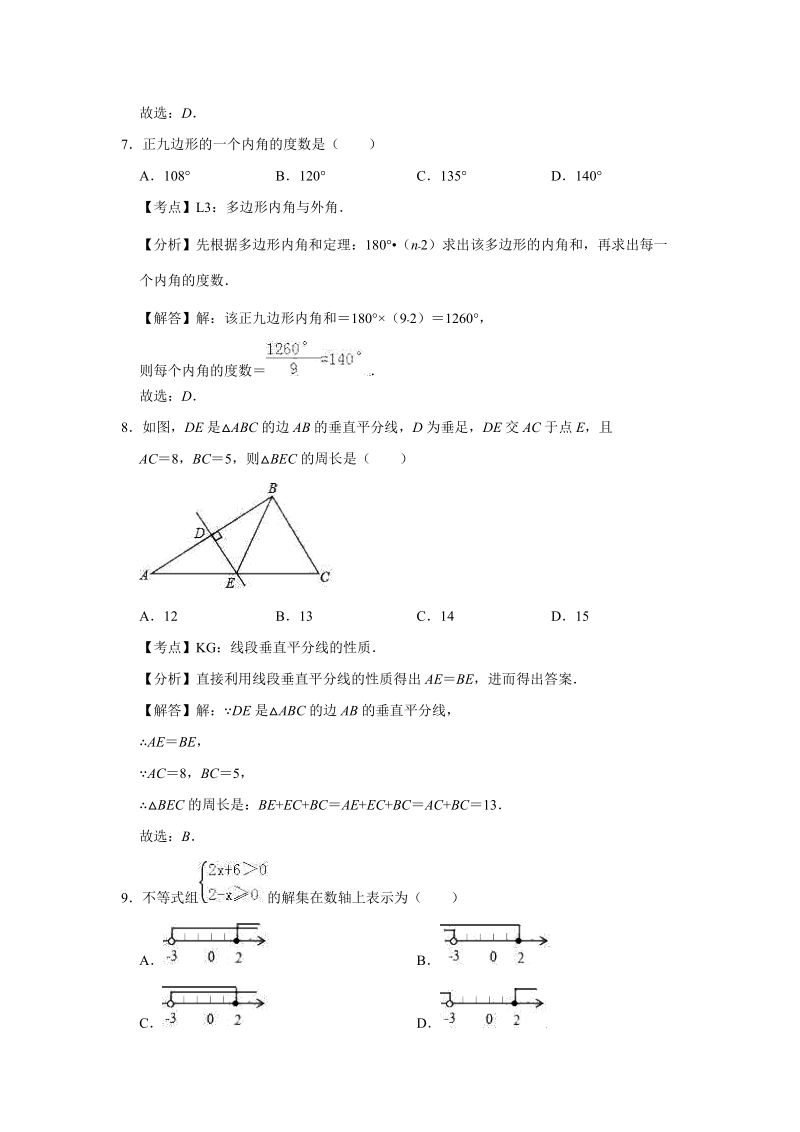
4、9：一次函数图象与几何变换【分析】直接利用一次函数平移规律进而得出答案【解答】解：直线 y3x +1 向下平移 2 个单位，所得直线的解析式是：y3x+123x 1故选：D7正九边形的一个内角的度数是（ ）A108 B120 C135 D140【考点】L3：多边形内角与外角【分析】先根据多边形内角和定理：180（n2）求出该多边形的内角和，再求出每一个内角的度数【解答】解：该正九边形内角和180（92）1260 ，则每个内角的度数 故选：D8如图，DE 是ABC 的边 AB 的垂直平分线，D 为垂足，DE 交 AC 于点 E，且AC8，BC5，则BEC 的周长是（ ）A12 B13 C14 D
5、15【考点】KG：线段垂直平分线的性质【分析】直接利用线段垂直平分线的性质得出 AEBE，进而得出答案【解答】解：DE 是ABC 的边 AB 的垂直平分线，AEBE，AC8，BC5，BEC 的周长是：BE+EC+ BCAE+EC+BC AC +BC13故选：B9不等式组 的解集在数轴上表示为（ ）A BC D【考点】C4：在数轴上表示不等式的解集； CB：解一元一次不等式组【分析】分别求出不等式组中两不等式的解集，找出解集的公共部分确定出不等式组的解集，表示在数轴上即可【解答】解： ，由得： x3；由得： x2，不等式组的解集为 3x 2，表示在数轴上，如图所示：故选：C10某校九年级模拟考试
6、中，1 班的六名学生的数学成绩如下：96，108，102，110，108，82下列关于这组数据的描述不正确的是（ ）A众数是 108 B中位数是 105C平均数是 101 D方差是 93【考点】W1：算术平均数；W4：中位数；W5 ：众数；W7 ：方差【分析】把六名学生的数学成绩从小到大排列为：82，96，102，108，108，110，求出众数、中位数、平均数和方差，即可得出结论【解答】解：把六名学生的数学成绩从小到大排列为：82，96，102，108，108，110，众数是 108，中位数为 105，平均数为 101，方差为 （82101） 2+（96101） 2+（102101） 2+（
7、108 101） 2+（108101）2+（110 101） 294.393；故选：D11如图，在半径为 的O 中，弦 AB 与 CD 交于点 E，DEB75，AB 6，AE1，则 CD 的长是（ ）A2 B2 C2 D4【考点】KQ：勾股定理；M2：垂径定理【分析】过点 O 作 OFCD 于点 F，OG AB 于 G，连接 OB、OD ，由垂径定理得出DFCF，AG BG AB3，得出 EGAGAE2，由勾股定理得出 OG2，证出EOG 是等腰直角三角形，得出OEG 45 ，OE OG2 ，求出OEF30，由直角三角形的性质得出 OF OE ，由勾股定理得出 DF ，即可得出答案【解答】解：
8、过点 O 作 OFCD 于点 F，OG AB 于 G，连接 OB、OD ，如图所示：则 DFCF，AGBG AB3，EGAGAE2，在 RtBOG 中，OG 2，EGOG，EOG 是等腰直角三角形，OEG45，OE OG2 ，DEB75，OEF30，OF OE ，在 RtODF 中，DF ，CD2DF 2 ；故选：C12已知 m0，关于 x 的一元二次方程（x+1）（x2） m0 的解为 x1，x 2（x 1x 2），则下列结论正确的是（ ）Ax 112x 2 B 1x 12x 2 C1x 1x 22 Dx 1 1x 22【考点】AA：根的判别式；AB：根与系数的关系；HA：抛物线与 x 轴的
9、交点【分析】可以将关于 x 的方程（x+1）（x 2）m0 的解为 x1，x 2 看作是二次函数m（x+1）（x 2）与 x 轴交点的横坐标，而与 x 轴交点坐标可以通过二次函数的关系式求得，即可以求出 x1 与 x2，当函数值 m0 时，就是抛物线位于 x 轴上方的部分所对应的 x 的取值范围，再根据 x1x 2，做出判断【解答】解：关于 x 的一元二次方程（x+1）（x 2）m0 的解为 x1，x 2，可以看作二次函数 m（x+1）（x 2）与 x 轴交点的横坐标，二次函数 m（ x+1）（x 2）与 x 轴交点坐标为（ 1，0），（2，0），如图：当 m0 时，就是抛物线位于 x 轴上方
10、的部分，此时 x1，或 x2；又 x1x 2x11，x 22；x112x 2，故选：A二填空题 13计算： 2 【考点】24：立方根【分析】根据立方根的定义即可求解【解答】解：2 38 2故答案为：214如图，已知在ABC 中，D、E 分别是 AB、AC 的中点， F、G 分别是 AD、AE 的中点，且 FG 2cm，则 BC 的长度是 8 cm【考点】KX：三角形中位线定理【分析】利用三角形中位线定理求得 FG DE，DE BC【解答】解：如图，ADE 中，F、G 分别是 AD、AE 的中点，DE2FG4cm，D， E 分别是 AB，AC 的中点，DE 是ABC 的中位线，BC2DE8cm
11、，故答案为：815化简： a a 4 【考点】6B：分式的加减法【分析】直接将分式的分子分解因式，进而约分得出答案【解答】解：原式 a a2a4 aa4故答案为：a4 16如图，ABCD 中， ADC119，BE DC 于点 E，DFBC 于点 F，BE 与 DF 交于点H，则 BHF 61 度【考点】L5：平行四边形的性质【分析】直接利用平行四边形的性质以及结合三角形内角和定理得出答案【解答】解：四边形 ABCD 是平行四边形，ADBC，DCAB ，ADC119，DFBC，ADF90，则EDH 29，BEDC，DEH90，DHEBHF9029 61故答案为：6117如图，已知半径为 1 的O
12、 上有三点 A、B、C，OC 与 AB 交于点 D，ADO85，CAB20 ，则阴影部分的扇形 OAC 面积是 【考点】M5：圆周角定理；MO：扇形面积的计算【分析】根据三角形外角的性质得到CADO CAB65，根据等腰三角形的性质得到AOC50，由扇形的面积公式即可得到结论【解答】解：ADO85， CAB20，CADO CAB65 ，OAOC，OACC 65，AOC50，阴影部分的扇形 OAC 面积 ，故答案为： 18如图，在菱形 ABCD 中，AB2，BAD60 ，将菱形 ABCD 绕点 A 逆时针方向旋转，对应得到菱形 AEFG，点 E 在 AC 上，EF 与 CD 交于点 P，则 DP
13、 的长是 1 【考点】KM：等边三角形的判定与性质；L8 ：菱形的性质；R2：旋转的性质【分析】连接 BD 交 AC 于 O，由菱形的性质得出 CDAB 2， BCDBAD60，ACDBAC BAD30，OAOC，AC BD，由直角三角形的性质求出OB AB1，OA OB ，得出 AC2 ，由旋转的性质得：AEAB2，EAG BAD 60 ，得出 CEACAE2 2，证出 CPE90 ，由直角三角形的性质得出 PE CE 1，PC PE3 ，即可得出结果【解答】解：连接 BD 交 AC 于 O，如图所示：四边形 ABCD 是菱形，CDAB2，BCD BAD60，ACD BAC BAD30 ，O
14、AOC，ACBD，OB AB1，OA OB ，AC2 ，由旋转的性质得：AEAB 2，EAGBAD60 ，CEACAE 2 2，四边形 AEFG 是菱形，EFAG，CEPEAG60，CEP+ACD90，CPE90 ，PE CE 1，PC PE3 ，DPCD PC2（3 ） 1；故答案为： 1三解答题 19计算：52+3 （ 1）【考点】1G：有理数的混合运算【分析】直接利用有理数的混合运算法则计算得出答案【解答】解：原式10+1+18 20先化简，再求值： ，其中 a 2【考点】6D：分式的化简求值【分析】直接利用幂的乘方运算法则以及同底数幂的乘除运算法则分别化简得出答案【解答】解：原式 a
15、22a2a 2，当 a2 时，原式 421解方程： +1 【考点】B3：解分式方程【分析】直接利用分式方程的解法解方程得出答案【解答】解：方程两边同乘以（x 2）得：x 2+2+x26，则 x2+x60，（x2）（x+3）0，解得：x 12，x 23，检验：当 x2 时，x 20，故 x2 不是方程的根，x3 是分式方程的解22一个不透明的口袋中有三个完全相同的小球，球上分别标有数字1，1，2第一次从袋中任意摸出一个小球（不放回），得到的数字作为点 M 的横坐标 x；再从袋中余下的两个小球中任意摸出一个小球，得到的数字作为点 M 的纵坐标 y（1）用列表法或树状图法，列出点 M（x，y）的所有
16、可能结果；（2）求点 M（x，y）在双曲线 y 上的概率【考点】G6：反比例函数图象上点的坐标特征； X6：列表法与树状图法【分析】根据摸秋规则，可借助树状图表示所有的情况数，然后再根据坐标，找出坐标满足 y 的点的个数，由概率公式可求【解答】解：（1）用树状图表示为：点 M（x，y）的所有可能结果；（1，1）（ 1，2）（1，1）（1，2）（2， 1）（2，1）共六种情况（2）在点 M 的六种情况中，只有（ 1，2）（2，1）两种在双曲线 y 上，P ；因此，点 M（x，y）在双曲线 y 上的概率为 23如图，在 RtABC 中，C90 ，D 为 BC 上一点，AB 5，BD1，tanB （
17、1）求 AD 的长；（2）求 sin 的值【考点】T7：解直角三角形【分析】（1）根据 tanB ，可设 AC3x，得 BC4x，再由勾股定理列出 x 的方程求得 x，进而由勾股定理求 AD；（2）过点 D 作 DEAB 于点 E，解直角三角形求得 BE 与 DE，进而求得结果【解答】解：（1）tanB ，可设 AC3x，得 BC4x，AC2+BC2AB 2，（ 3x） 2+（4x） 25 2，解得，x1（舍去），或 x1，AC3，BC4，BD1，CD3，AD ；（2）过点作 DEAB 于点 E，tanB ，可设 DE3y，则 BE4y，AE2+DE2BD 2，（ 3y） 2+（4y） 21
18、2，解得，y （舍），或 y ， ，sin 24我市某超市销售一种文具，进价为 5 元/件售价为 6 元/ 件时，当天的销售量为 100件在销售过程中发现：售价每上涨 0.5 元，当天的销售量就减少 5 件设当天销售单价统一为 x 元/ 件（x 6，且 x 是按 0.5 元的倍数上涨），当天销售利润为 y 元（1）求 y 与 x 的函数关系式（不要求写出自变量的取值范围）；（2）要使当天销售利润不低于 240 元，求当天销售单价所在的范围；（3）若每件文具的利润不超过 80%，要想当天获得利润最大，每件文具售价为多少元？并求出最大利润【考点】AD：一元二次方程的应用；HE：二次函数的应用【分析
19、】（1）根据总利润每件利润销售量，列出函数关系式，（2）由（1）的关系式，即 y240，结合二次函数的性质即可求 x 的取值范围（3）由题意可知，利润不超过 80%即为利润率（售价进价）售价，即可求得售价的范围再结合二次函数的性质，即可求【解答】解：由题意（1）y（x5）（100 5）10x 2+210x800故 y 与 x 的函数关系式为：y10x 2+210x800（2）要使当天利润不低于 240 元，则 y240，y10x 2+210x80010（x 10.5） 2+302.5240解得，x 18，x 213100 ，抛物线的开口向下，当天销售单价所在的范围为 8x13（3）每件文具利润
20、不超过 80% ，得 x9文具的销售单价为 6x9，由（1）得 y10x 2+210x800 10（x10.5） 2+302.5对称轴为 x10.56x9 在对称轴的左侧，且 y 随着 x 的增大而增大当 x9 时，取得最大值，此时 y 10（910.5） 2+302.5280即每件文具售价为 9 元时，最大利润为 280 元25如图，在矩形 ABCD 中，AB4，BC3，AF 平分DAC，分别交 DC，BC 的延长线于点 E， F；连接 DF，过点 A 作 AHDF，分别交 BD，BF 于点 G，H（1）求 DE 的长；（2）求证：1 DFC【考点】KD：全等三角形的判定与性质；LB ：矩形
21、的性质；S9：相似三角形的判定与性质【分析】（1）由 ADCF，AF 平分DAC，可得FAC AFC，得出 ACCF 5，可证出ADEFCE，则 ，可求出 DE 长；（2）由ADGHBG，可求出 DG，则 ，可得 EGBC，则 1AHC，根据DFAH，可得 AHC DFC，结论得证【解答】（1）解：矩形 ABCD 中，ADCF ，DAFACF，AF 平分DAC ，DAFCAF，FACAFC，ACCF，AB4，BC3， 5，CF5，ADCF，ADEFCE， ，设 DEx，则 ，解得 x ；（2）AD FH，AF DH，四边形 ADFH 是平行四边形，ADFH3，CH2，BH 5，ADBH，ADG
22、HBG， ， ，DG ，DE ， ，EGBC，1AHC，又 DFAH，AHCDFC，1 DFC26如图，已知A 的圆心为点（3，0），抛物线 yax 2 x+c 过点 A，与A 交于B、C 两点，连接 AB、AC ，且 ABAC，B、C 两点的纵坐标分别是 2、1（1）请直接写出点 B 的坐标，并求 a、c 的值；（2）直线 ykx+1 经过点 B，与 x 轴交于点 D点 E（与点 D 不重合）在该直线上，且 ADAE，请判断点 E 是否在此抛物线上，并说明理由；（3）如果直线 yk 1x1 与A 相切，请直接写出满足此条件的直线解析式【考点】HF：二次函数综合题【分析】（1）证明 RtBRA
23、RtASC（AAS），即可求解；（2）点 E 在直线 BD 上，则设 E 的坐标为（x， x+1），由 ADAE，即可求解；（3）分当切点在 x 轴下方、切点在 x 轴上方两种情况，分别求解即可【解答】解：（1）过点 B、C 分别作 x 轴的垂线交于点 R、S，BAR+RAB90，RAB+CAS 90，RABCAR，又 ABAC ，RtBRARtASC（AAS ），ASBR2，AR CS 1，故点 B、C 的坐标分别为（2 ，2）、（5，1），将点 B、C 坐标代入抛物线 yax 2 x+c 并解得：a ，c11，故抛物线的表达式为：y x2 x+11；（2）将点 B 坐标代入 ykx+1 并
24、解得：y x+1，则点 D（2，0），点 A、B、C 、D 的坐标分别为（3，0）、（2，2）、（5，1）、（2，0），则 AB ，AD5，点 E 在直线 BD 上，则设 E 的坐标为（x， x+1），ADAE，则 52（3x） 2+（ x+1） 2，解得：x2 或 6（舍去2），故点 E（6，4），把 x6 代入 y x2 x+114，故点 E 在抛物线上；（3） 当切点在 x 轴下方时，设直线 yk 1x1 与A 相切于点 H，直线与 x 轴、y 轴分别交于点 K、G （0， 1），连接GA，AHAB ，GA ，AHKKOG90，HKA HKA， KOGKHA， ，即： ，解得：KO2 或 （舍去 ），故点 K（2，0 ），把点 K、G 坐标代入 yk 1x1 并解得：直线的表达式为：y x1；当切点在 x 轴上方时，直线的表达式为：y2x 1；故满足条件的直线解析式为：y x1 或 y2x 1
