1、2018 年黑龙江省哈尔滨市阿城区中考数学二模试卷一、选择题1 （3 分）2018 的绝对值是（ ）A2018 B2018 C D20182 （3 分）下列运算正确的是（ ）Aa 3a2a 6 B （x 3） 3x 6 Cx 5+x5x 10 Da 8a4a 43 （3 分）下列四个图形中既是轴对称图形，又是中心对称图形的是（ ）A B C D4 （3 分）下面的几何体中，主视图为三角形的是（ ）A BC D5 （3 分）已知反比例函数 y 的图象位于第一、第三象限，则 k 的取值范围是（ ）Ak8 Bk8 Ck8 Dk 86 （3
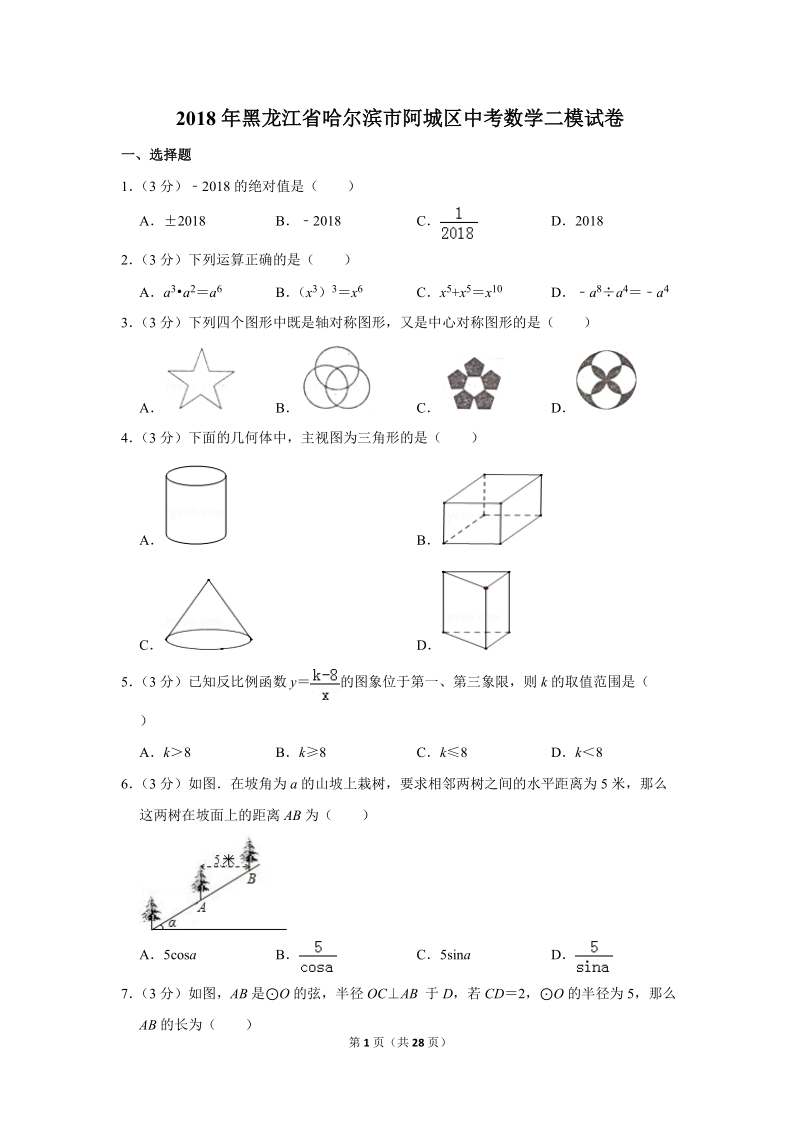
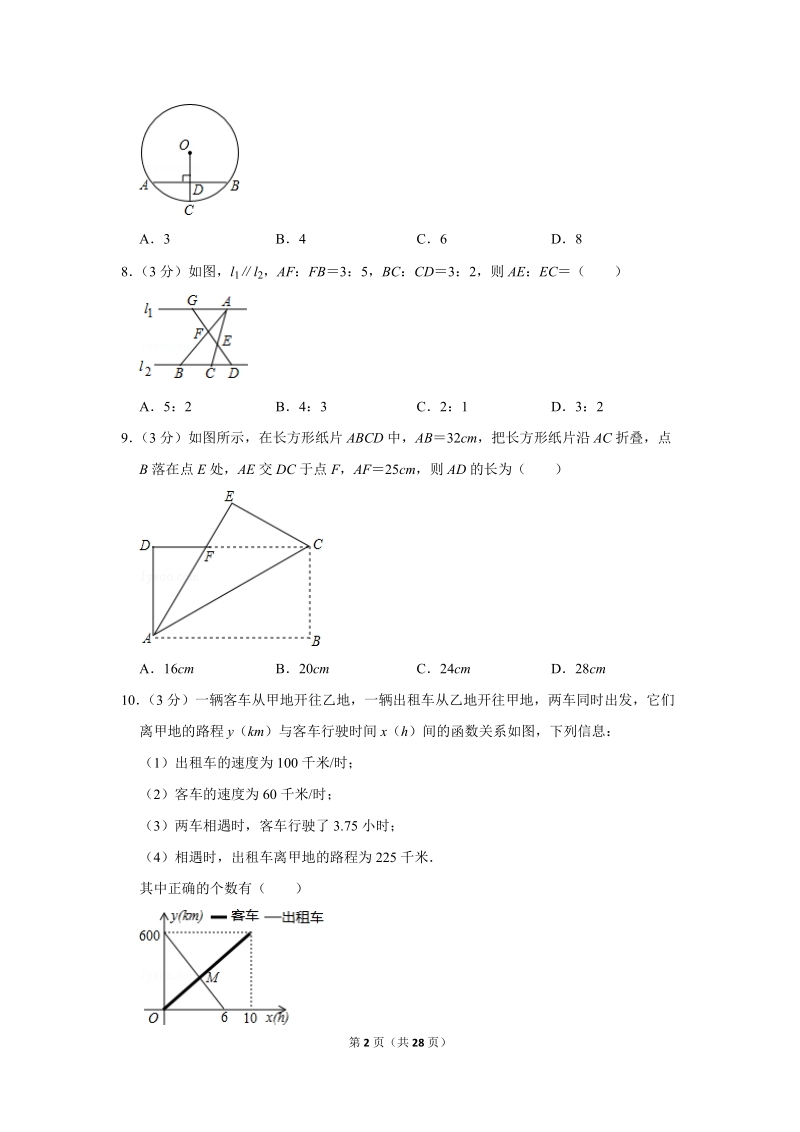
2、分）如图在坡角为 a 的山坡上栽树，要求相邻两树之间的水平距离为 5 米，那么这两树在坡面上的距离 AB 为（ ）A5cosa B C5sina D7 （3 分）如图，AB 是O 的弦，半径 OCAB 于 D，若 CD2，O 的半径为 5，那么AB 的长为（ ）第 2 页（共 28 页）A3 B4 C6 D88 （3 分）如图，l 1l 2，AF：FB3：5，BC ：CD3： 2，则 AE：EC（ ）A5：2 B4：3 C2：1 D3：29 （3 分）如图所示，在长方形纸片 ABCD 中，AB32cm ，把长方形纸片沿 AC 折叠，点B 落在点 E 处，
3、AE 交 DC 于点 F，AF 25cm ，则 AD 的长为（ ）A16cm B20cm C24cm D28cm10 （3 分）一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，它们离甲地的路程 y（km ）与客车行驶时间 x（h）间的函数关系如图，下列信息：（1）出租车的速度为 100 千米/时；（2）客车的速度为 60 千米/时；（3）两车相遇时，客车行驶了 3.75 小时；（4）相遇时，出租车离甲地的路程为 225 千米其中正确的个数有（ ）第 3 页（共 28 页）A1 个 B2 个 C3 个 D4 个二、填空题11 （3 分）某风扇在网上累计销量
4、约 1570000 台，请将 1570000 用科学记数法表示为 12 （3 分）函数 y 中自变量 x 的取值范围是 13 （3 分）计算： （ ） 14 （3 分）因式分解：4ax 24ay 2 15 （3 分）不等式组 的整数解是 16 （3 分）一个扇形的面积是 cm，半径是 3cm，则此扇形的弧长是 17 （3 分）若将抛物线 y4（x+2） 23 图象向左平移 5 个单位，再向上平移 3 个单位得到的抛物
5、线的顶点坐标是 18 （3 分）在一个不透明的口袋中，有 3 个红球、2 个黄球、一个白球，它们除颜色不同之外其它完全相同，现从口袋中随机摸出一个球记下颜色后放回，再随机摸出一个球，则两次摸到一个红球和一个黄球的概率是 19 （3 分）菱形 ABCD 中，A60，AB9，点 P 是菱形 ABCD 内一点，PBPD 3，则 AP 的长为 20 （3 分）如图，在四边形 ABCD 中，AC、BD 是对角线，ACAD，BCAB ，ABCD，AB4，BD2 ， tanBAC3 ，则线段 BC 的长是 &nb
6、sp; 三、解答题21 （7 分）先化简，再求值：1+ （1 ） ，其中 x2cos30+tan4522 （7 分）如图，是 55 正方形网格，每个小正方形的边长为 1，请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上第 4 页（共 28 页）（1）在图（1）中画出一个等腰ABE，使其面积为 3.5；（2）在图（2）中画出一个直角CDF，使其面积为 5，并直接写出 DF 的长23 （8 分）如图是根据对某区初中三个年级学生课外阅读的“漫画丛书” 、 “科普常识” 、“名人传记” 、 “其它”中，最喜欢阅读的一种读物进行随机抽样调查，并绘制了下面不完整的条形统计图和
7、扇形统计图（每人必选一种读物，并且只能选一种） ，根据提供的信息，解答下列问题：（1）求该区抽样调查人数；（2）补全条形统计图，并求出最喜欢“其它”读物的人数在扇形统计图中所占的圆心角度数；（3）若该区有初中生 14400 人，估计该区有初中生最喜欢读“名人传记”的学生是多少人？24 （8 分）如图，已知点 A、C 在四边形对角线 EF 上，ADBC，DEBF，AECF（1）求证：四边形 ABCD 是平行四边形；（2）直接写出 4 对图中相等的线段（AECF 除外） 25 （10 分）某地一路段修建，甲队单独完成这项工程需要 60 天，若由甲队先做 5 天，再第 5 页（共 28 页）由甲、乙
8、两队合作 9 天，共完成这项工程的三分之一（1）求甲、乙两队合作完成这项工程需要多少天？（2）若甲队的工作效率提高 20%，乙队工作效率提高 50%，甲队施工 1 天需付工程款4 万元，乙队施工一天需付工程款 2.5 万元，现由甲乙两队合作若干天后，再由乙队完成剩余部分，在完成此项工程的工程款不超过 190 万元的条件下要求尽早完成此项工程，则甲、乙两队至多要合作多少天？26 （10 分）如图，AB 是 O 的直径，弧 CDAB，垂足为 H，P 为弧 AD 上一点，连接PA、 PB，PB 交 CD 于 E（1）如图（1）连接 PC、CB，求证：BCPPED；（2）如图（2）过点 P 作O 的切
9、线交 CD 的延长线于点 E，过点 A 向 PF 引垂线，垂足为 G，求证：APG F；（3）如图（3）在图（2）的条件下，连接 PH，若 PH PF，3PF5PG，BE2 ，求 O 的直径 AB27 （10 分）如图，在平面直角坐标系中，抛物线 yx 22ax 与 x 轴相交于 O、A 两点，OA4，点 D 为抛物线的顶点，并且直线 ykx+b 与该抛物线相交于 A、B 两点，与 y轴相交于点 C，B 点的横坐标是1（1）求 k，a，b 的值；（2）若 P 是直线 AB 上方抛物线上的一点，设 P 点的横坐标是 t，PAB 的面积是 S，求 S 关于 t 的函数关系式，并直接写出自变量 t
10、的取值范围；（3）在（2）的条件下，当 PBCD 时，点 Q 是直线 AB 上一点，若BPQ+CBO180，求 Q 点坐标第 6 页（共 28 页）第 7 页（共 28 页）2018 年黑龙江省哈尔滨市阿城区中考数学二模试卷参考答案与试题解析一、选择题1 （3 分）2018 的绝对值是（ ）A2018 B2018 C D2018【分析】根据绝对值的定义即可求得【解答】解：2018 的绝对值是 2018，故选：D【点评】本题主要考查的是绝对值的定义，熟练掌握相关知识是解题的关键2 （3 分）下列运算正确的是（ ）Aa 3a2a 6 B （x 3） 3x 6 Cx 5+x5
11、x 10 Da 8a4a 4【分析】各项计算得到结果，即可作出判断【解答】解：A、原式a 5，不符合题意；B、原式x 9，不符合题意；C、原式2x 5，不符合题意；D、原式a 4，符合题意，故选：D【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键3 （3 分）下列四个图形中既是轴对称图形，又是中心对称图形的是（ ）A B C D【分析】根据轴对称图形与中心对称图形的概念求解【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、是轴对称图形，也是中心对称图形
12、，故此选项正确故选：D【点评】此题主要考查了中心对称图形与轴对称图形的概念轴对称图形的关键是寻找第 8 页（共 28 页）对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部分重合4 （3 分）下面的几何体中，主视图为三角形的是（ ）A BC D【分析】主视图是从几何体的正面看所得到的图形，根据主视图所看的方向，写出每个图形的主视图及可选出答案【解答】解：A、主视图是长方形，故 A 选项错误；B、主视图是长方形，故 B 选项错误；C、主视图是三角形，故 C 选项正确；D、主视图是正方形，中间还有一条线，故 D 选项错误；故选：C【点评】此题主要考查了
13、简单几何体的三视图，关键是掌握主视图所看的位置5 （3 分）已知反比例函数 y 的图象位于第一、第三象限，则 k 的取值范围是（ ）Ak8 Bk8 Ck8 Dk 8【分析】本题考查反比例函数的图象和性质，由 k80 即可解得答案【解答】解：反比例函数 y 的图象位于第一、第三象限，k80，解得 k8，故选：A【点评】本题考查了反比例函数的图象和性质：、当 k0 时，图象分别位于第一、三象限；当 k0 时，图象分别位于第二、四象限、当 k0 时，在同一个象限内，y 随 x 的增大而减小；当 k 0 时，在同一个象限，y 随 x 的增大而增大第 9 页（共 28 页）6 （3 分）如图
14、在坡角为 a 的山坡上栽树，要求相邻两树之间的水平距离为 5 米，那么这两树在坡面上的距离 AB 为（ ）A5cosa B C5sina D【分析】运用余弦函数求两树在坡面上的距离 AB 即可【解答】解：由于相邻两树之间的水平距离为 5 米，坡角为 ，则两树在坡面上的距离 AB 故选：B【点评】此题主要考查了坡度坡角问题，正确掌握三角函数关系是解题关键7 （3 分）如图，AB 是O 的弦，半径 OCAB 于 D，若 CD2，O 的半径为 5，那么AB 的长为（ ）A3 B4 C6 D8【分析】连接 OA，构建直角三角形 AOD；利用垂径定理求得 AB2AD；然后在直角
15、三角形 AOD 中由勾股定理求得 AD 的长度，从而求得 AB2AD8【解答】解：连接 OA O 的半径为 5，CD2，OD523，即 OD3；又AB 是O 的弦，OCAB，AD AB；第 10 页（共 28 页）在直角三角形 ODC 中，根据勾股定理，得AD 4，AB8故选：D【点评】本题考查了垂径定理、勾股定理解答该题的关键是通过作辅助线 OA 构建直角三角形，在直角三角形中利用勾股定理求相关线段的长度8 （3 分）如图，l 1l 2，AF：FB3：5，BC ：CD3： 2，则 AE：EC（ ）A5：2 B4：3 C2：1 D3：2【分析】依据平行线分线段成比例定理，即可得到A
16、G3x ，BD5x ，CD BD2x，再根据平行线分线段成比例定理，即可得出 AE 与EC 的比值【解答】解：l 1l 2， ，设 AG3x，BD5x ，BC：CD3：2，CD BD2x，AGCD， 故选：D【点评】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例9 （3 分）如图所示，在长方形纸片 ABCD 中，AB32cm ，把长方形纸片沿 AC 折叠，点B 落在点 E 处， AE 交 DC 于点 F，AF 25cm ，则 AD 的长为（ ）第
17、11 页（共 28 页）A16cm B20cm C24cm D28cm【分析】首先根据平行线的性质以及折叠的性质证明EACDCA，根据等角对等边证明 FCAF，则 DF 即可求得，然后在直角ADF 中利用勾股定理求解【解答】解：长方形 ABCD 中，ABCD，BACDCA，又BACEAC，EACDCA，FCAF25 cm，又长方形 ABCD 中，DCAB32cm，DFDCFC32257cm，在直角ADF 中，AD 24（ cm） 故选：C【点评】本题考查了折叠的性质以及勾股定理，在折叠的过程中注意到相等的角以及相等的线段是关键10 （3 分）一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两
18、车同时出发，它们离甲地的路程 y（km ）与客车行驶时间 x（h）间的函数关系如图，下列信息：（1）出租车的速度为 100 千米/时；（2）客车的速度为 60 千米/时；（3）两车相遇时，客车行驶了 3.75 小时；（4）相遇时，出租车离甲地的路程为 225 千米其中正确的个数有（ ）第 12 页（共 28 页）A1 个 B2 个 C3 个 D4 个【分析】根据题意和函数图象中的数据可以判断各个小题是否正确，从而可以解答本题【解答】解：由图象可得，出租车的速度为：6006100 千米/时，故（1）正确，客车的速度为：6001060 千米/时，故（2）正确，两车相遇时，客车行驶时间为
19、：600（100+60）3.75（小时） ，故（3）正确，相遇时，出租车离甲地的路程为：603.75225 千米，故（4）正确，故选：D【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答二、填空题11 （3 分）某风扇在网上累计销量约 1570000 台，请将 1570000 用科学记数法表示为 1.57106 【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：将
20、1570000 用科学记数法表示为 1.57106故答案为：1.5710 6【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n 的形式，其中 1|a| 10 ，n 为整数，表示时关键要正确确定 a 的值以及 n 的值12 （3 分）函数 y 中自变量 x 的取值范围是 x 【分析】根据被开方数是非负数且分母不能为零，可得答案【解答】解：由题意，得3x+20，第 13 页（共 28 页）解得x ，故答案为：x 【点评】本题考查了函数自变量的取值范围，利用被开方数是非负数且分母不能为零得出不等式是解题关键13 （3 分）计算： （ ） 【分析】先根据二
21、次根式的乘法法则运算，然后化简后合并即可【解答】解：原式 2 3 故答案为 【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍14 （3 分）因式分解：4ax 24ay 2 4a（x y） （x+y） 【分析】首先提取公因式 4a，再利用平方差公式分解因式即可【解答】解：4ax 24ay 24a（x 2y 2）4a（xy） （x +y） 故答案为：4a（xy ） （x +y） 【点评】此题主要考查了提取公因式法以及公式法分解因式
22、，正确运用公式是解题关键15 （3 分）不等式组 的整数解是 3、4 【分析】分别解出两个不等式的解集，再表示出其公共部分即可【解答】解：解不等式 x10，得：x3，解不等式 x1613x ，得：x ，则不等式组的解集为 3x ，第 14 页（共 28 页）所以不等式组的整数解为 3、4，故答案为：3、4【点评】本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断还可以观察不等式的解，若 x较小的数、较大的数，那么解集为 x 介于两数之间16 （3 分）一个扇形的面积是 cm，半径是 3cm，则此扇形的弧长是 【分析】设此扇形的弧长为 l，根据扇形面积公式计算即可【解
23、答】解：设此扇形的弧长为 l，S lr， l3，解得，l ，故答案为： 【点评】本题考查的是扇形面积公式，掌握扇形面积公式 S lr 是解题的关键17 （3 分）若将抛物线 y4（x+2） 23 图象向左平移 5 个单位，再向上平移 3 个单位得到的抛物线的顶点坐标是 （7，0） 【分析】直接利用平移规律“左加右减，上加下减”得出平移后的解析式进而得出答案【解答】解：将抛物线 y4（x+2） 23 图象向左平移 5 个单位，再向上平移 3 个单位，平移后的解析式为：y4（x+7） 2，故得到的抛物线的顶点坐标是：（7，0） 故答案为：（7，0） 【点评】此题主要考查了二次函数与几何变换，正确掌
24、握平移规律是解题关键18 （3 分）在一个不透明的口袋中，有 3 个红球、2 个黄球、一个白球，它们除颜色不同之外其它完全相同，现从口袋中随机摸出一个球记下颜色后放回，再随机摸出一个球，则两次摸到一个红球和一个黄球的概率是 【分析】先画树状图展示所有 36 种等可能的结果数，再找出两次摸到一个红球和一个黄球的结果数，然后根据概率公式求解第 15 页（共 28 页）【解答】解：画树状图如下：由树状图可知，共有 36 种等可能结果，其中两次摸到一个红球和一个黄球的结果数为12，所以两次摸到一个红球和一个黄球的概率为 ，故答案为：【点评】本题考查了列表法或树状图法：通过列表
25、法或树状图法展示所有等可能的结果求出 n，再从中选出符合事件 A 或 B 的结果数目 m，然后根据概率公式求出事件 A 或 B的概率19 （3 分）菱形 ABCD 中，A60，AB9，点 P 是菱形 ABCD 内一点，PBPD 3，则 AP 的长为 3 或 6 【分析】分成 P 在 OA 上和 P 在 OC 上两种情况进行讨论，根据ABD 是等边三角形，即可求得 OA 的长度，在直角 OBP 中利用勾股定理求得 OP 的长，则 AP 即可求得【解答】解：设 AC 和 BE 相交于点 O当 P 在 OA 上时，ABAD ，A60，ABD 是等边三角形，BDAB9，OBO
26、D BD 则 AO 在直角OBP 中，OP 则 APOA OP 3 ；当 P 在 OC 上时，APOA +OP 6 第 16 页（共 28 页）故答案是：3 或 6 【点评】本题考查了菱形的性质，注意到 P 在 AC 上，应分两种情况进行讨论是解题的关键20 （3 分）如图，在四边形 ABCD 中，AC、BD 是对角线，ACAD，BCAB ，ABCD，AB4，BD2 ， tanBAC3 ，则线段 BC 的长是 6 【分析】作 DEAB ，交 BA 的延长线于 E，作 CFAB，可得 DECF ，且 ACAD，可证 RtADERtAFC，可得 AEAF，DAEBAC，根据 tanBACDAE3
27、，可设 DE3 a，AEa，根据勾股定理可求 a 的值，由此可得 BF，CF 的值再根据勾股定理求 BC 的长【解答】解：如图：作 DEAB，交 BA 的延长线于 E，作 CFAB，ABCD，DEAB ，CFABCFDE，且 ACADRtADERtAFCAEAF，DAE BACtanBAC 3tanDAE3设 AEa，DE3 a在 Rt BDE 中，BD 2DE 2+BE2第 17 页（共 28 页）52（4+a）2+27 a2解得 a11，a 2 （不合题意舍去）AE1AF，DE3 CFBFABAF3在 Rt BFC 中，BC【点评】本题是解直角三角形问题，恰当地构建辅助线是本题的关键，利用
28、三角形全等证明边相等，并借助同角的三角函数值求线段的长，与勾股定理相结合，依次求出各边的长即可三、解答题21 （7 分）先化简，再求值：1+ （1 ） ，其中 x2cos30+tan45【分析】先化简分式，再计算 x 的值，最后把 x 的值代入化简后的分式，计算出结果【解答】解：原式1+ 1+ 1+当 x2cos30 +tan452 +1 +1 时原式【点评】本题主要考查了分式的加减及锐角三角函数值解决本题的关键是掌握分式的运算法则和运算顺序22 （7 分）如图，是 55 正方形网格，每个小正方形的边长为 1，请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上第 18 页（共 2
29、8 页）（1）在图（1）中画出一个等腰ABE，使其面积为 3.5；（2）在图（2）中画出一个直角CDF，使其面积为 5，并直接写出 DF 的长【分析】 （1）直接利用等腰三角形的定义结合勾股定理得出答案；（2）利用直角三角的定义结合勾股定理得出符合题意的答案【解答】解：（1）如图（1）所示：ABE，即为所求；（2）如图（2）所示：CDF 即为所求，DF 【点评】此题主要考查了等腰三角形的定义以及三角形面积求法，正确应用网格分析是解题关键23 （8 分）如图是根据对某区初中三个年级学生课外阅读的“漫画丛书” 、 “科普常识” 、“名人传记” 、 “其它”中，最喜欢阅读的一种读物进行随机抽样调查，
30、并绘制了下面不完整的条形统计图和扇形统计图（每人必选一种读物，并且只能选一种） ，根据提供的信息，解答下列问题：（1）求该区抽样调查人数；（2）补全条形统计图，并求出最喜欢“其它”读物的人数在扇形统计图中所占的圆心角度数；（3）若该区有初中生 14400 人，估计该区有初中生最喜欢读“名人传记”的学生是多少人？第 19 页（共 28 页）【分析】 （1）由“科普知识”人数及其百分比可得总人数；（2）总人数乘以“漫画丛书”的人数求得其人数即可补全图形，用 360乘以“其他”人数所占比例可得；（3）总人数乘以“名人传记”的百分比可得【解答】解：（1）84035%2400（人） ，该区抽样调查的人数
31、是 2400 人；（2）240025%600（人） ，该区抽样调查最喜欢“漫画丛书”的人数是 600 人，补全图形如下：36021.6，最喜欢“其它”读物的人数在扇形统计图中所占的圆心角是度数 21.6；（3）从样本估计总体：1440034%4896（人） ，答：估计最喜欢读“名人传记”的学生是 4896 人【点评】本题考查的是条形统计图和扇形统计图的综合运用读懂统计图，从统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图能够清楚地表示各部分所占的百分比24 （8 分）如图，已知点 A、C 在四边形对角线 EF 上，ADBC，DEBF，AECF第 20 页
32、（共 28 页）（1）求证：四边形 ABCD 是平行四边形；（2）直接写出 4 对图中相等的线段（AECF 除外） 【分析】 （1）证ADECBF，得 ADCB，从而得出四边形 ABCD 是平行四边形；（2）由全等三角形的性质和平行四边形的性质容易得出结果【解答】 （1）证明：AD BC，DEBF，BEDDFB，DACBCA，DAEBCF，在ADE 和CBF 中， ，ADECBF（ASA） ，ADCB，四边形 ABCD 是平行四边形；（2）ADBC、ECAF 、ED BF 、ABDC、BEDF ；理由如下：ADECBF，ADBC，EDBF ，AECF，ECAF，四边形 ABCD 是平行四边形，
33、ABDC【点评】本题考查了平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，并能进行推理论证是解决问题的关键25 （10 分）某地一路段修建，甲队单独完成这项工程需要 60 天，若由甲队先做 5 天，再由甲、乙两队合作 9 天，共完成这项工程的三分之一（1）求甲、乙两队合作完成这项工程需要多少天？（2）若甲队的工作效率提高 20%，乙队工作效率提高 50%，甲队施工 1 天需付工程款4 万元，乙队施工一天需付工程款 2.5 万元，现由甲乙两队合作若干天后，再由乙队完第 21 页（共 28 页）成剩余部分，在完成此项工程的工程款不超过 190 万元的条件下要求尽早完成此项工程，
34、则甲、乙两队至多要合作多少天？【分析】 （1）设甲、乙两队合作完成这项工程需要 x 天，根据条件：甲队先做 5 天，再由甲、乙合作 9 天，共完成总工作量的 ，列方程求解即可；（2）设甲、乙两队最多合作元天，先求出甲、乙两队合作一天完成工程的多少，再根据完成此项工程的工程款不超过 190 万元，列出不等式，求解即可得出答案【解答】解：（1）设甲、乙两队合作完成这项工程需要 x 天根据题意得， ，解得 x36，经检验 x36 是分式方程的解，答：甲、乙两队合作完成这项工程需要 36 天，（2）甲队的工作效率提高 20%，乙队工作效率提高 50%，甲队的工单独工作 50 天，乙队单独工作 60 天
35、，设甲、乙需要合作 y 天，根据题意得，190，解得 y40.答：甲、乙两队至多要合作 40 天【点评】本题考查了分式方程的应用和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解，注意检验26 （10 分）如图，AB 是 O 的直径，弧 CDAB，垂足为 H，P 为弧 AD 上一点，连接PA、 PB，PB 交 CD 于 E（1）如图（1）连接 PC、CB，求证：BCPPED；（2）如图（2）过点 P 作O 的切线交 CD 的延长线于点 E，过点 A 向 PF 引垂线，垂足为 G，求证：APG F；（3）如图（3）在图（2）的条件下，连接 PH，若 PH
36、 PF，3PF5PG，BE2 ，第 22 页（共 28 页）求 O 的直径 AB【分析】 （1）由垂径定理得出CPBBCD，根据BCPBCD+PCD CPB+PCDPED 即可得证；（2）连接 OP，知 OPOB ，先证FPEFEP 得F+2FPE180，再由APG+FPE90 得 2APG+2FPE180，据此可得 2APGF，据此即可得证；（3）连接 AE，取 AE 中点 N，连接 HN、PN ，过点 E 作 EMPF，先证PAEF，由 tanPAEtanF 得 ，再证GAP MPE ，由 sinGAPsinMPE 得 ，从而得出 ，即 MFGP，由 3PF5PG 即 可设 PG3k，得P
37、F5k、MF PG3k 、PM2k，由FPEPEF 知 PFEF5k、EM4k 及PE2 k、AP k，证PEMABP 得 BP3 k，继而可得BE k2，据此求得 k 2，从而得出 AP、BP 的长，利用勾股定理可得答案【解答】证明：（1）AB 是 O 的直径且 ABCD，CPBBCD，BCPBCD+PCD CPB+PCDPED，BCPPED；（2）连接 OP，则 OPOB ，OPBOBP，第 23 页（共 28 页）PF 是O 的切线，OPPF，则OPF90，FPE 90OPE，PEF HEB90OBP，FPE FEP，AB 是O 的直径，APB 90，APG+FPE90，2APG+2FP
38、E180，F+FPE +PEF180 ，F+2FPE 1802APGF ，APG F ；（3）连接 AE，取 AE 中点 N，连接 HN、PN ，过点 E 作 EMPF 于 M，由（2）知APBAHE90，ANEN，A、H、E 、P 四点共圆，PAE PHF，PHPF，PHFF，PAE F，tanPAEtanF ， ，第 24 页（共 28 页）由（2）知APBGPME90，GAPMPE，sinGAP sinMPE，则 ， ，MFGP ，3PF5PG ， ，设 PG3k，则 PF5k ，MFPG 3k，PM 2k由（2）知FPEPEF ，PFEF5k ，则 EM4k，tanPEM ，tan F
39、 ，tanPAE ，PE 2 k，AP k，APG+EPMEPM + PEM90，APGPEM，APG+OPA ABP +BAP90，且OAPOPA，APGABP，PEM ABP，则 tanABPtanPEM，即 ， ，则 BP3 k，BE k2 ，则 k2，第 25 页（共 28 页）AP3 、BP 6 ，根据勾股定理得，AB15【点评】本题主要考查圆的综合问题，解题的关键是掌握圆周角定理、四点共圆条件、相似三角形的判定与性质、三角函数的应用等知识点27 （10 分）如图，在平面直角坐标系中，抛物线 yx 22ax 与 x 轴相交于 O、A 两点，OA4，点 D 为抛物线的顶点，并且直线 y
40、kx+b 与该抛物线相交于 A、B 两点，与 y轴相交于点 C，B 点的横坐标是1（1）求 k，a，b 的值；（2）若 P 是直线 AB 上方抛物线上的一点，设 P 点的横坐标是 t，PAB 的面积是 S，求 S 关于 t 的函数关系式，并直接写出自变量 t 的取值范围；（3）在（2）的条件下，当 PBCD 时，点 Q 是直线 AB 上一点，若BPQ+CBO180，求 Q 点坐标【分析】 （1）根据题意可得 A（4，0）代入抛物线解析式可得 a，求出抛物线解析式，根据 B 的横坐标可求 B 点坐标，把 A，B 坐标代入直线解析式，可求 k，b（2）过 P 点作 PNOA 于 N，交 AB 于
41、M，过 B 点作 BHPN ，设出 P 点坐标，可求出 N 点坐标，即可以用 t 表示 S（3）由 PBCD，可求 P 点坐标，连接 OP，交 AC 于点 R，过 P 点作 PNOA 于 M，交 AB 于 N，过 D 点作 DTOA 于 T，根据 P 的坐标，可得POA45，由 OAOC可得CAO45则 POAB，根据抛物线的对称性可知 R 在对称轴上设 Q 点坐标，根据BORPQS ，可求 Q 点坐标【解答】解：（1）OA4A（4，0）16+8a0第 26 页（共 28 页）a2，yx 24x ，当 x1 时，y1+43，B（1，3） ，将 A（4，0）B（1，3）代入函数解析式，得，解得直
42、线 AB 的解析式为 yx +4，k1、a2、b4；（2）过 P 点作 PNOA 于 N，交 AB 于 M，过 B 点作 BHPN ，如图 1，由（1）知直线 AB 是 yx +4，抛物线是 yx 24x，当 xt 时， yPt 24t， yNt+4PNt 24t（t+4）t 25t 4，BH1t，AM t（4）t+4，SPAB PN（ AM+BH） （t 25t4） （1t +t+4） （t 25t 4）3，化简，得 s t2 t6，自变量 t 的取值范围是4t1；4t1（3）yx 24x ，当 x2 时，y4 即 D（2，4） ，当 x0 时，yx+44，即C（0，4） ，CDOAB（1，
43、3） 当 y3 时，x3，P（3，3） ，连接 OP，交 AC 于点 R，过 P 点作 PNOA 于 M，交 AB 于 N，过 D 点作 DTOA 于T，如图 2，可证 R 在 DT 上PNON3第 27 页（共 28 页）PONOPN45BPR PON45，OAOC，AOC90PBR BAO45，POACBPQ+CBO180，BPQBCO+BOC过点 Q 作 QSPN，垂足是 S，SPQBORtanSPQtanBOR，可求 BR ，OR 2 ，设 Q 点的横坐标是 m，当 xm 时 ym+4，SQm+3，PSm1 ，解得 m 当 x 时，y ，Q（ ， ） 【点评】本题考查二次函数综合题、一次函数的应用、相似三角形的判定和性质、全等第 28 页（共 28 页）三角形的判定和性质等知识，解题的关键是灵活运用所学知识，学会添加常用辅助线，构造特殊四边形解决问题，属于中考压轴题
