1、2018 年辽宁省丹东市宽甸县中考数学二模试卷一、选择题（下列各题的备选答案中，只有一个是正确的，每小题 3 分，共 24 分)1 （3 分）下列说法正确的是（ ）A|2|2 B0 的倒数是 0C4 的平方根是 2 D3 的相反数是 32 （3 分）将 0.000 102 用科学记数法表示为（ ）A1.0210 4 B1.02I 05 C1.0210 6 D10210 33 （3 分）下列计算正确的是（ ）A3a2aa B2a3a6a Ca 2a3a 6 D （3a） 26a 24 （3 分）如图所示的几何体的主视图是（ ）A BC D5 （3
2、分）平面直角坐标系中，点 P（2，3）关于 x 轴对称的点的坐标为（ ）A （2，3） B （2，3） C （3，2） D （3，2）6 （3 分）下列判定正确的是（ ）A对角线互相垂直的四边形是菱形B四边相等且有一个角是直角的四边形是正方形C两角相等的四边形是梯形D两条对角线相等且互相垂直的四边形是正方形7 （3 分）甲、乙两人同时分别从 A，B 两地沿同一条公路骑自行车到 C 地已知 A，C 两地间的距离为 110 千米，B，C 两地间的距离为 100 千米甲骑自行车的平均速度比乙快 2 千米/时结果两人同时到达 C 地求两人的平均速度，为解决此问题，设乙骑自行车的
3、平均速度为 x 千米/时由题意列出方程其中正确的是（ ）第 2 页（共 30 页）A B C D 8 （3 分）如图，已知点 A 是双曲线 y 在第二象限分支的一个动点，连结 AO 并延长交另一分支于点 B，以 AB 为边作等边三角形 ABC，点 C 在第一象限内，且随着点 A的运动，点 C 的位置也在不断变化，但点 C 始终在双曲线 y 上运动，则 k 的值是（ ）A3 B3 C3 D3二、填空题(每小题 3 分,共 24 分)9 （3 分）函数 中，自变量 x 的取值范围是 10 （3 分）分解因式：a 3ab 2 &nbs
4、p; 11 （3 分）甲、乙、丙、丁四名射击运动员分别连续射靶 10 次，他们各自的平均成绩及其方差如表所示，如果选一名成绩好且发挥稳定的运动员参赛，则应选择的运动员是 甲 乙 丙 丁平均成绩（环） 8.6 8.4 8.6 7.6方差 0.94 0.74 0.56 1.9212 （3 分）如图，将长方形 ABCD 沿 AE 折叠，使点 D 落在 BC 边上的点 F，若BFA34，则DAE 度13 （3 分）抛物线 yax 2+bx+c（a0）经过点（2，5） ， （4，5） ，则对称轴是 第 3 页（共 30
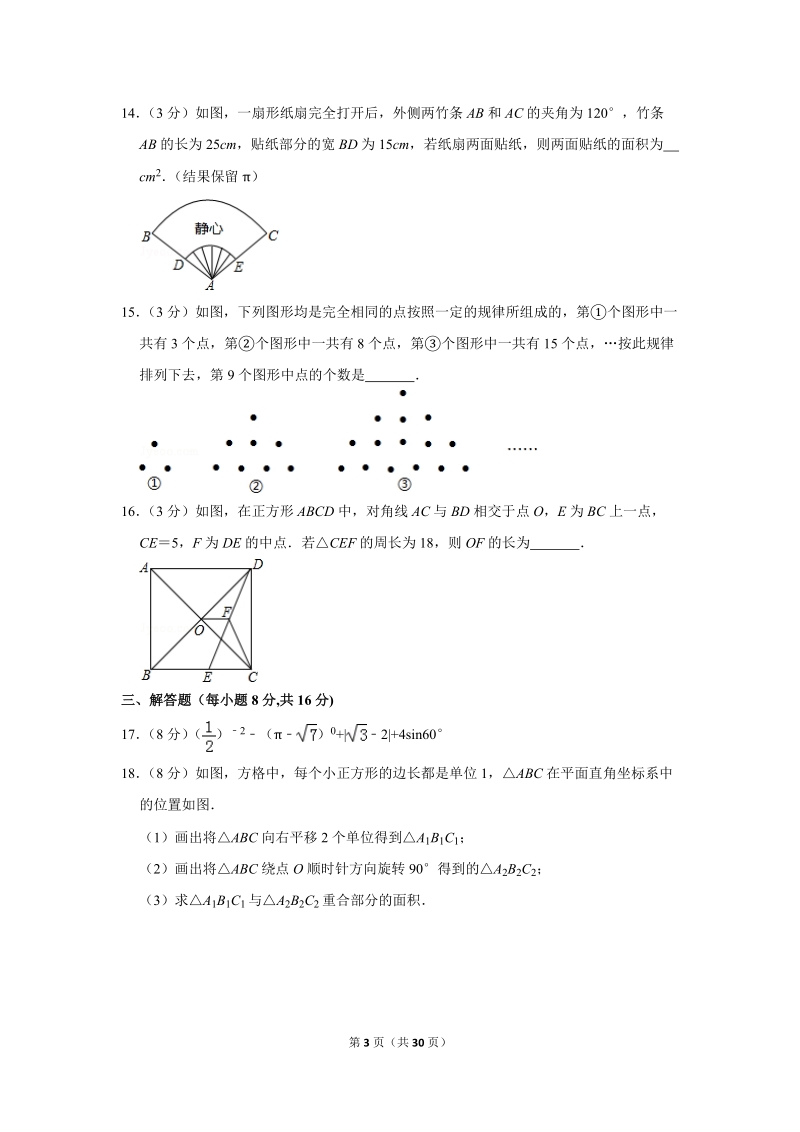
5、页）14 （3 分）如图，一扇形纸扇完全打开后，外侧两竹条 AB 和 AC 的夹角为 120，竹条AB 的长为 25cm，贴纸部分的宽 BD 为 15cm，若纸扇两面贴纸，则两面贴纸的面积为 cm2 （结果保留 ）15 （3 分）如图，下列图形均是完全相同的点按照一定的规律所组成的，第个图形中一共有 3 个点，第个图形中一共有 8 个点，第 个图形中一共有 15 个点，按此规律排列下去，第 9 个图形中点的个数是 16 （3 分）如图，在正方形 ABCD 中，对角线 AC 与 BD 相交于点 O，E 为 BC 上一点，CE5，F 为 DE
6、 的中点若CEF 的周长为 18，则 OF 的长为 三、解答题（每小题 8 分,共 16 分)17 （8 分） （ ） 2 （ ） 0+| 2|+4sin60 18 （8 分）如图，方格中，每个小正方形的边长都是单位 1，ABC 在平面直角坐标系中的位置如图（1）画出将ABC 向右平移 2 个单位得到A 1B1C1；（2）画出将ABC 绕点 O 顺时针方向旋转 90得到的A 2B2C2；（3）求A 1B1C1 与A 2B2C2 重合部分的面积第 4 页（共 30 页）四、解答题（每小题 10 分，共 20 分）19 （10 分）某校的春季趣味运动会深受学生喜爱，该校
7、体育教师为了了解该次运动会中四个项目的受欢迎程度，随机抽取了部分学生进行问卷调查，被调查学生须从“托球跑、掷飞盘、推小车、鸭子步”四个项目中选择自己最喜欢的一项根据调查结果，体育教师绘制了图 1 和图 2 两个统计图（均未完成） ，请根据图 1 和图 2 的信息，解答下列问题（1）此次共调查了多少名学生？（2）将条形统计图补充完整（3）图 2 中“鸭子步”所在扇形圆心角为多少度？（4）若全校有学生 1600 人，估计该校喜欢“推小车”项目的学生人数20 （10 分）一个有进水管与出水管的容器，从某时刻开始 4min 内只进水不出水，在随后的 8min 内既进水又出水，每分的进水量和出水量有两个
8、常数，容器内的水量 y（单位：L）与时间 x（单位：min）之间的关系如图所示（1）当 4x12 时，求 y 关于 x 的函数解析式；（2）直接写出每分进水，出水各多少升第 5 页（共 30 页）五、(每小题 10 分,共 20 分)21 （10 分）若 n 是一个两位正整数，且 n 的个位数字大于十位数字，则称 n 为“两位递增数” （如 13，35，56 等） 在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6 构成的所有的“两位递增数”中随机抽取 1 个数，且只能抽取一次（1）写出所有个位数字是 5 的“两位递增数” ；（2）请用列表法或树状图，求抽取的“两位递增数”的个位
9、数字与十位数字之积能被10 整除的概率22 （10 分）如图，RtABC 中，ACB90，以 BC 为直径的O 交 AB 于点D，E、 F 是 O 上两点，连接 AE、CF 、DF，满足 EACA（1）求证：AE 是O 的切线；（2）若O 的半径为 3，tanCFD ，求 AD 的长六、(每小题 10 分,共 20 分)23 （10 分）如图，AB 是长为 10m，倾斜角为 37的自动扶梯，平台 BD 与大楼 CE 垂直，且与扶梯 AB 的长度相等，在 B 处测得大楼顶部 C 的仰角为 65，求大楼 CE 的高度（结果保留整数） （参考数据：sin37 ，tan37 ，sin65 ， tan6
10、5 ）第 6 页（共 30 页）24 （10 分）近年来雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注某单位计划在室内安装空气净化装置，需购进 A、B 两种设备每台 B 种设备价格比每台 A 种设备价格多 0.7 万元，花 3 万元购买 A 种设备和花 7.2 万元购买 B 种设备的数量相同（1）求 A 种、B 种设备每台各多少万元？（2）根据单位实际情况，需购进 A、B 两种设备共 20 台，总费用不高于 15 万元，求A 种设备至少要购买多少台？七、(本题 12 分)25 （12 分）如图，已知正方形 ABCD 的边长为 4，点 P 是 AB 边上的一个动点，连接CP，过点 P
11、 作 PC 的垂线交 AD 于点 E，以 PE 为边作正方形 PEFG，顶点 G 在线段 PC上对角线 EG、FP 相交于点 O（1）若 AP3，求 AE 的长；（2）连接 AC，判断点 O 是否在 AC 上，并说明理由；（3）在点 P 从点 A 到点 B 的运动过程中，正方形 PEFG 也随之运动，求 DE 的最小值八、 （本题 14 分）26 （14 分）如图，顶点为 M 的抛物线 ya（x+1） 24 分别与 x 轴相交于点 A，B（点 A在点 B 的右侧） ，与 y 轴相交于点 C（0，3） 第 7 页（共 30 页）（1）求抛物线的函数表达式；（2）判断BCM 是否为直角三角形，并说
12、明理由（3）抛物线上是否存在点 N（点 N 与点 M 不重合） ，使得以点 A，B，C ，N 为顶点的四边形的面积与四边形 ABMC 的面积相等？若存在，求出点 N 的坐标；若不存在，请说明理由第 8 页（共 30 页）2018 年辽宁省丹东市宽甸县中考数学二模试卷参考答案与试题解析一、选择题（下列各题的备选答案中，只有一个是正确的，每小题 3 分，共 24 分)1 （3 分）下列说法正确的是（ ）A|2|2 B0 的倒数是 0C4 的平方根是 2 D3 的相反数是 3【分析】利用绝对值的代数意义，倒数的定义，平方根及相反数的定义判断即可【解答】解：A、|2|2，错误；B、0 没有
13、倒数，错误；C、4 的平方根为2，错误；D、3 的相反数为 3，正确，故选：D【点评】此题考查了平方根，相反数，绝对值以及倒数，熟练掌握各自的定义是解本题的关键2 （3 分）将 0.000 102 用科学记数法表示为（ ）A1.0210 4 B1.02I 05 C1.0210 6 D10210 3【分析】绝对值小于 1 的负数也可以利用科学记数法表示，一般形式为 a10n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的 0 的个数所决定【解答】解：0.000 1021.0210 4 故选：A【点评】此题主要考查了用科学记数法表示较小的数
14、，一般形式为 a10n ，其中1|a| 10，n 为由原数左边起第一个不为零的数字前面的 0 的个数所决定3 （3 分）下列计算正确的是（ ）A3a2aa B2a3a6a Ca 2a3a 6 D （3a） 26a 2【分析】根据合并同类项，单项式乘以单项式，同底数幂的乘法，积的乘方，即可解答【解答】解：A、正确；第 9 页（共 30 页）B、2a3a6a 2，故错误；C、a 2a3a 5，故错误；D、 （3a） 29a 2，故错误；故选：A【点评】本题考查了合并同类项，单项式乘以单项式，同底数幂的乘法，积的乘方，解决本题的关键是熟记合并同类项，单项式乘以单项式，同底数幂的乘法，积的
15、乘方的法则4 （3 分）如图所示的几何体的主视图是（ ）A BC D【分析】找到从正面看所得到的图形即可【解答】解：从正面看可得到左边只有 1 个，中间是 2 个正方形，右边也是 1 个正方形，故选 A【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图，解答时学生易将三种视图混淆而错误的选其它选项5 （3 分）平面直角坐标系中，点 P（2，3）关于 x 轴对称的点的坐标为（ ）A （2，3） B （2，3） C （3，2） D （3，2）【分析】直接利用关于 x 轴对称点的性质，横坐标不变，纵坐标互为相反数，进而得出答案【解答】解：点 P（2，3）关于 x
16、 轴对称的点的坐标为（2，3） 故选：A【点评】此题主要考查了关于 x 轴对称点的性质，正确记忆横纵坐标的关系是解题关键6 （3 分）下列判定正确的是（ ）第 10 页（共 30 页）A对角线互相垂直的四边形是菱形B四边相等且有一个角是直角的四边形是正方形C两角相等的四边形是梯形D两条对角线相等且互相垂直的四边形是正方形【分析】根据对角线互相垂直的平行四边形是菱形，即可判断 A；根据菱形和平行四边形的判定得出四边形既是平行四边形，又是菱形，根据正方形的判定即可 B；根据等腰梯形的判定即可判断 C；要判断一个四边形是菱形或矩形或正方形首先应是平行四边形，即对角线互相平分，根据以上内容
17、即可判断 D【解答】解：A、对角线互相垂直的平行四边形是菱形，故本选项错误；B、根据四边相等得出四边形是菱形，根据有一个角是直角得出四边形又是矩形，即四边形是正方形，故本选项正确；C、在同一底式两角相等的梯形是等腰梯形，故本选项错误；D、两条对角线平分、垂直、相等的四边形才是正方形，故本选项错误；故选：B【点评】本题考查了等腰梯形、平行四边形、菱形、矩形、正方形的判定的应用，主要考查学生运用定理进行辨析的能力，题型不错，但是一道比较容易出错的题目7 （3 分）甲、乙两人同时分别从 A，B 两地沿同一条公路骑自行车到 C 地已知 A，C 两地间的距离为 110 千米，B，C 两地间的距离为 10
18、0 千米甲骑自行车的平均速度比乙快 2 千米/时结果两人同时到达 C 地求两人的平均速度，为解决此问题，设乙骑自行车的平均速度为 x 千米/时由题意列出方程其中正确的是（ ）A B C D 【分析】设乙骑自行车的平均速度为 x 千米/ 时，则甲骑自行车的平均速度为（x+2）千米/时，根据题意可得等量关系：甲骑 110 千米所用时间乙骑 100 千米所用时间，根据等量关系可列出方程即可【解答】解：设乙骑自行车的平均速度为 x 千米/ 时，由题意得： ，故选：A【点评】此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，找出题目第 11 页（共 30 页）中的等量关系，列出方程
19、8 （3 分）如图，已知点 A 是双曲线 y 在第二象限分支的一个动点，连结 AO 并延长交另一分支于点 B，以 AB 为边作等边三角形 ABC，点 C 在第一象限内，且随着点 A的运动，点 C 的位置也在不断变化，但点 C 始终在双曲线 y 上运动，则 k 的值是（ ）A3 B3 C3 D3【分析】设点 A 的坐标为（a， ） ，连接 OC，则 OCAB，表示出 OC，过点 C作 CDx 轴于点 D，设出点 C 坐标，在 RtOCD 中，利用勾股定理可得出 x2 的值，继而得出 y 与 x 的函数关系式【解答】解：设 A（a， ） ，则 B（a， ）点 A 与点 B 关于原点对称
20、，OAOB ，ABC 为等边三角形，ABOC，OC AO，AO ，CO AO ，过点 C 作 CD x 轴于点 D，则可得BOD OCD（都是COD 的余角） ，设点 C 的坐标为（x ，y） ，则 tanBODtanOCD，即 ，第 12 页（共 30 页）解得：y x，在 Rt COD 中，CD 2+OD2OC 2，即 y2+x23a 2+ ，将 y x 代入，可得：x 2 ，故 x ，y a，则 kxy3 ，故选：D【点评】本题考查了反比例函数的综合题，涉及了解直角三角形、等边三角形的性质及勾股定理的知识，综合考察的知识点较多，解答本题的关键是将所学知识融会贯通，注意培养自己解答综合题的
21、能力二、填空题(每小题 3 分,共 24 分)9 （3 分）函数 中，自变量 x 的取值范围是 【分析】根据二次根式的意义，被开方数是非负数即可解答【解答】解：根据题意得：23x0，解得 x 故答案为：x 【点评】本题考查了函数自变量取值范围的求法要使得本题函数式子有意义，必须满足被开方数非负10 （3 分）分解因式：a 3ab 2 a（a+b） （ab） 【分析】首先提取公因式 a，进而利用平方差公式分解因式得出答案【解答】解：a 3ab 2第 13 页（共 30 页）a（a 2b 2）a（a+b） （ab） 故答案为：a（a+b） （ab） 【点评】此题主要考查了
22、提取公因式法以及公式法分解因式，熟练应用平方差公式是解题关键11 （3 分）甲、乙、丙、丁四名射击运动员分别连续射靶 10 次，他们各自的平均成绩及其方差如表所示，如果选一名成绩好且发挥稳定的运动员参赛，则应选择的运动员是 丙 甲 乙 丙 丁平均成绩（环） 8.6 8.4 8.6 7.6方差 0.94 0.74 0.56 1.92【分析】首先比较平均数，平均数相同时选择方差较小的运动员参加即可【解答】解： ，从甲和丙中选择一人参加比赛，S 甲 2S 丙 2选择丙参赛，故答案为：丙【点评】本题考查了方差的意义方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数
23、据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定12 （3 分）如图，将长方形 ABCD 沿 AE 折叠，使点 D 落在 BC 边上的点 F，若BFA34，则DAE 17 度【分析】首先根据平行线的性质得到DAF 的度数，再根据对折的知识即可求出DAE的度数【解答】解：四边形 ABCD 是矩形，ADBC第 14 页（共 30 页）BFA DAF，BFA 34，DAF34，AFE 是ADE 沿直线 AE 对折得到，DAEFAE，DAE DAF 17，故答案为 17【点评】本题主要考查了平行线的性质，解题的关键是根据平行线的性质求出DAF 的度数，
24、此题难度不大13 （3 分）抛物线 yax 2+bx+c（a0）经过点（2，5） ， （4，5） ，则对称轴是 直线 x3 【分析】根据经过的两点的纵坐标相等可得两点关于对称轴对称，然后列式求解即可得到对称轴解析式【解答】解：点（2，5） ， （4，5）纵坐标相等，对称轴为直线 x 3故答案为：直线 x3【点评】本题考查了二次函数的性质，根据纵坐标判断出两点关于对称轴对称是解题的关键14 （3 分）如图，一扇形纸扇完全打开后，外侧两竹条 AB 和 AC 的夹角为 120，竹条AB 的长为 25cm，贴纸部分的宽 BD 为 15cm，若纸扇两面贴纸，则两面贴纸的面积为 350 cm 2 （结果保
25、留 ）【分析】贴纸部分的面积等于扇形 ABC 减去小扇形 ADE 的面积，已知圆心角的度数为120，扇形的半径为 25cm 和 251510cm，可根据扇形的面积公式求出贴纸的面积【解答】解：设 ABR ，ADr，第 15 页（共 30 页）则 S 贴纸 R2 r2 （R 2r 2） （R+r） （ Rr） （25+10）（2510）175（cm 2） ，故两面贴纸的面积为：350cm 2故答案为：350【点评】本题主要考查扇形面积的计算的应用，解答本题的关键是熟练掌握扇形面积计算公式，此题难度一般15 （3 分）如图，下列图形均是完全相同的点按照一定的规律所组成的，第个图形中一共有 3 个点
26、，第个图形中一共有 8 个点，第 个图形中一共有 15 个点，按此规律排列下去，第 9 个图形中点的个数是 99 【分析】根据图形的变化规律，可得第 n 个图形中的点数一共有 2n+（2n1）+（2n3）+3+1 ，据此即可得到第 9 个图形中点的个数【解答】解：第个图形中一共有 3 个点，32+1 ，第个图形中一共有 8 个点，84+3+1，第个图形中一共有 15 个点，156+5+3+1，按此规律排列下去，第 n 个图形中的点数一共有 2n+（2n1）+（2n3）+3+1 ，当 n9 时，2n+（2n1）+（2n3）+ +118+17+15+13+3+118+18+8199，即第 9 个图
27、形中点的个数是 99 个，故答案为：99【点评】本题主要考查了图形变化类问题，解决问题的关键是依据图形的变化，得到第n 个图形中的点数一共有 2n+（2n1）+（2n3）+ +3+1第 16 页（共 30 页）16 （3 分）如图，在正方形 ABCD 中，对角线 AC 与 BD 相交于点 O，E 为 BC 上一点，CE5，F 为 DE 的中点若CEF 的周长为 18，则 OF 的长为 【分析】先根据直角三角形的性质求出 DE 的长，再由勾股定理得出 CD 的长，进而可得出 BE 的长，由三角形中位线定理即可得出结论【解答】解：CE5，CEF 的周长为 18，CF+EF
28、18513F 为 DE 的中点，DFEFBCD90，CF DE，EFCF DE6.5，DE2EF13，CD 12四边形 ABCD 是正方形，BCCD12，O 为 BD 的中点，OF 是BDE 的中位线，OF （BCCE） （125） 故答案为： 【点评】本题考查的是正方形的性质，涉及到直角三角形的性质、三角形中位线定理等知识，难度适中三、解答题（每小题 8 分,共 16 分)17 （8 分） （ ） 2 （ ） 0+| 2|+4sin60 【分析】直接利用负指数幂的性质以及零指数幂的性质和绝对值的性质、特殊角的三角第 17 页（共 30 页）函数值分别化简得出答案【解答】解：原式41+2 +2
29、5+ 【点评】此题主要考查了实数运算，正确化简各数是解题关键18 （8 分）如图，方格中，每个小正方形的边长都是单位 1，ABC 在平面直角坐标系中的位置如图（1）画出将ABC 向右平移 2 个单位得到A 1B1C1；（2）画出将ABC 绕点 O 顺时针方向旋转 90得到的A 2B2C2；（3）求A 1B1C1 与A 2B2C2 重合部分的面积【分析】 （1）将ABC 向右平移 2 个单位即可得到A 1B1C1（2）将ABC 绕点 O 顺时针方向旋转 90即可得到的A 2B2C2（3）B 2C2 与 A1B1 相交于点 E，B 2A2 与 A1B1 相交于点 F，如图，求出直线A1B1，B 2
30、C2，A 2B2，列出方程组求出点 E、F 坐标即可解决问题【解答】解：（1）如图，A 1B1C1 为所作；（2）如图，A 2B2C2 为所作；（3）B 2C2 与 A1B1 相交于点 E，B 2A2 与 A1B1 相交于点 F，如图，B 2（0，1） ，C 2（2，3） ，B 1（1，0） ，A 1（2，5） ，A 2（5，0） ，第 18 页（共 30 页）直线 A1B1 为 y5x 5，直线 B2C2 为 yx+1，直线 A2B2 为 y x+1，由 解得 ，点 E（ ， ） ，由 解得 ，点 F（ ， ） B 2F ，EF S BEF B2FEF A 1B1C1 与A 2B2C2 重合
31、部分的面积为 【点评】本题考查了作图旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形四、解答题（每小题 10 分，共 20 分）19 （10 分）某校的春季趣味运动会深受学生喜爱，该校体育教师为了了解该次运动会中四个项目的受欢迎程度，随机抽取了部分学生进行问卷调查，被调查学生须从“托球跑、掷飞盘、推小车、鸭子步”四个项目中选择自己最喜欢的一项根据调查结果，体育教师绘制了图 1 和图 2 两个统计图（均未完成） ，请根据图 1 和图 2 的信息，解答下列问题（1）此次共调查了多少名
32、学生？（2）将条形统计图补充完整第 19 页（共 30 页）（3）图 2 中“鸭子步”所在扇形圆心角为多少度？（4）若全校有学生 1600 人，估计该校喜欢“推小车”项目的学生人数【分析】 （1）根据托球跑的人数及其百分比可得总人数；（2）先用总人数乘以掷飞盘的百分比求得其人数，再用总人数减去其它项目人数求得鸭子步的人数，据此补全图形即可得；（3）用 360乘以鸭子步人数所占比例即可得；（4）总人数乘以样本中推小车人数所占比例可得【解答】解：（1）由图 1 知有 40 人选择托球跑，由图 2 知选择托球跑的人数占抽样人数的 20%，所以被调查的学生人数为 4020%200；（2）掷飞盘的人数为
33、 20035%70 人，鸭子步的人数为 200（40+70+60）30 人，补全图形如下：（3） “鸭子步”所在扇形圆心角为 360 54；（4）1600 480（人） 答：该校喜欢“推小车”项目的学生人数约 480 人【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小20 （10 分）一个有进水管与出水管的容器，从某时刻开始 4min 内只进水不出水，在随后第 20 页（共 30 页）的 8min 内既进水又出水，每分的进水量和出水量有两个常数，容器内
34、的水量 y（单位：L）与时间 x（单位：min）之间的关系如图所示（1）当 4x12 时，求 y 关于 x 的函数解析式；（2）直接写出每分进水，出水各多少升【分析】 （1）用待定系数法求对应的函数关系式；（2）每分钟的进水量根据前 4 分钟的图象求出，出水量根据后 8 分钟的水量变化求解【解答】解：（1）设当 4x12 时的直线方程为：ykx +b（k0） 图象过（4，20） 、 （12，30） ， ，解得： ，y x+15 （ 4x 12） ；（2）根据图象，每分钟进水 2045 升，设每分钟出水 m 升，则 588m 3020，解得：m 故每分钟进水、出水各是 5 升、 升【点评】此题考
35、查了一次函数的应用，解题时首先正确理解题意，然后根据题意利用待定系数法确定函数的解析式，接着利用函数的性质即可解决问题五、(每小题 10 分,共 20 分)21 （10 分）若 n 是一个两位正整数，且 n 的个位数字大于十位数字，则称 n 为“两位递增数” （如 13，35，56 等） 在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6 构成的所有的“两位递增数”中随机抽取 1 个数，且只能抽取一次第 21 页（共 30 页）（1）写出所有个位数字是 5 的“两位递增数” ；（2）请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10 整除的概率【分析】 （
36、1）根据“两位递增数”定义可得；（2）画树状图列出所有“两位递增数” ，找到个位数字与十位数字之积能被 10 整除的结果数，根据概率公式求解可得【解答】解：（1）根据题意所有个位数字是 5 的“两位递增数”是 15、25、35、45 这4 个；（2）画树状图为：共有 15 种等可能的结果数，其中个位数字与十位数字之积能被 10 整除的结果数为 3，所以个位数字与十位数字之积能被 10 整除的概率 【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件 A 或 B 的结果数目 m，然后利用概率公式计算事件 A 或事件 B的概率22 （10 分）如图，R
37、tABC 中，ACB90，以 BC 为直径的O 交 AB 于点D，E、 F 是 O 上两点，连接 AE、CF 、DF，满足 EACA（1）求证：AE 是O 的切线；（2）若O 的半径为 3，tanCFD ，求 AD 的长【分析】 （1）连接 OA，OE，易证AOCAOE（SSS） ，从而可知OEAACB90，所以 AE 是O 的切线第 22 页（共 30 页）（2）连接 CD，因为CBA CFD，所以 tanCBA tanCFD ，从而可求出AC8，利用勾股定理即可求出 AB10，再证明ADCACB，从而可求出 AD 的长度【解答】解：（1）连接 OA， OE，在AOC 与AOE 中，AOCA
38、OE（SSS）OEAACB90，OEAE，AE 是O 的切线（2）连接 CDCBACFDtanCBA tanCFD ，在 RtACB 中，tanCBA AC8由勾股定理可知：AB10，BC 为O 的直径，CDBADC90，ADCACB，DACCAB ，ADCACB ，AD6.4第 23 页（共 30 页）【点评】本题考查圆的综合问题，涉及全等三角形的性质与判定，相似三角形的性质与判定，勾股定理，圆周角定理等知识，综合程度较高，属于中等题型六、(每小题 10 分,共 20 分)23 （10 分）如图，AB 是长为 10m，倾斜角为 37的自动扶梯，平台 BD 与大楼 CE 垂直，且与扶梯 AB
39、的长度相等，在 B 处测得大楼顶部 C 的仰角为 65，求大楼 CE 的高度（结果保留整数） （参考数据：sin37 ，tan37 ，sin65 ， tan65 ）【分析】过 B 作 BFAE，利用三个角为直角的四边形为矩形得到四边形 BDEF 为矩形，由矩形的对边相等得到 DE BF，在直角三角形 ABF 中，利用锐角三角函数定义求出BF 的长，即为 DE 的长，在直角三角形 CBD 中，利用锐角三角函数定义求出 CD 的长，由 CD+DE 求出 CE 的长即可【解答】解：过 B 作 BFAE ，可得BFEBDE DEF90，四边形 BFED 为矩形，DEBF，在 Rt ABF 中，BAF3
40、7，AB10m，BF10sin37 6m，即 DE6m ，由题意得：BDAB 10m，第 24 页（共 30 页）在 Rt BCD 中， CD10tan65 m，则 CEDE+ CD +627m【点评】此题考查了解直角三角形的应用仰角俯角问题，熟练掌握锐角三角函数定义是解本题的关键24 （10 分）近年来雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注某单位计划在室内安装空气净化装置，需购进 A、B 两种设备每台 B 种设备价格比每台 A 种设备价格多 0.7 万元，花 3 万元购买 A 种设备和花 7.2 万元购买 B 种设备的数量相同（1）求 A 种、B 种设备每台各多少万元？（
41、2）根据单位实际情况，需购进 A、B 两种设备共 20 台，总费用不高于 15 万元，求A 种设备至少要购买多少台？【分析】 （1）设每台 A 种设备 x 万元，则每台 B 种设备（x+0.7）万元，根据数量总价单价结合花 3 万元购买 A 种设备和花 7.2 万元购买 B 种设备的数量相同，即可得出关于 x 的分式方程，解之并检验后即可得出结论；（2）设购买 A 种设备 m 台，则购买 B 种设备（20m ）台，根据总价单价 数量结合总费用不高于 15 万元，即可得出关于 m 的一元一次不等式，解之即可得出 m 的取值范围，取其内的最小正整数即可【解答】解：（1）设每台 A 种设备 x 万元
42、，则每台 B 种设备（x+0.7）万元，根据题意得： ，解得：x0.5经检验，x0.5 是原方程的解，x+0.71.2第 25 页（共 30 页）答：每台 A 种设备 0.5 万元，每台 B 种设备 1.2 万元（2）设购买 A 种设备 m 台，则购买 B 种设备（20m ）台，根据题意得：0.5m+1.2 （20m ）15，解得：m m 为整数，m13答：A 种设备至少要购买 13 台【点评】本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）根据数量总价单价结合花 3 万元购买 A 种设备和花 7.2 万元购买 B 种设备的数量相同，列出关于 x 的分式方程；（2）根据总
43、价单价数量结合总费用不高于 15万元，列出关于 m 的一元一次不等式七、(本题 12 分)25 （12 分）如图，已知正方形 ABCD 的边长为 4，点 P 是 AB 边上的一个动点，连接CP，过点 P 作 PC 的垂线交 AD 于点 E，以 PE 为边作正方形 PEFG，顶点 G 在线段 PC上对角线 EG、FP 相交于点 O（1）若 AP3，求 AE 的长；（2）连接 AC，判断点 O 是否在 AC 上，并说明理由；（3）在点 P 从点 A 到点 B 的运动过程中，正方形 PEFG 也随之运动，求 DE 的最小值【分析】 （1）只要证明APEBCP ，可得 由此即可解决问题；（2）点 O
44、在 AC 上过点 O 分别作 AD、AB 的垂线，垂足分别为 M、N，只要证明OMEONP，可得 OMON；（3）利用相似三角形的性质构建二次函数即可解决问题；【解答】解：（1）四边形 ABCD、四边形 PEFG 是正方形，第 26 页（共 30 页）AB EPG 90，PF EG ，ABBC 4， OEP45，AEP +APE90， BPC+APE90，AEP BPC，APE BCP， ，即 ，解得：AE ；（2）点 O 在 AC 上理由：过点 O 分别作 AD、AB 的垂线，垂足分别为 M、N，四边形 ABCD 是正方形，AOMAONA90，四边形 ANOM 是矩形，MON90，四边形 E
45、FGP 是正方形，OEOP ，MONEOP90，MOENOP，OMEONP，OMEONP，OM ON，点 O 在BAD 的平分线上，AC 是BAD 的平分线，点 O 在 AC 上第 27 页（共 30 页）（3）设 APx，则 BP4 x，APE BCP， ，即 ，解得：AEx x2 （ x2） 2+1，DE （x2） 2+3，所以 DE 的最小值为 3【点评】本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题，学会构建二次函数最值问题，属于中考压轴题八、 （本题 14 分）
46、26 （14 分）如图，顶点为 M 的抛物线 ya（x+1） 24 分别与 x 轴相交于点 A，B（点 A在点 B 的右侧） ，与 y 轴相交于点 C（0，3） （1）求抛物线的函数表达式；（2）判断BCM 是否为直角三角形，并说明理由（3）抛物线上是否存在点 N（点 N 与点 M 不重合） ，使得以点 A，B，C ，N 为顶点的四边形的面积与四边形 ABMC 的面积相等？若存在，求出点 N 的坐标；若不存在，请说明理由【分析】 （1）用待定系数法求出抛物线解析式即可；（2）由抛物线解析式确定出抛物线的顶点坐标和与 x 轴的交点坐标，用勾股定理的逆定理即可；（3）根据题意判断出点 N 只能在 x 轴上方的抛物线上，由已知四边形的面积相等转化出 SABN S BCM ，然后求出三角形 BCM 的面积，再建立关于点 N 的坐标的方程求解第 28 页（共 30 页）即可【解答】解：（1）抛物线 ya（x+1） 24 与 y 轴相交于点 C（0，3） 3a4，a1，抛物线解析式为 y（x +1） 24x 2+2x3，（2）BCM 是直角三角形理由：由（1）有，抛物线解析式为 y（x+1） 24，顶点为 M 的抛物线 ya（x+1） 24，M（1，4） ，由（1）抛物线解析式为 yx 2+2x3，令 y0，x 2+2x30 ，x 13，x 21，A（1，0） ，B（3，0）
