1、山东省济南市高新区 2017-2018 学年八年级（下）期末数学试卷一、选择题（本大题共 12 小题，每小题 4 分，共 48 分）1（4 分）下列方程中是一元二次方程的是（ ）A2x+10 By 2+x1 Cx 2+10 D x212（4 分）下列图形中，既是中心对称图形又是轴对称图形的是（ ）A BC D3（4 分）下列式子从左到右变形是因式分解的是（ ）Aa 2+4a21 a（a+4 ）21 Ba 2+4a21（a3）（a+7）C（a3）（a+7 ）a 2+4a21 Da 2+4a 21（a+2） 2254（4 分）要使分式 有意义，则 x
2、 的取值应满足（ ）Ax2 Bx1 Cx2 Dx 15（4 分）如图，在ABCD 中，AC、BD 相交于点 O，点 E 是 AB 的中点若 OE1cm，则 AD的长是（ ）cm A2 B3 C4 D56（4 分）如图，在 66 方格中有两个涂有阴影的图形 M、N，中的图形 M 平移后位置如所示，以下对图形 M 的平移方法叙述正确的是（ ）A向右平移 2 个单位，向下平移 3 个单位B向右平移 1 个单位，向下平移 3 个单位C向右平移 1 个单位，向下平移 4 个单位D向右平移 2 个单位，向下平移 4 个单位7（4 分）若方程 x24x +c
3、0 有两个不相等的实数根，则实数 c 的值可以是（ ）A6 B5 C4 D38（4 分）如图，在菱形 ABCD 中，M，N 分别在 AB，CD 上，且 AMCN，MN 与 AC 交于点O，连接 BO若DAC 28，则OBC 的度数为（ ）A28 B52 C62 D729（4 分）某工厂现在平均每天比原计划多生产 50 台机器，现在生产 600 台所需时间与原计划生产 450 台机器所需时间相同设原计划平均每天生产 x 台机器，根据题意，下面所列方程正确的是（ ）A B C D 10（4 分）下列多项式中，能用完全平方公式分解的是（
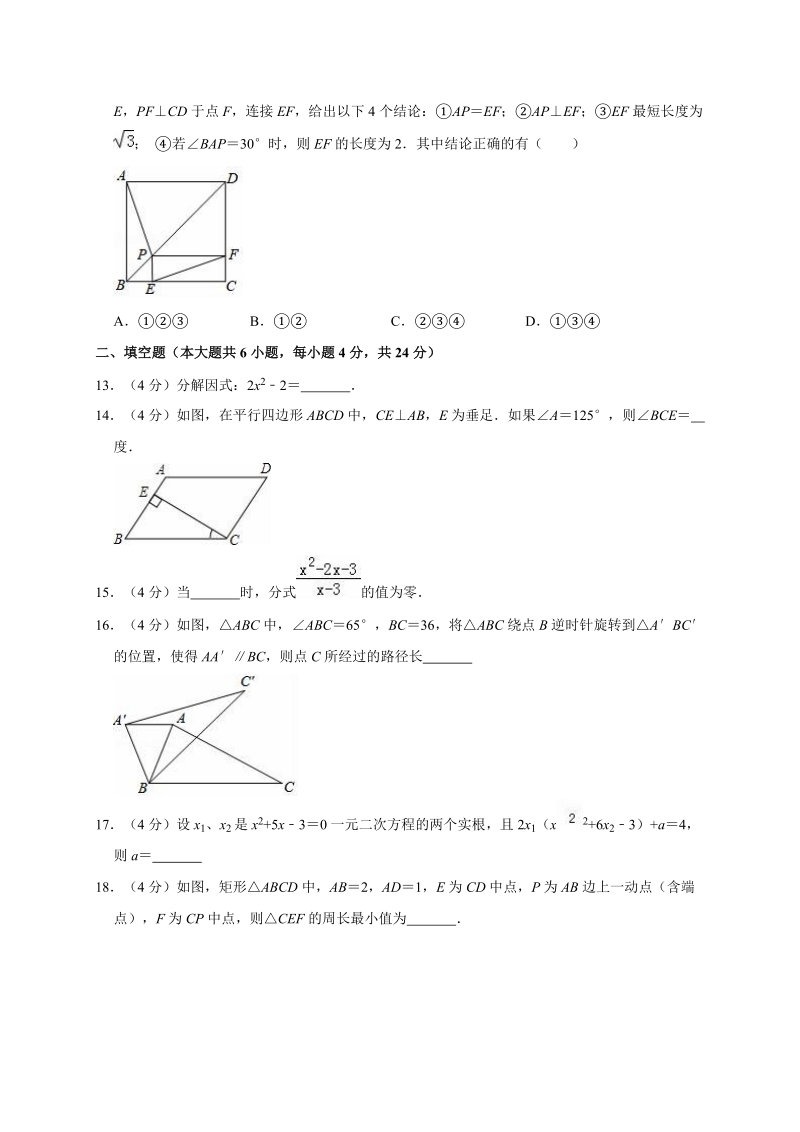
4、）Ax 2x+1 B12xy+x 2y2 C Da 2+b22ab11（4 分）如果把分式 中的 x 和 y 都扩大 3 倍，那么分式的值（ ）A扩大为原来的 3 倍 B缩小为原来的 倍C缩小为原来的 倍 D不变12（4 分）如图，P 为边长为 2 的正方形 ABCD 的对角线 BD 上任一点，过点 P 作 PEBC 于点E，PFCD 于点 F，连接 EF，给出以下 4 个结论：APEF；APEF；EF 最短长度为； 若BAP30时，则 EF 的长度为 2其中结论正确的有（ ）A B C D二、填空题（本大题共 6 小题，每小题 4 分，共 24 分）13（4 分）分
5、解因式：2x 22 14（4 分）如图，在平行四边形 ABCD 中，CEAB，E 为垂足如果A125，则BCE 度15（4 分）当 时，分式 的值为零16（4 分）如图，ABC 中，ABC 65，BC 36，将 ABC 绕点 B 逆时针旋转到ABC的位置，使得 AABC，则点 C 所经过的路径长 17（4 分）设 x1、x 2 是 x2+5x30 一元二次方程的两个实根，且 2x1（x 2+6x23）+a4，则 a 18（4 分）如图，矩形AB
6、CD 中，AB2，AD1，E 为 CD 中点，P 为 AB 边上一动点（含端点），F 为 CP 中点，则CEF 的周长最小值为 三、解答题（本大题共 9 小题，共 78 分）19（6 分）解方程： 1+20（6 分）如图所示，在四边形 ABCD 中，AEBD 于点 E，CFBD 于点F，AECF，BEDF求证：（1）ABE CDF；（2）四边形 ABCD 是平行四边形21（6 分）菱形 ABCD 在坐标系中的位置如图所示，点 A 的坐标为（1，0），点 B 的坐标为（1，0），点 D 在 y 轴上（1）求点 C、D 的坐标；（2）点 P 是对角线 AC 上一个动点，
7、当 OP+BP 最短时，求点 P 的坐标22（8 分）要建一个面积为 150m2 的长方形养鸡场，为了节约材料，鸡场的一边靠着原有的一条墙，墙长为 am，另三边用竹篱笆围成，已知篱笆总长为 35m（1）求鸡场的长、宽各是多少 m；（2）题中墙的长度 am 对解题有什么作用？23（8 分）已知ABC 在平面直角坐标系 xoy 中的位置如图所示（1）作ABC 关于点 O 成中心对称的A 1B1C1；（2）将A 1B1C1 向右平移 4 个单位，作出平移后的A 2B2C2；（3）在 x 轴上求作一点 P，使 PA1+PC2 的值最小，并求出这个最小值24（10 分）（1）已知：x1 是关于 x 的方
8、程 x22（ k2）x +k22k20 的一个根求 k 的值（2）先化简，再求值： ，其中 x2+ 25（10 分）如图，矩形 ABCD 中，AB6，BC8，再沿 EF 折叠，使得 D 点与 B 点重合，C 点的对应点为 G（1）求折痕 EF 的长；（2）将BEF 绕点 B 顺时针旋转，旋转角为 （0180），记旋转过程中的三角形为BEF，在旋转过程中设直线 EF与射线 EF、射线 ED 分别相交于点 M、N，当ENMN 时，求 FM 的长26（12 分）下面是某同学对多项式（x 24x3）（x 2 4x+1）+4 进行因式分解的过程解：设 x24xy原式（y3）（y +1）+4 （第一步）y
9、 22y+1 （第二步）（y1） 2 （第三步）（x 24x1） 2（第四步）回答下列问题：（1）该同学第二步到第三步运用了因式分解的 A提取公因式法 B平方差公式法 C完全平方公式法（2）请你模仿以上方法尝试对多项式（x 2+2x）（x 2+2x+2）+1 进行因式分解27（12 分）【观察发现】（1）如图 1，四边形 ABCD 和四边形 AEFG 都是正方形，且点 E 在边AB 上，连接 DE 和 BG，猜想线段 DE 与 BG 的数量关系和位置关系（只要求写出结论，不必说出理由）【
10、深入探究】（2）如图 2，将图 1 中正方形 AEFG 绕点 A 逆时针旋转一定的角度，其他条件与观察发现中的条件相同，观察发现中的结论是否还成立？请根据图 2 加以说明【拓展应用】（3）如图 3，直线 l 上有两个动点 A、B，直线 l 外有一点动点 Q，连接QA，QB，以线段 AB 为边在 l 的另一侧作正方形 ABCD，连接 QD随着动点 A、B 的移动，线段 QD 的长也会发生变化，若 QA，QB 长分别为 ，6 保持不变，在变化过程中，线段 QD的长是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由参考答案与试题解析一、选择题（本大题共 12 小题，每小题 4 分，共 48
11、 分）1【分析】一元二次方程有三个特点：（1）只含有一个未知数；（2）未知数的最高次数是2；（3）是整式方程要判断一个方程是否为一元二次方程，先看它是否为整式方程，若是，再对它进行整理如果能整理为 ax2+bx+c0（a0）的形式，则这个方程就为一元二次方程【解答】解：A、2x +10 未知数的最高次数是 1，故错误；B、y 2+x1 含有两个未知数，故错误；C、x 2+10 是一元二次方程，正确；D、是分式方程，故错误故选：C【点评】判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是 2这是一个需要识记的内容2【分析】根据中心对称图
12、形和轴对称图形对各选项分析判断即可得解【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、是中心对称图，不是轴对称图形，故本选项错误；C、既是中心对称图又是轴对称图形，故本选项正确；D、是轴对称图形，不是中心对称图形，故本选项错误故选：C【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部分重合3【分析】利用因式分解的定义，把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式，进而判断得出即可【解答】解；A、a 2+4a21a（a+4）21，不是
13、因式分解，故 A 选项错误；B、a 2+4a21（a3）（a+7），是因式分解，故 B 选项正确；C、（a3）（a+7 ）a 2+4a21，不是因式分解，故 C 选项错误；D、a 2+4a21 （a+2 ） 225，不是因式分解，故 D 选项错误；故选：B【点评】此题主要考查了因式分解的意义，正确把握因式分解的意义是解题关键4【分析】根据分式有意义的条件即可判断【解答】解：当 x+20 时，此时 x2故选：A【点评】本题考查分式有意义的条件，解题的关键是正确理解分式有意义的条件，本题属于基础题型5【分析】根据平行四边形的性质，可得出点 O 平分 BD，则 OE 是三角形 ABD 的中位线，则A
14、D2OE，继而求出答案【解答】解：四边形 ABCD 为平行四边形，BODO ，点 E 是 AB 的中点，OE 为ABD 的中位线，AD2OE ，OE1cm，AD2cm故选：A【点评】本题考查了平行四边形的性质和三角形的中位线定理，属于基础题，比较容易解答6【分析】根据平移前后图形 M 中某一个对应顶点的位置变化情况进行判断即可【解答】解：根据图形 M 平移前后对应点的位置变化可知，需要向右平移 1 个单位，向下平移3 个单位故选：B【点评】本题主要考查了图形的平移，平移由平移方向和平移距离决定，新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点7【分析】利用方程有两个不相等
15、的实数根时0，建立关于 c 的不等式，求出 c 的取值范围，再从选项中选答案【解答】解：由题意得b 24ac164c0，即 c 4，所以选项 D 符合故选：D【点评】总结：一元二次方程根的情况与判别式的关系：（1）0方程有两个不相等的实数根；（2）0方程有两个相等的实数根；（3）0方程没有实数根8【分析】根据菱形的性质以及 AMCN，利用 ASA 可得AMOCNO，可得 AOCO，然后可得 BOAC，继而可求得OBC 的度数【解答】解：四边形 ABCD 为菱形，ABCD，AB BC，MAONCO ，AMOCNO，在AMO 和CNO 中， ，AMOCNO （ASA ），AOCO，ABBC，BOA
16、C，BOC90，DAC28，BCADAC28，OBC902862故选：C【点评】本题考查了菱形的性质和全等三角形的判定和性质，注意掌握菱形对边平行以及对角线相互垂直的性质9【分析】设原计划平均每天生产 x 台机器，则实际平均每天生产（x+50）台机器，根据题意可得，现在生产 600 台所需时间与原计划生产 450 台机器所需时间相同，据此列方程即可【解答】解：设原计划平均每天生产 x 台机器，则实际平均每天生产（x+50）台机器，由题意得， 故选：B【点评】本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程10【分析】根据完全平方公式的结构特点
17、：必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的 2 倍，对各选项分析判断后利用排除法求解【解答】解：A、x 2x +1 不符合能用完全平方公式分解因式的式子的特点，故选项错误；B、12xy+x 2y2 符合能用完全平方公式分解因式的式子的特点，故选项正确；C、 不符合能用完全平方公式分解因式的式子的特点，故选项错误；D、a 2+b22 ab 不符合能用完全平方公式分解因式的式子的特点，故选项错误故选：B【点评】本题考查能用完全平方公式分解的式子的特点，熟记公式结构是解题的关键其中两项平方项的符号需相同；有一项是两底数积的 2 倍，是易错点11【分析
18、】根据分式的性质，可得答案【解答】解：把 x 和 y 都扩大 3 倍后，原式为 ，约分后仍为原式，分式值不变，故选：D【点评】本题考查了分式的基本性质，利用分式的基本性质是解题关键12【分析】连接 PC，可证得 ABPCBP，结合矩形的性质，可证得 PAEF，国判断 ；延长 AP 交 BC 于点 G，可证得 APEF ，可判断 ；求得 AP 的最小值即可求得 EF 的最短长度，可判断 ；当点 P 在点 B 或点 D 时，AP 有最大值 2，则可判断 ；可求得答案【解答】解：如图，连接 PC，四边形 ABCD 为正方形，ABBC， ABPCBP45，在ABP 和CBP 中，ABP CBP（SAS
19、），APPC，PEBC，PFCD，且FCE 90，四边形 PECF 为矩形，PCEF，APEF，故正确；延长 AP 交 BC 于点 G，由可得 PCE PFEBAP，PEAB，EPGBAP，EPGPFE，EPF 90，EPG+PEFPEG+PFE90，APEF，故正确；当 APBD 时，AP 有最小值 ，此时 P 为 BD 的中点，由可知 EFAP，EF 的最短长度为 ，故错误；当点 P 在点 B 或点 D 位置时，AP AB2，EFAP2，当BAP 30时，AP2，即 EF 的长度不可能为 2，故错误；综上可知正确的结论为故选：B【点评】本题主要考查正方形的性质及全等三角形的性质，构造三角形
20、全等证得 APEF 是解题的关键二、填空题（本大题共 6 小题，每小题 4 分，共 24 分）13【分析】先提取公因式 2，再根据平方差公式进行二次分解即可求得答案【解答】解：2x 222（x 21）2（x +1）（x1）故答案为：2（x+1）（x 1）【点评】本题考查了提公因式法，公式法分解因式，提取公因式后利用平方差公式进行二次分解，注意分解要彻底14【分析】根据平行四边形的性质和已知，可求出B，再进一步利用直角三角形的性质求解即可【解答】解：ADBC，A+B180，B18012555，CEAB，在 RtBCE 中，BCE 90B905535故答案为：35【点评】本题主要考查了平行四边形的
21、性质，运用平行四边形对边平行的性质，得到邻角互补的结论，这是运用定义求四边形内角度数的常用方法15【分析】分式 的值为零，即可得到一个关于 x 的分式方程，解这个方程即可【解答】解：根据题意得 0，解方程得 x11，x 23，当 x3 时，x 30，所以 x3 是增根，应舍去，即当 x1 时，分式 的值为零【点评】解分式方程首先在方程两边乘以最简公分母，化为整式方程再求解，注意一定要检验16【分析】首先根据旋转的性质可知 BAAB，即可得到BAABAA，由 AABC，得到AAB 68，再由三角形内角和定理得到ABA的度数，从而可得到CBC的度数，最后，依据扇形的弧长公式求解即可【解答】解：AB
22、C 绕点 A 逆时针旋转得到BAC，BAAB，BAA BAA，AABC，AAB ABC，ABC65，AAB65 ，ABA （180265）50，CBC ABA，CBC 50 点 C 所经过的路径长 10 故答案为：10【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角17【分析】利用根与系数的关系求出两根之和与两根之积，将已知的等式整理后，把求出的两根之和与两根之积代入列出关于 a 的方程，求出方程的解即可得到 a 的值【解答】解：x 1、x 2 是一元二次方程 x2+5x30 的两个实根，x 1+x25， x1x23，x 2
23、2+5x23，又2x 1（x 22+6x23）+a2x 1（x 22+5x2+x23）+a2x 1（3+x 23）+ a2x 1x2+a4，6+a4，解得：a10故答案为：10【点评】此题考查了一元二次方程根的判别式，以及根与系数的关系，一元二次方程ax2+bx+c0（ a0），当 b24ac 0 时，方程有两个不相等的实数根；当 b24ac0 时，方程有两个相等的实数根；当 b24ac0 时，方程没有实数根18【分析】根据三角形的中位线的性质得到 EF PD，得到 CCEFCE +CF+EFCE+ （CP +PD） （CD+PC +PD） CCDP ，当CDP 的周长最小时，CEF 的周长最
24、小；即 PC+PD 的值最小时，CEF 的周长最小；如图，作 D 关于 AB 的对称点D，连接 CD交 AB 于 P，于是得到结论【解答】解：E 为 CD 中点，F 为 CP 中点，EF PD，C CEF CE+CF+ EFCE + （CP+PD） （CD +PC+PD） CCDP ，当CDP 的周长最小时，CEF 的周长最小；即 PC+PD 的值最小时，CEF 的周长最小；如图，作 D 关于 AB 的对称点 D，连接 CD交 AB 于 P，ADAD BC，AD BC，四边形 ADBC 是平行四边形，APPB1，PDPC，CPPD ，C CEF CCDP +1，故答案为： +1【点
25、评】本题考查了轴对称最短距离问题，三角形的周长的计算，正确的作出图形是解题的关键三、解答题（本大题共 9 小题，共 78 分）19【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可得到分式方程的解【解答】解：两边都乘以 x3，得：3xx 31，解得：x2，检验：当 x2 时，x 32350，分式方程的解为 x2【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解解分式方程一定注意要验根20【分析】（1）由 AEBD，CFBD，根据垂直的定义得到AEBDFC，和已知AE CF，BFDE，推出ABECDF；（2）根据全等三角形
26、的性质得到 ABCD，ABECDF，进一步推出 ABCD，根据平行四边形的判定即可得到答案【解答】解：（1）AEBD，CFBD，AEB DFC90，在ABE 与CDF 中，ABE CDF（SAS）；（2）ABECDF，ABCD，ABECDF，ABCD，四边形 ABCD 是平行四边形【点评】本题主要考查了对平行四边形的性质和判定，垂线，平行线的判定，全等三角形的性质和判定等知识点的理解和掌握，能证出 ABCD 和 ABCD 是证此题的关键题型较好21【分析】（1）在 RtADO 中，利用勾股定理求得 OD 的长即可解决问题；（2）因为四边形 ABCD 是菱形，所以 B、D 关于直线 AC 对称，
27、设 OD 交 AC 于 P，此时OP+PB 的值最小，求出 OP 的长即可解决问题【解答】解：（1）点 A 的坐标为（1，0），点 B 坐标为（1，0），AB2，AO 1，四边形 ABCD 是菱形，ABAD CDBC2，CDAB，在 Rt ADO 中，OD ，D（0， ）， C（2， ）（2）四边形 ABCD 是菱形，B、D 关于直线 AC 对称，设 OD 交 AC 于 P，此时 OP+PB 的值最小，PO+ PBPD+POOD，即 PO+ PBPD+POOP +PB在 Rt AOP 中，PAO DAB30，OPOA tan30 ，P（0， ）【点评】本题考查轴对称最短问题、坐标与图形的性质、
28、菱形的性质等知识，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点22【分析】（1）本题可设鸡场的宽为 x，则长可用含 x 的代数式表示，从而这个鸡场的面积可用含 x 的代数式表示，列方程求解即可；（2）由于本题中的解有两个，因此 a 的取值范围可以确定哪个解才是符合题意的【解答】解：（1）设鸡场的宽为 xm，则长为（352x）m 依题意列方程为 x（352x ）150整理，得 2x235x +1500解方程，得 x110，x 27.5所以当 x10 时，352x 15；当 x7.5 时，352x 20故当鸡场的宽为 10m 时，长为 1
29、5m；当鸡场宽为 7.5m 时，长为 20m（2）当 a15 时，问题无解；当 15a20 时，问题有一解，即宽为 10m，长为 15m；当 a20 时，问题有两解，可建宽为 10m，长为 15m 或宽为 7.5m，长为 20m 的鸡场【点评】本题需要从实际出发，知道 a 对鸡场长度起到限制作用考查的知识点是一元二次方程的应用23【分析】（1）直接利用关于点对称点的性质得出对应点位置进而得出答案；（2）利用平移的性质进而得出对应点位置进而得出答案；（3）利用轴对称求最短路线的方法进而得出答案【解答】解：（1）如图所示：A 1B1C1，即为所求；（2）如图所示：A 2B2C2，即为所求；（3）如
30、图所示：点 P 即为所求，此时 PA1+PC2 的值最小为：AC 2 【点评】此题主要考查了旋转变换以及平移变换、利用轴对称求最短路线，正确得出对应点位置是解题关键24【分析】（1）将 x1 代入原方程，解之即可求出 k 值；（2）首先利用分式的混合运算法则化简原式，然后将 x2+ 代入，即可求得答案【解答】解：（1）x1 是关于 x 的方程 x22（k2）x +k22k20 的一个根，代入得：12（k2）+k 22k 20，k24k+30，解得：k1 或 3，当 k1 时，方程为 x2+2x3 0，此时方程有解；当 k3 时，方程为 x22x +10，此时方程有解，所以 k1 或 k3；（2
31、）原式 1+ ，当 x2+ 时，原式1+ 2 【点评】本题考查了分式的混合运算和求值，能正确根据分式的运算法则进行化简是解此题的关键25【分析】（1）设 AExFCFG，则 BEED 8x，由勾股定理得：AB 2+AE2BE 2，即62+x2（8x） 2，解得：x ，BE ，EF ；（2）由折叠性质得：BEFDEFBFE，得出DEFNMEF，证得四边形BEMF为平行四边形，由 BEBF，证得平行四边形 BEMF为菱形，得出 EMBE ，即可得出结果【解答】解：（1）如图所示：由折叠性质得：BEED ，DEFBEF，ADBC，DEFBFE，BEF BFE，BFBEED，ADBC，ADDE BC
32、BF ，即 AEFC ，设 AExFCFG，则 BEED 8x，在 Rt ABE 中，由勾股定理得：AB 2+AE2BE 2，即 62+x2（8x ） 2，解得：x ，BE8 ，EF ，（2）由折叠性质得：BEFDEFBFE，ENNM，DEFNMEF，EMBF，BEEF ，四边形 BEMF为平行四边形，由旋转性质得：BFBF 8x ，BEBF，平行四边形 BEMF为菱形，EMBE ，FMEFEM 【点评】本题考查了旋转的性质、勾股定理、矩形的性质、菱形的判定、平行四边形的判定等知识；本题综合性强，有一定难度，证出四边形 BEMF是菱形是解决问题的关键26【分析】利用换元法、完全平方公式进行因式
33、分解即可【解答】解：（1）该同学第二步到第三步运用了因式分解的完全平方公式法，故选：C（2）设 x2+2x y，原式y 2+2y+1，（y+1） 2，则（x 2+2x）（ x2+2x+2）+1 （x 2+2x+1） 2（x+1） 22（x+1） 4【点评】本题考查的是因式分解的应用，掌握换元思想、灵活运用完全平方公式是解题的关键27【分析】（1）根据正方形的性质，由 SAS 证明BAGDAE，得出DEBG，ABGADE，再由角的互余关系证出 DEBG 即可；（2）同（1）证明BAGDAE，从而证明结论；（3）以 OA 为边作正方形 QAGF，连接 QG、BG，则 QC OA4，当 G、Q 、B
34、 三点共线时，BG 最长，此时 BGQG+QB12，从而得出答案【解答】（1）解：DEBG，DEBG ；理由如下：延长 DE 交 BG 于 H，如图 1 所示：四边形 ABCD、四边形 AEFG 都是正方形，ABAD ，AGAE，EADBAG90，在BAG 与DAE 中， ，BAGDAE（SAS），DEBG ，ABG ADE，AGB+ABG 90，AGB+ADE 90，DHG90，DEBG ；（2）解：（1）中的结论成立，即 DEBG ，DEBG ；理由如下：如图 2 所示，四边形 ABCD、四边形 AEFG 都是正方形，BAAD ，AGAE，BADEAG90，BAG+BAEEAG+BAE，即BAGDAE，在BAG 与DAE 中， ，BAGDAE（SAS），DEBG ，ABG ADEAMD+ADE90，AMDBME，BME +ABG90，DNB90，DEBG ；（3）解：QD 存在最大值；理由如下：以 QA 为边作正方形 QAGF，连接 QG、BG，如图 3 所示：则 QG QA6，由（2）可得：QDBG，当 G、Q、B 三点共线时，BG 最长，此时 BGQG +QB6+612，即线段 QD 长的最大值为 12【点评】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、角的互余关系、对顶角相等、三点共线等知识；本题综合性强，证明三角形全等是解决问题的关键
