1、人教版九年级下学期28.1 锐角三角函数2019 年同步练习卷一选择题（共 10 小题）1已知 ， 是ABC 的两个角，且 sin，tan 是方程 2x23x+10 的两根，则ABC是（ ）A锐角三角形B直角三角形或钝角三角形C钝角三角形D等边三角形2已知：如图，O 1 与 O2 外切于 C 点，AB 一条外公切线， A、B 分别为切点，连接AC、BC设O 1 的半径为 R，O 2 的半径为 r，若 tanABC ，则 的值为（ ）A B C2 D33下列说法正确的个数有（ ）（1）对于任意锐角 ，都有 0sin 1 和 0cos1（2）对于任意锐角 1，
2、2，如果 1 2，那么 cos1cos 2（3）如果 sin1sin 2，那么锐角 1锐角 2（4）如果 cot1cot 2，那么锐角 1锐角 2A1 个 B2 个 C3 个 D4 个4已知 为锐角，下列结论：（1）sin +cos1；（2）若 45，则 sincos；（3）如果 cos ，则 60；（4） 1sin 其中正确结论的序号是（ ）第 2 页（共 16 页）A （1） （3） （4） B （2） （4） C （2） （3） （4） D （3） （4）5tan35cot1，则 等于（ ）A65 B35 C75 D556 为锐角，若 sin+cos ，则 si
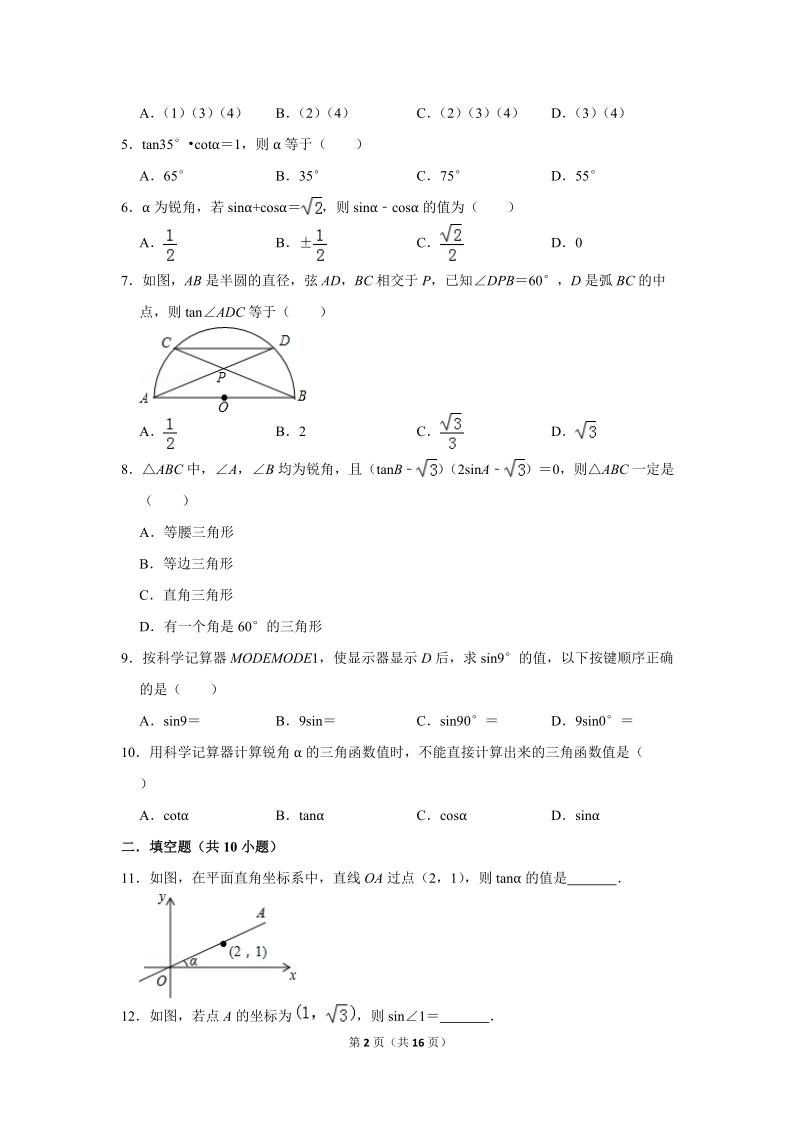
3、ncos 的值为（ ）A B C D07如图，AB 是半圆的直径，弦 AD，BC 相交于 P，已知DPB60，D 是弧 BC 的中点，则 tanADC 等于（ ）A B2 C D8ABC 中，A，B 均为锐角，且（tanB ） （2sinA ）0，则ABC 一定是（ ）A等腰三角形B等边三角形C直角三角形D有一个角是 60的三角形9按科学记算器 MODEMODE1，使显示器显示 D 后，求 sin9的值，以下按键顺序正确的是（ ）Asin9 B9sin Csin90 D9sin010用科学记算器计算锐角 的三角函数值时，不能直接计算出来的三角函
4、数值是（ ）Acot Btan Ccos Dsin二填空题（共 10 小题）11如图，在平面直角坐标系中，直线 OA 过点（2，1） ，则 tan 的值是 12如图，若点 A 的坐标为 ，则 sin1 第 3 页（共 16 页）13若 coscos ，且 、 都是锐角，则 （填“” 、 “”或“” ） 14比较大小：sin24 cos66，cos15 tan5515ABC 中，C90，tanA ，则 sinA+cosA
5、 16在 RtABC 中，C90，若 cosA ，则 tanA 17在ABC 中，C90，sinA ，则 tanB 18直角三角形中，若 sin35cos，则 19已知锐角 满足 cos ，则锐角 的度数是 度20比较三角函数值的大小：sin30 tan30 （填入“”或“” ） 三解答题（共 5 小题）21已知 ， 均为锐角，且 tan ，tan ，求 + 的度数22我们知道：sin30 ， tan30 ，sin4
6、5 ，tan45 1，sin60 ，tan60 ，由此我们可以看到 tan30sin30，tan45sin45，tan60sin60 ，那么对于任意锐角 ，是否可以得到 tansin 呢？请结合锐角三角函数的定义加以说明23如果 是锐角，且 cos ，求 sin，tan 的值24在ABC 中，C90，tanA ，求 cosB25计算：tan45cos 230+（32） 0第 4 页（共 16 页）人教版九年级下学期28.1 锐角三角函数2019 年同步练习卷参考答案与试题解析一选择题（共 10 小题）1已知 ， 是ABC 的两个角，且 sin，tan 是方程 2x23x+10 的两根，则ABC
7、是（ ）A锐角三角形B直角三角形或钝角三角形C钝角三角形D等边三角形【分析】先解出方程的两根，讨论 sin，tan 的值在三角形中，角的范围是（0，180） ，sin 必大于 0，此时只要考虑 tan 的值即可，若 tan0，则 为锐角；tan 小于 0，则 为钝角再把 x 的两个值分别代入 sin，tan 中，可求出 ， 的值，从而判断ABC 的形状【解答】解：由 2x23x +10 得：（2x 1） （x1）0，x 或 x1sin 0，tan0若 sin ，tan1，则 30，45，180 3045105，ABC 为钝角三角形若 sin 1，tan ，则 90，90，ABC 为
8、直角三角形故选：B【点评】本题易在 ， 上的取值出错，学生常常解出方程的两根后不知道如何判断，因此在解答时我们可对 x 的值分类讨论，从而判断出ABC 的形状2已知：如图，O 1 与 O2 外切于 C 点，AB 一条外公切线， A、B 分别为切点，连接AC、BC设O 1 的半径为 R，O 2 的半径为 r，若 tanABC ，则 的值为（ ）第 5 页（共 16 页）A B C2 D3【分析】根据切线长定理先证明ACB90，得直角三角形 ABC；再由 tanABC ，得两圆弦长的比；进一步求半径的比【解答】解：如图，连接 O2B，O 1A，过点 C 作两圆的公切线 CF，交于 AB
9、 于点 F，作O1EAC，O 2DBC，由垂径定理可证得点 E，点 D 分别是 AC，BC 的中点，由弦切角定理知，ABCFCB BO 2C，BACFCA AO 1C，AO 1O 2B，AO 1C+BO 2C180，FCB+ FCAACB 90，即ACB 是直角三角形，ABCBO 2DACO 1，设ABCBO 2DACO 1 ，则有 sin ，cos ，tan ，（tan ） 2 2故选：C【点评】本题综合性较强，综合了圆的有关知识，所以学生所学的知识要系统起来，不第 6 页（共 16 页）可单一3下列说法正确的个数有（ ）（1）对于任意锐角 ，都有 0sin 1 和 0cos1（
10、2）对于任意锐角 1， 2，如果 1 2，那么 cos1cos 2（3）如果 sin1sin 2，那么锐角 1锐角 2（4）如果 cot1cot 2，那么锐角 1锐角 2A1 个 B2 个 C3 个 D4 个【分析】理解锐角三角函数的定义：在直角三角形中，一个锐角的正弦值等于它的对边与斜边的比值；余弦值等于它的邻边与斜边的比值；正切值等于它的对边与邻边的比值了解锐角三角函数的变化规律：正弦值和正切值随着角的增大而增大；余弦值随着角的增大而减小【解答】解：（1）根据锐角三角函数的概念，三边都是正数，且斜边最大，故正确；（2）余弦值是随着角的增大而减小，故错误；（3）正弦值是随着角的增大而增大，故
11、正确；（4）余切值是随着角的增大而减小，故正确所以正确的有（1） ， （3） ， （4） 故选：C【点评】理解锐角三角函数的概念，掌握锐角三角函数值的变化规律4已知 为锐角，下列结论：（1）sin +cos1；（2）若 45，则 sincos；（3）如果 cos ，则 60；（4） 1sin 其中正确结论的序号是（ ）A （1） （3） （4） B （2） （4） C （2） （3） （4） D （3） （4）【分析】根据锐角三角函数的定义、互余角的三角函数的关系、锐角三角函数的增减性、特殊角的三角函数值及绝对值的定义求解【解答】解：（1）如果 30，那么第 7 页（共 16 页）
12、sin ，cos ，sin+cos 1，错误；（2）9045，0 90 45，sinsin （90） ，sin cos，正确；（3）cos60 ，余弦函数随角增大而减小， 如果 cos ，则 60，正确；（4）sin 1，sin 10， |sin1|1sin ，正确故正确结论的序号是（2） （3） （4） 故选：C【点评】本题综合性较强，涉及知识点较多，须认真仔细5tan35cot1，则 等于（ ）A65 B35 C75 D55【分析】根据同角三角函数的关系 tancot1 解答即可【解答】解：由 tan35cot1，得 35故选：B【点评】本题考查了同角的三角函数的关系中的同角
13、的正切和余切的关系6 为锐角，若 sin+cos ，则 sincos 的值为（ ）A B C D0【分析】将两式分别两边平方，利用 sin2+cos21，求出 sincos 的值，解答即可【解答】解：sin+cos ，（sin +cos） 22，即 sin2+cos2+2sincos2又sin 2+cos21，2sincos1（sin cos） 2sin 2+cos22sin cos12sin cos110sin cos0故选：D【点评】本题利用了同角的三角函数的关系 sin2+cos21 来进行化简求值的7如图，AB 是半圆的直径，弦 AD，BC 相交于 P，已知DPB60，D
14、 是弧 BC 的中第 8 页（共 16 页）点，则 tanADC 等于（ ）A B2 C D【分析】连接 AC，则ACB90，CAP30BAD ，求出ABC 的度数，根据圆周角定理求出 tanADC 的值【解答】解：连接 ACAB 为直径，ACB 90DPBAPC60，CAP30D 是弧 BC 的中点，CAPBAD，CAB 60ABC30ADC则 tanADC 故选：C【点评】本题较难，考查了圆周角定理和特殊角的三角函数值8ABC 中，A，B 均为锐角，且（tanB ） （2sinA ）0，则ABC 一定是（ ）A等腰三角形B等边三角形C直角三角形D有一个角是 60的三
15、角形【分析】根据题意，tanB 0 或 2sinA 0根据特殊角的三角函数值求解即可【解答】解：ABC 中，A，B 均为锐角，且（tanB ） （2sinA ）0，tanB 0 或 2sinA 0，第 9 页（共 16 页）即 tanB 或 sinA B60或A60ABC 有一个角是 60故选：D【点评】本题重点考查特殊角的三角函数值、三角形形状的判断，注意分类讨论9按科学记算器 MODEMODE1，使显示器显示 D 后，求 sin9的值，以下按键顺序正确的是（ ）Asin9 B9sin Csin90 D9sin0【分析】本题要求熟练应用计算器【解答】解：按科学记算器 MODE M
16、ODE 1，使显示器显示 D 后，即进入角度制单位，只需键入 sin 9即可故选：C【点评】本题要求同学们能熟练应用计算器，熟悉计算器的各个按键的功能10用科学记算器计算锐角 的三角函数值时，不能直接计算出来的三角函数值是（ ）Acot Btan Ccos Dsin【分析】本题要求熟练应用计算器进行计算【解答】解：用科学记算器计算锐角 的三角函数值时，只能计算正弦、余弦、正切的值，要计算余切的值，需先计算正切值，在借助倒数进行计算得出答案，故答案为 A【点评】本题考查计算器的基本功能二填空题（共 10 小题）11如图，在平面直角坐标系中，直线 OA 过点（2，1） ，则 tan 的
17、值是 【分析】根据正切函数是对边比邻边，可得答案第 10 页（共 16 页）【解答】解：如图 ，tan 故答案为： 【点评】本题考查了锐角三角函数，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边12如图，若点 A 的坐标为 ，则 sin1 【分析】根据勾股定理，可得 OA 的长，根据正弦是对边比斜边，可得答案【解答】解：如图， ，由勾股定理，得OA 2sin1 ，故答案为： 【点评】本题考查了锐角三角函数，利用勾股定理得出 OA 的长是解题关键13若 coscos ，且 、 都是锐角，则 （填“” 、 “”或“”
18、） 【分析】根据锐角余弦函数随角的增大而减小，可得答案【解答】解：由 coscos ，且 、 都是锐角，则 故答案为：第 11 页（共 16 页）【点评】本题考查了锐角三角函数的增减性，利用锐角余弦函数随角的增大而减小是解题关键14比较大小：sin24 cos66，cos15 tan55 【分析】根据一个角的余弦等于它余角的正弦，可得答案；根据锐角的余弦随随角的增大而减小，可得 ocs15与 cos0的大小关系，根据锐角的正切函数随角的增大而增大，可得 tan45与 tan55d 的大小关系【解答】解：cos66sin（9066）sin24，cos15c
19、os01，1tan45tan55 ，cos151tan55，故答案为：，【点评】本题考查了锐角三角函数的增减性，利用了锐角的余弦随角的增大而减小，锐角的正切函数随角的增大而增大15ABC 中，C90，tanA ，则 sinA+cosA 【分析】根据 tanA 和三角函数的定义画出图形，进而求出 sinA 和 cosA 的值，再求出 sinA+cosA 的值【解答】解：如图 ，tanA ，设 AB5x，则 BC4x，AC3x，则有：sinA+cosA + + ，故答案为： 【点评】此题考查了锐角三角函数的定义，只要画出图形，即可将正弦、余弦、正切函数联系起来，进而得出结
20、论16在 RtABC 中，C90，若 cosA ，则 tanA 【分析】根据 cosA ，设出关于两边的代数表达式，再根据勾股定理求出第三边长的第 12 页（共 16 页）表达式即可推出 tanA 的值【解答】解：cosA 知，设 bx，则 c4x，根据 a2+b2c 2 得 a xtanA 故答案为： 【点评】本题考查了锐角三角函数定义的应用，利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值17在ABC 中，C90，sinA ，则 tanB 【分析】根据同角三角函数关系，可得 cot
21、A，根据一个角的正切等于它余角的余切，可得答案【解答】解：cosA ，cotA ，ABC 中，C90，sinA ，tanBcotA ，故答案为： 【点评】本题考查了互余两角三角函数关系，同角三角函数关系，可得 cotA，根据一个角的正切等于它余角的余切18直角三角形中，若 sin35cos，则 55 【分析】根据在直角三角形中，A+B90时，正余弦之间的关系为：一个角的正弦值等于这个角的余角的余弦值，即 sinAcos（90A） ，求解即可【解答】解：根据直角三角形中正余弦之间的关系，可得：sin35cos（9035）cos55，55故答案为：55【点评】本题考查了互余两角三角函数的关系，解答
22、本题的关键在于熟练掌握互余两角三角函数的关系：一个角的正弦值等于这个角的余角的余弦值，即 sinAcos（90A） 19已知锐角 满足 cos ，则锐角 的度数是 60 度第 13 页（共 16 页）【分析】根据特殊角三角函数值，可得答案【解答】解：由锐角 满足 cos ，则锐角 的度数是 60 度，故答案为：60【点评】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键20比较三角函数值的大小：sin30 tan30 （填入“”或“” ） 【分析】根据特殊角三角函数值，可得答案【解答】解：sin30 ，tan30 ， ，即 sin30tan30 ，故答案为：【点评】本题考
23、查了特殊角三角函数值，熟记特殊角三角函数值是解题关键三解答题（共 5 小题）21已知 ， 均为锐角，且 tan ，tan ，求 + 的度数【分析】如图，在ABC 中，AD BC 于 D，设DAB，DAC，作 CHAB于 H由 tan ，可以假设 BD3a，AD 6a，由 tan ，可得CD2a，求出 CH，AH，证明ACH 是等腰直角三角形即可解决问题【解答】解：如图，在ABC 中，AD BC 于 D，设DAB，DAC，作CHAB 于 Htan ，可以假设 BD3a，AD6a，tan ，CD2a，在 Rt ADB 中，AB 3 a，第 14 页（共 16 页） BCAD ABCH，CH 2 a
24、，在 Rt CBH 中， BH a，AH2 a，AHCH，CHA90+CAH45【点评】考查锐角三角函数的知识，解题的关键是学会构造直角三角形解决问题，学会利用数形结合的思想思考问题22我们知道：sin30 ， tan30 ，sin45 ，tan45 1，sin60 ，tan60 ，由此我们可以看到 tan30sin30，tan45sin45，tan60sin60 ，那么对于任意锐角 ，是否可以得到 tansin 呢？请结合锐角三角函数的定义加以说明【分析】由直角三角形中斜边最长及锐角三角函数的定义可以证明：对于任意锐角 ，都有 tansin【解答】解：对于任意锐角 ，都有 tansin ，理
25、由如下：如图，ABC 中，C90，A、B、C 的对边分别是 a、b、c，设A则 tan ，sin ，bc， ，tan sin【点评】本题考查了锐角三角函数的定义，在 RtABC 中，C90（1）正弦：我们把锐角 A 的对边 a 与斜边 c 的比叫做A 的正弦，记作 sinA即 sinAA 的对边：斜边a：c第 15 页（共 16 页）（2）余弦：锐角 A 的邻边 b 与斜边 c 的比叫做A 的余弦，记作 cosA即 cosAA 的邻边：斜边b：c（3）正切：锐角 A 的对边 a 与邻边 b 的比叫做A 的正切，记作 tanA即 tanAA 的对边：A 的邻边a：b（4）三角函数：锐角 A 的正
26、弦、余弦、正切都叫做A 的锐角三角函数23如果 是锐角，且 cos ，求 sin，tan 的值【分析】根据同角的三角函数关系式：sin 2+cos21，tan ，进行计算【解答】解：cos ，sin ，tan 2 【点评】熟练运用同角的同角三角函数关系式进行求解24在ABC 中，C90，tanA ，求 cosB【分析】先根据正切值求出A 的度数，根据直角三角形的性质得到B 的度数，再根据余弦的定义即可求解【解答】解：tanA ，A60 &nb
27、sp; A+B90，B906030 cosB 【点评】此题考查的知识点是特殊角的三角函数值，关键明确求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值25计算：tan45cos 230+（32） 0【分析】根据特殊角三角函数值，零次幂，可得答案【解答】解：原式1（ ） 2+12 【点评】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键
