1、第 1 页（共 28 页）2019 年黑龙江省哈尔滨市松北区中考数学一模试卷一、选择题（每题 3 分，共计 30 分）1 （3 分） 的相反数是（ ）A3 B3 C D2 （3 分）下列图形中，是中心对称图形的是（ ）A BC D3 （3 分）下列计算正确的是（ ）A3a+4b7ab B （ab 3） 3ab 6C （a+2） 2a 2+4 Dx 12x6x 64 （3 分）下列四个几何体中，左视图为圆的几何体是（ ）A BC D5 （3 分）抛物线 y3（x 4） 2+5 的顶点坐标为（ ）A （4，5） B （4，5） C （4，5） D （4，5）6 （3 分）在 RtABC 中，C90
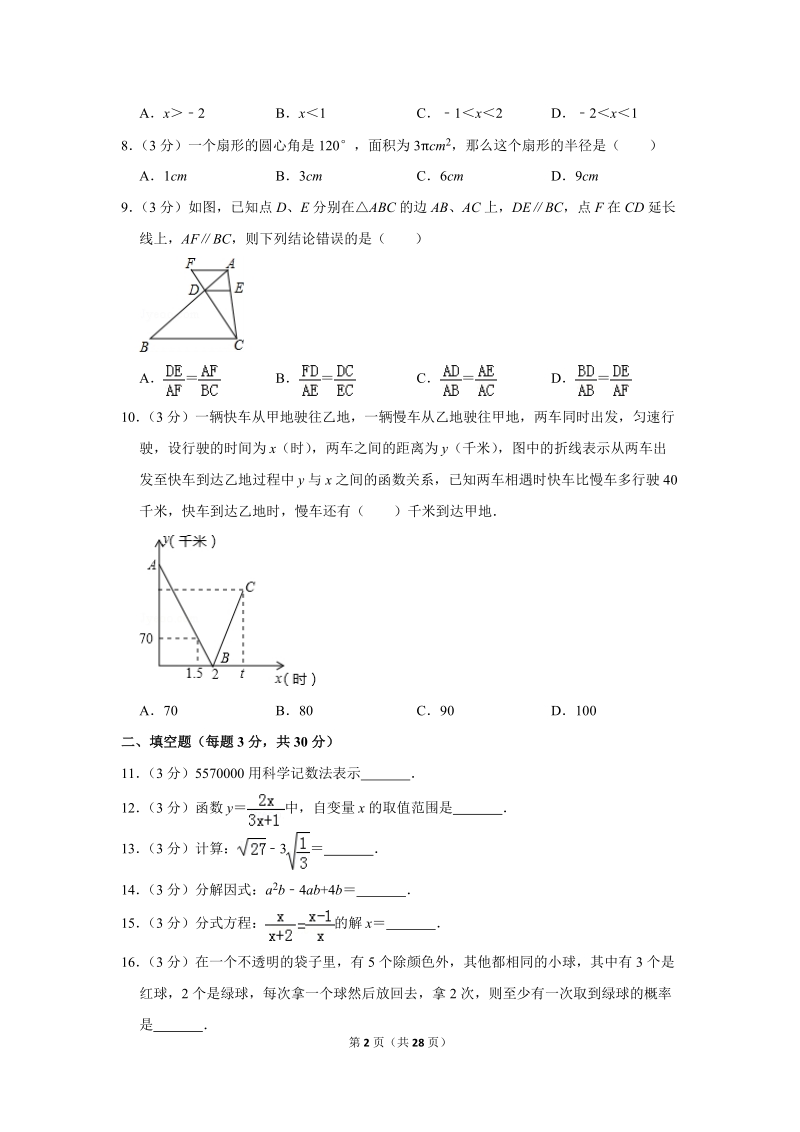
2、，BC3，AB5，则 cosB 的值等于（ ）A B C D7 （3 分）不等式组 的解集是（ ）第 2 页（共 28 页）Ax2 Bx1 C1x2 D2x 18 （3 分）一个扇形的圆心角是 120，面积为 3cm2，那么这个扇形的半径是（ ）A1cm B3cm C6cm D9cm9 （3 分）如图，已知点 D、 E 分别在ABC 的边 AB、AC 上，DEBC，点 F 在 CD 延长线上，AF BC ，则下列结论错误的是（ ）A B C D 10 （3 分）一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶，设行驶的时间为 x（时） ，两车之间的距离为 y（千米） ，图
3、中的折线表示从两车出发至快车到达乙地过程中 y 与 x 之间的函数关系，已知两车相遇时快车比慢车多行驶 40千米，快车到达乙地时，慢车还有（ ）千米到达甲地A70 B80 C90 D100二、填空题（每题 3 分，共 30 分）11 （3 分）5570000 用科学记数法表示 12 （3 分）函数 y 中，自变量 x 的取值范围是 13 （3 分）计算： 3 14 （3 分）分解因式：a 2b4ab+4b 15 （3 分）分式方程： 的解 x 16 （3 分）在一个不透明的袋子里，有 5 个除颜色外，其他都相同的小球，其中有 3 个是红球，2 个是绿球，每次拿一个球然后放回去，拿 2 次，则至
4、少有一次取到绿球的概率是 第 3 页（共 28 页）17 （3 分）帐篷厂原计划生产 7200 顶帐篷，后来为了支援灾区，要求工厂生产的帐篷比原计划多 20%，并需要提前 4 天完场任务已知实际生产时每天比原计划多生产 720 顶帐篷，设实际每天生产 x 顶帐篷，根据题意可列方程为 18 （3 分）如图，函数 y 和 y 的图象分别是 l1 和 l2设点 P 在 l1 上，PC x 轴，垂足为 C，交 l2 于点 A，PD y 轴，垂足为 D，交 l2 于点 B，则PAB 的面积为 19 （3 分）如图，将边长为 12 的正方形 ABCD 沿其对角线 AC 剪开，再把ABC 沿着 AD方向向右
5、平移，得到ABC ，当两个三角形重叠部分的面积为 32 时，它移动的距离 AA等于 20 （3 分）如图，AD 和 BE 分别为三角形 ABC 的中线和角平分线，ADBE ，若ADBE4，则 AC 的长 三、解答题（共 60 分，其中 21、22 题各 7 分，23、24 题各 8 分，25、26、27 题各 10 分）21 （7 分）先化简，再求代数式 （x2y ）的值，其中 xtan60，y2sin30 第 4 页（共 28 页）22 （7 分）如图，在每个小正方形的边长均为 1 的方格纸中，线段 AB 的端点 A、B 均在小正方形的顶点上（1）在方格纸中画出以 AB 为一条直角边的等腰直
6、角ABC，顶点 C 在小正方形的顶点上；（2）在方格纸中画出ABC 的中线 BD，将线段 DC 绕点 C 顺时针旋转 90得到线段CD，画出旋转后的线段 CD，连接 BD，直接写出四边形 BDCD的面积23 （8 分）某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取了本校部分学生进行问卷调查（必选且只选一类节目） ，将调查结果进行整理后，绘制了如下不完整的条形统计图和扇形统计图，其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的 3 倍还多 1 人请根据所给信息解答下列问题：（1）求本次抽取的学生人数（2）补全条形图，在扇形统计图中的横线上填上正确的数值，并直接
7、写出“体育”对应的扇形圆心角的度数（3）该校有 3000 名学生，求该校喜爱娱乐节目的学生大约有多少人？24 （8 分）如图，在 RtABC 中，BAC90，D 是 BC 的中点，连接 AD，E 为 AD 的中点，过 A 作 AFBC 交 BE 延长线于 F，连接 CF（1）求证：四边形 ADCF 是菱形；（2）在不添加任何辅助线的情况下，请直接写出与ACD 面积相等的三角形（不包含ACD） 第 5 页（共 28 页）25 （10 分）我市城市绿化工程招标，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要 60 天，若由甲队先做 20 天，再由甲、乙合作 12 天，共完成总工作量的三分
8、之二（1）乙队单独完成这项工程需要多少天？（2）甲队施工 1 天需付工程款 4.5 万元，乙队施工一天需付工程款 2 万元，该工程由甲乙两队合作若干天后，再由乙队完成剩余工作，若要求完成此项工程的工程款不超过186 万元，求甲、乙两队最多合作多少天？26 （10 分）如图 1，ABC 为O 的内接三角形，AD 为O 的直径，AD 与 BC 相交于点F，DE 为 O 的切线，交 AC 的延长线于 E（1）求证：EB；（2）如图 2，若CFD3DAE，求证：ACBC ；（3）如图 3，在（2）的条件下，过点 A 作 AGBC 于点 G，AG 的延长线交 BD 于点H，点 H 为 BD 的中点若 C
9、E1，求 FG 的长27 （10 分）在平面直角坐标系中，O 为坐标原点，抛物线 yax 2+c 交 x 轴于点 A、B（A左 B 右） ，交 y 轴于点 C，OBOC，且 SABC 4（1）如图 1，求 a、c 的值；（2）如图 2，点 P 在第三象限的抛物线上，BP 交 y 轴于点 D，设点 P 的横坐标为 t，线段 CD 的长为 d，求 d 与 t 之间的函数关系式，并直接写出自变量 t 的取值范围；（3）如图 3，在（2）的条件下，点 Q 在线段 PD 上，若PC CQ，2PCDPCQ 45，求点 P 的坐标第 6 页（共 28 页）第 7 页（共 28 页）2019 年黑龙江省哈尔滨
10、市松北区中考数学一模试卷参考答案与试题解析一、选择题（每题 3 分，共计 30 分）1 （3 分） 的相反数是（ ）A3 B3 C D【分析】求一个数的相反数，即在这个数的前面加负号【解答】解：根据相反数的定义，得 的相反数是 故选：D【点评】本题考查的是相反数的求法2 （3 分）下列图形中，是中心对称图形的是（ ）A BC D【分析】根据中心对称图形的概念和各图的特点解答即可求解【解答】解：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误；故选：B【点评】此题主要考查了中心对称图形，注意把握：中心对称
11、图形是要寻找对称中心，旋转 180 度后与原图重合3 （3 分）下列计算正确的是（ ）A3a+4b7ab B （ab 3） 3ab 6第 8 页（共 28 页）C （a+2） 2a 2+4 Dx 12x6x 6【分析】直接利用同底数幂的乘除运算法则以及积的乘方运算法则、合并同类项法则分别计算得出答案【解答】解：A、3a+4b，无法计算，故此选项错误；B、 （ab 3） 3a 3b9，故此选项错误；C、 （a+2） 2a 2+4a+4，故此选项错误；D、x 12x6x 6，故此选项正确故选：D【点评】此题主要考查了同底数幂的乘除运算以及积的乘方运算、合并同类项等知识，正确掌握运算法则是解题关键4
12、 （3 分）下列四个几何体中，左视图为圆的几何体是（ ）A BC D【分析】根据左视图是从左边看所得到的图形逐一判断可得【解答】解：A、球的左视图是圆，故选项正确；B、正方体的左视图是正方形，故选项错误；C、圆锥的左视图是等腰三角形，故选项错误；D、圆柱的左视图是长方形，故选项错误；故选：A【点评】此题主要考查了左视图，关键是掌握左视图所看的位置5 （3 分）抛物线 y3（x 4） 2+5 的顶点坐标为（ ）A （4，5） B （4，5） C （4，5） D （4，5）【分析】直接根据二次函数的顶点坐标式进行解答即可【解答】解：二次函数的解析式为 y3（x4） 2+5，其顶点坐标为：（4，5）
13、 第 9 页（共 28 页）故选：D【点评】本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键6 （3 分）在 RtABC 中，C90，BC3，AB5，则 cosB 的值等于（ ）A B C D【分析】根据余弦函数的定义，角的邻边比斜边，可得答案【解答】解：在 RtABC 中，C90，BC3，AB5，得 cosB ，故选：D【点评】本题考查了锐角三角函数的定义，锐角的余弦等于角的邻边比斜边7 （3 分）不等式组 的解集是（ ）Ax2 Bx1 C1x2 D2x 1【分析】首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集【解答】解： ，解得 x2，解得 x1，则不等式组
14、的解集是：2x1故选：D【点评】本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到8 （3 分）一个扇形的圆心角是 120，面积为 3cm2，那么这个扇形的半径是（ ）A1cm B3cm C6cm D9cm【分析】根据扇形的面积公式：S 代入计算即可解决问题【解答】解：设扇形的半径为 R，由题意：3 ，解得 R3，R0，R3cm，第 10 页（共 28 页）这个扇形的半径为 3cm故选：B【点评】本题考查扇形的面积公式，关键是记住扇形的面积公式：S LR（L 是弧长，R
15、是半径） ，属于中考常考题型9 （3 分）如图，已知点 D、 E 分别在ABC 的边 AB、AC 上，DEBC，点 F 在 CD 延长线上，AF BC ，则下列结论错误的是（ ）A B C D 【分析】由 AFBC，DE BC，得到 AFDE，根据平行线分线段成比例定理即可得到结论【解答】解：AFBC，DEBC，AFDE ， ， ， ，故 A 错误，AFDE ， ，故 B 正确，DEBC， ，故 C 正确，AFDE ， ，AFBC， ， ，故 D 正确，故选：A第 11 页（共 28 页）【点评】本题考查了平行线分线段成比例定理，熟练掌握平行线分线段成比例定理是解题的关键10 （3 分）一辆快
16、车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶，设行驶的时间为 x（时） ，两车之间的距离为 y（千米） ，图中的折线表示从两车出发至快车到达乙地过程中 y 与 x 之间的函数关系，已知两车相遇时快车比慢车多行驶 40千米，快车到达乙地时，慢车还有（ ）千米到达甲地A70 B80 C90 D100【分析】求出相遇前 y 与 x 的关系式，确定出甲乙两地的距离，进而求出两车的速度，即可确定出所求【解答】解：设第一段折线解析式为 ykx+b，把（1.5，70）与（2，0）代入得： ，解得： ，即 y140x+280，令 x0，得到 y280，即甲乙两对相距 280 千米，设两车相
17、遇时，乙行驶了 x 千米，则甲行驶了（x+40）千米，根据题意得：x+x +40280，解得：x120，即两车相遇时，乙行驶了 120 千米，则甲行驶了 160 千米，甲车的速度为 80 千米/时，乙车速度为 60 千米/ 时，根据题意得：（280160）801.5（小时） ，1.56090（千米） ，2801209070（千米） ，则快车到达乙地时，慢车还有 70 千米到达甲地，第 12 页（共 28 页）故选：A【点评】此题考查了一次函数的应用，弄清题意是解本题的关键二、填空题（每题 3 分，共 30 分）11 （3 分）5570000 用科学记数法表示 5.5710 6 【分析】科学记数
18、法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：5570000 用科学记数法表示 5.57106故答案为：5.5710 6【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n 的形式，其中 1|a| 10 ，n 为整数，表示时关键要正确确定 a 的值以及 n 的值12 （3 分）函数 y 中，自变量 x 的取值范围是 x 【分析】根据分母不等于 0 列式计算即可得解【解答】解：由题意得，3x+
19、10，解得，x 故答案为：x 【点评】本题考查了函数自变量的范围，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为 0；（3）当函数表达式是二次根式时，被开方数非负13 （3 分）计算： 3 2 【分析】直接化简二次根式，进而合并求出答案【解答】解：原式3 3 2 故答案为：2 【点评】此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键14 （3 分）分解因式：a 2b4ab+4b b（a2） 2 【分析】考查了对一个多项式因式分解的能力本题属于基础题，当一个多项式有公因式，将其分解因式时应先提取公因式，再对余下的多
20、项式继续分解此题应先提公因式，第 13 页（共 28 页）再用完全平方公式【解答】解：a 2b4ab+4bb（a 24a+4）b（a2） 2【点评】本题考查因式分解的概念，注意必须将式子分解到不能分解为止完全平方公式：a 22ab+b2（ab） 215 （3 分）分式方程： 的解 x 2 【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可得到分式方程的解【解答】解：去分母得：x 2x 2+x2，解得：x2，经检验 x2 是分式方程的解故答案为：2【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想” ，把分式方程转化为整式方程求解解分式方程一定注意要验根
21、16 （3 分）在一个不透明的袋子里，有 5 个除颜色外，其他都相同的小球，其中有 3 个是红球，2 个是绿球，每次拿一个球然后放回去，拿 2 次，则至少有一次取到绿球的概率是 【分析】列举出所有情况，数出至少有一次取到绿球的情况占总情况数的多少即可【解答】解：列表如下：红 1 红 2 红 3 绿 1 绿 2红 1 （红 1，红1）（红 1，红2）（红 1，红3）（红 1，绿 1 ）（红 1，绿2）红 2 （红 2，红1）（红 1，红2）（红 2，红3）（红 2，绿1）（红 2，绿2）红 3 （红 3，红1）（红 3，红2）（红 3，红3）（红 3，绿1）（红 3，绿2）绿 1 （绿 1，红1
22、）（绿 1，红2）（绿 1，红3）（绿 1，绿1）（绿 1，绿2）绿 2 （绿 2，红 （绿 2，红 （绿 2，红 （绿 2，绿 （绿 2，绿第 14 页（共 28 页）1） 2） 3） 1） 2）由列表可知共 25 种等可能的结果，其中至少有一次取到绿球的结果有 16 种，所以拿 2 次，则至少有一次取到绿球的概率 ，故答案为： 【点评】此题考查的是用列表法或树状图法求概率列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验用到的知识点为：概率所求情况数与总情况数之比17 （3 分）帐篷厂原计划生产
23、7200 顶帐篷，后来为了支援灾区，要求工厂生产的帐篷比原计划多 20%，并需要提前 4 天完场任务已知实际生产时每天比原计划多生产 720 顶帐篷，设实际每天生产 x 顶帐篷，根据题意可列方程为 【分析】关键描述语为：“实际每天比原计划每天多生产 720 顶” ；等量关系为：计划完成帐篷的天数实际完成帐篷的天数4，若设实际每天生产 x 顶帐篷，则有：【解答】解：设实际每天生产 x 顶帐篷根据题意得： 故答案是： 【点评】本题考查由实际问题抽象出分式方程，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键18 （3 分）如图，函数 y 和 y 的图象分别是 l1 和 l2设点 P 在
24、 l1 上，PC x 轴，垂足为 C，交 l2 于点 A，PD y 轴，垂足为 D，交 l2 于点 B，则PAB 的面积为 8 第 15 页（共 28 页）【分析】设 P 的坐标是（a， ） ，推出 A 的坐标和 B 的坐标，求出APB90，求出PA、PB 的值，根据三角形的面积公式求出即可【解答】解：方法一：点 P 在 y 上，|x p|yp|k|1，设 P 的坐标是（a， ） （a 为正数） ，PAx 轴，A 的横坐标是 a，A 在 y 上，A 的坐标是（a， ） ，PBy 轴，B 的纵坐标是 ，B 在 y 上，代入得： ，解得：x3a，B 的坐标是（3a， ） ，PA| （ ）| ，PB
25、| a（3a）|4a，PAx 轴，PBy 轴，x 轴y 轴，PAPB，PAB 的面积是： PAPB 4a8故答案为：8方法二：函数 y 和 y 的图象分别是 l1 和 l2点 P 在 l1 上，PC x 轴，垂足为 C，交 l2 于点 A，PDy 轴，垂足为 D，交 l2 于点 B， ， ，第 16 页（共 28 页）由矩形 DOPC矩形 BEAP，故 S 矩形 BEAP16S 矩形 DOPC，16116，则 SAPC 8【点评】本题考查了反比例函数和三角形面积公式的应用，关键是能根据 P 点的坐标得出 A、B 的坐标，本题具有一定的代表性，是一道比较好的题目19 （3 分）如图，将边长为 1
26、2 的正方形 ABCD 沿其对角线 AC 剪开，再把ABC 沿着 AD方向向右平移，得到ABC ，当两个三角形重叠部分的面积为 32 时，它移动的距离 AA等于 4 或 8 【分析】根据平移的性质，结合阴影部分是平行四边形，AAH 与HCB都是等腰直角三角形，则若设 AAx，则阴影部分的底长为 x，高 AD 12x，根据平行四边形的面积公式即可列出方程求解【解答】解：设 AC 交 AB于 H，AHCD，ACCA，四边形 AHCD 是平行四边形，A45，D90AHA 是等腰直角三角形设 AAx，则阴影部分的底长为 x，高 AD 12xx（12x）32第 17 页（共 28 页）x4 或 8，即
27、AA4 或 8cm故答案为：4 或 8【点评】考查了平移的性质及一元二次方程的解法等知识，解决本题关键是抓住平移后图形的特点，利用方程方法解题20 （3 分）如图，AD 和 BE 分别为三角形 ABC 的中线和角平分线，ADBE ，若ADBE4，则 AC 的长 3 【分析】过 D 点作 DFBE ，则 DF BE，F 为 EC 中点，在 RtADF 中求出 AF 的长度，根据已知条件易知 G 为 AD 中点，因此 E 为 AF 中点，则 AC AF【解答】解：过 D 点作 DFBE，如图所示：AD 是ABC 的中线，AD BE，F 为 EC 中点，ADDF ，ADBE4，则 DF2，AF 2
28、，BE 是ABC 的角平分线，AD BE ，ABGDBG，G 为 AD 中点，E 为 AF 中点，AC AF 3 故答案为：3 第 18 页（共 28 页）【点评】本题考查了三角形中位线定理、三角形中线和角平分线的性质以及勾股定理的应用，作出辅助线构建直角三角形是解题的关键三、解答题（共 60 分，其中 21、22 题各 7 分，23、24 题各 8 分，25、26、27 题各 10 分）21 （7 分）先化简，再求代数式 （x2y ）的值，其中 xtan60，y2sin30 【分析】先根据分式混合运算的法则把原式进行化简，再把 x3 代入进行计算即可；【解答】解：原式 ，xtan60 ，y
29、2sin302 1，原式 【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键22 （7 分）如图，在每个小正方形的边长均为 1 的方格纸中，线段 AB 的端点 A、B 均在小正方形的顶点上（1）在方格纸中画出以 AB 为一条直角边的等腰直角ABC，顶点 C 在小正方形的顶点上；（2）在方格纸中画出ABC 的中线 BD，将线段 DC 绕点 C 顺时针旋转 90得到线段CD，画出旋转后的线段 CD，连接 BD，直接写出四边形 BDCD的面积第 19 页（共 28 页）【分析】 （1）直接利用等腰直角三角形的性质得出 C 点位置；（2）直接利用三角形中线的定义以及结合网格直接
30、得出四边形 BDCD的面积【解答】解：（1）如图所示：ABC 即为所求；（2）如图所示：CD即为所求，四边形 BDCD的面积为： 10【点评】此题主要考查了旋转变换以及等腰直角三角形的性质，正确得出对应点位置是解题关键23 （8 分）某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取了本校部分学生进行问卷调查（必选且只选一类节目） ，将调查结果进行整理后，绘制了如下不完整的条形统计图和扇形统计图，其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的 3 倍还多 1 人请根据所给信息解答下列问题：（1）求本次抽取的学生人数（2）补全条形图，在扇形统计图中的横线上填上正
31、确的数值，并直接写出“体育”对应的扇形圆心角的度数（3）该校有 3000 名学生，求该校喜爱娱乐节目的学生大约有多少人？第 20 页（共 28 页）【分析】 （1）先求出喜爱体育节目的学生人数，再将喜爱五类电视节目的人数相加，即可得出本次抽取的学生人数；（2）由（1）中求出的喜爱体育节目的学生人数可补全条形图；用喜爱 C 类电视节目的人数除以总人数，可得喜爱 C 类电视节目的百分比，从而将扇形图补全；用 360乘以“体育”对应的百分比，可得“体育”对应的扇形圆心角的度数；（3）利用样本估计总体的思想，用 3000 乘以样本中喜爱娱乐节目的百分比即可得出该校 3000 名学生中喜爱娱乐节目的学生
32、人数【解答】解：（1）由条形图可知，喜爱戏曲节目的学生有 3 人，喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的 3 倍还多 1 人，喜爱体育节目的学生有：33+110 人，本次抽取的学生有：4+10+15+18+350 人；（2）喜爱 C 类电视节目的百分比为： 100%30%，“体育”对应的扇形圆心角的度数为：360 72补全统计图如下：（3）喜爱娱乐节目的百分比为： 100%36% ，该校 3000 名学生中喜爱娱乐节目的学生有：300036%1080 人【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表
33、示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小24 （8 分）如图，在 RtABC 中，BAC90，D 是 BC 的中点，连接 AD，E 为 AD 的中点，过 A 作 AFBC 交 BE 延长线于 F，连接 CF第 21 页（共 28 页）（1）求证：四边形 ADCF 是菱形；（2）在不添加任何辅助线的情况下，请直接写出与ACD 面积相等的三角形（不包含ACD） 【分析】 （1）首先根据题意画出图形，由 E 是 AD 的中点，AFBC，易证得AFE DBE，即可得 AFBD，又由在 RtABC 中，BAC90，D 是 BC 的中点，可得 ADBD CDAF ，证得四边形 ADCF
34、 是平行四边形，继而判定四边形 ADCF 是菱形；（2）根据等高模型即可解决问题；【解答】 （1）证明：如图，AFBC，AFE DBE，E 是 AD 的中点， AD 是 BC 边上的中线，AEDE ，BDCD，在AFE 和DBE 中，AFE DBE（AAS ） ；AFDB DBDC，AFCD，四边形 ADCF 是平行四边形，BAC90，D 是 BC 的中点，ADDC BC，四边形 ADCF 是菱形；（2）与ACD 面积相等的三角形有：ABD，ACF，AFB第 22 页（共 28 页）【点评】此题考查了菱形的判定与性质、全等三角形的判定与性质、等高模型等知识，解题的关键是正确寻找全等三角形解决问
35、题，属于中考常考题型25 （10 分）我市城市绿化工程招标，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要 60 天，若由甲队先做 20 天，再由甲、乙合作 12 天，共完成总工作量的三分之二（1）乙队单独完成这项工程需要多少天？（2）甲队施工 1 天需付工程款 4.5 万元，乙队施工一天需付工程款 2 万元，该工程由甲乙两队合作若干天后，再由乙队完成剩余工作，若要求完成此项工程的工程款不超过186 万元，求甲、乙两队最多合作多少天？【分析】 （1）设乙队单独完成这项工程需要 x 天，根据甲队完成的工作量+乙队完成的工作量总工作量的三分之二，即可得出关于 x 的分式方程，解之经检验后
36、即可得出结论；（2）设甲、乙两队合作 m 天，则乙队还需单独工作 （1 ） 天才可完工，根据总工程款4.5甲队工作时间+2乙队工作时间结合工程款不超过 186 万元，即可得出关于 m 的一元一次不等式，解之取其最大值即可得出结论【解答】解：（1）设乙队单独完成这项工程需要 x 天，依题意，得： + ，解得：x90，经检验，x90 是原方程的解，且符合题意答：乙队单独完成这项工程需要 90 天（2）设甲、乙两队合作 m 天，则乙队还需单独工作 （1 ） 天才可完工，依题意，得：4.5m+2m+（1 ） 186，整理，得：1.5m+180 186，解得：m4第 23 页（共 28 页）答：甲、乙两
37、队最多合作 4 天【点评】本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）根据各数量之间的关系，正确列出一元一次不等式26 （10 分）如图 1，ABC 为O 的内接三角形，AD 为O 的直径，AD 与 BC 相交于点F，DE 为 O 的切线，交 AC 的延长线于 E（1）求证：EB；（2）如图 2，若CFD3DAE，求证：ACBC ；（3）如图 3，在（2）的条件下，过点 A 作 AGBC 于点 G，AG 的延长线交 BD 于点H，点 H 为 BD 的中点若 CE1，求 FG 的长【分析】 （1）连接 BD，根据圆周角定理得到 AB
38、D90 ，根据切线的性质得到ADE90，等量代换即可证明；（2）连接 OB、OC，根据三角形的外角的性质、等腰三角形的性质证明CBACAB，根据等腰三角形的判定定理解答；（3）作 OM BC 于 M，DNBC 于 N，连接 CD，根据垂径定理得到 BMMC，根据正切的定义得到 AG5GH，根据相似三角形的性质计算即可【解答】 （1）证明：如图 1，连接 BD，AD 为 O 的直径，ABD90，即ABC +CBD90，AD 为 O 的直径，DE 为O 的切线，ADE90，即DAE +E90，CBDDAE，EB ；（2）证明：如图 2，连接 OB、OC，第 24 页（共 28 页）CFD3DAE，
39、CFDACF+DAE，ACF2DAE，OAOC，OACOCA，OACOCAOCB，OBOC，OBCOCB，OBCOAC，OAOB ，OBAOAB，CBACAB，ACBC；（3）如图 3，作 OMBC 于 M，DNBC 于 N，连接 CD，OM BC，BMCM，AGOM DN，OA OD，GM MN，GHDN，BHHD，BGGN，设 MG MN a，则 BGGN2a，CG4a，BC6a，由（2）得，ACBC6a，AG 2 a，tanBAG ，HBG BAG， ，AG5GH ，DN2GH，AGDN，第 25 页（共 28 页） ，同理可得，AC CD，CD CE，CBCA5，GN BC ，GF G
40、N 【点评】本题考查的是圆的知识的综合运用，掌握圆周角定理、切线的性质定理、勾股定理、锐角三角函数的定义是解题的关键27 （10 分）在平面直角坐标系中，O 为坐标原点，抛物线 yax 2+c 交 x 轴于点 A、B（A左 B 右） ，交 y 轴于点 C，OBOC，且 SABC 4（1）如图 1，求 a、c 的值；（2）如图 2，点 P 在第三象限的抛物线上，BP 交 y 轴于点 D，设点 P 的横坐标为 t，线段 CD 的长为 d，求 d 与 t 之间的函数关系式，并直接写出自变量 t 的取值范围；第 26 页（共 28 页）（3）如图 3，在（2）的条件下，点 Q 在线段 PD 上，若PC
41、 CQ，2PCDPCQ 45，求点 P 的坐标【分析】 （1）根据三角形的面积公式求出 B、C 两点坐标，代入抛物线解析式解方程组即可解决问题（2）设直线 PB 解析式为 ykx+b，把 P（t ， t2+2） ，B（2，0）代入，解方程组即可（3）如图 2 中，作 P 关于 y 轴的对称点 P，连接 CP，PP，QP，PP交 y 轴于 F，PQ 与 OF 交于点 E，作 PQCQ 于 Q只要证明OBD 45，求出直线 PB 的解析式，解方程组即可解决问题【解答】解：（1）如图 1 中，设 OBOCOA m， 2mm4，m2，点 B 坐标（2，0） ，C（0， 2） ，代入抛物线解析式得到解得
42、 （2）如图 1 中，第 27 页（共 28 页）设直线 PB 解析式为 ykx+ b，把 P（t ， t2+2） ，B（2，0）代入得解得 ，直线 PB 的解析式为 y x+t+2，点 D 的坐标为 t+2，dt （t2） （3）如图 2 中，作 P 关于 y 轴的对称点 P，连接 CP，PP，QP，PP交 y 轴于 F，PQ 与 OF 交于点 E，作 PQCQ 于 Q根据对称性可知：PCDPCD，PC CP ，PC CQ，2PCD PCQ45，PCQ45，CP CQ，Q 与 Q重合，CQP是等腰直角三角形，CQEEFP90，CEQFEP，第 28 页（共 28 页）DCQFPQ，CDPF FP （由 2 可知） ，CDQPFQ，DQQF ， CQDPQF，DQF CQP 90，DQF 是等腰直角三角形，QDF ODBOBD45，直线 BD 的解析式为 yx2，由 解得 或 ，点 P 坐标为（4，6） 【点评】本题考查考查二次函数的综合题、待定系数法、全等三角形的判定和性质、一次函数等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，利用数形结合的思想思考问题，属于中考压轴题
