1、山东省济南市历下区 2017-2018 学年七年级第二学期期末数学试卷一、选择题（本大题共 12 个小题，每小题 4 分，共 48 分）14 的算术平方根（ ）A2 B2 C D2下列交通标志是轴对称图形的是（ ）A BC D3下列事件为必然事件的是（ ）A小王参加本次数学考试，成绩是 150 分B打开电视机，CCTV 第一套节目正在播放新闻C某设计运动射靶一次，正中靶心D口袋中装有 2 个红球和 1 个白球，从中摸出 2 个球，其中必有红球4如图，小聪把一块含有 60角的直角三角板的两个顶点放在直尺的对边上，并测得125，则2 的度数是（ ）A15 B25 C35 D455在下列各数中是无理
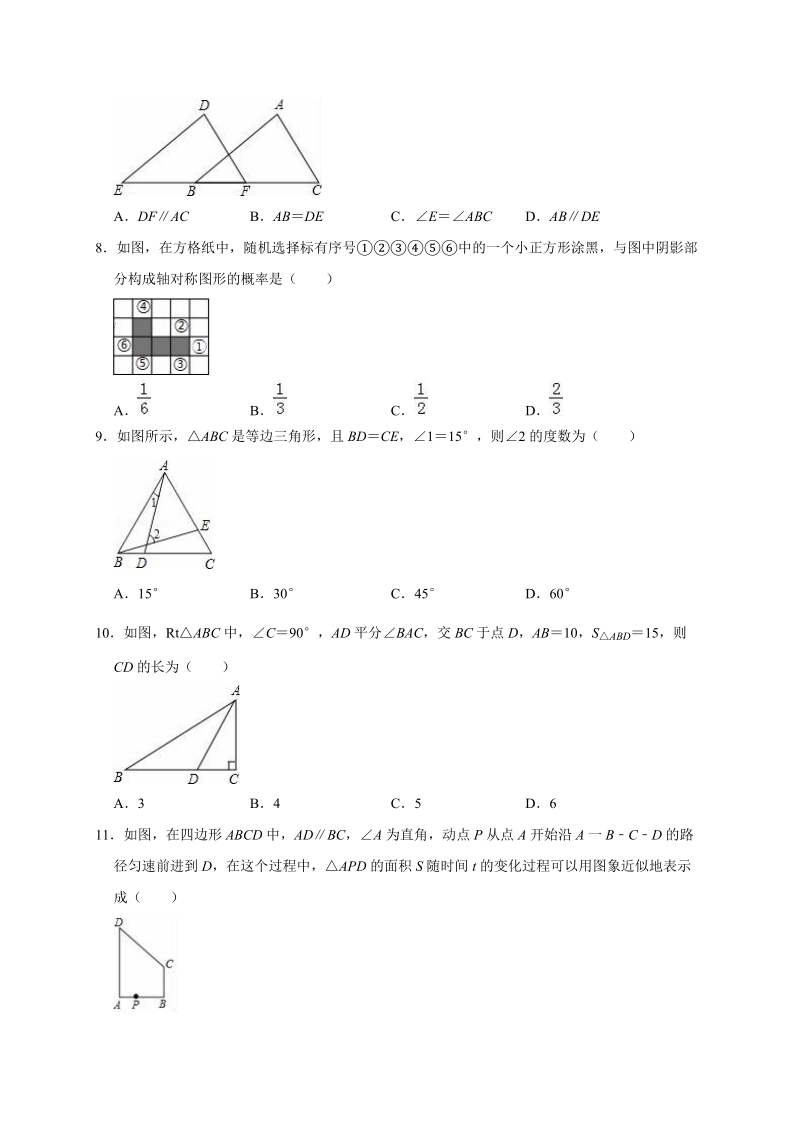
2、数的有（ ）， ， ，2，3.14，2.0101010（相邻两个 1 之间有 1 个 0）A2 个 B3 个 C4 个 D5 个6若等腰三角形的两边长为 3 和 7，则该等腰三角形的周长为（ ）A10 B13 C17 D13 或 177如图，E、B、F 、C 四点在一条直线上，且 EBCF ，AD，增加下列条件中的一个仍不能证明ABCDEF ，这个条件是（ ）ADFAC BABDE CEABC DAB DE8如图，在方格纸中，随机选择标有序号中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（ ）A B C D9如图所示，ABC 是等边三角形，且 BDCE，115，则2 的度数为（ ）
3、A15 B30 C45 D6010如图，Rt ABC 中，C90，AD 平分BAC，交 BC 于点 D，AB10，S ABD 15，则CD 的长为（ ）A3 B4 C5 D611如图，在四边形 ABCD 中，ADBC，A 为直角，动点 P 从点 A 开始沿 A 一 BCD 的路径匀速前进到 D，在这个过程中， APD 的面积 S 随时间 t 的变化过程可以用图象近似地表示成（ ）A BC D12如图，弹性小球从点 P 出发，沿所示方向运动，每当小球碰到长方形的边时反弹，反弹时反射角等于入射角当小球第 1 次碰到长方形的边时的点为 Q，第 2 次碰到矩形的边时的点为M，第 2018 次碰到矩形的
4、边时的点为图中的（ ）AP 点 BQ 点 CM 点 DN 点二、填空题（本大题共 6 小题，每小题 4 分，共 24 分）13比较大小： 514等腰三角形的一个角是 80，则它的底角是 15将一个小球在如图所示的地撰上自由滚动，最终停在黑色方砖上的概率为 16如图，ABC 的两边 AC 和 BC 的垂直平分极分别交 AB 于 D、E 两点，若 AB 边的长为10cm，则CDE 的周长为 cm17如图，在ABC 中，ABC 与ACB 的平分线相交于点 O，过点 O 作 DEBC，分别交AB、 AC 于点 D、E ，若 AB6，AC5，则ADE 的周长是 18甲、乙两人在直线道路上同起点、同终点、
5、同方向，分别以不同的速度匀速跑步 1000 米，先到终点的人原地休息，已知甲先出发 30 秒后，乙才出发，在跑步的整个过程中，甲、乙两人的距离 y（米）与甲出发的时间 x（秒）之间的关系如图所示，则乙到达终点时甲距离终点的距离是 米三、解答题（本大题共 7 小题，共 78 分）19（18 分）化简与计算：（1） ；（2） ；（3） ；（4） 4 ；（5）（ + ）（ ）；（6）（2 +1） 220（8 分）如图，在所给的方格图中，完成下列各题（用直尺画图，保留作图痕迹）（1）画出格点ABC 关于直线 DE 对称的A 1B1C1；（2）求ABC 的面积；（3）在 DE 上面出点 P，使 PA+P
6、C 最小21（8 分）如图，点 B、F、C 、E 在直线 l 上（F、C 之间不能直接测量），点 A、D 在 l 异侧，AB DE，AD，测得 ABDE （1）求证：ABCDEF；（2）若 BE10m，BF 3m，求 FC 的长度22（10 分）一个不透明的布袋里装有 10 个球，其中 2 个红球，3 个白球，5 个黄球，它们除颜色外其余都相同（1）求摸出 1 个球是白球的概率；（2）摸到哪种颜色的球的概率最大？并说明理由；23（10 分）“十一”期间，小明和父母一起开车到距家 200 千米的景点旅游，出发前，汽车油箱内储油 45 升，当行驶 150 千米时，发现油箱油箱余油量为 30 升（假
7、设行驶过程中汽车的耗油量是均匀的）（1）求该车平均每千米的耗油量，并写出行驶路程 x（千米）与剩余油量 Q（升）的关系式；（2）当 x280（千米）时，求剩余油量 Q 的值；（3）当油箱中剩余油量低于 3 升时，汽车将自动报警，如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由24（12 分）在ABC 中，ABAC （1）如图 1，如果BAD30，AD 是 BC 上的高，ADAE ，则EDC （2）如图 2，如果BAD40，AD 是 BC 上的高，ADAE ，则EDC （3）思考：通过以上两题，你发现BAD 与EDC 之间有什么关系？请用式子表示： （4）如图 3，如果 AD 不是 B
8、C 上的高，ADAE，是否仍有上述关系？如有，请你写出来，并说明理由25（12 分）如图 1，点 C 为线段 AB 上任意一点（不与点 A、B 重合），分别以 AC、BC 为一腰在 AB 的同侧作等腰 ACD 和BCE，CA CD，CB CE，ACDBCE30，连接 AE交 CD 于点 M，连接 BD 交 CE 于点 N，AE 与 BD 交于点 P，连接 CP（1）线段 AE 与 DB 的数量关系为 ；请直接写出APD ；（2）将BCE 绕点 C 旋转到如图 2 所示的位置，其他条件不变，探究线段 AE 与 DB 的数量关系，并说明理由；求出此时APD 的度数；（3）在（2）的条件下求证：AP
9、CBPC 附加题（共 3 个小题，第 l、 2 小题 5 分，第 3 题 10 分）26（5 分）如图，直角梯形 ABCD 中，动点 P 从 B 点出发，由 BCDA 沿梯形的边运动，设点 P 运动的路程为 x，ABP 的面积为 y，函数图象如图 所示，则直角梯形 ABCD 的面积为 27（5 分）如图，ABC 中，D 是 AB 的中点，DEAB，ACE +BCE180，EFAC 交AC 于 F，AC12，BC8，则 AF 28（10 分）已知：2x ，求 的值参考答案一、选择题1A2C3D4C 5A6C 7B8C9D10A11B 12C 二、填空题131450或 80151610cm1711
10、18195三、解答题19解：（1） 2；（2） 422；（3）7；（4） 44 5 4 2 ；（5）（ + ）（ ）321；（6）（2 +1） 220+1+421+4 20解：（1）如图所示：A 1B1C1，即为所求；（2）ABC 的面积为：23 22 11 132；（3）如图所示：点 P 即为所求21（1）证明：ABDE ，ABCDEF，在ABC 与DEF 中，ABCDEF；（2）ABCDEF，BCEF，BF+FCEC+FC，BFEC，BE10m，BF3m，FC10334m22解：（1）袋子中共有 10 个球，其中白球有 3 个，摸出 1 个球是白球的概率 ；（2）摸到黄色球的概率最大，因为
11、袋子中黄色球的个数最多23解：（1）该车平均每千米的耗油量为（4530）1500.1（升/千米），行驶路程 x（千米）与剩余油量 Q（升）的关系式为 Q450.1x；（2）当 x280 时，Q 450.128017（L）答：当 x280（千米）时，剩余油量 Q 的值为 17L（3）（453）0.1420（千米），420400，他们能在汽车报警前回到家24解：（1）在ABC 中，ABAC ，AD 是 BC 上的高，BADCAD，BAD30，BADCAD30，ADAE，ADEAED75，EDC15（2）在ABC 中，AB AC ，AD 是 BC 上的高，BADCAD，BAD40，BADCAD40，
12、ADAE，ADEAED70，EDC20（3）BAD2EDC（或EDC BAD）（4）仍成立，理由如下ADAE，ADEAED，BAD+BADCADE+EDCAED+EDC（EDC+C）+EDC2EDC+C又ABAC，BCBAD2EDC故分别填 15，20，EDC BAD25（1）解：如图 1 中，ACDBCE，ACD+DCEBCE+ DCE，ACEDCB，又CACD，CECB，ACEDCBAEBD ，CAECDB，AMCDMP，APDACD30，故答案为 AEBD ，30（2）解：如图 2 中，结论：AEBD，APD30理由：ACDBCE，ACD+DCEBCE+ DCE，ACEDCB，又CACD
13、，CECB，ACEDCBAEBD ，CAECDB，AMP DMC，APDACD30（3）证明：如图 21 中，分别过 C 作 CHAE，垂足为 H，过点 C 作 CGBD，垂足为 G，ACEDCBAEBD ，S ACE S DCB （全等三角形的面积相等），CHCG ，DPCEPC（角平分线的性质定理的逆定理），APDBPE，APCBPC附加题26解：动点 P 从 B 点出发，由 BC DA 沿梯形的边运动；当运动到线段 CD 上时，三角形的面积的值开始固定由图象可以看出，x 为 4 时，面积开始不变，所以 BC 为 4；x 为 9 时，面积不变结束，所以 CD945；那么 AD1495，AB CD+ 5+ 8；直角梯形 ABCD 的面积为 （5+8）42627解：连接 AE，BE ，过 E 作 EGBC 于 G，D 是 AB 的中点， DEAB，DE 垂直平分 AB，AEBE，ACE+ BCE180，ECG+BCE 180，ACEECG，又EFAC， EGBC，EFEG ，FECGEC，CFEF，CGEG，CFCG，在 Rt AEF 和 RtBEG 中，RtAEFRtBEG（HL ），AFBG ，设 CFCGx ，则 AFAC CF12x，BGBC +CG8+x，12x8+x，解得 x2，AF12210故答案为：1028解：2x ，x ，1x 21 （ ） 2 ， +
