 2019年初升高数学衔接之方程与不等式
2019年初升高数学衔接之方程与不等式
《2019年初升高数学衔接之方程与不等式》由会员分享,可在线阅读,更多相关《2019年初升高数学衔接之方程与不等式(21页珍藏版)》请在七七文库上搜索。
1、07 方程与不等式高中必备知识点 1:二元二次方程组的解法方程 2260xyxy是一个含有两个未知数,并且含有未知数的项的最高次数是 2 的整式方程,这样的方程叫做二元二次方程其中 2, , 2叫做这个方程的二次项, x, y叫做一次项,6 叫做常数项我们看下面的两个方程组: 24310,;xy220,56.xy第一个方程组是由一个二元二次方程和一个二元一次方程组成的,第二个方程组是由两个二元二次方程组成的,像这样的方程组叫做二元二次方程组下面我们主要来研究由一个二元二次方程和一个二元一次方程组成的方程组的解法一个二元二次方程和一个二元一次方程组成的方程组一般可以用代入消元法来解典型考题【典型
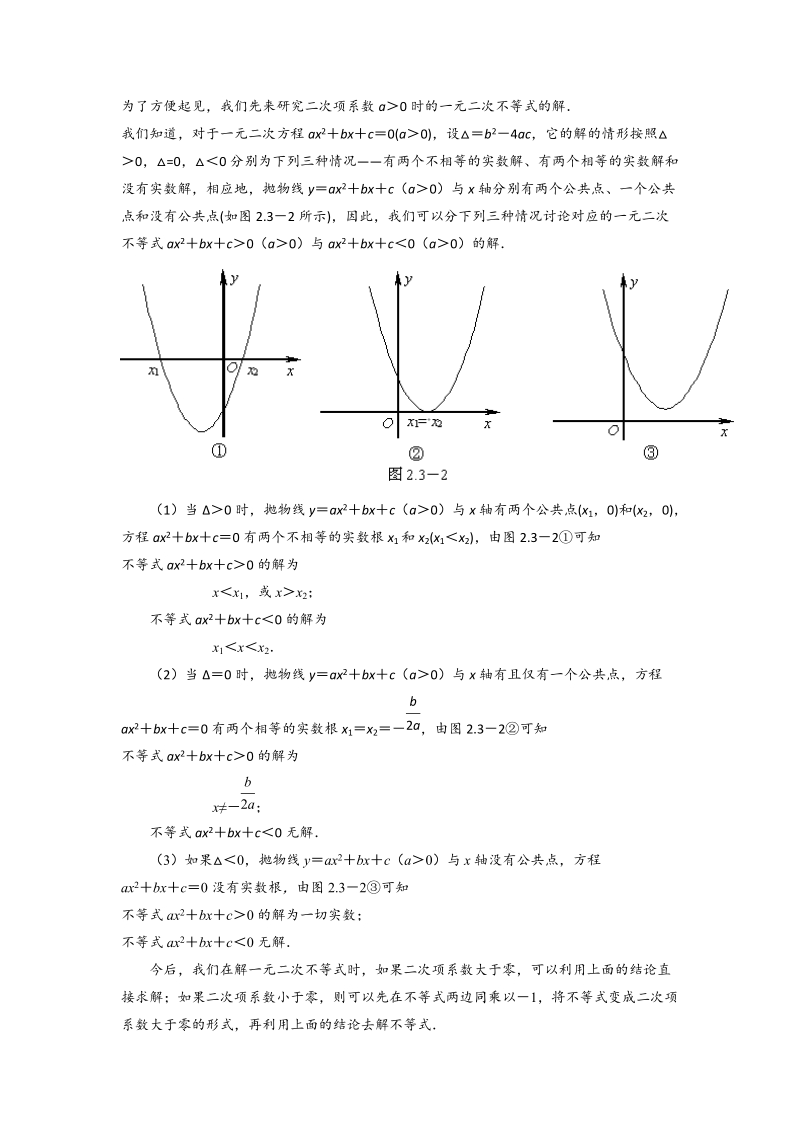
2、例题】已知方程组 有两组相等的实数解,求 的值,并求出此时方程组的解 .2+226=0=+3 【变式训练】解方程组: 222=0,2+2+2=1, 【能力提升】解方程组:高中必备知识点 2:一元二次不等式的解法为了方便起见,我们先来研究二次项系数 a0 时的一元二次不等式的解我们知道,对于一元二次方程 ax2bxc0(a0),设b 24ac,它的解的情形按照0 , =0,0 分别为下列三种情况 有两个不相等的实数解、有两个相等的实数解和没有实数解,相应地,抛物线 yax 2bxc(a0)与 x 轴分别有两个公共点、一个公共点和没有公共点(如图 2.32 所示) ,因此,我们可以分下列三种情况讨
3、论对应的一元二次不等式 ax2bxc0(a0)与 ax2bxc0(a0 )的解(1)当 0 时,抛物线 yax 2bxc(a0)与 x 轴有两个公共点( x1,0)和(x 2,0) ,方程 ax2bxc0 有两个不相等的实数根 x1 和 x2(x1x 2),由图 2.32可知不等式 ax2bxc0 的解为xx 1,或 x x2;不等式 ax2bxc0 的解为x1x x 2(2)当 0 时,抛物线 yax 2bxc(a0)与 x 轴有且仅有一个公共点,方程ax2bxc0 有两个相等的实数根 x1x 2 ,由图 2.32可知b2a不等式 ax2bxc0 的解为x ;b2a不等式 ax2bxc0 无
4、解(3)如果0,抛物线 yax 2bxc(a0)与 x 轴没有公共点,方程ax2bxc0 没有实数根 , 由图 2.32可知不等式 ax2bxc 0 的解为一切实数;不等式 ax2bxc 0 无解今后,我们在解一元二次不等式时,如果二次项系数大于零,可以利用上面的结论直接求解;如果二次项系数小于零,则可以先在不等式两边同乘以1,将不等式变成二次项系数大于零的形式,再利用上面的结论去解不等式(1 )典型考题【典型例题】解下列不等式:(1)3x 22 x 80;(2)0x 2x24 ;【变式训练】求不等式 260x的解【能力提升】解下列不等式:(1) 062x;(2) 1;(3) ()4x专题验收
5、测试题1不等式组 31 x的解集在数轴上表示正确的是( )A BC D2 20 位同学在植树节这天共种了 52 棵树苗,其中男生每人种 3 棵,女生每人种 2 棵,设男生有 x 人,女生有 y 人,根据题意,列方程组正确的是( )A B+=523+2=20 +=522+3=20 C D+=202+3=52 +=203+2=52 3解不等式 ,解题依据错误的是( )解:去分母,得 5(x+2) 3(2x1 )去括号,得 5x+106x3移项,得 5x6x 31 0合并同类项,得x 13系数化 1,得 x13A去括号法则 B 不等式的基本性质 1C 合并同类项法则 D 不等式的基本性质 24已知温
6、州至杭州铁路长为 380 千米,从温州到杭州乘“G”列动车比乘“ D”列动车少用 20分钟, “G”列动车比“D” 列动车每小时多行驶 30 千米,设“G”列动车速度为每小时 x 千米,则可列方程为( )A3802xB38020xC13D135不等式组(2)45x的整数解有( )A3 个 B4 个 C5 个 D6 个6方程组 的实数解的个数是( )422=032+2+6=0 A4 B2 C1 D07 以下说法:关于 x 的方程 的解是 x=c(c 0) ; +1=+1方程组 正整数的解有 2 组; +=63+=23已知关于 x,y 的方程组 ,其中3a1 ,当 a=1 时,方程组的解也是方程
7、x+y=4a 的解;其中正确的有( )A B C D8二元二次方程组 的解是A BC D9一元二次方程 kx2+4x+10 有两个实数根,则 k 的取值范围是( )Ak4 Bk 4 Ck 4 Dk4 且 k010一元二次方程(x 1) (x +5)3x+2 的根的情况是( )A方程没有实数根B方程有两个相等的实数根C方程有两个不相等的实数根D方程的根是 1、 5 和11不等式组 有 3 个整数解,则 m 的取值范围是_103(2)=4 14关于 x 的一元二次方程 x22x+m10 有两个实数根,则 m 的取值范围是_15方程 x2+2x0 的解为_16设 是方程 的两个实数根,则 的值为_2
8、2019=017已知关于 的一元二次方程 ,其中 为常数. 2+(5)+1=0 (1 )求证:无论 为何值,方程总有两个不相等实数根;(2 )若抛物线 轴交于 两点,且 ,|12|=4求 的值;18 ( 1)用配方法解方程:x 2-2x-2=0;(2)已知关于 x 的方程(m-2)x 2+(m-2)x-1=0 有两个相等的实数根,求 m 的值19已知关于 x 一元二次方程 ,24+=0(1)当 时,试解这个方程;=1(2)若方程的两个实数根为 ,且 ,求 的值.12212+22=0 20某学校准备采购一批茶艺耗材和陶艺耗材.经查询,如果按照标价购买两种耗材,当购买茶艺耗材的数量是陶艺耗材数量的
9、 2 倍时,购买茶艺耗材共需要 18000 元,购买陶艺耗材共需要 12000 元,且一套陶艺耗材单价比一套茶艺耗材单价贵 150 元.(1 )求一套茶艺耗材、一套陶艺耗材的标价分别是多少元?(2 )学校计划购买相同数量的茶艺耗材和陶艺耗材.商家告知,因为周年庆,茶艺耗材的单价在标价的基础上降价 2 元,陶艺素材的单价在标价的基础降价 150 元,该校决定增加采购数量,实际购买茶艺素材和陶艺素材的数量在原计划基础上分别增加了 2.5 %和,结果在结算时发现,两种耗材的总价相等,求 的值 .21某市举行“行动起来,对抗雾霾” 为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、
10、乙两种树共 50 棵,已知甲树每棵 800 元,乙树每棵 1200 元(1 )若购买两种树的总金额为 56000 元,求甲、乙两种树各购买了多少棵?(2 )若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?22解不等式213x1,并把它的解集表示在数轴上专题 07 方程与不等式高中必备知识点 1:二元二次方程组的解法方程 2260xyxy是一个含有两个未知数,并且含有未知数的项的最高次数是 2 的整式方程,这样的方程叫做二元二次方程其中 2, , 2叫做这个方程的二次项, x, y叫做一次项,6 叫做常数项我们看下面的两个方程组:24310,;xy220,56.xy第一个方程组是由一
11、个二元二次方程和一个二元一次方程组成的,第二个方程组是由两个二元二次方程组成的,像这样的方程组叫做二元二次方程组下面我们主要来研究由一个二元二次方程和一个二元一次方程组成的方程组的解法一个二元二次方程和一个二元一次方程组成的方程组一般可以用代入消元法来解典型考题【典型例题】已知方程组 有两组相等的实数解,求 的值,并求出此时方程组的解 .2+226=0=+3 【答案】 ,当 时 ;当 时 =卤 1 =1 =2=1 =1 =2=1 【解析】把代入后计算得 ,(22+1)2+12+12=0方程组有两组相等的实数解,(12m) 24(2m 2+1)120 ,解得: ,=卤 1当 时,解得=1 =2=
12、1 当 时,解得=1 =2=1 【变式训练】解方程组: 222=0,2+2+2=1, 【答案】1=231=13 ; 2=232=13 【解析】,由得 (x+y) (x-2y)=0,x+y=0 或 x-2y=0,由得 (x+y) 2=1,x+y=1 或 x+y=-1,所以原方程组化为 ,所以原方程组的解为 1=231=13 2=232=13 【能力提升】解方程组:【答案】 1=81=4 ,2=22=2 【解析】由得: (+2)()=0所以 ,.高中必备知识点 2:一元二次不等式的解法为了方便起见,我们先来研究二次项系数 a0 时的一元二次不等式的解我们知道,对于一元二次方程 ax2bxc0(a0
13、),设b 24ac,它的解的情形按照0 , =0,0 分别为下列三种情况 有两个不相等的实数解、有两个相等的实数解和没有实数解,相应地,抛物线 yax 2bxc(a0)与 x 轴分别有两个公共点、一个公共点和没有公共点(如图 2.32 所示) ,因此,我们可以分下列三种情况讨论对应的一元二次不等式 ax2bxc0(a0)与 ax2bxc0(a0 )的解(1)当 0 时,抛物线 yax 2bxc(a0)与 x 轴有两个公共点( x1,0)和(x 2,0) ,方程 ax2bxc0 有两个不相等的实数根 x1 和 x2(x1x 2),由图 2.32可知不等式 ax2bxc0 的解为xx 1,或 x


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2019 年初 升高 数学 衔接 方程 不等式
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-70023.html