1、2019年上海市徐汇区高考数学一模试卷一、填空题（本大题共有 12 题，满分 54 分，第 1-6 题每题 4 分，第 7-12 题每题 5 分）考生应在答题纸的相应位置直接填写结果.1 （4 分）若复数 z 满足 iz 1+2i，其中 i 是虚数单位，则 z 的实部为 2 （4 分）已知全集 UR，集合 A y|yx 2 ，x R，x0，则 UA 3 （4 分）若实数 x，y 满足 xy1，则 2x2+y2 的最小值为 4 （4 分）若数列a n的通项公式为 an （n N*） ，则 an &n
2、bsp; 5 （4 分）已知双曲线 1（a0，b0）的一条渐近线方程是 y2x，它的一个焦点与抛物线 y220x 的焦点相同，则此双曲线的方程是 6 （4 分）在平面直角坐标系 xOy 中，直线经过坐标原点， （3，1）是 l 的一个法向量已知数列a n满足：对任意的正整数 n，点（a n+1，a n）均在 l 上，若 a26，则 a3的值为 7 （5 分）已知（2x 2 ） n（nN*）的展开式中各项的二项式系数之和为 128，则其展开式中含 项的系数是 （结果用数值表示）8 （5 分）上海市普通高中学业水平
3、等级考成绩共分为五等十一级，各等级换算成分数如表所示：等级 A+ A B+ B B C+ C C D+ D E分数 70 67 64 61 58 55 52 49 46 43 40上海某高中 2018 届高三（1）班选考物理学业水平等级考的学生中，有 5 人取得 A+成绩，其他人的成绩至少是 B 级及以上，平均分是 64 分，这个班级选考物理学业水平等级考的人数至少为 人9 （5 分）已知函数 f（x ）是以 2 为周期的偶函数，当 0x1 时，f（x）lg（x+1） ，令函数 g（x ） f（x ） （x 1，2） ，则 g（x）的反函数为 &nbs
4、p; 10 （5 分）已知函数 ysinx 的定义域是 a，b，值域是 1， ，则 ba 的最大值是 第 2 页（共 20 页）11 （5 分）已知 R，函数 f（x） ，若函数 f（x）恰有 2 个零点，则 的取值范围是 12 （5 分）已知圆 M：x 2+（ y1） 21，圆 N：x 2+（y +1） 21直线 l1、l 2 分别过圆心M、N ，且 11 与圆 M 相交于 A，B 两点，1 2 与圆 N 相交于 C，D 两点，点 P 是椭圆1 上任意一点，则 + 的最小值为 二、选择题（本大题
5、共有 4 题，满分 20 分，每题 5 分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.13 （5 分）设 R，则“ ”是“sin ”的（ ）A充分非必要条件 B必要非充分条件C充要条件 D既非充分也非必要条件14 （5 分）魏晋时期数学家刘徽在他的著作九章算术注中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖” ，刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为 ：4若正方体的棱长为 2，则“牟合方盖”的体积为（ ）A16 B16 C D15 （5 分）对于函数 yf（x） ，如果其图象上的任意一点
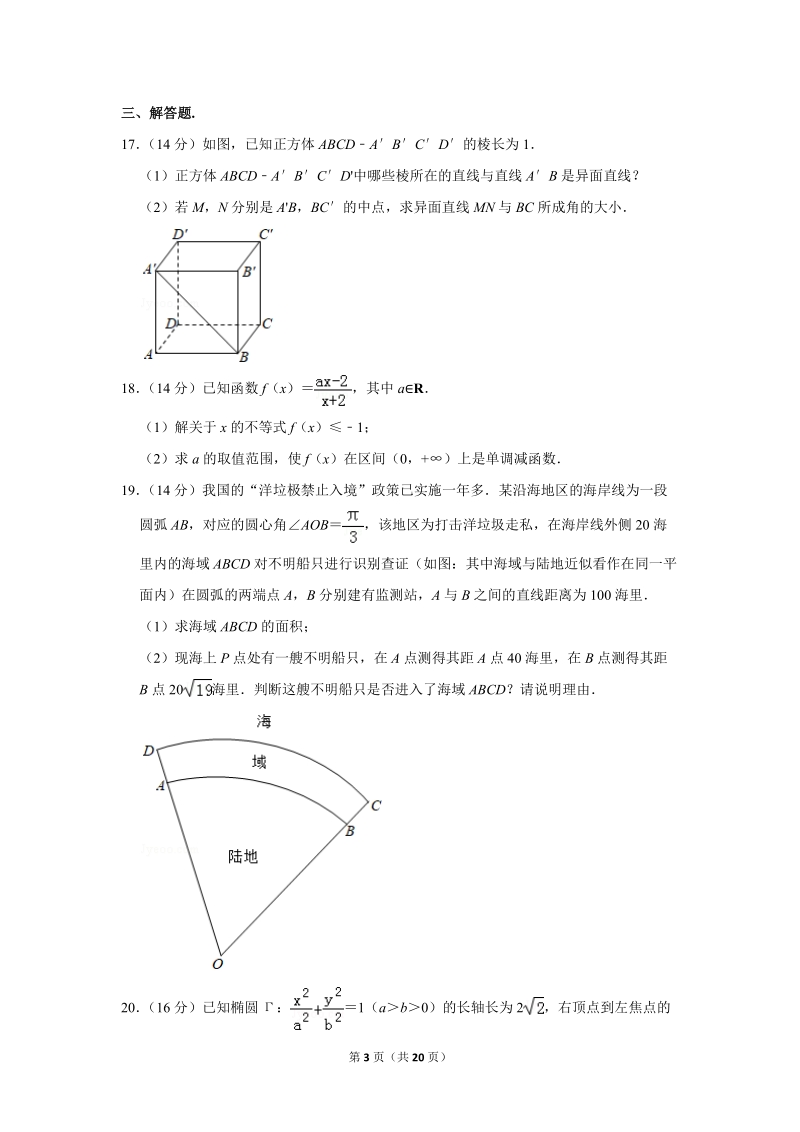
6、都在平面区域（x，y ）| （y+x）（yx ）0内，则称函数 f（x）为“蝶型函数” ，已知函数： ysinx；y，下列结论正确的是（ ）A、 均不是“蝶型函数”B、 均是 “蝶型函数”C是“蝶型函数” ；不是 “蝶型函数”D不是 “蝶型函数”：是“蝶型函数”16 （5 分）已知数列a n是公差不为 0 的等差数列，前 n 项和为 Sn，若对任意的 nN*，都有 SnS 3，则 的值不可能为（ ）A2 B C D第 3 页（共 20 页）三、解答题.17 （14 分）如图，已知正方体 ABCDABC D的棱长为 1（1）正方体 ABCDAB C D'中哪些棱所
7、在的直线与直线 AB 是异面直线？（2）若 M，N 分别是 A'B，BC的中点，求异面直线 MN 与 BC 所成角的大小18 （14 分）已知函数 f（x ） ，其中 aR（1）解关于 x 的不等式 f（x）1；（2）求 a 的取值范围，使 f（ x）在区间（0，+）上是单调减函数19 （14 分）我国的“洋垃极禁止入境”政策已实施一年多某沿海地区的海岸线为一段圆弧 AB，对应的圆心角 AOB ，该地区为打击洋垃圾走私，在海岸线外侧 20 海里内的海域 ABCD 对不明船只进行识别查证（如图：其中海域与陆地近似看作在同一平面内）在圆弧的两端点 A，B 分别建有监测站，A 与 B 之间的
8、直线距离为 100 海里（1）求海域 ABCD 的面积；（2）现海上 P 点处有一艘不明船只，在 A 点测得其距 A 点 40 海里，在 B 点测得其距B 点 20 海里判断这艘不明船只是否进入了海域 ABCD？请说明理由20 （16 分）已知椭圆 ： 1（ab0）的长轴长为 2 ，右顶点到左焦点的第 4 页（共 20 页）距离为 +1，直线 l：y kx+m 与椭圆 交于 A，B 两点（1）求椭圆 的方程；（2）若 A 为椭圆的上项点，M 为 AB 中点，O 为坐标原点，连接 OM 并延长交椭圆 于 N， ，求 k 的值（3）若原点 O 到直线 l 的距离为 1， ，当 时，求OAB 的面积
9、S 的范围21 （18 分）已知项数为 n0（n 04）项的有穷数列a n，若同时满足以下三个条件：a1 1，a m（m 为正整数） ； aia i1 0 或 1，其中 i2，3，n 0；任取数列 an中的两项 ap，a q（pq） ，剩下的 n02 项中一定存在两项as， at（s t） ，满足 ap+aqa s+at，则称数列 an为 数列（1）若数列a n是首项为 1，公差为 1，项数为 6 项的等差数列，判断数列 an是否是数列，并说明理由（2）当 m3 时，设 数列 an中 1 出现 d1 次，2 出现 d2 次，3 出现 d3 次，其中d1，d 2，d 3N*求证：d 14，d 2
10、2，d 34；（3）当 m2019 时，求 数列 an中项数 n0 的最小值第 5 页（共 20 页）2019 年上海市徐汇区高考数学一模试卷参考答案与试题解析一、填空题（本大题共有 12 题，满分 54 分，第 1-6 题每题 4 分，第 7-12 题每题 5 分）考生应在答题纸的相应位置直接填写结果.1 （4 分）若复数 z 满足 iz 1+2i，其中 i 是虚数单位，则 z 的实部为 2 【分析】把已知等式变形，再由复数代数形式的乘除运算化简得答案【解答】解：由 iz1+2i，得 z ，z 的实部为 2故答案为：2【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题2 （
11、4 分）已知全集 UR，集合 A y|yx 2 ，x R，x0，则 UA （，0 【分析】可解出集合 A，然后进行补集的运算即可【解答】解：A（0，+） ； UA（，0故答案为：（，0【点评】考查描述法、区间表示集合的定义，以及补集的运算3 （4 分）若实数 x，y 满足 xy1，则 2x2+y2 的最小值为 2 【分析】根据基本不等式可得【解答】解：xy1，2x 2+y22 2 ， （当且仅当 2xy 时，取等） ，故答案为：2 【点评】本题考查了基本不等式及其应用属基础题4 （4 分）若数列a n的通项公式为 an （n N*） ，则 an 1 【分析】利用行列式求出数列的通
12、项公式，然后利用数列的极限求解即可【解答】解：数列a n的通项公式为 an ，第 6 页（共 20 页）则 an （ ）1故答案为：1【点评】本题考查数列的极限的求法，通项公式的求法，考查计算能力5 （4 分）已知双曲线 1（a0，b0）的一条渐近线方程是 y2x，它的一个焦点与抛物线 y220x 的焦点相同，则此双曲线的方程是 【分析】求得抛物线的焦点，可得双曲线的焦点位置，求出渐近线方程，可得双曲线的a，b，解方程即可得到所求双曲线的方程【解答】解：抛物线 y220x 的焦点为（5，0） ，则双曲线的焦点在 x 轴上，双曲线 的一条渐近线为 y2x，可得 b2a，
13、由题意双曲线 的一个焦点与抛物线 y220x 的焦点相同，可得 5，解得 a ，b2 ，则双曲线的方程为： 故答案为： 【点评】本题考查双曲线的渐近线方程和焦点坐标，以及抛物线的焦点，考查运算能力，属于基础题6 （4 分）在平面直角坐标系 xOy 中，直线经过坐标原点， （3，1）是 l 的一个法向量已知数列a n满足：对任意的正整数 n，点（a n+1，a n）均在 l 上，若 a26，则 a3的值为 2 【分析】由直线的法向量可得直线的斜率和直线方程，求得 an+1 an，则数列a n为公比 q 为 的等比数列，运用等比数列的通项公式可得所求值第 7 页（共 20 页）【解答】解：直线经过
14、坐标原点， （3，1）是 l 的一个法向量，可得直线 l 的斜率为3，即有直线 l 的方程为 y3x，点（a n+1，a n）均在 l 上，可得 an3a n+1，即有 an+1 an，则数列a n为公比 q 为 的等比数列，可得 a3a 2q6（ ）2故答案为：2【点评】本题主要考查等比数列的定义和通项公式的运用，考查直线方程的求法，考查运算能力，属于基础题7 （5 分）已知（2x 2 ） n（nN*）的展开式中各项的二项式系数之和为 128，则其展开式中含 项的系数是 84 （结果用数值表示）【分析】由已知求得 n，写出二项展开式的通项，由 x 的指数为1 求得 r，则答案可求【解答】解：
15、由题意，2 n128，得 n7（2x 2 ） n（2x 2 ） 7，其二项展开式的通项 由 143r1，得 r5展开式中含 项的系数是 故答案为：84【点评】本题考查二项式定理，关键是熟记二项展开式的通项，是基础题8 （5 分）上海市普通高中学业水平等级考成绩共分为五等十一级，各等级换算成分数如表所示：等级 A+ A B+ B B C+ C C D+ D E分数 70 67 64 61 58 55 52 49 46 43 40上海某高中 2018 届高三（1）班选考物理学业水平等级考的学生中，有 5 人取得 A+成绩，其他人的成绩至少是 B 级及以上，平均分是 64 分，这个班级选考物理学业水
16、平等第 8 页（共 20 页）级考的人数至少为 15 人【分析】可设取得 A 成绩的 x 人，取得 B+成绩的 y 人，取得 B 成绩的 z 人，由题意可得：705+67x+64y+61z64（5+x+y+z） ，解得：zx10，又 x，y，zN，故当且仅当 x0，y0，z10 时，5+x+y+z 取得最小值 15，故得解【解答】解：设取得 A 成绩的 x 人，取得 B+成绩的 y 人，取得 B 成绩的 z 人，则 705+67x+64y+61z64（5+x+y+z） ，即 zx 10，又 x，y，z N，即当且仅当 x0，y 0，z10 时，5+x+y+z 取得最小值 15，取得 A 成绩的
17、 0 人，取得 B+成绩的 0 人，取得 B 成绩的 10 人，这个班级选考物理学业水平等级考的人数至少为 15 人，故答案为：15【点评】本题考查了实际问题通过数学问题解决，考查了阅读理解及数学建模的能力，属中档题9 （5 分）已知函数 f（x ）是以 2 为周期的偶函数，当 0x1 时，f（x）lg（x+1） ，令函数 g（x ） f（x ） （x 1，2） ，则 g（x）的反函数为 g1 （x）310 x（0 xlg2） 【分析】先根据偶函数性质求出 x1，0上的解析式，再根据周期为 2 求出 x1，2上的解析式，最后求出反函数【解答】解：当1x0 时，0x1，f （x）f
18、 （x）lg（x+1） ，当 1x2 时，1x 20，f （x）f （x2）lg（x2）+1lg（x+3） g（x）lg（ x+3） （1x2） ，x+310 g（x） ，x310 g（x） ，故答案为：g 1 （x）310 x， （0xlg2）【点评】本题考查了反函数，属基础题10 （5 分）已知函数 ysinx 的定义域是 a，b，值域是 1， ，则 ba 的最大值是 【分析】根据函数 ysinx，令 a ，要使 ba 的最大值，结合三角函数第 9 页（共 20 页）的图象可得 b ，可得答案；【解答】解：函数 ysinx，令 a ，要使 ba 的最大值，可知 b 的最大值为：b ，ba
19、的最大值为 ；故答案为：【点评】本题考查了正弦函数的图象及性质的应用，属于基础题11 （5 分）已知 R，函数 f（x） ，若函数 f（x）恰有 2 个零点，则 的取值范围是 （1，3（4，+） 【分析】根据题意，在同一个坐标系中作出函数 yx4 和 yx 24x +3 的图象，结合图象分析可得答案【解答】解：根据题意，在同一个坐标系中作出函数 yx4 和 yx 24x +3 的图象，如图：若函数 f（x）恰有 2 个零点，即函数 f（x）图象与 x 轴有且仅有 2 个交点，则 13 或 4，即 的取值范围是：（1，3（4，+）故答案为：（1，3（4，+） 【点评】本题考查分段函数的图象和函数
20、的零点，考查数形结合思想的运用，考查发现问题解决问题的能力第 10 页（共 20 页）12 （5 分）已知圆 M：x 2+（ y1） 21，圆 N：x 2+（y +1） 21直线 l1、l 2 分别过圆心M、N ，且 11 与圆 M 相交于 A，B 两点，1 2 与圆 N 相交于 C，D 两点，点 P 是椭圆1 上任意一点，则 + 的最小值为 8 【分析】由题意可知， ， 1，结合 P 为椭圆上的点，可用 P 的坐标表示，然后结合椭圆的性质即可求解【解答】解：由题意可得，M（0，1） ，N（0，1） ，r Mr N1，（ ）（ ） ，（ ） 1，P 为椭圆 上的点， + 22（x 2+y2）由
21、题意可知，3x3，8 ，故答案为：8【点评】本题主要考查了平面向量数量积的运算及基本不等式的应用，属于知识的简单综合应用二、选择题（本大题共有 4 题，满分 20 分，每题 5 分）每题有且只有一个正确选项.考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.13 （5 分）设 R，则“ ”是“sin ”的（ ）A充分非必要条件 B必要非充分条件C充要条件 D既非充分也非必要条件【分析】由 ，通过运算有 sin ，即“ ”是“sin ”的充分条件，由 sin ，通过解三角方程有：k +（1） k ，即 “ ”是“sin ”的不必要条件，故可得解第 11 页（共 20 页）【解答】
22、解：由 ，则有 sin ，即“ ”是“sin ”的充分条件，由 sin ，得： k+（ 1） k ，即“ ”是 “sin ”的不必要条件，即“ ”是 “sin ”的充分不必要条件故选：A【点评】本题考查了充分条件、必要条件、充要条件，考查了解三角方程，属简单题14 （5 分）魏晋时期数学家刘徽在他的著作九章算术注中，称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖” ，刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为 ：4若正方体的棱长为 2，则“牟合方盖”的体积为（ ）A16 B16 C D【分析】由已知求出正方体内切球的体积，再由已知体积比求得“牟
23、合方盖”的体积【解答】解：正方体的棱长为 2，则其内切球的半径 r1，正方体的内切球的体积 ，又由已知 ， 故选：C【点评】本题考查球的体积的求法，理解题意是关键，是基础题15 （5 分）对于函数 yf（x） ，如果其图象上的任意一点都在平面区域（x，y ）| （y+x）（yx ）0内，则称函数 f（x）为“蝶型函数” ，已知函数： ysinx；y，下列结论正确的是（ ）A、 均不是“蝶型函数”B、 均是 “蝶型函数”C是“蝶型函数” ；不是 “蝶型函数”D不是 “蝶型函数”：是“蝶型函数”【分析】由 g（x）sinx+ x，h（x）sin xx，求得导数判断单调性，结合“蝶型函数
24、”可判断 ；由平方差公式，化简结合“蝶型函数” 可判断【解答】解：由 ysinx，设 g（x）sin x+x，导数为 cosx+10，即有 x0，g（x）第 12 页（共 20 页）0；x0 时，g（x ）0；设 h（x）sinxx，其导数为 cosx10，x0 时，h（x）0，x0 时，h（x）0，可得（y+x） （yx）0 恒成立，即有 ysinx 为“蝶型函数” ；由（ +x） （ x）x 21x 210，可得 y 为“蝶型函数”故选：B【点评】本题考查新定义的理解和运用，考查不等式恒成立问题解法，以及运算能力，属于中档题16 （5 分）已知数列a n是公差不为 0 的等差数列，前 n
25、项和为 Sn，若对任意的 nN*，都有 SnS 3，则 的值不可能为（ ）A2 B C D【分析】由等差数数列前 n 项和公式推导出3da 12d，由此能求出 的值不可能为 【解答】解：数列a n是公差不为 0 的等差数列，前 n 项和为 Sn，对任意的 nN*，都有 SnS 3， ， ，且3da 12d，当 2 时，a 13d成立；当 时，a 1 d成立；当 时，a 12d成立；第 13 页（共 20 页）当 时，a 1d不成立 的值不可能为 故选：D【点评】本题考查等差数列的两项比值的求法，考查等差数列性质等基础知识，考查运算求解能力，考查化归与转化思想，是基础题三、解答题.1
26、7 （14 分）如图，已知正方体 ABCDABC D的棱长为 1（1）正方体 ABCDAB C D'中哪些棱所在的直线与直线 AB 是异面直线？（2）若 M，N 分别是 A'B，BC的中点，求异面直线 MN 与 BC 所成角的大小【分析】 （1）利用列举法能求出直线 AB 是异面直线的棱所在直线（2）M，N 分别是 A'B，BC的中点，以 D 为原点，DA 为 x 轴，DC 为 y 轴，DD为z 轴，建立空间直角坐标系，利用向量法能求出异面直线 MN 与 BC 所成角的大小【解答】解：（1）正方体 ABCDABC D中，直线 AB 是异面直线的棱所在直线有：AD，BC
27、，CD，CD，DD，CC，共 6 条（2）M，N 分别是 A'B，BC的中点，以 D 为原点，DA 为 x 轴，DC 为 y 轴，DD为 z 轴，建立空间直角坐标系，则 A（1，0，1） ，B（1，1，0） ，C （0，1，1） ，M（1， ， ） ，N（ ） ，B（1，1，0） ，C（0，1，0） ，（ ，0） ， （1，0，0） ，设异面直线 MN 与 BC 所成角的大小为 ，第 14 页（共 20 页）则 cos ，45，异面直线 MN 与 BC 所成角的大小为 45【点评】本题考查异面直线的判断，考果异面直线所成角的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推
28、理能力与计算能力，是中档题18 （14 分）已知函数 f（x ） ，其中 aR（1）解关于 x 的不等式 f（x）1；（2）求 a 的取值范围，使 f（ x）在区间（0，+）上是单调减函数【分析】 （1）由题意可得 0，对 a 讨论，可得所求解集；（2）求得 f（x ） a+ ，由反比例函数的单调性，可得22a0，解不等式即可得到所求范围【解答】解：（1）x 的不等式 f（x）1，即为 1，即为 0，当 a1 时，解集为x| x2；当 a1 时，解集为（2，0；当 a1 时，解集为（，2）0，+ ） ；（2）f（x） a+ ，由 f（x）在区间（ 0，+）上是单调减函数，可得22a0，解得 a
29、1第 15 页（共 20 页）即 a 的范围是（，1） 【点评】本题考查分式不等式的解法，注意运用分类讨论思想方法，考查函数的单调性的判断和运用，考查运算能力，属于基础题19 （14 分）我国的“洋垃极禁止入境”政策已实施一年多某沿海地区的海岸线为一段圆弧 AB，对应的圆心角 AOB ，该地区为打击洋垃圾走私，在海岸线外侧 20 海里内的海域 ABCD 对不明船只进行识别查证（如图：其中海域与陆地近似看作在同一平面内）在圆弧的两端点 A，B 分别建有监测站，A 与 B 之间的直线距离为 100 海里（1）求海域 ABCD 的面积；（2）现海上 P 点处有一艘不明船只，在 A 点测得其距 A 点
30、 40 海里，在 B 点测得其距B 点 20 海里判断这艘不明船只是否进入了海域 ABCD？请说明理由【分析】 （1）利用扇环的面积公式求出海域 ABCD 的面积；（2）由题意建立平面直角坐标系，利用坐标求出点 P 的位置，判断点 P 是否在海域ABCD 内【解答】解：（1）AOB ，在海岸线外侧 20 海里内的海域 ABCD，AB100ADBC20，OAOB AB100，ODOA +AD100+20120，S ABCD （OD 2OA 2） （120 2100 2） （平方海里） ，（2）由题意建立平面直角坐标系，如图所示；由题意知，点 P 在圆 B 上，即（x100） 2+y27600，第
31、 16 页（共 20 页）点 P 也在圆 A 上，即（x 50） 2+ 1600；由组成方程组，解得 或 ；又区域 ABCD 内的点满足 ，由 302+ 360010000，点（30，30 ）不在区域 ABCD 内，由 902+ 1560014400，点（90，50 ）也不在区域 ABCD 内；即这艘不明船只没进入了海域 ABCD【点评】本题考查了圆的方程模型应用问题，是中档题20 （16 分）已知椭圆 ： 1（ab0）的长轴长为 2 ，右顶点到左焦点的距离为 +1，直线 l：ykx+m 与椭圆 交于 A，B 两点（1）求椭圆 的方程；（2）若 A 为椭圆的上项点，M 为 AB 中点，O 为坐
32、标原点，连接 OM 并延长交椭圆 于 N， ，求 k 的值（3）若原点 O 到直线 l 的距离为 1， ，当 时，求OAB 的面积S 的范围第 17 页（共 20 页）【分析】 （1）先根据已知条件可求出 a、c 的值，结合 a、b、c 的值可得出 b 的值，进而可求出椭圆 的标准方程；（2）先得出直线 l 的方程为 ykx+1 ，将直线 l 的方程代入椭圆方程可求出点 B 的坐标，利用中点坐标公式可得出点 M 的坐标，根据已知条件可得出点 N 的坐标，再将点 N 的坐标代入椭圆的方程，即可求出 k 的值；（3）利用原点 O 到直线 l 的距离可得出 m2k 2+1，将直线 l 的方程与椭圆方
33、程联立，列出韦达定理，将韦达定理代入 ，结合 的取值范围可得出 k2 的取值范围，并求出线段 AB 的长度的表达式，可求出| AB|的取值范围，再利用三角形的面积公式可求出 S 的取值范围【解答】解：（1）由题意可知， ，于是得到 ，因为右顶点到左焦点的距离为 ，所以，c1，则 ，因此，椭圆 的方程为 ；（2）当点 A 为椭圆的上顶点时，点 A 的坐标为（1，0） ，则 m1，直线 l 的方程为ykx +1，将直线 l 的方程代入椭圆的方程并化简得（ 2k2+1）x 2+4kx0，解得 ，所以点 B 的坐标为 ，由于点 M 为线段 AB 的中点，则点 M 的坐标为 ，由于 ，所以，点 N 的坐
34、标为 ，第 18 页（共 20 页）将点 N 的坐标代入椭圆的方程得 ，化简得，解得 ；（3）由于点 O 到直线 l 的距离为 1，则有 ，所以，m 2k 2+1设点 A（x 1，y 1） 、B（x 2，y 2） ，将直线 l 的方程代入椭圆方程并化简得（2k 2+1）x2+4kmx+2m220，由韦达定理可得 ， ，x 1x2+（kx 1+m） （kx 2+m） ，由于 ，即 ，解得 ，线段 AB 的长为 ，所以， 因此，OAB 的面积 S 的取值范围是 【点评】本题考查直线与椭圆的综合问题，考查韦达定理在椭圆中的应用，考查计算能力与推理能力，属于难题21 （18 分）已知项数为 n0（n
35、04）项的有穷数列a n，若同时满足以下三个条件：a1 1，a m（m 为正整数） ； aia i1 0 或 1，其中 i2，3，n 0；第 19 页（共 20 页）任取数列 an中的两项 ap，a q（pq） ，剩下的 n02 项中一定存在两项as， at（s t） ，满足 ap+aqa s+at，则称数列 an为 数列（1）若数列a n是首项为 1，公差为 1，项数为 6 项的等差数列，判断数列 an是否是数列，并说明理由（2）当 m3 时，设 数列 an中 1 出现 d1 次，2 出现 d2 次，3 出现 d3 次，其中d1，d 2，d 3N*求证：d 14，d 22，d 34；（3）当
36、 m2019 时，求 数列 an中项数 n0 的最小值【分析】 （1）根据 数列的定义判断即可；（2）根据 数列的定义证明即可；（3）先证明项数 n0 的最小值是 2027：再证明上述数列是 数列，从而判断即可【解答】解：（1）若数列a n：1，2，3，4，5，6 是 数列，取数列a n中的两项 1 和 2，则剩下的 4 项中不存在两项 as，a t（st） ，使得 1+2a s+at，故数列a n不是 数列；（2）若 d13，对于 p1，q2，若存在 2st，满足 ap+aqa s+at，2st，于是 s3，t4，故 a5a 2，a ta 1，从而 as+ata 2+a1，矛盾，故 d14，
37、同理 d34，下面证明 d22：若 d21，即 2 出现了 1 次，不妨设 ak2，a 1+aka s+at，等式左边是 3，等式右边有几种可能，分别是 1+1 或 1+3 或 3+3，等式两边不相等，矛盾，于是 d12；（3）设出现 d1 次，2 出现 d2 次，2019 出现 d2019 次，其中 d1，d 2，d 2019N*，由（2）可知，d 14，d 20194，且 d22，同理 d20182，又d 3，d 4，d 2017N*，故项数 n0d 1+d2+d2019 2027，下面证明项数 n0 的最小值是 2027：第 20 页（共 20 页）取 d14，d 22，d 3d 4d
38、20171，d 20182，d 20194，可以得到数列a n：1，1，1，1，2，2，3，4，2016，2017，2018，2019，2019，2019，2019，接下来证明上述数列是 数列：若任取的两项分别是 1，1，则其余的项中还存在 2 个 1，满足 1+11+1，同理，若任取的两项分别是 2019，2019 也满足要求，若任取的两项分别是 1，2，则其余的项中还存在 3 个 1，1 个 2，满足要求，同理，若任取的两项分别是 2018，2019 也满足要求，若任取 ap1，a q3，则在其中的项中取 a52，a ta q 1，满足要求，同理，若 ap2017，a q2019 也满足要求，若任取的两项 ap，a q 满足 1a pa q2019，则在其余的项中选取 asa p1，a ta q+1，每个数最多被选取了 1 次，于是也满足要求，从而，项数 n0 的最小值是 2027【点评】本题考查了新定义问题，考查数列的证明以及转化思想，是一道综合题
