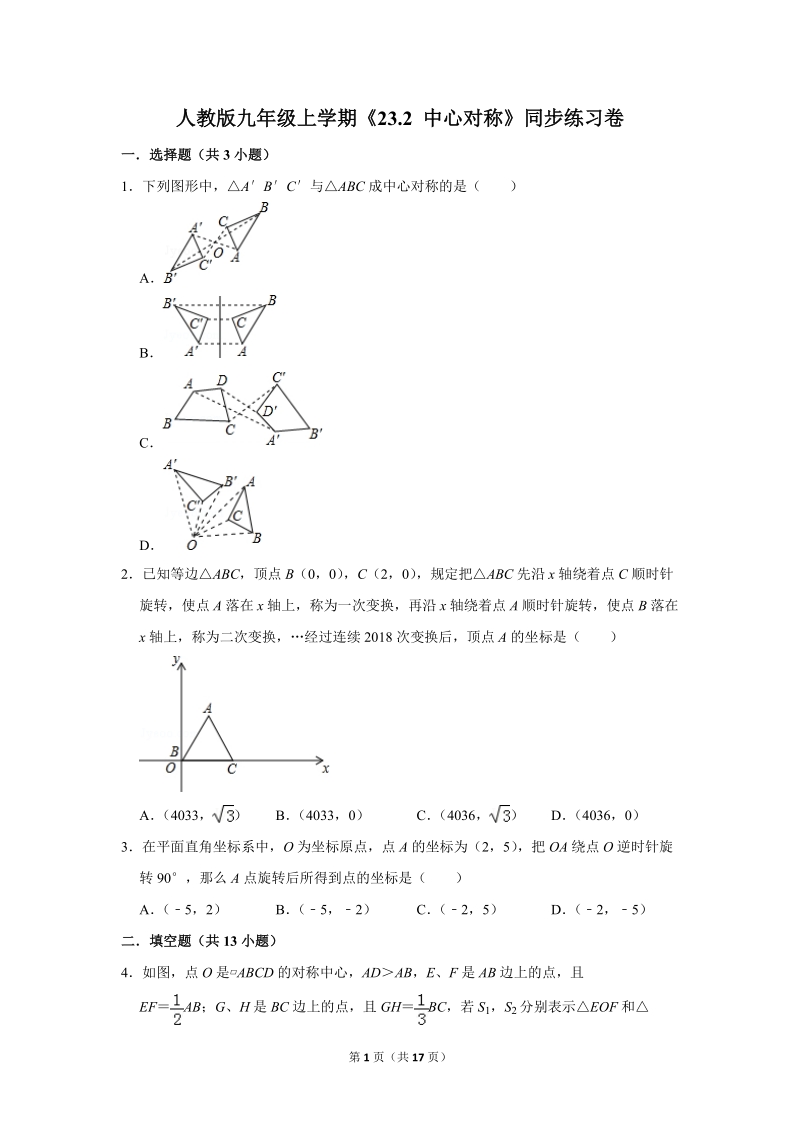
1、第 1 页（共 17 页）人教版九年级上学期23.2 中心对称同步练习卷一选择题（共 3 小题）1下列图形中，ABC 与ABC 成中心对称的是（ ）ABCD2已知等边ABC，顶点 B（0，0） ，C（2，0） ，规定把ABC 先沿 x 轴绕着点 C 顺时针旋转，使点 A 落在 x 轴上，称为一次变换，再沿 x 轴绕着点 A 顺时针旋转，使点 B 落在x 轴上，称为二次变换， 经过连续 2018 次变换后，顶点 A 的坐标是（ ）A （4033， ） B （4033，0） C （4036， ） D （4036，0）3在平面直角坐标系中，O 为坐标原点，点 A 的坐标为（2，5） ，把 OA 绕点
2、 O 逆时针旋转 90，那么 A 点旋转后所得到点的坐标是（ ）A （5，2） B （5，2） C （2，5） D （2，5）二填空题（共 13 小题）4如图，点 O 是ABCD 的对称中心， ADAB，E 、F 是 AB 边上的点，且EF AB；G、H 是 BC 边上的点，且 GH BC，若 S1，S 2 分别表示EOF 和第 2 页（共 17 页）GOH 的面积，则 S1 与 S2 之间的等量关系是 5如图，在ABC 中，点 O 是 AC 的中点，CDA 与ABC 关于点 O 中心对称，若AB 6，BAC40，则 CD 的长度为 ，ACD 的度数为 6如图，在O 中，AB 为O 的直径，A
3、B4动点 P 从 A 点出发，以每秒 个单位的速度在 O 上按顺时针方向运动一周设动点 P 的运动时间为 t 秒，点 C 是圆周上一点，且AOC40，当 t 秒时，点 P 与点 C 中心对称，且对称中心在直径 AB上7如图，正方形 ABCD 内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，设黑色部分的面积为 S，正方形的边长为 2，则 S 8小明把如图所示的平行四边形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等） ，则飞镖落在阴影区域的概率是 9以下几何图形中：等边三角形； 矩形；平行四边形； 等腰三角形；菱第
4、3 页（共 17 页）形既是轴对称图形，又是中心对称图形的是 （填序号） 10下列图形中，等腰三角形； 平行四边形；等腰梯形； 圆；正六边形；菱形； 正五边形，是中心对称图形的有 （填序号）11已知点 P（a+1，1）关于原点的对称点在第四象限，则 a 的取值范围是 12已知点 P（2m1，m+3）关于原点的对称点在第三象限，则 m 的取值范围是 13在直角坐标系中，点 A（1，2）关于原点对称的点的坐标是 14点 A（m，n2）与点 B（2，n）关于原点对称，则点 A 的坐标为 15如图，在平面直角坐标系中，已知点 A（3，0） ，B（0，4） ，如果将线段 AB 绕点 B 顺时针旋转 90
5、至 CB，那么点 C 的坐标是 16点 A 的坐标为（0， ） ，把点 A 绕着坐标原点逆时针旋转 135到点 P，那么点 P 的坐标是 三解答题（共 4 小题）17如图，矩形 ABCD 和矩形 AEFG 关于点 A 中心对称，（1）四边形 BDEG 是菱形吗？请说明理由（2）若矩形 ABCD 面积为 6，求四边形 BDEG 的面积18如图，由 4 个全等的正方形组成的 L 形图案，请按下列要求画图：（1）在图案中添加 1 个正方形，使它成轴对称图形（不能是中心对称图形） ；（2）在图案中添加 1 个正方形，使它成中心对称图形（不能是轴对称图形） ；（3）在图案中改变 1 个正方形的位置，从而
6、得到一个新图形，使它既成中心对称图形，又成轴对称图形第 4 页（共 17 页）19若点 A（a2，3）和点 B（1，2b+2）关于原点对称，求 a，b 的值20如图所示，在平面直角坐标系中，已知点 A（4，0） 、B（0，3） ，对AOB 连续作旋转变换可以依次得到三角形（1） 、 （2） 、 （3） 、 （4） 、请你仔细观察图形，并解决以下问题：（1）第（2）个三角形的直角顶点坐标是 ；（2）第（5）个三角形的直角顶点坐标是 ；（3）第（2018）个三角形的直角顶点坐标是 第 5 页（共 17 页）参考答案与试题解析一选择题（共 3 小题）1下列图形中，ABC 与ABC 成中心对称的是（
7、）ABCD【分析】根据中心对称，轴对称，平移变换的性质对各选项分析判断即可得解【解答】解：A、是中心对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是旋转变换图形，故本选项错误；D、是旋转变换图形，故本选项错误故选：A【点评】本题考查中心对称的性质，关键是根据中心对称，轴对称，平移变换的性质解答2已知等边ABC，顶点 B（0，0） ，C（2，0） ，规定把ABC 先沿 x 轴绕着点 C 顺时针旋转，使点 A 落在 x 轴上，称为一次变换，再沿 x 轴绕着点 A 顺时针旋转，使点 B 落在x 轴上，称为二次变换， 经过连续 2018 次变换后，顶点 A 的坐标是（ ）第 6 页（共
8、17 页）A （4033， ） B （4033，0） C （4036， ） D （4036，0）【分析】利用已知点坐标得出等边ABC 边长为 2，根据三角函数可得等边ABC 的高，顶点 A 的坐标分别为（4，0） ， （4，0） ， （7， ） ， （10，0） ， （10，0） ， （13， ） ，进而得出点的坐标变化规律，即可得出答案【解答】解：顶点 A 的坐标分别为（4，0） ， （4，0） ， （7， ） ， （10，0） ， （10，0） ，（13， ） ，201836722，6726+44036，故顶点 A 的坐标是（4036，0） 故选：D【点评】此题主要考查了坐标与图形的变化，
9、正确得出点的坐标变化规律是解题关键3在平面直角坐标系中，O 为坐标原点，点 A 的坐标为（2，5） ，把 OA 绕点 O 逆时针旋转 90，那么 A 点旋转后所得到点的坐标是（ ）A （5，2） B （5，2） C （2，5） D （2，5）【分析】首先根据旋转的性质作图，利用图象则可求得点 B 的坐标【解答】解：过点 B 作 BCx 轴于点 C，过点 B 作 BCy 轴于点 F，点 A 的坐标为（2，5） ，将 OA 绕原点 O 逆时针旋转 90到 OB 的位置，第 7 页（共 17 页）BC2，CO5点 B 的坐标为：（5，2） ，故选：A【点评】此题考查了旋转的性质，解题的关键是数形结合
10、思想的应用得出 BC，BF 的长二填空题（共 13 小题）4如图，点 O 是ABCD 的对称中心， ADAB，E 、F 是 AB 边上的点，且EF AB；G、H 是 BC 边上的点，且 GH BC，若 S1，S 2 分别表示EOF 和GOH 的面积，则 S1 与 S2 之间的等量关系是 【分析】根据同高的两个三角形面积之比等于底边之比得出 ， ，再由点 O 是ABCD 的对称中心，根据平行四边形的性质可得 SAOB S BOC SABCD，从而得出 S1 与 S2 之间的等量关系【解答】解： ， ，S 1 SAOB ，S 2 SBOC 点 O 是ABCD 的对称中心，S AOB S BOC S
11、ABCD， 即 S1 与 S2 之间的等量关系是 第 8 页（共 17 页）故答案为 【点评】本题考查了中心对称，三角形的面积，平行四边形的性质，根据同高的两个三角形面积之比等于底边之比得出 ， 是解题的关键5如图，在ABC 中，点 O 是 AC 的中点，CDA 与ABC 关于点 O 中心对称，若AB 6，BAC40，则 CD 的长度为 6 ，ACD 的度数为 40 【分析】直接利用中心对称图形的性质得出四边形 ABCD 是平行四边形，进而得出答案【解答】解：点 O 是 AC 的中点，CDA 与ABC 关于点 O 中心对称，四边形 ABCD 是平行四边形，ABDC6，AB DC ，BACACD
12、40故答案为：6，40【点评】此题主要考查了中心对称图形的性质，正确得出四边形 ABCD 是平行四边形是解题关键6如图，在O 中，AB 为O 的直径，AB4动点 P 从 A 点出发，以每秒 个单位的速度在 O 上按顺时针方向运动一周设动点 P 的运动时间为 t 秒，点 C 是圆周上一点，且AOC40，当 t 或 或 或 秒时，点 P 与点 C 中心对称，且对称中心在直径 AB 上【分析】根据中心对称的定义，可得 P 点的位置，根据弧长公式，可得 ，根据路程除以速度等于时间，可得答案第 9 页（共 17 页）【解答】解：如图 ，当AOP 140时，P 1 与 C1 对称， 4 ，t ；当AOP
13、2140时，P 2 与 C1 对称， 4 ，t ；当AOP 3220时，P 3 与 C2 对称， 4 ，t ；当AOP 4320时，P 4 与 C1 对称， 4 ，t ；故答案为： 或 或 或 【点评】本题考查了中心对称，利用中心对称得出 P 点的位置是解题关键，又利用了弧长公式，要分类讨论，以防遗漏7如图，正方形 ABCD 内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，设黑色部分的面积为 S，正方形的边长为 2，则 S 【分析】根据中心对称图形的性质可得黑色部分的面积等于白色部分的面积为 S，进而可得圆的面积，然后再表示出圆的半径，根据图形可得
14、2r2，进而可得 r，再求 S 即可【解答】解：正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称，黑色部分的面积等于白色部分的面积为 S，S 圆 2S，设半径为 r，则 r22S，r ，正方形的边长为 2，第 10 页（共 17 页）2r2，r1， 1，S ，故答案为： 【点评】此题主要考查了中心对称图形，关键是掌握中心对称图形的性质，掌握圆的面积公式8小明把如图所示的平行四边形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等） ，则飞镖落在阴影区域的概率是 【分析】先根据平行四边形的性质求出平行四边形对角线所分的四个三角形面积相等，再求出 S1S
15、 2 即可【解答】解：根据平行四边形的性质可得：平行四边形的对角线把平行四边形分成的四个面积相等的三角形，根据平行线的性质可得 S1S 2，则阴影部分的面积占 ，则飞镖落在阴影区域的概率是 故答案为： 【点评】此题主要考查了几何概率，以及中心对称图形，用到的知识点为：概率相应的面积与总面积之比，关键是根据平行线的性质求出阴影部分的面积与总面积的比9以下几何图形中：等边三角形； 矩形；平行四边形； 等腰三角形；菱形既是轴对称图形，又是中心对称图形的是 （填序号） 【分析】根据轴对称图形与中心对称图形的概念求解如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称
16、轴如果一个图形第 11 页（共 17 页）绕某一点旋转 180后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心【解答】解：等边三角形是轴对称图形，不是中心对称图形，不符合题意；矩形是轴对称图形，也是中心对称图形，符合题意；平行四边形不是轴对称图形，是中心对称图形，不符合题意；等腰三角形是轴对称图形，不是中心对称图形，不符合题意；菱形是轴对称图形，也是中心对称图形，符合题意故答案为： 【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部分重合10下列图形中，等腰三角形； 平
17、行四边形；等腰梯形； 圆；正六边形；菱形； 正五边形，是中心对称图形的有 （填序号）【分析】结合中心对称图形的概念进行求解即可【解答】解：是中心对称图形的有：平行四边形；圆； 正六边形；菱形故答案为：【点评】本题考查了中心对称图形的概念中心对称图形是要寻找对称中心，旋转 180度后两部分重合11已知点 P（a+1，1）关于原点的对称点在第四象限，则 a 的取值范围是 a1 【分析】首先根据题意判断出 P 点在第二象限，再根据第二象限内点的坐标符号（，+） ，可得到不等式 a+10，然后解出 a 的范围即可【解答】解：P（a+1，1）关于原点对称的点在第四象限，P 点在第二象限，a+10，解得：
18、a1，故答案为：a1【点评】此题主要考查了关于原点对称的点的坐标特点，以及各象限内点的坐标符号，关键是判断出 P 点所在象限12已知点 P（2m1，m+3）关于原点的对称点在第三象限，则 m 的取值范围是 第 12 页（共 17 页）m3 【分析】根据关于原点对称点的性质可得 P 在第一象限，进而可得 ，再解不等式组即可【解答】解：点 P（2m1 ，m +3）关于原点的对称点在第三象限，点 P（2m1，m+3）在第一象限， ，解得： m3，故答案为： m3【点评】此题主要考查了关于原点对称的点的坐标特点，关键是掌握各象限内点的坐标符号13在直角坐标系中，点 A（1，2）关于原点对称的点的坐标是
19、 （1，2） 【分析】根据“平面直角坐标系中任意一点 P（x，y ） ，关于原点的对称点是（x，y） ，即关于原点的对称点，横纵坐标都变成相反数”解答【解答】解：根据关于原点对称的点的坐标的特点，点（1，2）关于原点过对称的点的坐标是（1，2） 故答案为：（1，2） 【点评】本题主要考查了关于原点对称的点的坐标的特点，正确掌握横纵坐标的关系是解题关键14点 A（m，n2）与点 B（2，n）关于原点对称，则点 A 的坐标为 （2，1） 【分析】根据两个点关于原点对称时，它们的坐标符号相反，可得 m、n 的值，进而求得结论【解答】解：由 A（m，n2 ）与点 B（2，n）关于原点对称，得m+（ 2
20、）0 ，n2+ n0解得 m2，n1n2121，A 点坐标为（2，1） 第 13 页（共 17 页）故答案为：（2，1） 【点评】此题主要考查了关于原点对称的点的坐标，关键是掌握点的坐标的变化规律，关于原点对称的横坐标互为相反数，纵坐标互为相反数15如图，在平面直角坐标系中，已知点 A（3，0） ，B（0，4） ，如果将线段 AB 绕点 B 顺时针旋转 90至 CB，那么点 C 的坐标是 （4，1） 【分析】作 CDy 轴于点 D，如图，根据旋转的性质得 ABC90，BCBA，再利用等角的余角相等得到CBDA，则可证明ABOBCD 得到BDOA3，CDOB4，然后根据第二象限内点的坐标特征写出
21、 C 点坐标【解答】解：如图，作 CDy 轴于点 D，A（3，0） ，B（0，4） ，OA3，OB4，线段 AB 绕点 B 顺时针旋转 90至 CB，ABC90，BCBA ，ABO+A90，ABO+CBD90，CBDA，在ABO 和BCD 中，ABOBCD（AAS ） ，BDOA 3，CDOB4，ODOB BD 431，C 点坐标为（4，1） 故答案为：（4，1） 第 14 页（共 17 页）【点评】本题考查了坐标与图形变化旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标解决本题的关键是作 CDy 轴于点 D 后求出CD 和 OD 的长16点 A 的坐标为（0， ）
22、 ，把点 A 绕着坐标原点逆时针旋转 135到点 P，那么点 P 的坐标是 （1，1） 【分析】如图作 PEx 轴于 E解直角三角形POE 即可【解答】解：如图作 PEx 轴于 E由题意：OPOA ，POE45，OEPE1，P（1，1） ，故答案为（1，1） 【点评】本题考查坐标与图形变化旋转，解题的关键是理解题意，学会添加常用辅助线面构造直角三角形解决问题三解答题（共 4 小题）17如图，矩形 ABCD 和矩形 AEFG 关于点 A 中心对称，（1）四边形 BDEG 是菱形吗？请说明理由（2）若矩形 ABCD 面积为 6，求四边形 BDEG 的面积【分析】 （1）对角线互相垂直的平行四边形是
23、菱形，直接利用菱形的判定方法得出答案；（2）直接利用矩形的面积结合菱形的面积计算公式得出答案【解答】解：（1）四边形 BDEG 是菱形理由：矩形 ABCD 和矩形 AEFG 关于点 A 中心对称，第 15 页（共 17 页）ABAE，ADAG，四边形 BDEG 是平行四边形，又BAD90，BAEDAG180，BEDG，四边形 BDEG 是菱形（2）矩形 ABCD 面积为 6，ADAB6，S 菱形 BDEG BEDG 2AB2AD12【点评】此题主要考查了中心对称以及菱形的判定，正确把握菱形的判定是解题关键18如图，由 4 个全等的正方形组成的 L 形图案，请按下列要求画图：（1）在图案中添加
24、1 个正方形，使它成轴对称图形（不能是中心对称图形） ；（2）在图案中添加 1 个正方形，使它成中心对称图形（不能是轴对称图形） ；（3）在图案中改变 1 个正方形的位置，从而得到一个新图形，使它既成中心对称图形，又成轴对称图形【分析】 （1）根据轴对称图形的性质，先找出对称轴，再思考如何画图；（2）如一，也是先找一个中心，再根据中心对称的性质，思考如何画图；（3）根据中心对称和轴对称的性质画一个图形注意此题有多种画法，答案不唯一【解答】解：如图所示（1）如图（1） ，图（2） ，图（3）所示；（2）如图（4）所示；第 16 页（共 17 页）（3）如图（5） ，图（6）所示【点评】本题综合考
25、查了中心对称图形及轴对称图形的性质，及其作图的方法，学生做这些题时找对称轴及对称点是关键19若点 A（a2，3）和点 B（1，2b+2）关于原点对称，求 a，b 的值【分析】根据关于原点对称的点的坐标特点进行解答即可【解答】解：点 A（a2，3）和点 B（1，2b+2）关于原点对称，a2（1） ，3（2b+2） ，解得 a3，b 【点评】本题考查的是关于原点对称的点的坐标特点，即关于原点对称的点的坐标，横、纵坐标均互为相反数20如图所示，在平面直角坐标系中，已知点 A（4，0） 、B（0，3） ，对AOB 连续作旋转变换可以依次得到三角形（1） 、 （2） 、 （3） 、 （4） 、请你仔细观
26、察图形，并解决以下问题：（1）第（2）个三角形的直角顶点坐标是 （4 ， ） ；（2）第（5）个三角形的直角顶点坐标是 （16 ， ） ；（3）第（2018）个三角形的直角顶点坐标是 （8068 ， ） 【分析】利用勾股定理列式求出 AB 的长，再根据图形写出第（3）个三角形的直角顶点第 17 页（共 17 页）的坐标即可；观察图形不难发现，每 3 个三角形为一个循环组依次循环，用 2018 除以3，根据商和余数的情况确定出第（2018）个三角形的直角顶点的坐标即可【解答】解：点 A（4，0） ，B（0，3） ，OA4，OB3，AB 5，第（2）个三角形的直角顶点的坐标是（4 ， ） ；第（5）个三角形的直角顶点的坐标是（16 ， ）20183672 余 2，第（2018）个三角形是第 673 组的第二个直角三角形，672128064，第（2018）个三角形的直角顶点的坐标是（8068 ， ） 故答案为：（4 ， ） ；（16 ， ） ；（8068 ， ） 【点评】本题考查了坐标与图形变化旋转，勾股定理的应用，观察图形，发现每 3 个三角形为一个循环组依次循环是解题的关键
