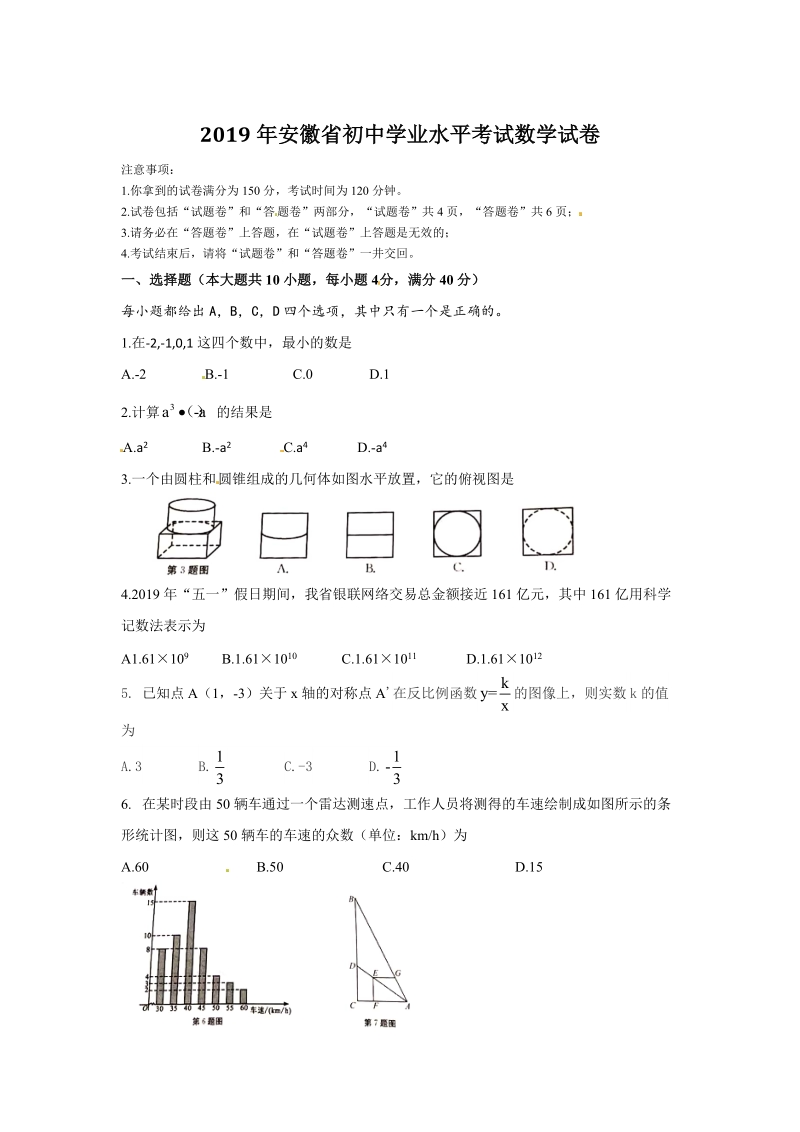
1、2019 年安徽省初中学业水平考试数学试卷注意事项：1.你拿到的试卷满分为 150 分，考试时间为 120 分钟。来源:学+科+ 网2.试卷包括“试题卷”和“答 题卷”两部分，“试题卷”共 4 页，“答题卷”共 6 页；3.请务必在“答题卷”上答题，在“试题卷”上答题是无效的；4.考试结束后，请将“试题卷”和“答题卷”一井交回。一、选择题（本大题共 10 小题，每小题 4分，满分 40 分）每小题都给出 A，B，C，D 四个选项，其中只有一个是正确的。1.在-2,-1,0,1 这四个数中，最小的数是A.-2 B.-1 C.0 D.12.计算 的结果是3a-（ ）A.a2 B.-a2 C.a4
2、D.-a4 来源:学科网3.一个由圆柱和 圆锥组成的几何体如图水平放置，它的俯视图是4.2019 年“五一”假日期间，我省银联网络交易总金额接近 161 亿元，其中 161 亿用科学记数法表示为A1.61109 B.1.611010 C.1.611011 D.1.6110125. 已知点 A（1，-3）关于 x 轴的对称点 A在反比例函数 的图像上，则实数 k 的值ky=x为A.3 B. C.-3 D.31-36. 在某时段由 50 辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这 50 辆车的车速的众数（单位：km/h）为 A.60 B.50 C.40 D.15来
3、源:学|科|网7. 如图，在科 RtABC 中，ACB=90，AC=6，BC=12，点 D 在边 BC 上，点 E 在线段AD 上，EFAC 于点 F，EGEF 交 AB 于点 G，若 EF=EG，则 CD 的长为A. 3.6 B.4 C.4.8 D.58. 据国家统计局数据，2018 年全年国内生产总值为 90.3 万亿，比 2017 年增长 6.6%.假设国内生产总值的年增长率保持不变，则国内生产总值首次突破 100 万亿的年份是A.2019 年 B.2020 年 C.2021 年 D.2022 年9. 已知三个实数 a,b,c 满足 a-2b+c=0，a+2b+c0，则A. b0，b 2
4、-ac0 B.b0，b 2-ac0B. b0，b 2-ac0 D.b0，b 2-ac010. 如图，在正方形 ABCD 中，点 E，F 将对角线 AC 三等分，且 AC=12，点 P 在正方形的边上，则满足 PE+PF=9 的点 P 的个数是A.0 B.4 C.6 D.82、 填空题(本大共 4 小题，每小题 5 分，满分 30 分)11. 计算 的结果是 。1812 命题“如果 a+b=0，那么 a，b 互为相反数”的逆命题为_.13.如图，ABC 内接于O ，CAB=30，CBA=45，CD AB于点 D，若O 的半径为 2，则 CD 的长为 。14.在平面直角坐标系中，垂直于 x 轴的直
5、线 l 分别于函数 y=x-a+1和 y+x2-2ax 的图像相交于 P，Q 两点.若平移直线 l，可以使 P，Q都在 x 轴的下方，则实数 a 的取值范围是 。3、 （本大题共 2 小 题，每小题 8 分，满分 16 分）15.解方程 1=4（ ）16.如图，在边长为 1 个单位长度的小正方形组成的 1212 的网格中，给出了以格点（网格线的交点）为端点的线段 AB.（1 ）将线段 AB 向右平移 5 个单位，再向上平移 3 个单位得到线段 CD，请画出线段 CD.（2 ）以线段 CD 为一边，作一个菱形 CDEF，且点 E，F 也为格点 .（作出一个菱形即可）四、(本大题共 2 小题，每小
6、题 8 分，满分 16 分)17.为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路.其中一段长为 146 米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2 天后，乙工程队加入，两工程队又联合工作了 1 天，这 3 天共掘进 26 米.已知甲工程队每天比乙工程队多掘进 2 米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？18. 观察以下等式:第 1 个等式: ，21=第 2个等式: ，36第 3 个等式: ，51第 4 个等式: ，=728第 5 个等式: ，94按照以上规律，解决下列问题：（1 ）写出第 6 个等式： ；（2 ）
7、写出你猜想的第 n 个等式： (用含 n 的等式表示)，并证明 .五、(本大题共 2 小题，每小题 10 分，满分 20 分)19.筒车是我国古代发明的一种水利灌溉工具.如图 1，明朝科学家徐光启在农政全书中用图画描绘了筒车的工作原理.如图 2，筒车盛水桶的运行轨迹是以轴心 O 为圆心的圆.已知圆心在水面上方，且圆被水面截得的弦 AB 长为 6 米，OAB=41.3，若点 C 为运行轨道的最高点（C，O 的连线垂直于 AB），求点 C 到弦 AB 所在直线的距离.（参考数据：sin41.30.66，cos41.30.75，tan41.30.88）20.如图，点 E 在ABCD 内部， AFBE
8、，DFCE.（1 ）求证：BCEADF；（2 ）设ABCD 的面积为 S，四边形 AEDF 的面积为 T，求 的值S六、(本题满分 12 分)21.为监控某条生产线上产品的质量，检测员每个相同时间抽取一件产品，并测量其尺寸，在一天的抽检结束后，检测员将测得的个数据按从小到大的顺序整理成如下表格：编号 尺寸（cm） 8.72 8.88 8.92 8.93 8.94 8.96 8.97 8.98a 9.03 9.04 9.06 9.07 9.08b按照生产标准，产品等次规定如下：尺寸（单位：cm） 产品等次8.97x9.03 特等品8.95x9.05 优等品8.90x9.10 合格品x8.90 或
9、 x9.10 非合格品注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）仅算在内.（1 ） 已知此次抽检的合格率为 80%，请判断编号为 的产品是否为合格品，并说明理由（2 ） 已知此次抽检出的优等品尺寸的中位数为 9cm.（i）求 a 的值（ii）将这些优等品分成两组，一组尺寸大于 9cm，另一组尺寸不大于 9cm，从这两组中各随机抽取 1 件进行复检，求抽到的 2 件产品都是特等品的概率 .七、（本题满分 12 分）22.一次函数 y=kx+4 与二次函数 y=ax2+c 的图像的一个交点坐标为（ 1,2），另一个交点是该二次函数图像的顶点（1）求 k，a，
10、c 的值；（2）过点 A（0，m）（0m 4）且垂直于 y 轴的直线与二次函数 y=ax2+c 的图像相交于B，C 两点，点 O 为坐标原点，记 W=OA2+BC2，求 W 关于 m 的函数解析式，并求 W 的最小值.八、（本题满分 14 分）23.如图，RtABC 中， ACB=90，AC=BC，P 为ABC 内部一点，且APB=BPC=135 （1）求证：PABPBC（2）求证：PA=2PC（3）若点 P 到三角形的边 AB，BC，CA 的距离分别为 h1，h 2，h 3，求证 h12=h2h3参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10答案 A D C B A C B
11、 B D D二、填空题11.3 12.如果 a，b 互为相反数，那么 a+b=0 13. 14.a1 或 a-12三、15.x=-1 或 x=316.如图（菱形 CDEF 不唯一）四、17. 设甲工程队每天掘进 x 米，则乙工程队每天掘进（x-2 ）米由题意得 2x+（x+x-2）=26，解得 x=7，所以乙工程队每天掘进 5 米，（天）146-2=075答：甲乙两个工程队还需联合工作 10 天18.（ 1） 6（2 ） 1=n-2n-（ ）证明：右边 左边.等式成立-1+2=n-（ ） （ ）五、19.解：6.64 米20.解：（1 ）证明略（2 ） =2ST六、21. 解：（1 ）不合格
12、.因为 1580%=12，不合格的有 15-12=3 个，给出的数据只有两个不合格；（2 ）优等品有 ，中位数在8.98，a 之间， ，解得 a=9.028.9a=2（3）大于 9cm 的有 ，小于 9cm 的有，期中特等品为画树状图为：共有九种等可能的情况，其中抽到两种产品都是特等品的情况有 4 中抽到两种产品都是特等品的概率 P= 49七、22. 解：（1）由题意得，k+4=-2，解得 k=-2，又二次函数顶点为（0,4），c=4把（1,2）带入二次函数表达式得 a+c=2，解得 a=-2（2）由（1）得二次函数解析式为 y=-2x2+4，令 y=m，得 2x2+m-4=0 ，设 B，C
13、两点的坐标分别为（x 1，m）（x 2，m），则 ，4-mx= 124-mx=W=OA 2+BC2= 224-+8=-7（ ）当 m=1 时， W 取得最小值 7八、23. 解（1）ACB=90，AB=BC ，ABC=45 = PBA+PBC又APB=135，PAB+PBA=45PBC=PAB又APB=BPC=135 ， PABPBC（2）PABPBC PAB=C在 Rt ABC 中，AB=AC， 2 PA=2PCPB=2CAPB，（）过点 P 作 PDBC，PE AC 交 BC、AC 于点 D，ECPB+ APB=135 +135=270APC=90，EAP+ ACP=90,又ACB=ACP+PCD=90EAP=PCD，RtAEPRtCDP ， ，即 ，PEA=2DC32h=32hPAB PBC， 1122hB=h=， 即 1223
