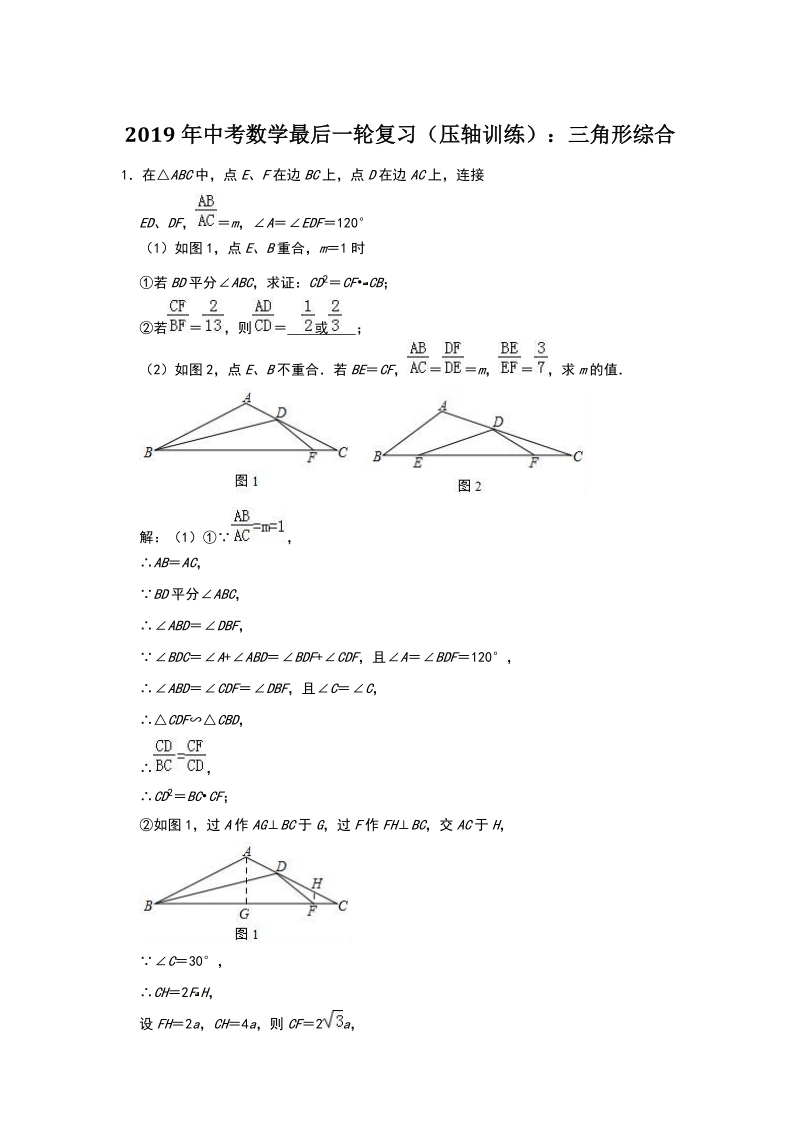
1、2019 年中考数学最后一轮复习（压轴训练）：三角形综合1在 ABC 中，点 E、 F 在边 BC 上，点 D 在边 AC 上，连接ED、 DF， m， A EDF120（1）如图 1，点 E、 B 重合， m1 时若 BD 平分 ABC，求证： CD2 CF CB；若 ，则 或 ；（2）如图 2，点 E、 B 不重合若 BE CF， m， ，求 m 的值解：（1） ， AB AC， BD 平分 ABC， ABD DBF， BDC A+ ABD BDF+ CDF，且 A BDF120， ABD CDF DBF，且 C C， CDF CBD， ， CD2 BCCF；如图 1，过 A 作 AG B
2、C 于 G，过 F 作 FH BC，交 AC 于 H， C30， CH2 F H，设 FH2 a， CH4 a，则 CF2 a， ， BC15 a， CG a， AG a， AC15 a， AH11 a， BAD BDF DHF120， ADB+ FDH ADB+ ABD18012060， ABD FDH， ABD HDF， ，即 ，设 AD x，则 DH11 a x，30 a2 x（11 a x） ，x211 ax+30a20，（ x5 a） （ x6 a）0，x5 a 或 6a， 或 ，故答案为： 或 ；（2）如图 2，过 E 作 EH AB，交 AC 于 H，过 D 作 DM EH 于
3、M，过 F 作 FG ED，交 AC于 G， BE CF， ， ， FG ED， ，设 CG3 a， DG7 a， m， A EDF120， ABC DFE， DEC C， DE DC10 a， FG DE， GFC DEF C， FG CG3 a，同理由（1）得： EHD DFG， ，即 ，DH ，Rt DHM 中， DHM60， HDM30， HM DH ， DM a， EM a， EH a a a， m 2定义：在一个三角形中，若存在两条边 x 和 y，使得 y x2，则称此三角形为“平方三角形” ， x 称为平方边（1） “若等边三角形为平方三角形，则面积为 是 真 命题；“有一个角为
4、 30且有一条直角边为 2 的直角三角形是平方三角形”是 假 命题；（填“真”或“假” ）（2）若 a， b， c 是平方三角形的三条边，平方边 a2，若三角形中存在一个角为 60，求 c 的值；（3）如图，在 ABC 中， D 是 BC 上一点若 CAD B， CD1，求证， ABC 是平方三角形；若 C90， BD1， AC m， CD n，求 tan DAB （用含 m， n 的代数式表示）解：（1）等边三角形为平方三角形，根据平方三角形的定义可知：等边三角形的边长为 1，等边三角形的面积 ，是真命题当直角三角形中，30所对的直角边为 2 时，斜边为 4，满足平方三角形的定义，当直角三角
5、形中，和 30相邻的直角边是 2 时，不是平方三角形，故是假命题，故答案为真，假（2）因为 a， b， c 是平方三角形的三条边，平方边 a2，三角形中存在一个角为 60，只有 B 或 C60， A 不可能为 60，不妨设 B60， BC2，如图 1 中，当 c a2时， a2， c2 24如图 2 中，当 b a24 时，作 CH AB 于 H在 Rt BCH 中， B60， CHB90， BC2， BH BC1， CH BH ，在 Rt ACH 中， AH ， c AB BH+AH1+ ，综上所述， c 的长为 4 或 1+ （3）如图 3 中， C C， CAD B， CAD CBA，
6、， AC2 CDCB， CD1， AC2 BC， ABC 是平方三角形如图 4 中，作 DH AB 于 H在 Rt ABC 中， C90， AC m， BC CD+BD1+ n， AB ， DH AB， DHB90， B B， DHB C90， BHD BCA， ， ， DH ， BH ， AH ，tan DAB 3如图 1，在 ABC 中， AB AC， AD BC 于 D，分别延长 AC 至 E， BC 至 F，且 CE EF，延长 FE 交 A D 的延长线于 G（1）求证： AE EG；（2）如图 2，分别连接 B G， BE，若 BG BF，求证： BE EG；（3）如图 3，取 G
7、F 的中点 M，若 AB5，求 EM 的长证明：（1）如图 1，过 E 作 EH CF 于 H， AD BC， EH AD， CEH CAD， HEF G， CE EF， CEH HEF， CAD G， AE EG；（2）如图 2，连接 GC， AC BC， AD BC， BD CD， AG 是 BC 的垂直平分线， GC GB， GBF BCG， BG BF， GC BE， CE EF， CEF1802 F， BG BF， GBF1802 F， GBF CEF， CEF BCG， BCE CEF+ F， BCE BCG+ GCE， GCE F，在 BEF 和 GCE 中， ， BEF GEC
8、（ SAS） ， BE EG；（3）如图 3，连接 DM，取 AC 的中点 N，连接 DN，由（1）得 AE EG， GAE AGE，在 Rt ACD 中， N 为 AC 的中点， DN AC AN， DAN ADN， ADN AGE， DN GF，在 Rt GDF 中， M 是 FG 的中点， DM FG GM， GDM AGE， GDM DAN， DM AE，四边形 DMEN 是平行四边形， EM DN AC， AC AB5， EM 4 【阅读材料】小明遇到这样一个问题：如图 1，点 P 在等边三角形 ABC 内，且 APC150，PA3， PC4，求 PB 的长小明发现，以 AP 为边作
9、等边三角形 APD，连接 BD，得到 ABD；由等边三角形的性质，可证 ACP ABD，得 PC BD；由已知 APC150，可知 PDB 的大小，进而可求得PB 的长（1）请回答：在图 1 中， PDB 90 ， PB 5 【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图 2， ABC 中， ACB90， AC BC，点 P 在 ABC 内，且PA1， PB ， PC2 ，求 AB 的长【灵活运用】（3）如图 3，在 Rt ABC 中， ACB90， BAC，且 tan ，点 P 在 ABC外，且 PB3， PC1，直接写出 PA 长的最大值解：（1）如图 1 中， ACP AB
10、D， PDB APC150， PC BD4， AD AP3， ADP 为等边三角形， ADP60， DP AD3， BDP1506090， PB 5故答案为：90，5；（2）如图 2 中，把 ACP 绕点 C 逆时针旋转 90得到 BCD由旋转性质可知； BD PA1， CD CP2 ， PCD90， PCD 是等腰直角三角形， PD PC 2 4， CDP45， PD2+BD24 2+1217， PB2（ ） 217， PD2+BD2 PB2， PDB90， BDC135， APC CDB135， CPD45， APC+ CPD180， A， P， D 共线， AD AP+PD5，在 RtA
11、DB 中， AB （3）如图 3 中，作 CD CP，使得 CD PC ，则 PD ，tan BAC ， ， ACB PCD90， ACD BCP， ACD BCP， ， AD ， PA + ， PA ， PA 的最大值为 5一节数学课后，老师布置了一道课后练习： ABC 是等边三角形，点 D 是线段 BC 上的点，点 E 为 ABC 的外角平分线上一点，且 ADE 如图，当点 D 是线段 BC 上（除B， C 外）任意一点时，求证： AD DE（1）理清思路，完成解答本题证明思路可以用下列框图表：根据上述思路，请你完整地书写本题的证明过程；（2）特殊位置，计算求解当点 D 为 BC 的中点时
12、，等边 ABC 的边长为 6，求出 DE 的长；（3）知识迁移，探索新知当点 D 在线段 BC 的延长线上，且满足 CD BC 时若 AB2，请直接写出 ADE 的面积（不必写解答过程）（1）证明：如图中，过点 D 作 DF AC，交 AB 于点 F ABC 是等边三角形， AB BC， B ACB ABC60，又 DF AC， BDF BFD60， BDF 是等边三角形， BF BD， BFD60， AF CD， AFD120， EC 是外角的平分线， DCE120 AFD， ADC 是 ABD 的外角， ADC B+ FAD60+ FAD， ADC ADE+ EDC60+ EDC， FAD
13、 EDC，在 AFD DCE 中， AFD DCE（ ASA） ， AD DE（2）如图中， ABC 是等边三角形， AB AC BC6， BD DC3， AD BC， ADB90， AD 3 ，由（1）可知： DE AD3 （3）如图 3 中， CA CD CB2， BAD90， AD 2 ， ABD DCE， BAD EDC90， ABD60， ADB30， ADE60， AD DE， ADE 是等边三角形， S ADE （2 ） 23 6已知如图 1，在 ABC 中， ACB90， BC AC，点 D 在 AB 上， DE AB 交 BC 于 E，点F 是 AE 的中点（1）线段 FD
14、与线段 FC 的数量关系 DF FC ，位置关系 DF FC ；（2）如图 2，将 BDE 绕点 B 逆时针旋转 a（0 a90） ，其它条件不变，线段 FD与线段 FC 的关系是否变化，写出你的结论并证明；（3）将 BDE 绕点 B 逆时针旋转一周，如果 BC4， BE2 ，直接写出线段 BF 的范围解：（1）如图 1 中， ADE ACE90， AF FE， DF AF EF CF， FAD FDA， FAC FCA， DFE FDA+ FAD2 FAD， EFC FAC+ FCA2 FAC， CA CB， ACB90， BAC45， DFC EFD+ EFC2（ FAD+ FAC）90，
15、 DF FC， DF FC，故答案为： DF FC， DF FC（2）结论不变理由：如图 2 中，延长 AC 到 M 使得 CM CA，延长 ED 到 N，使得 DN DE，连接BN、 BM EM、 AN，延长 ME 交 AN 于 H，交 AB 于 O BC AM， AC CM， BA BM，同法 BE BN， ABM EBN90， NBA EBM， ABN MBE， AN EM， BAN BME， AF FE， AC CM， CF EM， FC EM，同法 FD AN， FD AN， FD FC， BME+ BOM90， BOM AOH， BAN+ AOH90， AHO90， AN MH，
16、FD FC（3）如图 3 中，当点 E 落在 AB 上时， BF 的长最大，最大值3如图 4 中，当点 E 落在 AB 的延长线上时， BF 的值最小，最小值 综上所述， BF3 7 【操作发现】（1）如图 1，将 ABC 绕点 A 逆时针旋转 90得到 ADE，连接 BD，则 ABD 的度数是 45 【类比探究】（2）如图 2，在等腰直角三角形 ABC 内取一点 P，使 APB135，将 ABP 绕顶点 A逆时针旋转 90得到 ACP，连接 PP请猜想 BP 与 CP有怎样的位置关系，并说明理由【解决问题】（3）如图 3，在等腰直角三角形 ABC 内任取一点 P，连接 PA、 PB、 PC求
17、证：PC+ PA PB解：（1）如图 1，由旋转得： BAD90， AB AD， BAD 是等腰直角三角形， ABD45，故答案为：45；（2） BP CP，理由是：如图 2，由旋转得： AB AC， AP AP， BAC PAP90， ABP ACP（ SAS） ， APB APC135， AP AP， PAP90， APP是等腰直角三角形， APP45， APB+ APP180， B、 P、 P三点共线， CPB1354590， BP CP；（3）如图 3，将 ABP 绕点 A 逆时针旋转 90得到 ACP， ACP ABP， PC PB， PA PA，连接 PP， PAP90， PP P
18、A，在 PCP中， PC+PP PC， PC+ PA PB8如图，在平面直角坐标系中，点 A 的坐标为（2，0） ，以线段 OA 为边在第四象限内作等边三角形 AOB，点 C 为 x 正半轴上一动点（ OC2） ，连接 BC，以线段 BC 为边在第四象限内作等边三角形 CBD 连接 DA 并延长交 y 轴于点 E（1）在点 C 的运动过程中， OBC 和 ABD 全等吗？请说明理由；（2）在点 C 的运动过程中， CAD 的度数是否会变化？如果不变，请求出 CAD 的度数；如果变化请说明理由；（3）探究当点 C 运动到什么位置时，以 A， E， C 为顶点的三角形是等腰三角形？解：（1） OB
19、C 和 ABD 全等，理由是： AOB， CBD 都是等边三角形， OB AB， CB DB， ABO DBC， OBC ABD，在 OBC 和 ABD 中， ， OBC ABD（ SAS） ；（2）点 C 在运动过程中， CAD 的度数不会发生变化，理由如下： AOB 是等边三角形， BOA OAB60， OBC ABD， BAD BOC60， CAD180 OAB BAD60；（3） OBC ABD， BOC BAD60，又 OAB60， OAE180606060， EAC120， OEA30，以 A， E， C 为顶点的三角形是等腰三角形时， AE 和 AC 是腰，点 A 的坐标为（2，
20、0） ， OA2，在 Rt AOE 中， OEA30， AE4， AC AE4， OC2+46，当点 C 的坐标为（6，0）时，以 A， E， C 为顶点的三角形是等腰三角形9如图 1， ABC 中， CD AB 于 D，且 BD： AD： CD2：3：4（1）试说明 ABC 是等腰三角形；（2）已知 S ABC40 cm2，如图 2，动点 M 从点 B 出发以每秒 1cm 的速度沿线段 M 向点A 运动，同时动点 N 从点 A 出发以相同速度沿线段 AC 向点 C 运动，当其中一点到达终点时整个运动都停止，设点 M 运动的时间为 t（秒） 若 DMN 的边与 BC 平行，求 t 的值；在点
21、M、 N 运动的过程中， AMN 能否成为直角三角形？若能，直接写出 t 的值；若不能，请说明理由解：（1）设 BD2 x， AD3 x， CD4 x，则 AB5 x，在 Rt ACD 中， AC 5 x， AB AC， ABC 是等腰三角形；（2） S ABC 5x4x40 cm2，而 x0， x2 cm，则 BD4 cm， AD6 cm， CD8 cm， AC10 cm当 MN BC 时， AM AN，即 10 t t， t5；当 DN BC 时， AD AN，得： t6；若 DMN 的边与 BC 平行时， t 值为 5 或 6由题意知 AM AD DM6 t， AN t，如图 1，当 A
22、MN90时， AMN ADC，则 ，即 ，解得： t ；如图 2，当 ANM90时， AMN ACD，则 ，即 ，解得： t ；综上， t 或 时， AMN 是直角三角形10在 ABC 中， AB AC10，sin BAC ，过点 C 作 CD AB，点 E 在边 AC 上，AE CD，联结 AD， BE 的延长线与射线 CD、射线 AD 分别交于点 F、 G设 CD x， CEF的面积为 y（1）求证： ABE CAD（2）如图，当点 G 在线段 AD 上时，求 y 关于 x 的函数解析式及定义域（3）若 DFG 是直角三角形，求 CEF 的面积解：（1） CD AB， BAC ECD，又
23、AE CD， AB AC， DAC EBA（ SAS） ， ABE CAD；（2）过点 E 作 EH AB，垂足为 H，由题意知 CE AC AE10 x， EH AEsin CAB x， AH x，则 S ABE ABEH 10 x3 x， CF BA， CEF AEB， （ ） 2，即 ， y （0 x5 5） ；（3）由于 DFG EBA ABC，所以 DFG 不可能为直角，当 DGF90时， EGA90，由 GAE GBA 知 GAE GBA，tan GBA ，在 Rt EHB 中，tan GBA ， ，解得： x0（舍）或 x5， S CEF 15；当 GDF90时， BAG90，由
24、知 GAE GBA，则 AEB GEA90， BE ABsin BAC10 6， AE 8， CE AC AE2，由 CEF AEB 知 ，即 ，则 EF ， S CEF EFCE 2 ，综上所述，若 DFG 是直角三角形，则 CEF 的面积为 15 或 11已知：等边三角形 ABC（1）如图 1， P 为等边 ABC 内一点，且 PAE 为等边三角形，则 BP EC（填“” ，“”或“” ）（2）如图 2， P 为等边 ABC 外一点，且 BPC120试猜想线段 BP、 PC、 AP 之间的数量关系，并证明你的猜想；（3）如图 3， P 为等边 ABC 内一点，且 APD120求证： PA+
25、PD+PC BD解：（1） APE 为等边三角形， AP AE， PAE60， ABC 为等边三角形， AC BC， BCA60 BAP CAE ABP ACE（ SAS） BP CE，故答案为： （2）猜想： AP BP+PC，证明：延长 BP 至 E，使 PE PC，连接 CE， BPC120 CPE60又 PE PC， CPE 为等边三角形， CP PE CE， PCE60， ABC 为等边三角形， AC BC， BCA60 ACB PCE ACB+ BCP PCE+ BCP ACP BCE， ACP BCE（ SAS） AP BE， BE BO+PE AP BP+PC（3）在 AD 外
26、侧作等边 ABD，则点 P 在三角形 ABD 外，连接 PB， BC， APD120由（1）得 PB AP+PD，在 PBC 中，有 PB+PC CB， PA+PB+PC CB， ABD、 ABC 是等边三角形， AC AB， AB AD BAD CAB ABD ACB（ SAS） CB BD， PA+PD+PC BD12如图，在 ABC 中，点 D 在边 AB 上，点 E 在边 AC 上， CE BD，连接 CD， BE， BE 与 CD相交于点 F（1）如图 1，若 ACD 为等边三角形，且 CE DF，求 CEF 的度数；（2）如图 2，若 AC AD，求证： EF FB；（3）如图 3
27、，在（2）的条件下，若 CFE45， BCD 的面积为 4，求线段 CD 的长（1）解： CE BD， CE DF， BD DF， DFB B， ACD 为等边三角形， ADC C60， DFB B30， CEF90；（2）证明：作 BG AC 交 CD 的延长线于 G， C G， AC AD， C ADC， BDG G， BD BG， CE BD， BD CE， BG AC，在 CFE 和 GFB 中， CFE GFB， EF FB；（3）解：作 EP CD 于 P， BH CD 交 CD 的延长线于 H，设 EP x， GH a， CFE45， FP EP x， CFE GFB， BH EP x，则 FH BH x， BD BG， BH CD， DH GH a， CF FG x+a， DF x a， CD CF+DF2 x，由题意得， CDBH4，即 2xx4，解得， x2，则 CD2 x4
