1、2018-2019 学年河南省郑州市中原区枫杨外国语中学八年级（下）第一次月考数学试卷一、选择题（每题 3 分，共 30 分）1（3 分）下列不等式变形中，错误的是（ ）A若 ab，则 a+cb+c B若 a+cb+c，则 abC若 ab，则 ac2bc 2 D若 ac2 bc2，则 ab2（3 分）如图所示，下列四个图案中，是中心对称图形的有（ ）A1 个 B2 个 C3 个 D4 个3（3 分）用反证法证明：“一个三角形中至多有一个角不小于 90”时，应假设（ ）A一个三角形中至少有两个角不小于 90B一个三角形中至多有一个角不小于 90C一个三角形中至少有一个角不小于 90D一个三角形中
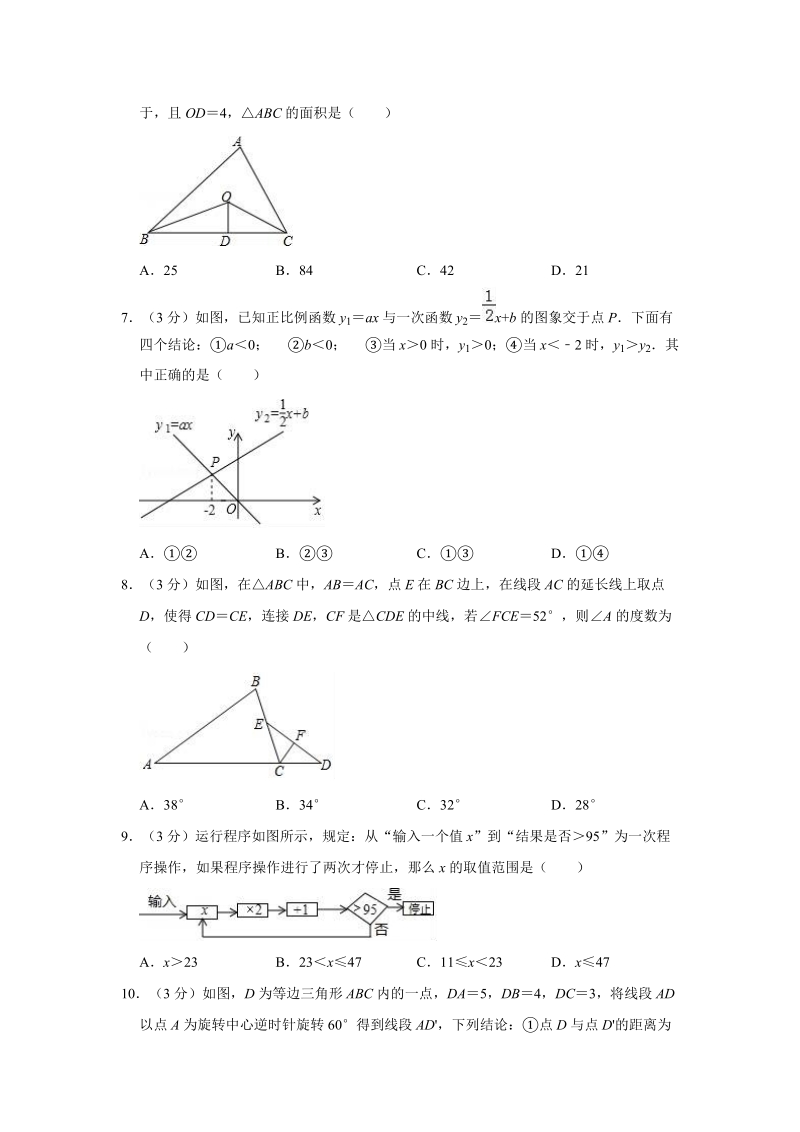
2、没有一个角不小于 904（3 分）下列命题：若|a| b|，则 ab；若 a+b0，则|a| b|；等边三角形的三个内角都相等线段垂直平分线上的点到线段两个端点的距离相等以上命题的逆命题是真命题的有（ ）A0 个 B1 个 C2 个 D3 个5（3 分）关于 x 的不等式组 有四个整数解，则 a 的取值范围是（ ）A a B a C a D a6（3 分）如图，已知ABC 的周长是 21，OB ，OC 分别平分ABC 和ACB，ODBC于，且 OD4，ABC 的面积是（ ）A25 B84 C42 D217（3 分）如图，已知正比例函数 y1ax 与一次函数 y2 x+b 的图象交于点 P下面有
3、四个结论：a0； b0； 当 x0 时，y 1 0； 当 x2 时，y 1y 2其中正确的是（ ）A B C D8（3 分）如图，在ABC 中，ABAC ，点 E 在 BC 边上，在线段 AC 的延长线上取点D，使得 CDCE，连接 DE，CF 是CDE 的中线，若FCE52，则A 的度数为（ ）A38 B34 C32 D289（3 分）运行程序如图所示，规定：从“输入一个值 x”到“结果是否95”为一次程序操作，如果程序操作进行了两次才停止，那么 x 的取值范围是（ ）Ax23 B23x47 C11x23 Dx 4710（3 分）如图，D 为等边三角形 ABC 内的一点，DA5，DB 4，D
4、C3，将线段 AD以点 A 为旋转中心逆时针旋转 60得到线段 AD，下列结论：点 D 与点 D的距离为5； ADC 150； ACD可以由ABD 绕点 A 逆时针旋转 60得到；点 D到 CD的距离为 3；S 四边形 ADCD 6+ ，其中正确的有（ ）A2 个 B3 个 C4 个 D5 个二、填空题（每题 3 分，共 24 分）11（3 分）不等式 5（x2）6+2x 的正整数解共有 个12（3 分）等腰三角形的周长为 13cm，其中一边长为 3cm，则底边长等于 cm13（3 分）某次知识竞赛试卷有 20 道题，评分办法是答对一道记 5 分，不答记 0 分，答错一道扣 2 分，小明有 3
5、 道题没答，但成绩超过 60 分，则小明至少答对 道题14（3 分）若不等式组 的解集为1x1，那么（a+1 ）（b1）的值等于 15（3 分）若不等式 无解，则实数 a 的取值范围是 16（3 分）如图，在平面直角坐标系中，点 A 的坐标为（0，3），OAB 沿 x 轴向右平移后得到OAB，点 A 的对应点 A在直线 y x 上，则点 B 与其对应点 B间的距离为 17（3 分）已知 CD 是ABC 的边 AB 上的高，若 CD ，AD1，AB 2AC ，则 BC的长为 18（3 分）如图，在平面直角坐标系中，A（0，2），B（0，6），动点 C 在直线 yx上若以 A、B、C 三点为顶点的
6、三角形是等腰三角形，则点 C 的个数是 三、解答题（共 5 大题，共 46 分）19（8 分）解不等式组 ，并把它的解集在数轴上表示出来20（9 分）已知方程组 的解满足 x 为非正数，y 为负数（1）求 m 的取值范围；（2）化简：|m3| |m+2|；（3）在 m 的取值范围内，当 m 为何整数时，不等式 2mx+x2m+1 的解为 x121（9 分）如图，ABC 是边长为 6 的等边三角形，P 是 AC 边上一动点，由 A 向 C 运动（与 A、C 不重合），Q 是 CB 延长线上一动点，与点 P 同时以相同的速度由 B 向CB 延长线方向运动（Q 不与 B 重合），过 P 作 PEAB
7、 于 E，连接 PQ 交 AB 于 D（1）若 AE1 时，求 AP 的长；（2）当BQD30时，求 AP 的长；（3）在运动过程中线段 ED 的长是否发生变化？如果不变，求出线段 ED 的长；如果发生变化，请说明理由22（10 分）我市某镇组织 20 辆汽车装运完 A、B、C 三种脐橙共 100 吨到外地销售按计划，20 辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满根据下表提供的信息，解答以下问题：脐 橙 品 种 A B C每辆汽车运载量（吨） 6 5 4每吨脐橙获得（百元） 12 16 10（1）设装运 A 种脐橙的车辆数为 x，装运 B 种脐橙的车辆数为 y，求 y 与 x 之
8、间的函数关系式；（2）如果装运每种脐橙的车辆数都不少于 4 辆，那么车辆的安排方案有几种？并写出每种安排方案；（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值23（10 分）在ABC，BAC 为锐角，ABAC ，AD 平分BAC 交 BC 于点 D（1）如图 1，若ABC 是等腰直角三角形，直接写出线段 AC，CD ，AB 之间的数量关系；（2）BC 的垂直平分线交 AD 延长线于点 E，交 BC 于点 F如图 2，若 ABE60，判断 AC，CE，AB 之间有怎样的数量关系并加以证明；如图 3，若 AC+AB AE，求BAC 的度数2018-2019 学年河南省郑州市中原
9、区枫杨外国语中学八年级（下）第一次月考数学试卷参考答案与试题解析一、选择题（每题 3 分，共 30 分）1（3 分）下列不等式变形中，错误的是（ ）A若 ab，则 a+cb+c B若 a+cb+c，则 abC若 ab，则 ac2bc 2 D若 ac2 bc2，则 ab【分析】根据不等式的基本性质进行答题【解答】解：A、在不等式 ab 的两边同时加 c，不等式仍然成立，即 a+cb+c故本选项不符合题意；B、在不等式 a+cb+c 的两边同时减去 c，不等式仍然成立，即 ab故本选项不符合题意；C、当 c0 时，不等式 ac2bc 2 不成立，故本选项符合题意；D、在不等式 ac2bc 2 的两
10、边同时除以 c2，不等式仍然成立，即 ab故本选项不符合题意故选：C【点评】主要考查了不等式的基本性质（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变（2）不等式两边乘（或除以）同一个正数，不等号的方向不变（3）不等式两边乘（或除以）同一个负数，不等号的方向改变2（3 分）如图所示，下列四个图案中，是中心对称图形的有（ ）A1 个 B2 个 C3 个 D4 个【分析】根据正多边形的性质和轴对称图形与中心对称图形的定义解答【解答】解：是中心对称图形的有：（1）（2）故选：B【点评】此题考查正多边形对称性关键要记住偶数边的正多边形既是轴对称图形，又是中心对称图形，奇数边的正多边形只是
11、轴对称图形3（3 分）用反证法证明：“一个三角形中至多有一个角不小于 90”时，应假设（ ）A一个三角形中至少有两个角不小于 90B一个三角形中至多有一个角不小于 90C一个三角形中至少有一个角不小于 90D一个三角形中没有一个角不小于 90【分析】反证法的步骤中，第一步是假设结论不成立，反面成立，可据此进行判断【解答】解：用反证法证明：“一个三角形中至多有一个角不小于 90”时，应假设一个三角形中至少有两个角不小于 90，故选：A【点评】本题考查的是反证法，解此题关键要懂得反证法的意义及步骤在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情
12、况，则必须一一否定4（3 分）下列命题：若|a| b|，则 ab；若 a+b0，则|a| b|；等边三角形的三个内角都相等线段垂直平分线上的点到线段两个端点的距离相等以上命题的逆命题是真命题的有（ ）A0 个 B1 个 C2 个 D3 个【分析】先得出命题的逆命题，进而判断即可【解答】解：若|a| b|，则 ab 逆命题是若 ab，则|a| b|，如果 a1，b3，则不成立，是假命题；若 a+b0，则|a| |b|逆命题是若|a| b|，则 a+b0，也可能 ab0，是假命题；等边三角形的三个内角都相等逆命题是三个内角都相等的三角形是等边三角形，是真命题线段垂直平分线上的点到线段两端的距离相等
13、的逆命题是到线段两端的距离相等的点在线段垂直平分线上，是真命题；故选：C【点评】主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题判断命题的真假关键是要熟悉课本中的性质定理5（3 分）关于 x 的不等式组 有四个整数解，则 a 的取值范围是（ ）A a B a C a D a【分析】先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求 a 的取值范围即可【解答】解：由得 x8；由得 x24a；关于 x 的不等式组 有四个整数解，其解集为 8x24a，且四个整数解为 9，10，11，12，则 ，解得 a 故选：B【点评】考查不等式组的解法及整数解的确定求不等式组的解集，应遵
14、循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了6（3 分）如图，已知ABC 的周长是 21，OB ，OC 分别平分ABC 和ACB，ODBC于，且 OD4，ABC 的面积是（ ）A25 B84 C42 D21【分析】连接 OA，作 OEAB 于 E，OF AC 于 F，如图，利用角平分线的性质得到ODOE OF 4，然后根据三角形面积公式得到ABC 的面积S AOB +SBOC +SAOC 4（AB+BC+ AC），再把三角形的周长代入计算即可【解答】解：连接 OA，作 OEAB 于 E，OF AC 于 F，如图，OB，OC 分别平分ABC 和ACB，ODOE 4 ，ODO
15、F 4 ，ABC 的面积SAOB +SBOC +SAOC OEAB+ ODBC+ OFAC 4（AB+BC+ AC） 42142故选：C【点评】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等这里的距离是指点到角的两边垂线段的长7（3 分）如图，已知正比例函数 y1ax 与一次函数 y2 x+b 的图象交于点 P下面有四个结论：a0； b0； 当 x0 时，y 1 0； 当 x2 时，y 1y 2其中正确的是（ ）A B C D【分析】根据正比例函数和一次函数的性质判断即可【解答】解：因为正比例函数 y1ax 经过二、四象限，所以 a0，正确；一次函数 y2 x+b 经过一、二、
16、三象限，所以 b0，错误；由图象可得：当 x0 时，y 10，错误；当 x2 时，y 1y 2， 正确；故选：D【点评】此题考查一次函数与一元一次不等式，关键是根据正比例函数和一次函数的性质判断8（3 分）如图，在ABC 中，ABAC ，点 E 在 BC 边上，在线段 AC 的延长线上取点D，使得 CDCE，连接 DE，CF 是CDE 的中线，若FCE52，则A 的度数为（ ）A38 B34 C32 D28【分析】利用等腰三角形的三线合一求出ECD，再求出ACB 即可解决问题【解答】解：CECD，FEFD ，ECFDCF52，ACB18010476，ABAC，BACB76，A18015228，
17、故选：D【点评】本题考查等腰三角形的性质，三角形的内角和定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型9（3 分）运行程序如图所示，规定：从“输入一个值 x”到“结果是否95”为一次程序操作，如果程序操作进行了两次才停止，那么 x 的取值范围是（ ）Ax23 B23x47 C11x23 Dx 47【分析】根据运行程序，第一次运算结果小于等于 95，第二次运算结果大于 95 列出不等式组，然后求解即可【解答】解：由题意得， ，解不等式 得， x47，解不等式 得， x23，23x47，故选：B【点评】本题考查了一元一次不等式组的应用，读懂题目信息，理解运行程序并列出不等式组是解题的关
18、键10（3 分）如图，D 为等边三角形 ABC 内的一点，DA5，DB 4，DC3，将线段 AD以点 A 为旋转中心逆时针旋转 60得到线段 AD，下列结论：点 D 与点 D的距离为5； ADC 150；ACD可以由ABD 绕点 A 逆时针旋转 60得到；点 D到 CD的距离为 3；S 四边形 ADCD 6+ ，其中正确的有（ ）A2 个 B3 个 C4 个 D5 个【分析】连结 DD，根据旋转的性质得 ADAD ，DAD60，可判断ADD 为等边三角形，则 DD5，可对 进行判断；由ABC 为等边三角形得到ABAC，BAC60，则把 ABD 逆时针旋转 60后，AB 与 AC 重合，AD 与
19、 AD重合，于是可对进行判断；再根据勾股定理的逆定理得到DDC 为直角三角形，则可对进行判断；由于 S 四边形 ADCD S ADD +SDDC ，利用等边三角形的面积公式和直角三角形面积公式计算后可对进行判断【解答】解：连结 DD，如图，线段 AD 以点 A 为旋转中心逆时针旋转 60得到线段 AD，ADAD ，DAD 60，ADD 为等边三角形，DD5，所以正确；ABC 为等边三角形，ABAC， BAC60，把ABD 逆时针旋转 60后，AB 与 AC 重合，AD 与 AD重合，ACD可以由ABD 绕点 A 逆时针旋转 60得到，所以正确；DCDB4，DC3，在DDC 中，3 2+425
20、2，DC 2+DC 2DD 2，DDC 为直角三角形，DCD90，ADD 为等边三角形，ADD 60 ，ADC150，所以错误；DCD90，DCCD ，点 D 到 CD的距离为 3，所以正确；S ADD +SDDC 52+ 346+ ，所以 错误故选：B【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角也考查了等边三角形的判定与性质以及勾股定理的逆定理二、填空题（每题 3 分，共 24 分）11（3 分）不等式 5（x2）6+2x 的正整数解共有 5 个【分析】先解不等式，再找不等式的正整数解即可【解答】解：去括号得，5x10
21、6+2x，移项得，5x2x 6+10 ，合并同类项得，3x16，系数化为 1 得，x ，正整数解有：5，4，3，2，1，共 5 个数故答案为 5【点评】本题考查了正确求不等式的正整数解，求出解集是解答本题的关键解不等式应根据不等式的基本性质12（3 分）等腰三角形的周长为 13cm，其中一边长为 3cm，则底边长等于 3 cm【分析】分 3cm 长的边是腰和底边两种情况进行讨论即可求解【解答】解：当长是 3cm 的边是底边时，三边为 3cm，5cm，5cm ，等腰三角形成立；当长是 3cm 的边是腰时，底边长是：13337cm，而 3+37，不满足三角形的三边关系故底边长是：3cm故答案为：3
22、【点评】本题主要考查了等腰三角形的计算，正确理解分两种情况讨论，并且注意到利用三角形的三边关系定理，是解题的关键13（3 分）某次知识竞赛试卷有 20 道题，评分办法是答对一道记 5 分，不答记 0 分，答错一道扣 2 分，小明有 3 道题没答，但成绩超过 60 分，则小明至少答对 14 道题【分析】设小明答对了 x 道题，则答错了（203x）道题，根据总分5答对题目数2答错题目数结合成绩超过 60 分，即可得出关于 x 的一元一次不等式，解之即可得出 x 的取值范围，再取其中最小正整数即可得出结论【解答】解：设小明答对了 x 道题，则答错了（203x）道题，依题意，得：5x2（203x）60
23、，解得：x13 x 为正整数，x 的最小值为 14故答案为：14【点评】本题考查了一元一次不等式的应用，根据各数量之间的关系，正确列出一元一次不等式是解题的关键14（3 分）若不等式组 的解集为1x1，那么（a+1 ）（b1）的值等于 6 【分析】先用字母 a，b 表示出不等式组的解集 2b+3x ，然后再根据已知解集是1x1，对应得到相等关系 2b+31， 1，求出 a，b 的值再代入所求代数式中即可求解【解答】解：解不等式组 可得解集为 2b+3x 因为不等式组的解集为1x1，所以 2b+31， 1，解得 a1，b2 代入（a+1）（b1）2（3）6故答案为：6【点评】主要考查了一元一次不
24、等式组的解定义，解此类题是要先用字母 a，b 表示出不等式组的解集，然后再根据已知解集，对应得到相等关系，解关于字母 a，b 的一元一次方程求出字母 a，b 的值，再代入所求代数式中即可求解15（3 分）若不等式 无解，则实数 a 的取值范围是 a1 【分析】先把 a 当作已知条件求出不等式的解集，再根据不等式组无解即可得出 a 的取值范围【解答】解： ，由 得，x a，由得，x1，不等式组无解，a1，解得 a1故答案为：a1【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”是解答此题的关键16（3 分）如图，在平面直角坐标系中，点 A 的坐标为
25、（0，3），OAB 沿 x 轴向右平移后得到OAB，点 A 的对应点 A在直线 y x 上，则点 B 与其对应点 B间的距离为 4 【分析】根据平移的性质知 BBAA由一次函数图象上点的坐标特征可以求得点A的坐标，所以根据两点间的距离公式可以求得线段 AA的长度，即 BB的长度【解答】解：如图，连接 AA、BB点 A 的坐标为（0，3），OAB 沿 x 轴向右平移后得到O AB，点 A的纵坐标是 3又点 A 的对应点在直线 y x 上一点，3 x，解得 x4点 A的坐标是（4，3），AA4根据平移的性质知 BBAA4故答案为 4【点评】本题考查了一次函数图象上点的坐标特征、坐标与图形变化平移根
26、据平移的性质得到 BBAA 是解题的关键17（3 分）已知 CD 是ABC 的边 AB 上的高，若 CD ，AD1，AB 2AC ，则 BC的长为 2 或 2 【分析】分两种情况：当 ABC 是锐角三角形，如图 1，当 ABC 是钝角三角形，如图 2，分别根据勾股定理计算 AC 和 BC 即可【解答】解：分两种情况：当 ABC 是锐角三角形，如图 1，CDAB ，CDA90，CD ，AD1，AC2，AB2AC，AB4，BD413，BC 2 ；当 ABC 是钝角三角形，如图 2，同理得：AC2，AB4，BC 2 ；综上所述，BC 的长为 2 或 2 故答案为：2 或 2 【点评】本题考查了三角形
27、的高、勾股定理的应用，在直角三角形中常利用勾股定理计算线段的长，要熟练掌握18（3 分）如图，在平面直角坐标系中，A（0，2），B（0，6），动点 C 在直线 yx上若以 A、B、C 三点为顶点的三角形是等腰三角形，则点 C 的个数是 3 【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得 AB 的垂直平分线与直线 yx 的交点为点 C，再求出 AB 的长，以点 A 为圆心，以 AB 的长为半径画弧，与直线 yx 的交点为点 C，求出点 B 到直线 yx 的距离可知以点 B 为圆心，以 AB 的长为半径画弧，与直线没有交点【解答】解：如图，AB 的垂直平分线与直线 yx 相交于点 C1
28、，A（0，2），B（0，6），AB624，以点 A 为圆心，以 AB 的长为半径画弧，与直线 yx 的交点为 C2，C 3，OB6，点 B 到直线 yx 的距离为 6 3 ，3 4，以点 B 为圆心，以 AB 的长为半径画弧，与直线 yx 没有交点，所以，点 C 的个数是 1+23故答案为 3【点评】本题考查了等腰三角形的判定，坐标与图形性质，作出图形，利用数形结合的思想求解更形象直观三、解答题（共 5 大题，共 46 分）19（8 分）解不等式组 ，并把它的解集在数轴上表示出来【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集【
29、解答】解：解不等式 1 ，得：x ，解不等式 x5 （3x 2），得： x ，则不等式组的解集为 x ，将解集表示在数轴上如下：【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键20（9 分）已知方程组 的解满足 x 为非正数，y 为负数（1）求 m 的取值范围；（2）化简：|m3| |m+2|；（3）在 m 的取值范围内，当 m 为何整数时，不等式 2mx+x2m+1 的解为 x1【分析】首先对方程组进行化简，根据方程的解满足 x 为非正数，y 为负数，就可以得出 m 的范围，然后再化简（
30、2），最后求得 m 的值【解答】解：（1）解原方程组得： ，x0，y0， ，解得2m3；（2）|m 3| |m+2|3m m212m；（3）解不等式 2mx+x2m+1 得，（2m+1 ）x 2m+1，x1，2m+1 0，m ，2m ， m1【点评】主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）21（9 分）如图，ABC 是边长为 6 的等边三角形，P 是 AC 边上一动点，由 A 向 C 运动（与 A、C 不重合），Q 是 CB 延长线上一动点，与点 P 同时以相同的速度由 B 向CB 延长线方向
31、运动（Q 不与 B 重合），过 P 作 PEAB 于 E，连接 PQ 交 AB 于 D（1）若 AE1 时，求 AP 的长；（2）当BQD30时，求 AP 的长；（3）在运动过程中线段 ED 的长是否发生变化？如果不变，求出线段 ED 的长；如果发生变化，请说明理由【分析】（1）根据等边三角形的性质得到A60，根据三角形内角和定理得到APE 30，根据直角三角形的性质计算；（2）过 P 作 PFQC ，证明DBQDFP，根据全等三角形的性质计算即可；（3）根据等边三角形的性质、直角三角形的性质解答【解答】解：（1）ABC 是等边三角形，A60，PEAB，APE 30，AE1，APE30，PEA
32、B，AP2AE2；（2）解：过 P 作 PFQC ，则AFP 是等边三角形，P、Q 同时出发，速度相同，即 BQAP，BQPF，在DBQ 和 DFP 中，DBQ DFP，BDDF ，BQD BDQFDP FPD30，BDDF FA AB2，AP2；（3）解：由（2）知 BDDF，AFP 是等边三角形，PEAB，AEEF，DEDF +EF BF+ FA AB3 为定值，即 DE 的长不变【点评】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质以及平行线的性质，掌握全等三角形的判定定理和性质定理是解题的关键22（10 分）我市某镇组织 20 辆汽车装运完 A、B、C 三种脐橙共 100
33、吨到外地销售按计划，20 辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满根据下表提供的信息，解答以下问题：脐 橙 品 种 A B C每辆汽车运载量（吨） 6 5 4每吨脐橙获得（百元） 12 16 10（1）设装运 A 种脐橙的车辆数为 x，装运 B 种脐橙的车辆数为 y，求 y 与 x 之间的函数关系式；（2）如果装运每种脐橙的车辆数都不少于 4 辆，那么车辆的安排方案有几种？并写出每种安排方案；（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值【分析】（1）等量关系为：车辆数之和20；（2）关系式为：装运每种脐橙的车辆数4；（3）总利润为：装运 A 种脐橙的车辆数
34、612+装运 B 种脐橙的车辆数516+装运C 种脐橙的车辆数410，然后按 x 的取值来判定【解答】解：（1）根据题意，装运 A 种脐橙的车辆数为 x，装运 B 种脐橙的车辆数为y，那么装运 C 种脐橙的车辆数为（ 20x y），则有：6x+5y+4（20x y ） 100整理得：y2x +20（1x 9 且为整数）；（2）由（1）知，装运 A、B、C 三种脐橙的车辆数分别为 x，2x+20，x由题意得：解得：4x8因为 x 为整数，所以 x 的值为 4，5，6，7，8，所以安排方案共有 5 种方案一：装运 A 种脐橙 4 车，B 种脐橙 12 车，C 种脐橙 4 车；方案二：装运 A 种脐
35、橙 5 车，B 种脐橙 10 车，C 种脐橙 5 车，方案三：装运 A 种脐橙 6 车，B 种脐橙 8 车，C 种脐橙 6 车，方案四：装运 A 种脐橙 7 车，B 种脐橙 6 车，C 种脐橙 7 车，方案五：装运 A 种脐橙 8 车，B 种脐橙 4 车，C 种脐橙 8 车；（3）设利润为 W（百元）则： W6x12+5（2x +20） 16+4x1048x+1600k480W 的值随 x 的增大而减小要使利润 W 最大，则 x4，故选方案一 W 最大 484+16001408（百元）14.08（万元）答：当装运 A 种脐橙 4 车，B 种脐橙 12 车，C 种脐橙 4 车时，获利最大，最大利
36、润为14.08 万元【点评】解决本题的关键是读懂题意，根据关键描述语，找到所求量的等量关系确定x 的范围，得到装在的几种方案是解决本题的关键23（10 分）在ABC，BAC 为锐角，ABAC ，AD 平分BAC 交 BC 于点 D（1）如图 1，若ABC 是等腰直角三角形，直接写出线段 AC，CD ，AB 之间的数量关系；（2）BC 的垂直平分线交 AD 延长线于点 E，交 BC 于点 F如图 2，若 ABE60，判断 AC，CE，AB 之间有怎样的数量关系并加以证明；如图 3，若 AC+AB AE，求BAC 的度数【分析】（1）ABAC+CD，理由为：过 D 作 DE 垂直于 AB，利用角平
37、分线定理得到DCDE，进而利用 HL 得到三角形 ACD 与三角形 AED 全等，利用全等三角形对应边相等得到 ACAE，再由三角形 ABC 为等腰直角三角形得到三角形 BDE 为等腰直角三角形，即 DEEB ，由 ABAE+EB，等量代换即可得证；（2） ABAC +CE，理由为：在线段 AB 上截取 AHAC，连接 EH，由 AD 为角平分线得到一对角相等，再由 ACAH，AEAE，利用 SAS 得到三角形 ACE 与三角形 AHE全等，得到 CEHE，由 EF 垂直平分 BC，得到 CEBE，根据ABE60，得到EHB 是等边三角形，进而得到 BHHE ，由 ABAH +HB，等量代换即
38、可得证；在线段 AB 上截取 AHAC，连接 EH，作 EMAB 于点 M同理可得ACEAHE，得到 CEHE ，进而确定出EHB 是等腰三角形，得到 HMBM，根据AC+ABAH+ ABAM HM+AM+MB2AM，将已知等式 AC+AB AE，代入得：AM AE，在 RtAEM 中，利用锐角三角函数定义求出 cosEAM 的值，进而确定出EAB 30，即可得到CAB 的度数【解答】解：（1）ABAC+CD，理由为：过 D 作 DEAB ，如图 1 所示，AD 平分BAC，DCAC，CDDE，在 Rt ACD 和 RtAED 中，RtACD RtAED（HL ），ACAE，ABC 为等腰直角
39、三角形，B45，即BDE 为等腰直角三角形，CDDEEB，则 ABAE+EBAC+ CD；（2） ABAC +CE；证明：在线段 AB 上截取 AHAC，连接 EH，如图 2 所示，AD 平分BAC，CAEBAE，在ACE 和AHE 中，ACEAHE（SAS），CEHE，EF 垂直平分 BC，CEBE，又ABE 60，EHB 是等边三角形，BHHE ，ABAH +HBAC+CE；在线段 AB 上截取 AHAC，连接 EH，作 EMAB 于点 M如图 3 所示，同理可得ACEAHE，CEHE，EHB 是等腰三角形，HM BM，AC+ABAH+ABAM HM+AM+MB2AM，AC+AB AE，AM AE，在 Rt AEM 中， cosEAM ，EAB 30CAB2EAB60【点评】此题考查了全等三角形的判定与性质，线段垂直平分线定理，等腰直角三角形，以及解直角三角形，熟练掌握全等三角形的判定与性质是解本题的关键
