1、 - 1 - 高中数学必修 4 知识点 第一章 三角函数 正 角 : 按 逆 时 针 方 向 旋 转 形 成 的 角1 、 任 意 角 负 角 : 按 顺 时 针 方 向 旋 转 形 成 的 角零 角 : 不 作 任 何 旋 转 形 成 的 角2、 象限的角 ： 在直角坐标系内，顶点与原点重合，始边与 x 轴的非负半轴重合，角的终边落在第几象限，就是第几象限的角；角的终边落在坐标轴上，这个角不属于任何象限，叫做 轴线角 。 第一象限角的集合为 3 6 0 3 6 0 9 0 ,k k k 第二象限角的集合为 3 6 0 9 0 3 6 0 1 8 0 ,k k k 第三象限角的集合为 3 6
2、0 1 8 0 3 6 0 2 7 0 ,k k k 第四象限 角的集合为 3 6 0 2 7 0 3 6 0 3 6 0 ,k k k 终边在 x 轴上的角的集合为 1 8 0 ,kk 终边在 y 轴上的角的集合为 1 8 0 9 0 ,kk 终边在坐标轴上的角的集合为 9 0 ,kk 3、 与 角 终边相同的角，连同角 在内，都可以表示为集合 Zkk ,360| 4、 弧度制 ： （ 1）定义：等于半径的弧所对的圆心角叫做 1 弧度的角，用弧度做单位叫弧度制。 半径为 r 的圆的圆心角 所对弧的长为 l ，则角 的弧度数的绝对值是 lr （ 2） 度数与弧度数的换算 ： 2360o ， 1
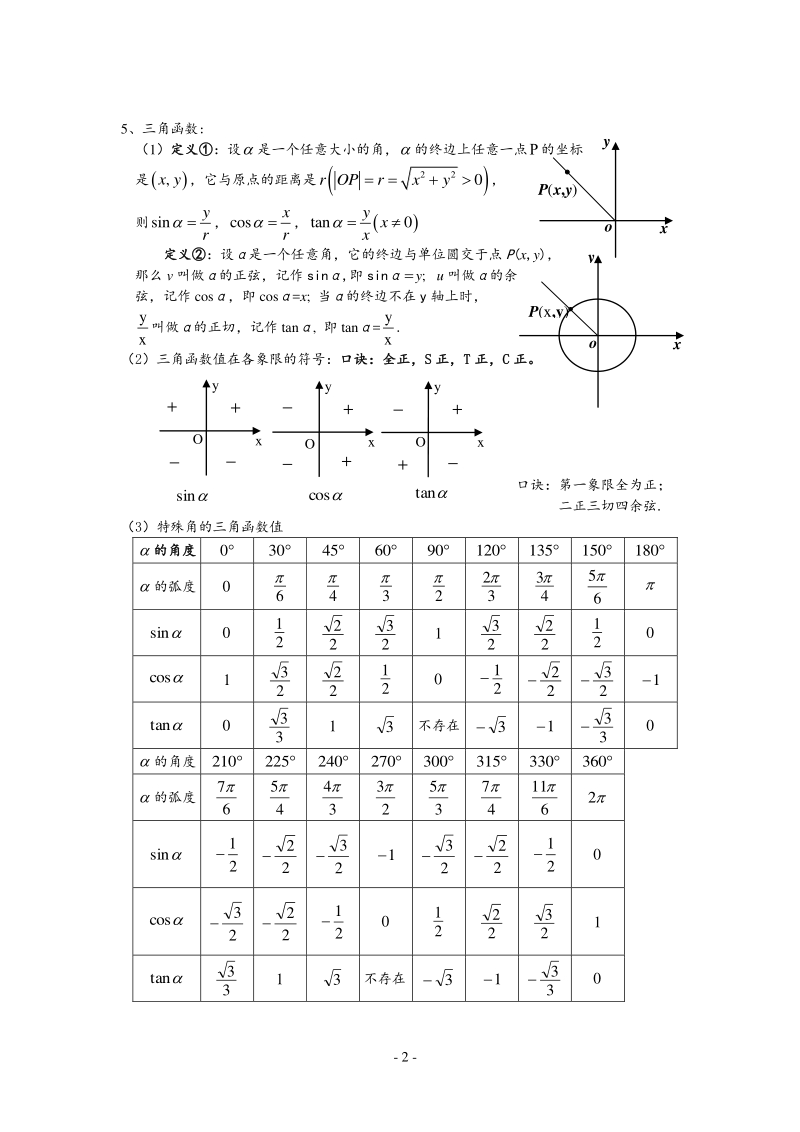
3、80 rad， 1 rad 185730.57)180( 注： 角度与弧度的相互转化：设一个角的角度为 on ，弧度为 ； 角度化为弧度： 180180 nnn ooo ，弧度化为角度： oo 180180 （ 3）若扇形的圆心角为 （ 是角的弧度数），半径为 r ，则： 弧长公式： ,180 （用度表示的）nl （用弧度表示的）rl | ； 扇形面积： )(360 2 用度表示的扇 rns lrrS 21|21 2 扇（用弧度表示的） - 2 - 5、 三角函数 : （ 1） 定义 ： 设 是一个任意大小的角， 的终边上任意一点 的坐标 是 ,xy ，它与原点的距离是 22 0r O P r
4、 x y ， 则 sin yr ， cos xr ， tan 0y xx 定义 ： 设 是一个任意角，它的终边与单位圆交于点 P(x,y)， 那么 v 叫做 的正弦，记作 sin ,即 sin y; u 叫做 的余 弦，记作 cos ，即 cos =x; 当 的终边不在 y 轴上时， xy 叫做 的正切，记作 tan , 即 tan =xy . （ 2）三角函数值在各象限的符号： 口诀：全正， S 正， T 正， C 正。 口诀：第一象限全为正； 二正三切四余弦 . （ 3）特殊角的三角函数值 的角度 0 30 45 60 90 120 135 150 180 的弧度 0 6 4 3 2 32
5、 43 65 sin 0 21 22 23 1 23 22 21 0 cos 1 23 22 21 0 21 22 23 1 tan 0 33 1 3 不存在 3 1 33 0 的角度 210 225 240 270 300 315 330 360 的弧度 67 45 34 23 35 47 611 2 sin 21 22 23 1 23 22 21 0 cos 23 22 21 0 21 22 23 1 tan 33 1 3 不存在 3 1 33 0 P(x,y) yxosin x y + + _ _ O x y + + _ _ cos O tan x y + + _ _ O P(x,y)
6、yxo- 3 - （ 4）三角函数线：如下图 （ 5）同角三角函数基本关系式 （）平方关系： 1cossin 22 （）商数关系： cossintan 6、三角函数的诱导公 式： 1 s in 2 s ink ， co s 2 co sk ， t a n 2 t a nkk 口诀：终边相同的角的同一三角函数值相等 2 sin sin ， cos cos ， tan tan 3 sin sin ， co s co s ， tan tan 4 s in s in ， co co s ， tan tan 5 s in 2 s in ， cos 2 cos ， tan 2 tan 口诀：函数名称不变，
7、正负看象限 6 s in c o s2 ， cos sin2 ， ta n cot2 7 s in c o s2 ， c o s sin2 ， ta n c o t2 口诀：正弦与余弦互换，正负看象限 诱导公式记忆口诀：“奇变偶不变，符号看象限” 。 即将括号里面的角拆成 2k的形式。 - 4 - 7、 正弦函数、余弦函数和正切函数的图象与性质： 函数 sinyx cosyx tanyx 图 象 定义域 R R ,2x x k k 值 域 值域： 1,1 当 2 2xk k 时，max 1y ；当 2 2xk k 时， min 1y 值域： 1,1 当 2x k k 时， max 1y ；当
8、2xk k 时， min 1y 值域： R 既无最大值也无最小值 周期性 sinyx 是周期函数；周期为2,T k k Z且 0k ； 最小正周期为 2 cosyx 是周期函数；周期为 2,T k k Z且 0k ； 最小正周期为 2 tanyx 是周期函数；周期为 ,T k k Z且0k ；最小正周期为 奇偶性 奇函 数 偶函数 奇函数 单调性 在 2 , 222kk k 上是增函数；在 32 , 222kk k 上是减函数 在 2 , 2k k k 上是增函数；在 2 ,2kk k 上是减函数 在 ,22kk k 上是增函数 对称性 对称中心 ,0kk 对称轴 2x k k 对称中心 ,0
9、2kk 对称轴 x k k 对称中心 ,02k k 无对称轴 - 5 - 8、 （ 1） siny x b 的图象与 xy sin 图像的关系： 振幅变换： xy sin xAy sin 周期变换： xy sin xy sin 相位变换： xy sin )sin( xy 平移变换： )sin( xAy siny x b 注：函数 xy sin 的图象怎样变换得到函数 siny A x B 的图象：（两种方法） 先平移后伸缩： sinyx 平移 | 个单位 sinyx （左加右减） 纵坐标不变 )sin( xy 横坐标变为原来的 1|倍 横坐标不变 siny A x 纵坐标变为原来的 A 倍 平
10、移 |B 个单位 s iny A x B （上加下减） 先伸缩后平移： sinyx 纵坐标不变 xy sin 横坐标变为原来的 1|倍 平移 个单位 )sin( xy （左加右减） 横坐标不变 siny A x 纵坐标变为原来的 A 倍 平移 |B 个单位 s iny A x B 图象整体向左 （ 0 ）或向右（ 0 ） 平移 个单位 图象上每个点的横坐标不变，纵坐标变为原来的 A 倍 图象上每个点的横坐标变为原来的 1 倍，纵坐标不变 图象整体向上 （ 0b ）或向下（ 0b ） 平移 b 个单位 - 6 - （上加下减） （ 2）函数 )0,0()s in ( AbxAy 的性质： 振幅：
11、 ； 周期： 2 ； 频率： 1 2f ； 相位： x ； 初相： 定义域： R 值域： ,A b A b 当 2 2xk k 时， maxy A b； 当 2 2xk k 时， miny A b 周期性：函数 )0,0()s in ( AbxAy 是周期函数；周期为 2T 单调性： x 在 2 , 222kk k上时是增函数； x 在 32 , 222kk k 上时是减函数 对称性：对称中心为 ,0k k；对称轴为 x 2kk 第二章 平面向量 1、向量 定义：既有大小又有方向的量叫做向量， 向量都可用同一平面内的有向线段表示 2、零向量： 长度为 0 的向量叫零向量，记作 0 ；零向量的方
12、向是任意的 3、单位向量： 长度等于 1 个单位长度的向量叫单位向量；与向量 a 平行的单位向量：|aae 4、平行向量（共线向量）： 方向相同或相反的非零向量叫平行向量也叫共线向量，记作 ba/ ； 规定 0 与任何向量平行 5、相等向量： 长度相同且方向相同的向量叫相等向量，零向量与零向量相等 . 注意： 任意两个相等的非零向量，都可以用同一条有向线段来表示，并且与有向线段的起点无关。 6、向量加法运算： 三角形法则的特点： 首尾相接 平行四边形法则的特点： 起点相同 b a C a b C C - 7 - 运算性质： 交换律： a b b a ； 结合律： a b c a b c ； 0
13、0a a a 坐标运算：设 11,a x y ， 22,b x y ，则 1 2 1 2,a b x x y y 7、向量减法运算： 三角形法则的特点：共起点，连终点，方向指向被减向量 坐标运算：设 11,a x y ， 22,b x y ，则 1 2 1 2,a b x x y y 设 、 两点的坐标分别为 11,xy ， 22,xy ，则 2 1 2 1,x x y y 8、向量数乘运算： 实数 与向量 a 的积是一个向量的运算叫做向量的数乘，记作 a aa ； 当 0 时， a 的方向与 a 的方向相同；当 0 时， a 的方向与 a 的方向相反； 当 0 时， 0a 运算律： aa ；
14、 a a a ； a b a b 坐标运算：设 ,a x y ，则 ,a x y x y 9、向量共线定理：向量 0aa 与 b 共线，当且仅当有唯一一个实数 ，使 ba 设 11,a x y ， 22,b x y ，其中 0b ，则当且仅当 1 2 2 1 0x y x y时，向量 a 、 0bb共线 10、平面向量基本定理：如果 1e 、 2e 是同一平面内的两个不共线向量，那么对于这一平面内的任意向量 a ，有且只有一对实数 1 、 2 ，使 1 1 2 2a e e（ 不共线 的向量 1e 、 2e 作为这一平面内所有向量的一组基底） 11、分点坐标公式 ：设点 是线段 12 上的一点
15、， 1 、 2 的坐标分别是 11,xy ， 22,xy ，当 12 时，点 的坐标是 1 2 1 2,11x x y y 12、平面向量的数量积： - 8 - 定义： c o s 0 , 0 , 0 1 8 0a b a b a b 零向量与任一向量的数量积为 0 性质：设 a 和 b 都是非零向量，则 0a b a b 当 a 与 b 同向时， a b a b ；当 a 与 b 反向时， a b a b ； 22a a a a 或 a a a a b a b 运算律： a b b a ； a b a b a b ； a b c a c b c 坐标运算：设两个非零向量 11,a x y ，
16、 22,b x y ，则 1 2 1 2a b x x y y 若 ,a x y ，则 2 22a x y，或 22a x y 设 11,a x y ， 22,b x y ，则 1 2 1 2 0a b x x y y 设 a 、 b 都是非零向量， 11,a x y ， 22,b x y ， 是 a 与 b 的夹角，则 1 2 1 22 2 2 21 1 2 2c o sx x y yababx y x y 第三章 三角恒等变形 1、 同角三角函数基本关系式 （）平方关系： 1cossin 22 （ ）商数关系： cossintan （）倒数关系： 1cottan 222 tan1 tans
17、in ； 22 t an1 1co s 注意： tan,cos,sin 按照以上公式可以“知一求二” 2、 两角和与差的正弦、余弦、正切 )( S ： s i nc o sc o ss i n)s i n ( )( S ： s i nc o sc o ss i n)s i n ( )( C ： s i ns i nc o sc o s)c o s ( a )( C ： s i ns i nc o sc o s)c o s ( a )( T ： t a nt a n1 t a nt a n)t a n ( )( T ： t a nt a n1 t a nt a n)t a n ( 正切和公式：
18、)t a nt a n1()t a n (t a nt a n - 9 - 3、 辅助角公式 ： xba bxba abaxbxa c o ss i nc o ss i n 222222)s i n ()s i nc o sc o s( s i n 2222 xbaxxba （其中 称为辅助角， 的终边过点 ),( ba ， abtan ） 4、二倍角的正弦、余弦和正切公式： 2S ： co ssin22sin 2C ： 22 s inc o s2c o s 1c o s2s in21 22 2T ： 2tan1 tan22tan *二倍角公式的常用变形： 、 |s in|22c o s1 ，
19、 |c o s|22c o s1 ； 、 |s in|2c o s2121 ， |c o s|2c o s2121 2 2s i n1c o ss i n21c o ss i n 22244 ； 2c o ss inc o s 44 ； *降次公式： 2s in21co ss in 212c o s212 2c o s1s i n 2 212c o s212 2c o s1c o s 2 5、 *半角 的正弦、余弦和正切公式 ： 2co s12s in ； 2co s12co s ， co s1 co s12t an co s1 s ins inco s1 6、 同角三角函数的常见变形：（活用
20、“ 1”） 22 cos1sin ； 2cos1sin ； 22 sin1cos ； 2sin1cos ； 2s i n2c o ss i n s i nc o sc o tt a n 22 ，- 10 - 2c o t22s i n 2c o s2c o ss i n s i nc o st a nc o t 22 2s i n1c o ss i n21)c o s( s i n 2 ； |c o ss in|2s in1 7、 补充公式： 万能公式 2tan12tan2sin2 ； 2t a n12t a n1c o s22 ； 2t an12t an2t an2 积化和差公式 )s i n () s i n (21c o ss i n )s i n () s i n (21s i nc o s )c o s () c o s (21c o sc o s )c o s () c o s (21s i ns i n 和差化积公式 2c o s2s i n2s i ns i n ； 2s i n2c o s2s i n 2c o s2c o s2c o sc o s ； 2s i n2s i n2c o sc o s 注： 带 *号的公式表示了解，没带 *公式为必记公式
