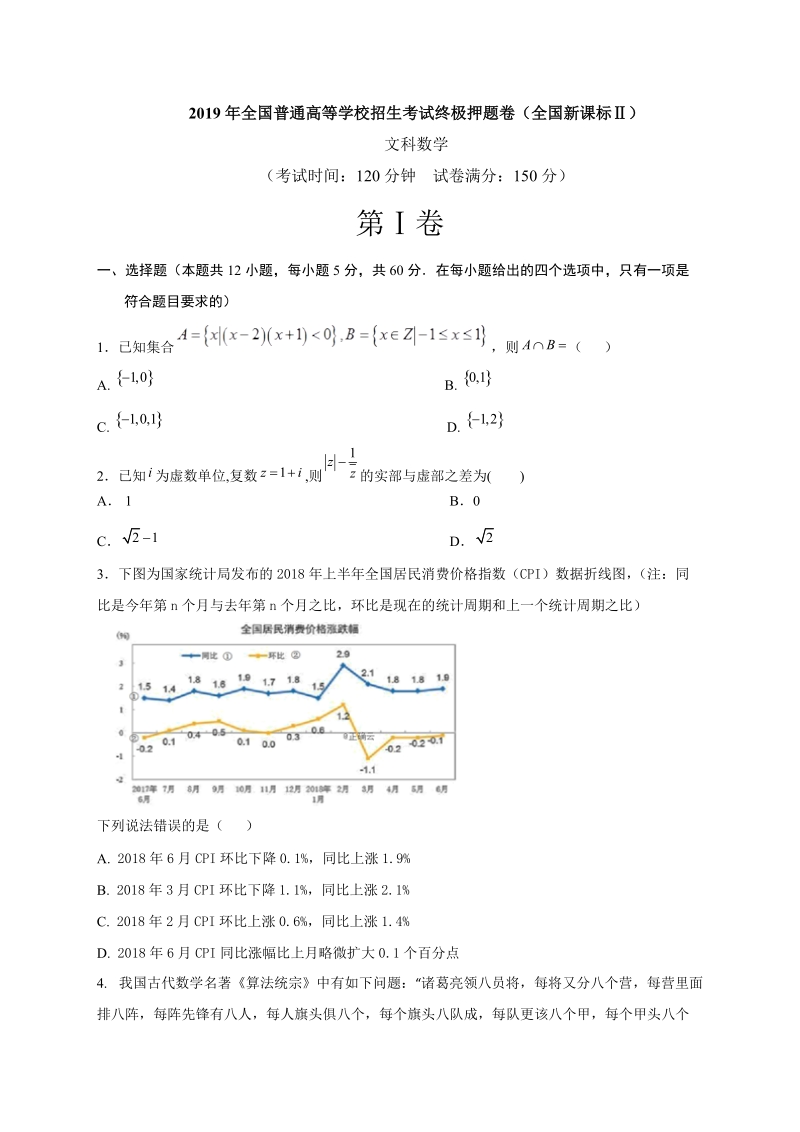
1、2019 年全国普通高等学校招生考试终极押题卷（全国新课标）文科数学（考试时间：120 分钟 试卷满分：150 分）第卷一、选择题（本题共 12 小题，每小题 5 分，共 60 分在每小题给出的四个选项中，只有一项是符合题目要求的）1已知集合 ，则 （ ）ABA. B. ,0 0,1C. D. , ,22已知 为虚数单位,复数 ,则 的实部与虚部之差为( )i 1zizA 1 B0C D 23下图为国家统计局发布的 2018 年上半年全国居民消费价格指数（CPI）数据折线图， （注：同比是今年第 n 个月与去年第 n 个月之比，环比是现在的统计周期和上一个统计周期之比）下列说法错误的是（ ）A
2、. 2018 年 6 月 CPI 环比下降 0.1%，同比上涨 1.9%B. 2018 年 3 月 CPI 环比下降 1.1%，同比上涨 2.1%C. 2018 年 2 月 CPI 环比上涨 0.6%，同比上涨 1.4%D. 2018 年 6 月 CPI 同比涨幅比上月略微扩大 0.1 个百分点4. 我国古代数学名著算法统宗中有如下问题：“诸葛亮领八员将，每将又分八个营，每营里面排八阵，每阵先锋有八人，每人旗头俱八个，每个旗头八队成，每队更该八个甲，每个甲头八个兵 ”则该问题中将官、先锋、旗头、队长、甲头、士兵共有（ ）A 人 B 人718 9187C 人 D 人 45程序框图如下图所示，若上
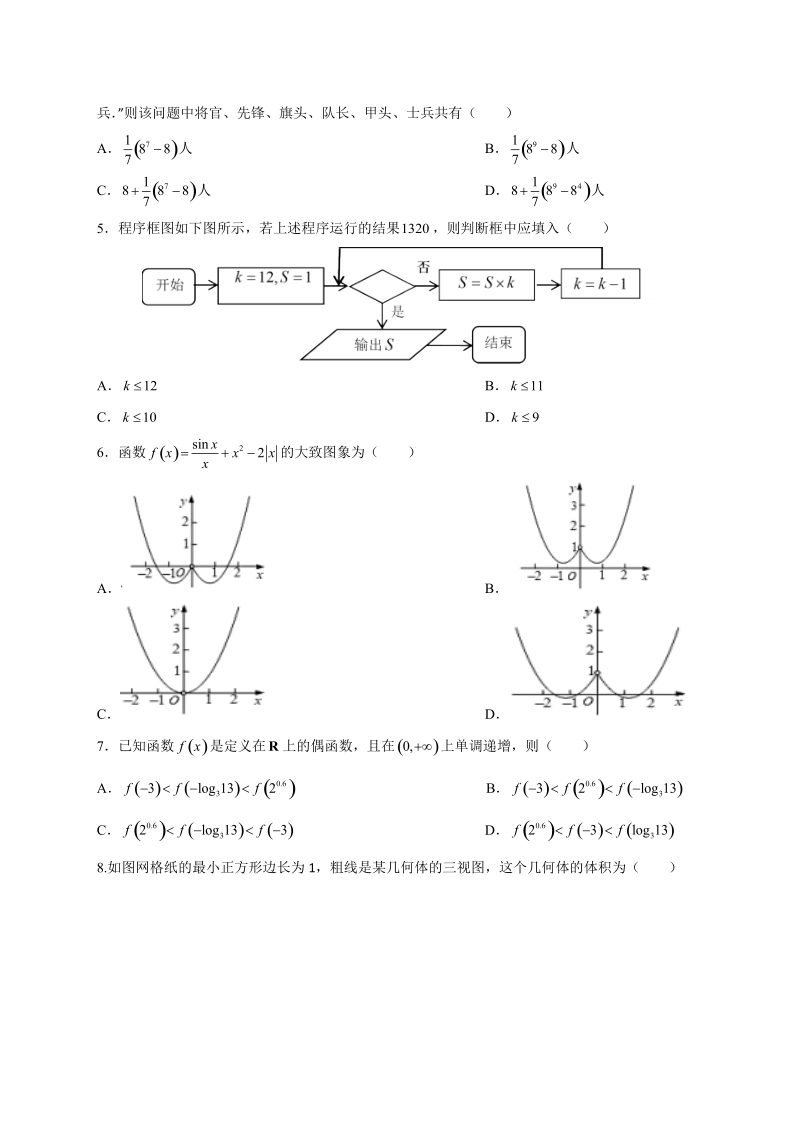
3、述程序运行的结果 ，则判断框中应填入（ ）1320A B12k 1kC D0 96函数 的大致图象为（ ）2sinxfA B C D7已知函数 是定义在 上的偶函数，且在 上单调递增，则（ ）fxR0,A B0.63log12fff 0.6332log1fffC D0.62lfff 0.6lfff8.如图网格纸的最小正方形边长为 1，粗线是某几何体的三视图，这个几何体的体积为（ ）A32 B 643C D 8XXK329. 设点 ， 分别为椭圆 的左、右焦点，点 是椭圆 上任意一点，若使得1F22:195xyCPC成立的点恰好是 个，则实数 的值可以是（ ）12Pm4mA B 3C D5 81
4、0若 是方程 的解， 是方程 的解，则 （ ）1x1xe2xln1x12xA B C De e11. 某人 5 次上班图中所花的时间（单位：分钟）分别为 ，已知这组数据的平均数为,910,xy10，方差为 2，则 =（ ）xyA B1 2C D3 412. 在三棱锥 中， 底面 ， ， ， ，则此三棱锥的外DABCABC5A4C接球的表面积为（ ）A B30 32C D4 6第卷二、填空题（本题共 4 小题，每小题 5 分，共 20 分）13若实数 满足 ,则 的最大值为_,xy0261yx2zxy14. 甲、乙、丙三位同学获得某项竞赛活动的前三名，但具体名次未知，3 人作出如下预测：甲说：我
5、不是第三名；乙说：我是第三名；丙说：我不是第一名；若甲、乙、丙三位同学的预测有且只有一个正确，由此判断获得第一名的同学是_15. 已知变量 ， ，且 ，若 恒成立，则 的最大值为1x20,m12x21xm_16. 在矩形 中， ， ， 为 边上的中点， 为线段 上的动点，设向量ABCDADECPAE，则 的最大值为_ P三、解答题（共 70 分解答应写出必要的文字说明、证明过程或演算步骤。第 1721 题为必考题，每个试题考生都必须作答，第 22、23 题为选考题，考生根据要求作答。 ）（一）必考题：共 60 分。17 （本小题满分 12 分）各项均为整数的等差数列 ，其前 项和为 ， ， ，
6、 ， 成等比数列nanS1a23a41S（）求 的通项公式；na（）求数列 的前 项和 1n22nT18 （本小题满分 12 分）某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数 与烧开一壶水所用时间 的一组数据，且作了一定的数据处理(如下表) ，得到了散点图(如xy下图):表中 ， 21iiwx10iw（）根据散点图判断， 与 哪一个更适宜作烧水时间 关于开关旋钮旋转的弧yabx2dycxy度数 的回归方程类型?( 不必说明理由 )x（）根据判断结果和表中数据，建立 关于 的回归方程；y（）若旋转的弧度数 与单位时间内煤气输出量 成正比，那么 为多少
7、时，烧开一壶水最省煤xtx气？附：对于一组数据 ， ， ， ， ，其回归直线 的斜率和截距的最1,uv2,3,uv,nvu小二乘估计分别为 ， 21niiiu19 （本小题满分 12 分）如图，在四棱锥 中， ， ， ，且 ，PABCDPADBC 22PCBADC2PA（）证明： 平面 ；（）在线段 上，是否存在一点 ，使得二面角 的大小为 ？如果存在，求MAD60的值；如果不存在，请说明理由MPD20 （本小题满分 12 分）已知椭圆 经过点 ，且右焦点 2:10xyEab13,2P23,0F（）求椭圆 的方程；（）若直线 与椭圆 交于 ， 两点，当 最大时，求直线 的方程:2lykxEAB
8、Al21 （本小题满分 12 分）已知函数 eln1xf（）求函数 在点 处的切线方程；yf,f（）证明： 3fx（二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题计分。选修 4-4：坐标系与参数方程（10 分）22 （本小题满分 10 分）在平面直角坐标系中，直线 的参数方程为 （ 为参数， ） 以坐标原点为极点，l cosinxtyt0轴正半轴为极轴建立极坐标系，曲线 的极坐标方程为 x C24cos2in（）写出曲线 的直角坐标方程；C（）若直线 与曲线 交于 ， 两点，且 的长度为 ，求直线 的普通方程lABA25l选修 4-5：不等式选讲
9、 （10 分）23. 已知函数 ， 21fxmxR（）当 时，解不等式 ；1f（）若不等式 对任意 恒成立，求实数 的取值范围3fx0,1xm2019 年全国普通高等学校招生考试终极押题卷（全国新课标）文科数学（考试时间：120 分钟 试卷满分：150 分）注意事项： 1本试卷分第卷（选择题）和第 卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2回答第卷时，选出每小题答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。3回答第 卷时，将答案写在答题卡上。写在本试卷上无效。4考试结束后，将本试卷和答
10、题卡一并交回。第卷一、选择题（本题共 12 小题，每小题 5 分，共 60 分在每小题给出的四个选项中，只有一项是符合题目要求的）1已知集合 ，则 （ ）ABA. B. ,0 0,1C. D. , ,2【答案】B【解析】 ， ，则，故选 B. 2已知 为虚数单位,复数 ,则 的实部与虚部之差为( )i 1zizA 1 B0C D2 2【答案】D【解析】：复数 ，1zi112,2,2-=2izi实 部 ， 虚 部 ， 实 部 虚 部【点评】：该小题几乎考查了复数部分的所有概念,是一道优秀试题。3下图为国家统计局发布的 2018 年上半年全国居民消费价格指数（CPI）数据折线图， （注：同比是今年
11、第 n 个月与去年第 n 个月之比，环比是现在的统计周期和上一个统计周期之比）下列说法错误的是（ ）A. 2018 年 6 月 CPI 环比下降 0.1%，同比上涨 1.9%B. 2018 年 3 月 CPI 环比下降 1.1%，同比上涨 2.1%C. 2018 年 2 月 CPI 环比上涨 0.6%，同比上涨 1.4%D. 2018 年 6 月 CPI 同比涨幅比上月略微扩大 0.1 个百分点【答案】CXXK【分析】对照表中数据逐项检验即可.【详解】观察表中数据知 A,B,D 正确，对选项 C，2018 年 2 月 CPI 环比上涨 2.9%，同比上涨 1.2%，故 C 错误，故选：C【点睛
12、】本题考查折线图，准确识图读图理解题意是关键，是基础题.4. 我国古代数学名著算法统宗中有如下问题：“诸葛亮领八员将，每将又分八个营，每营里面排八阵，每阵先锋有八人，每人旗头俱八个，每个旗头八队成，每队更该八个甲，每个甲头八个兵 ”则该问题中将官、先锋、旗头、队长、甲头、士兵共有（ ）A 人 B 人718 9187C 人 D 人 4【答案】D【解析】由题意可得将官、营、阵、先锋、旗头、队长、甲头、士兵依次成等比数列，且首项为8，公比也是 8，所以将官、先锋、旗头、队长、甲头、士兵共有：，故选 D4545678 941875程序框图如下图所示，若上述程序运行的结果 ，则判断框中应填入（ ）132
13、0A B12k 1kC D0 9【答案】D【解析】初始值， ；12,ks执行框图如下： ；不能满足条件，进入循环； ；不能满足条件，进, 132,0sk入循环； ；此时要输出，因此要满足条件，故选 D1320,9sk6函数 的大致图象为（ ）inxfA BC D【答案】D【解析】 ，排除 B，C ，1sin2si10f当 时， ，则 时， ， ，排除 A，故选 D0x4437已知函数 是定义在 上的偶函数，且在 上单调递增，则（ ）fR0,A B0.63log12fff 0.6332log1fffC D0.62lfff0.6lfff【答案】C【解析】根据题意，函数 是定义在 上的偶函数，则 ，
14、fxR3ff，有 ，又由 在 上单调递增，则有33log1lff0.6332log1l27fx0,，故选 C0.62lfff8.如图网格纸的最小正方形边长为 1，粗线是某几何体的三视图，这个几何体的体积为（ ）A32 B 643C D 832【答案】B【解析】由题意，根据给定的三视图可知，该几何体表示底面是边长为 4 的正方形，高为 4 的四棱锥，该四棱锥的体积为 ，故选 B164339. 设点 ， 分别为椭圆 的左、右焦点，点 是椭圆 上任意一点，若使得1F22:195xyCPC成立的点恰好是 个，则实数 的值可以是（ ）12Pm4mA B 3C D5 8【答案】B【解析】点 ， 分别为椭圆
15、 的左、右焦点；1F22:195xyC即 ， ， ， ， ， ，12,0,a2b24c设 ， ， ，0,Pxy10,2xy20,PFxy由 可得 ，12Fm4又 在椭圆上，即 ， ，20195xy209mx要使得 成立的点恰好是 个，则 ，解得 ，12P49415m 的值可以是 3故选 Bm10若 是方程 的解， 是方程 的解，则 （ ）1x1xe2xln1x12xA B C De e【答案】A【解析】： ， ，设 与 分别交于1xxe1lnlxxylnxey和,由对称性得 ,故选 A.12(,)()AxBx21212ABkxx11. 某人 5 次上班图中所花的时间（单位：分钟）分别为 ，已知
16、这组数据的平均数为,90y10，方差为 2，则 =（ ）xyA B1 2C D3 4【答案】D【解析】：这是一道最新数学素养考题的体现，据题意有 ，按一般同220(1)()8xy学的常规思路解出 ，导致运算量大而出错，其实由点到直线的距离公式知：,xy xy代表直线 与圆 的交点到直线 的距离的2xy2022(1)(0)8xy0倍，所以 = 。故选 D.xy4xyrA12. 在三棱锥 中， 底面 ， ， ， ，则此三棱锥的外DBCBCA5BD4C接球的表面积为A B3032C D4 6【答案】:C【解析】：由题意，在三棱锥 中， 底面 ，ABCABC， ， ，AB5D4可得 ，故三棱锥 的外接
17、球的半径 ，则其表23CD22343R面积为 故选 C .24第 卷二、填空题（本题共 4 小题，每小题 5 分，共 20 分）13若实数 满足 ,则 的最大值为_,xy0261yx2zxy【答案】：2【解析】：作出线性可行域如图，当 y=2x 过点 A（2,2）时，纵截距最小，此时 z 最大，最大值为.14. 甲、乙、丙三位同学获得某项竞赛活动的前三名，但具体名次未知，3 人作出如下预测：甲说：我不是第三名；乙说：我是第三名；丙说：我不是第一名；若甲、乙、丙三位同学的预测有且只有一个正确，由此判断获得第一名的同学是_【答案】：乙【解析】：甲、乙、丙的排名及预测对错如下表：甲 对、错 乙 对、
18、错 丙 对、错1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 所以满足条件的甲、乙、丙排名依次为第三名，第一名，第二名，故答案为乙。15. 已知变量 ， ，且 ，若 恒成立，则 的最大值为1x20,m12x21xm_【答案】： e【解析】 ，即 化为 ，故 在 上为增函数，21x212lnlx12lnxlnxf0,，故 的最大值为 .2ln0efme16. 在矩形 中， ， ， 为 边上的中点， 为线段 上的动点，设向量ABCD21ADECPAE，则 的最大值为_ P【答案】2【解析】以 为原点， ， 所在直线为 ， 轴建立平面直角坐标系，ABAxy则 ， ， ，2,0
19、B,1D,E设 ， ， ， ， ，,Pxy2,1B0,1AD,Pxy ， ， ，AB,xy2 ， ，故答案为 223x2x三、解答题（共 70 分解答应写出必要的文字说明、证明过程或演算步骤。第 1721 题为必考题，每个试题考生都必须作答，第 22、23 题为选考题，考生根据要求作答。 ）（一）必考题：共 60 分。17 （本小题满分 12 分）各项均为整数的等差数列 ，其前 项和为 ， ， ， ， 成等比数列nanS1a23a41S（1）求 的通项公式；na（2）求数列 的前 项和 1n22nT【答案】 （1） ；（2） 3na【解析】 （1）由题意，可知数列 中， ， ， ， 成等比数列
20、，na12a341S则 ，即 ，解得 ，数列的通项公234aS216dd式 6 分23na（2）由（1） ，可知 ， .12na2123421n nTaaa12 分18 （本小题满分 12 分）某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数 与烧开一壶水所用时间 的一组数据，且作了一定的数据处理(如下表) ，得到了散点图(如xy下图)表中 ， 21iiwx10iw（1）根据散点图判断， 与 哪一个更适宜作烧水时间 关于开关旋钮旋转的弧yabx2dycxy度数 的回归方程类型?(不必说明理由)x（2）根据判断结果和表中数据，建立 关于 的回归方程；y（
21、3）若旋转的弧度数 与单位时间内煤气输出量 成正比，那么 为多少时，烧开一壶水最省煤气？xtx附：对于一组数据 ， ， ， ， ，其回归直线 的斜率和截距的最1,uv2,3,uv,nvu小二乘估计分别为 ， 21niiiu【答案】 （1） 更适宜；（2） ；（3） 时，煤气用量最小dycx205yx2x【解析】 （1） 更适宜作烧水时间关于开关旋钮旋转的弧度数 的回归方程类2 x型.4 分（2）由公式可得： ，10216.208iiiiiwyd，0.62.785cydw所求回归方程为 8 分25yx（3）设 ，则煤气用量 ，tk202055kkSytkxxx当且仅当 时取“”，即 时，煤气用量
22、最小 .12 分205x19 （本小题满分 12 分）如图，在四棱锥 中， ， ， ，且 ，PABCDPADBC 22PCBADC2PA（1）证明： 平面 ；（2）在线段 上，是否存在一点 ，使得二面角 的大小为 ？如果存在，求MA60的值；如果不存在，请说明理由MPD【答案】 （1）见证明；（2）见解析【解析】 （1）在底面 中， ， ，且 ，ABCDB ADC22BADC ， ， ，又 ， ， 平面 ，2ABC2PPA平面 ， 平面 ，又 平面 ， ， ，PPP2， ，2PCAC又 ， ， 平面 ， 平面 ， 平BABCDABCDPA面 .6 分D（2）方法一：在线段 上取点 ，使 ，则
23、，ADN2ADMNPA又由（1）得 平面 ， 平面 ，PBCMBC又 平面 ， ，作 于 ，ACO又 ， 平面 ， 平面 ， 平面 ，MNOANO又 平面 ， ，又 ， 是二面角 的一个平ACACNMACD面角，设 ，则 ， ，这样，二面角PxD12NxPx2OxAD的大小为 ，即 ，即 ，满MAC60tantan603MN423Px足要求的点 存在，且 12 分423PD方法二：取 的中点 ，则 、 、 三条直线两两垂直BCEADP可以分别以直线 、 、 为 、 、 轴建立空间直角坐标系，xyz且由（1）知 是平面 的一个法向量，0,2APACD设 ，则 ， ，0,1PMxD12NxAPx2
24、NADx ， ，,2Ax,0C设 是平面 的一个法向量，,QabcM则 ， ，20AxcCab 2abxc令 ，则 ，它背向二面角，bx2,Qx又平面 的法向量 ，它指向二面角，AD0,P这样，二面角 的大小为 ，MC6即 ，2221cos cos6022,QxP x 即 ，423x满足要求的点 存在，且 .12 分M423PD20 （本小题满分 12 分）已知椭圆 经过点 ，且右焦点 2:10xyEab13,2P23,0F（1）求椭圆 的方程；（2）若直线 与椭圆 交于 ， 两点，当 最大时，求直线 的方程:2lykxEABAl【答案】 （1） ；（2） 21412yx【解析】 （1）设椭圆
25、 的左焦点 ，则 ，13,0F124aPFa又 ，所以椭圆 的方程为 .4 分223cbacE24xy（2）由 ，设 ， ，2214804ykxkxk 1,A2,Bxy由 ，且 ， ，6 分22186012284kx124k8 分222 211 2844141kABkxxkk设 ，则 ， ，.10 分24tk0,2t2 56664ABtt当 ，即 时， 有最大值 ，此时 .12 分1t151:2lyx21 （本小题满分 12 分）已知函数 eln1xf（1）求函数 在点 处的切线方程；yf,f（2）证明： 3fx【答案】 （1） ；（2）见解析e1y【解析】 （1） ， ，ln0xf1exf又
26、由题意得 ， ， ，e1fe1fy即切线方程为 .6 分2yx（2）证明：由（1）知 ，易知 在区间 单调递增，exffx0,，且 ， ，使得 ，即 有唯一的根，8 分0f10f01,20fx记为 ，则 ，0x0ex对 两边取对数，得 整理得 ，0e01lnlx00lnx 时， ， ，函数 单调递减，0,xhff时， ， ，函数 单调递增，,0xxx ，10 分0 0min 1eln3fxf当且仅当 ，即 时，等号成立，010x ， ，即 .12 分0,2xmin3f3fx（二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题计分。选修 4-4：坐标系
27、与参数方程（10 分）22 （本小题满分 10 分）在平面直角坐标系中，直线 的参数方程为 （ 为参数， ） 以坐标原点为极点，l cosinxtyt0轴正半轴为极轴建立极坐标系，曲线 的极坐标方程为 x C24cos2in（1）写出曲线 的直角坐标方程；C（2）若直线 与曲线 交于 ， 两点，且 的长度为 ，求直线 的普通方程lABA25l【答案】 （1） ；（2） 和 219xy34yx0【解析】 （1）将 代入曲线 极坐标方程得：cosinC曲线 的直角坐标方程为 ，即 .5 分C242xyxy2219xy（2）将直线 的参数方程代入曲线方程： ，l cossintt整理得 ，24cos
28、in40tt设点 ， 对应的参数为 ， ，解得 ， ，AB1t2124cosint124t则 ，212124si65ttt3cosincos0 ， 和 ，直线 的普通方程为 和 03anl4yx010 分选修 4-5：不等式选讲 （10 分）23. 已知函数 ， 21fxmxR（1）当 时，解不等式 ；f（2）若不等式 对任意 恒成立，求实数 的取值范围3fx0,1xm【答案】 （1） ；（2） 402m【解析】 （1）当 时， ， ，m12fxx123,1xf即求不同区间对应解集， 的解集为 .5 分2fx2fx403x（2）由题意， 对任意的 恒成立，3fx0,1即 对任意的 恒成立，21xm,x令 ，1,02343,gxx函数 的图象应该恒在 的下方，数形结合可得 ymg02m.10 分
