1、2018-2019 学年北京四中九年级（下）开学数学试卷一、选择题（每小题 2 分，共 16 分）1（2 分）如图，在 RtABC 中，C90，AC4，tanA ，则 BC 的长度为（ ）A2 B8 C D2（2 分）如图，D，E 为 ABC 的边 AB，AC 上的点，DEBC，若AD：DB1： 3，DE 2，则 BC 的长是（ ）A10 B8 C6 D43（2 分）将二次函数 yx 26x +5 用配方法化成 y（x h） 2+k 的形式，下列结果中正确的是（ ）Ay（x6） 2+5 By（x3） 2+5 Cy（x3） 24 Dy （x+3） 294（2 分）将抛物线 y3x 2 平移，得到
2、抛物线 y3 （x1） 22，下列平移方式中，正确的是（ ）A先向左平移 1 个单位，再向上平移 2 个单位B先向左平移 1 个单位，再向下平移 2 个单位C先向右平移 1 个单位，再向上平移 2 个单位D先向右平移 1 个单位，再向下平移 2 个单位5（2 分）若点 A（2，y 1），B（1，y 2），C（3，y 3）在二次函数 y2x 2+4x1 的图象上，则 y1，y 2，y 3 的大小关系是（ ）Ay 1y 2y 3 By 2y 3y 1 Cy 3y 2y 1 Dy 2y 1y 36（2 分）若一个扇形的半径是 18cm，面积是 54cm2，则扇形的圆心角为（ ）A30 B60 C90
3、 D1207（2 分）如图，AB 是O 的切线，B 为切点，AO 的延长线交O 于 C 点，连接 BC，若A 30，AB 2 ，则 AC 等于（ ）A4 B6 C D8（2 分）二次函数 yax 2+bx+c（a，b，c 为常数，且 a0）中的 x 与 y 的部分对应值如表：x 1 0 1 3 y 1 3 5 3 下列结论：（1）ac0；（2）当 x1 时，y 的值随 x 值的增大而减小（3）3 是方程ax2+（b1）x +c0 的一个根；（4）当1x 3 时，ax 2+（b1）x+c0其中正确的个数为（ ）A1 个 B2 个 C3 个 D4 个二、填空题（每小题 2 分，共 16 分）9（2
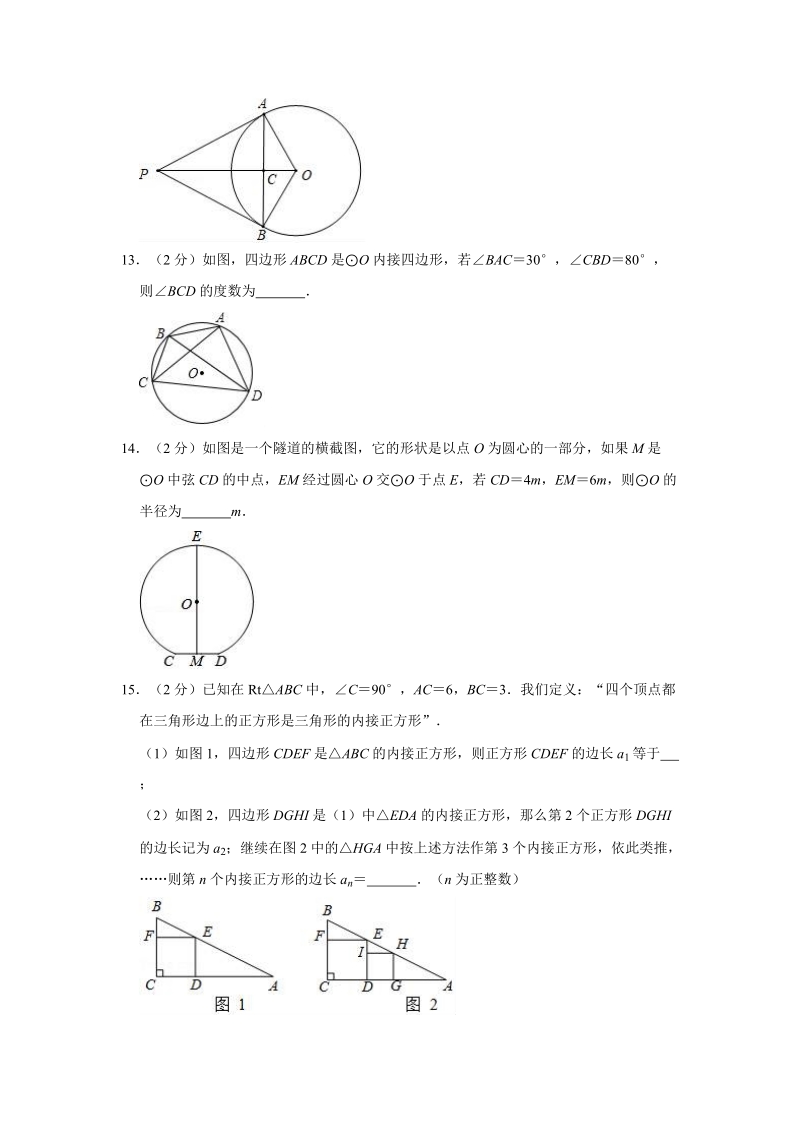
4、 分）若二次函数 yx 2+2x+2k4 的图象与 x 轴有两个交点，则 k 的取值范围为 10（2 分）如图，在平行四边形 ABCD 中，E 为 CD 上一点，连接 AE、BD，且 AE、BD交于点 F，S DEF ：S ABF 4：25，则 DE：EC 11（2 分）请写出一个开口向下，且经过点（1，0）的二次函数的解析式 12（2 分）如图，PA，PB 是 O 的两条切线，切点分别为 A，B连接OA，OB，AB，PO，PO 与 AB 交于点 C若APB60，OC1，则PAB 的周长为 13（2 分）如图，四边形 ABCD 是O 内接四边形，若 BAC30，CBD80，则BCD 的度数为
5、14（2 分）如图是一个隧道的横截图，它的形状是以点 O 为圆心的一部分，如果 M 是O 中弦 CD 的中点，EM 经过圆心 O 交O 于点 E，若 CD4m，EM 6m，则O 的半径为 m15（2 分）已知在 RtABC 中，C90，AC6，BC3我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”（1）如图 1，四边形 CDEF 是ABC 的内接正方形，则正方形 CDEF 的边长 a1 等于 ；（2）如图 2，四边形 DGHI 是（1）中EDA 的内接正方形，那么第 2 个正方形 DGHI的边长记为 a2；继续在图 2 中的HGA 中按上述方法作第 3 个内接正方形，依此类推，
6、则第 n 个内接正方形的边长 an （n 为正整数）16（2 分）如图，RtABC 中，ABBC ，AB6，BC4，P 是ABC 内部的一个动点，且满足PABPBC，则线段 CP 长的最小值为 三、解答题17（5 分）在数学课上，老师提出利用尺规作图完成下面问题：已知：ABC 是O 的内接三角形求作：ABC 中BAC 的平分线小明的作法如下：（1）作 BC 边的垂直平分线 DE，交 BC 于点 D，交弧 BC 于点 E；（2）连接 AE，交 BC 边于点 F；则线段 AF 为所求ABC 中BAC 的平分线根据小明设计的尺规作图过程，（1）在图中补全图形（尺规作图，保留作图痕迹）；（2）完成下面
7、的证明证明：OBOC，DE 是线段 BC 的垂直平分线圆心 O 在直线 DE 上（ ）DEBC， （ ）BAE CAE（ ），线段 AF 为所求ABC 中BAC 的平分线18（5 分）计算：tan60sin 245+tan452cos3019（5 分）如图，四边形 ABCD 各顶点的坐标分别为 A（2，6），B（4，2），C（6，2），D（6，4）（1）在第一象限内，以原点 O 为位似中心，画出四边形 ABCD 的位似图形 A1B1C1D1，使对应边长变为原来的 ；（2）将线段 AB 绕点 B 顺时针旋转 90得到线段 A2B，画出线段 A2B，并计算点 A 所经过的路径长20（5 分）已知抛
8、物线 yx 24x +2（1）此抛物线与 y 轴的交点坐标是 ，顶点坐标是 ；（2）在坐标系中利用描点法画出此抛物线；x y （3）结合图象回答：垂直于 y 轴的直线 l 与抛物线 yx 24x+2 相交于点 P（x 1，y 1），Q（x 2，y 2），则x1+x2 ；若点 A（5， t）和点 B（m，n）都在抛物线 yx 24x+2 上，且 nt，则 m 的取值范围是 21（6 分）如图，在矩形 ABCD 中，AB2，BC4，对角线 AC 与 BD 交于点 O，点 E在 BC 边上，DE 与 AC 交于点 F，CDECBD求：（1）CE 的长；（2）EF 的长22（5 分）已知：如图，斜坡
9、AP 的坡度为 1：2.4，坡长 AP 为 26 米，在坡顶 A 处的同一水平面上有一座古塔 BC，在斜坡底 P 处测得该塔的塔顶 B 的仰角为 45，在坡顶 A处测得该塔的塔顶 B 的仰角为 76求：（1）坡顶 A 到地面 PQ 的距离；（2）古塔 BC 的高度（结果精确到 1 米）（参考数据：sin76 0.97，cos76 0.24，tan764.01）23（5 分）如图，在ABC 中，ACB 90，CD 为 AB 边上的中线，过点 D 作DEBC 于 E，过点 C 作 AB 的平行线与 DE 的延长线交于点 F，连接 BF（1）求证：四边形 BDCF 为菱形；（2）若 CE4，AC6，
10、求四边形 BDCF 的面积24（6 分）如图，在ABC 中，ABAC ，以 AB 为直径的O 分别交 AC，BC 于点D，E，过点 B 作O 的切线，交 AC 的延长线于点 F（1）求证：CBF CAB；（2）连接 BD，AE 交于点 H，若 AB5，tanCBF ，求 BH 的值25（6 分）如图，半圆 O 的直径 AB5cm ，点 M 在 AB 上且 AM1cm ，点 P 是半圆 O上的动点，过点 B 作 BQPM 交 PM（或 PM 的延长线）于点 Q设PMxcm，BQycm（当点 P 与点 A 或点 B 重合时，y 的值为 0）小石根据学习函数的经验，对函数 y 随自变量 x 的变化而
11、变化的规律进行了探究下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：x/cm 1 1.5 2 2.5 3 3.5 4y/cm 0 3.7 3.8 3.3 2.5 （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当 BQ 与直径 AB 所夹的锐角为 60时，PM 的长度约为 cm26（6 分）已知抛物线 yax 2+bx+c 经过点 A（0，3）和 B（4，3）（1）直接写出 a，b 之间的数量关系式： ；（2）若抛物线的顶点在 x 轴上，求 a 的值；（3）若 M（1，0
12、），N（3，0），且抛物线与线段 MN 只有一个公共点，求 a 的取值范围27（7 分）如图 1，在等腰直角ABC 中，ACB 90，P 是射线 CB 上一动点（与点C，B 不重合），连接 AP，延长 BC 至点 Q，使得 CQCP，过点作 QHAP 于点 H，交直线 AB 于点 M在图 1 中补全图形若 PAC，用含 的式子表示AMQ 的大小为AMQ ；探究线段 MB 与 PQ 之间的数量关系，并给出证明28（7 分）在平面直角坐标系 xOy 中， C 的半径为 r，P 是与圆心 C 不重合的点，点 P关于 C 的反称点的定义如下：若在射线 CP 上存在一点 P，满足 CP+CP2r，则称
13、P为点 P 关于 C 的反称点，如图为点 P 及其关于C 的反称点 P的示意图特别地，当点 P与圆心 C 重合时，规定 CP0（1）当O 的半径为 1 时分别判断点 M（2，1），N （ ，0），T（1， ）关于O 的反称点是否存在？若存在，求其坐标；点 P 在直线 yx+2 上，若点 P 关于O 的反称点 P存在，且点 P不在 x 轴上，求点 P 的横坐标的取值范围；（2）C 的圆心在 x 轴上，半径为 1，直线 y x+2 与 x 轴、y 轴分别交于点A，B，若线段 AB 上存在点 P，使得点 P 关于C 的反称点 P在C 的内部，求圆心C 的横坐标的取值范围2018-2019 学年北京四
14、中九年级（下）开学数学试卷参考答案与试题解析一、选择题（每小题 2 分，共 16 分）1（2 分）如图，在 RtABC 中，C90，AC4，tanA ，则 BC 的长度为（ ）A2 B8 C D【分析】根据角的正切值与三角形边的关系求解【解答】解：在 RtABC 中，C90，AC4，tanA ，BC2故选：A【点评】此题考查了解直角三角形的知识，解题的关键是能够选择合适的边角关系求解，难度不大2（2 分）如图，D，E 为 ABC 的边 AB，AC 上的点，DEBC，若AD：DB1： 3，DE 2，则 BC 的长是（ ）A10 B8 C6 D4【分析】利用相似三角形的判定方法证明ADEABC，利
15、用相似三角形的性质得到 ，然后利用比例性质计算出 BC【解答】解：ADBC，ADEABC， ，即 ，BC8故选：B【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形利用相似三角形的性质计算线段的长3（2 分）将二次函数 yx 26x +5 用配方法化成 y（x h） 2+k 的形式，下列结果中正确的是（ ）Ay（x6） 2+5 By（x3） 2+5 Cy（x3） 24 Dy （x+3） 29【分析】运用配方法把一般式化为顶点式即可【解答】解：yx 26x
16、 +5 x26x+94（x3） 24 ，故选：C【点评】本题考查的是二次函数的三种形式，正确运用配方法把一般式化为顶点式是解题的关键4（2 分）将抛物线 y3x 2 平移，得到抛物线 y3 （x1） 22，下列平移方式中，正确的是（ ）A先向左平移 1 个单位，再向上平移 2 个单位B先向左平移 1 个单位，再向下平移 2 个单位C先向右平移 1 个单位，再向上平移 2 个单位D先向右平移 1 个单位，再向下平移 2 个单位【分析】找到两个抛物线的顶点，根据抛物线的顶点即可判断是如何平移得到【解答】解：y3x 2 的顶点坐标为（0，0），y 3（x1） 22 的顶点坐标为（1，2），将抛物线
17、y3x 2 向右平移 1 个单位，再向下平移 2 个单位，可得到抛物线y3（x1） 22故选：D【点评】本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的法则是解答此题的关键5（2 分）若点 A（2，y 1），B（1，y 2），C（3，y 3）在二次函数 y2x 2+4x1 的图象上，则 y1，y 2，y 3 的大小关系是（ ）Ay 1y 2y 3 By 2y 3y 1 Cy 3y 2y 1 Dy 2y 1y 3【分析】求出二次函数的对称轴，再根据二次函数的增减性判断即可【解答】解：对称轴为直线 x 1，a20，x1 时，y 随 x 的增大而减小，x1 时，y 随 x 的增大而
18、增大，点 A（2，y 1）的对称点为（0，y 1），y 1y 2y 3故选：A【点评】本题考查了二次函数图象上点的坐标特征，求出对称轴解析式，然后利用二次函数的增减性求解更简便6（2 分）若一个扇形的半径是 18cm，面积是 54cm2，则扇形的圆心角为（ ）A30 B60 C90 D120【分析】设扇形的圆心角为 n，根据扇形面积公式计算即可【解答】解：设扇形的圆心角为 n，则 54 ，解得，n60，故选：B【点评】本题考查的是扇形面积计算，掌握扇形面积公式：S 是解题的关键7（2 分）如图，AB 是O 的切线，B 为切点，AO 的延长线交O 于 C 点，连接 BC，若A 30，AB 2 ，
19、则 AC 等于（ ）A4 B6 C D【分析】连接 OB，则AOB 是直角三角形，利用三角函数即可求得 OA 的长，则 AC即可求解【解答】解：连接 OBAB 是O 的切线，B 为切点，OBAB，在直角OAB 中，OB ABtanA2 2，则 OA2OB 4，AC4+26 故选：B【点评】本题考查了三角函数以及切线的性质，正确判断OAB 是直角三角形是关键8（2 分）二次函数 yax 2+bx+c（a，b，c 为常数，且 a0）中的 x 与 y 的部分对应值如表：x 1 0 1 3 y 1 3 5 3 下列结论：（1）ac0；（2）当 x1 时，y 的值随 x 值的增大而减小（3）3 是方程a
20、x2+（b1）x +c0 的一个根；（4）当1x 3 时，ax 2+（b1）x+c0其中正确的个数为（ ）A1 个 B2 个 C3 个 D4 个【分析】根据表格数据求出二次函数的对称轴为直线 x1.5，然后根据二次函数的性质对各小题分析判断即可得解【解答】解：（1）由图表中数据可得出：x1 时，y5，所以二次函数 yax 2+bx+c开口向下，a0；又 x0 时，y3，所以 c30，所以 ac0，故（1）正确；（2）二次函数 yax 2+bx+c 开口向下，且对称轴为 x 1.5，当 x1.5 时，y 的值随x 值的增大而减小，故（2）错误；（3）x3 时，y 3，9a+3b+c3，c 3，9
21、a+3b+33，9a+3b0，3 是方程 ax2+（b1）x +c0 的一个根，故（3）正确；（4）x1 时，ax 2+bx+c1，x1 时，ax 2+（b1）x +c0，x3 时，ax2+（b1）x +c0，且函数有最大值，当1x 3 时，ax 2+（b1）x+c0，故（4）正确故选：C【点评】本题考查了二次函数的性质，二次函数图象与系数的关系，抛物线与 x 轴的交点，二次函数与不等式，有一定难度熟练掌握二次函数图象的性质是解题的关键二、填空题（每小题 2 分，共 16 分）9（2 分）若二次函数 yx 2+2x+2k4 的图象与 x 轴有两个交点，则 k 的取值范围为 k 【分析】根据抛物
22、线与 x 轴有两个交点，求出的取值范围，即可求出 k 的取值范围【解答】解：根据题意知，2 241（2k4）0，解得：k ；故答案为：k 【点评】此题主要考查了抛物线与 x 轴交点问题解题的关键是熟练掌握二次函数的图象与性质10（2 分）如图，在平行四边形 ABCD 中，E 为 CD 上一点，连接 AE、BD，且 AE、BD交于点 F，S DEF ：S ABF 4：25，则 DE：EC 2：3 【分析】先根据平行四边形的性质及相似三角形的判定定理得出DEFBAF，再根据 SDEF ：S ABF4：10：25 即可得出其相似比，由相似三角形的性质即可求出 的值，由 ABCD 即可得出结论【解答】
23、解：四边形 ABCD 是平行四边形，ABCD，EAB DEF，AFBDFE，DEFBAF，S DEF ：S ABF 4：25， ，ABCD，DE：EC2：3故答案为：2：3【点评】本题考查的是相似三角形的判定与性质及平行四边形的性质，熟知相似三角形边长的比等于相似比，面积的比等于相似比的平方是解答此题的关键11（2 分）请写出一个开口向下，且经过点（1，0）的二次函数的解析式 yx 2+1（答案不唯一） 【分析】根据二次函数开口向下，所写出的二次函数 a0 即可【解答】解：二次函数 yx 2+1 开口向下，且经过（1，0）故答案为：yx 2+1（答案不唯一）【点评】本题考查了二次函数的性质，主
24、要利用了二次函数图象开口方向和二次函数图象上点的坐标特征，开放型题目，答案不唯一12（2 分）如图，PA，PB 是 O 的两条切线，切点分别为 A，B连接OA，OB，AB，PO，PO 与 AB 交于点 C若APB60，OC1，则PAB 的周长为 6 【分析】根据切线的性质得到 OAPA，OB PB ，OP 平分APB，PAPB，推出PAB 是等边三角形，根据直角三角形的性质求出 AC，由 AB2AC ，于是得到结论【解答】解：PA、PB 是O 的两条切线，OAPA，OBPB，OP 平分APB，PAPB，APB 60，PAB 是等边三角形，AB2AC，PO AB，PAB 60，OACPAOPAB
25、906030，AO2OC，OC1，AO2，AC ，AB2AC2 ，PAB 的周长6 故答案为：6 【点评】本题考查了切线的性质，直角三角形的性质，三角形的周长的计算，熟练掌握切线的性质是解题的关键13（2 分）如图，四边形 ABCD 是O 内接四边形，若 BAC30，CBD80，则BCD 的度数为 70 【分析】先根据圆周角定理求出BAD 的度数，再由圆内接四边形的性质即可得出结论【解答】解：CBD80，CADCBD80BAC30，BAD30+80110四边形 ABCD 是O 内接四边形，BCD180BAD18011070故答案为：70【点评】本题考查的是圆内接四边形的性质，熟知圆内接四边形的
26、对角互补是解答此题的关键14（2 分）如图是一个隧道的横截图，它的形状是以点 O 为圆心的一部分，如果 M 是O 中弦 CD 的中点，EM 经过圆心 O 交O 于点 E，若 CD4m，EM 6m，则O 的半径为 m【分析】因为 M 是O 弦 CD 的中点，根据垂径定理，EMCD，则 CMDM2，在RtCOM 中，有 OC2CM 2+OM2，进而可求得半径 OC【解答】解：M 是O 弦 CD 的中点，根据垂径定理：EMCD，又 CD4 则有：CM CD2，设圆的半径是 x 米，在 Rt COM 中，有 OC2CM 2+OM2，即：x 22 2+（6x ） 2，解得：x ，所以圆的半径长是 故答案
27、为： 【点评】此题主要考查了垂径定理的应用，解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为 r，弦长为 a，这条弦的弦心距为 d，则有等式 r2d 2+（ ） 2 成立，知道这三个量中的任意两个，就可以求出另外一个15（2 分）已知在 RtABC 中，C90，AC6，BC3我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”（1）如图 1，四边形 CDEF 是ABC 的内接正方形，则正方形 CDEF 的边长 a1 等于 2 ；（2）如图 2，四边形 DGHI 是（1）中EDA 的内接正方形，那么第 2 个正方形 DGHI的边长记为 a2
28、；继续在图 2 中的HGA 中按上述方法作第 3 个内接正方形，依此类推，则第 n 个内接正方形的边长 an （n 为正整数）【分析】（1）由正方形的性质可以得出BFEBCA ，再根据相似三角形的性质就可以把正方形 CDEF 的边长表示出来，从而得出结论（2）由正方形的性质可以得出EIHEDA，再根据相似三角形的性质就可以把正方形 IDGF 的边长表示出来，从而得出结论，通过计算得出的结论寻找其中的变化规律就可以得出第 n 个内接正方形的边长的值【解答】解：（1）四边形 CDEF 是正方形，EFFC，EFFC，BFE BCA， ， ，a 12，故答案是：2；（2）如图（2）四边形 DGHI 是
29、正方形，IH ID，IHAD，EIHEDA， ， ，a 2 ，如图 3 中，由以上同样的方法可以求得正方形 PGQS 的边长为： ，第 4 的个正方形的边长为： ，第 n 个内接正方形的边长 an ，故答案为： 【点评】本题考查了正方形的性质的运用，相似三角形的判定与性质，勾股定理的运用及规律的探索16（2 分）如图，RtABC 中，ABBC ，AB6，BC4，P 是ABC 内部的一个动点，且满足PABPBC，则线段 CP 长的最小值为 2 【分析】首先证明点 P 在以 AB 为直径的 O 上，连接 OC 与O 交于点 P，此时 PC最小，利用勾股定理求出 OC 即可解决问题【解答】解：ABC
30、90，ABP +PBC 90，PAB PBCBAP +ABP90，APB 90，点 P 在以 AB 为直径的 O 上，连接 OC 交O 于点 P，此时 PC 最小，在 RTBCO 中，OBC 90，BC 4，OB 3，OC 5，PCOCOP532 PC 最小值为 2 故答案为 2【点评】本题考查点与圆位置关系、圆周角定理、最短问题等知识，解题的关键是确定点 P 位置，学会求圆外一点到圆的最小、最大距离，属于中考常考题型三、解答题17（5 分）在数学课上，老师提出利用尺规作图完成下面问题：已知：ABC 是O 的内接三角形求作：ABC 中BAC 的平分线小明的作法如下：（1）作 BC 边的垂直平分
31、线 DE，交 BC 于点 D，交弧 BC 于点 E；（2）连接 AE，交 BC 边于点 F；则线段 AF 为所求ABC 中BAC 的平分线根据小明设计的尺规作图过程，（1）在图中补全图形（尺规作图，保留作图痕迹）；（2）完成下面的证明证明：OBOC，DE 是线段 BC 的垂直平分线圆心 O 在直线 DE 上（ 到线段两端点距离相等的点在线段的垂直平分线上 ）DEBC， （ 垂径定理 ）BAE CAE（ 圆周角定理 ），线段 AF 为所求ABC 中BAC 的平分线【分析】（1）根据几何语言画出对应的几何图形；（2）根据线段垂直平分线的性质得到 DEBC，则利用垂径定理得到弧 BE弧 CE，然后根
32、据圆周角定理得到BAECAE 【解答】解：（1）如图，（2）证明：OBOC，DE 是线段 BC 的垂直平分线圆心 O 在直线 DE 上（到线段两端点距离相等的点在线段的垂直平分线上）DEBC， （垂径定理）BAE CAE（圆周角定理），线段 AF 为所求ABC 中BAC 的平分线故答案为到线段两端点距离相等的点在线段的垂直平分线上；垂径定理；圆周角定理【点评】本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作也考查了垂径定理和圆周角定理18
33、（5 分）计算：tan60sin 245+tan452cos30【分析】直接利用特殊角的三角函数值代入求出答案【解答】解：原式 （ ） 2+12 +1 【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键19（5 分）如图，四边形 ABCD 各顶点的坐标分别为 A（2，6），B（4，2），C（6，2），D（6，4）（1）在第一象限内，以原点 O 为位似中心，画出四边形 ABCD 的位似图形 A1B1C1D1，使对应边长变为原来的 ；（2）将线段 AB 绕点 B 顺时针旋转 90得到线段 A2B，画出线段 A2B，并计算点 A 所经过的路径长【分析】（1）根据位似变换的定义作出变
34、换后的对应点，再顺次连接即可得；（2）根据旋转的定义和弧长公式计算可得【解答】解：（1）如图所示，四边形 A1B1C1D1 即为所求（2）如图所示，线段 A2B 即为所求，A 2B 2 ，ABA 290，点 A 所经过的路径长为 【点评】本题主要考查作图位似变换和旋转变换，解题的关键是掌握位似变换和旋转变换的定义和性质，并据此得出变换后的对应点20（5 分）已知抛物线 yx 24x +2（1）此抛物线与 y 轴的交点坐标是 （0，2） ，顶点坐标是 （2，2） ；（2）在坐标系中利用描点法画出此抛物线；x y （3）结合图象回答：垂直于 y 轴的直线 l 与抛物线 yx 24x+2 相交于点
35、P（x 1，y 1），Q（x 2，y 2），则x1+x2 4 ；若点 A（5， t）和点 B（m，n）都在抛物线 yx 24x+2 上，且 nt，则 m 的取值范围是 1m5 【分析】（1）利用待定系数法配方法即可解决问题；（2）利用描点法即可解决问题；（3） 根据题意即可求得；根据二次函数的性质以及对称性即可求得【解答】解：（1）对于抛物线 yx 24x +2 令 x0 得到 y2，与 y 轴交点的坐标为（0，2）；yx 24x+2（x2） 22，顶点坐标（2，2），故答案为：（0，2），（2，2）；（2）利用描点法画出图象如图所示：x 0 1 2 3 4 y 2 1 2 1 2 （3）结合
36、图象：垂直于 y 轴的直线 l 与抛物线 yx 24x+2 相交于点 P（x 1，y 1），Q（x 2，y 2），则x1+x24；若点 A（5， t）和点 B（m，n）都在抛物线 yx 24x+2 上，且 nt，则 m 的取值范围是1m5；故答案为 4；1m5【点评】本题考查抛物线与 x 轴的交点、二次函数的性质等知识，解题的关键是熟练掌握二次函数的性质21（6 分）如图，在矩形 ABCD 中，AB2，BC4，对角线 AC 与 BD 交于点 O，点 E在 BC 边上，DE 与 AC 交于点 F，CDECBD求：（1）CE 的长；（2）EF 的长【分析】（1）由在矩形 ABCD 中，EDCADB
37、，易证得CDECBD，然后由相似三角形的对应边成比例，求得答案；（2）首先求得CDE 的面积，然后证得ADFCEF，即可得：EF：DE1：5，根据勾股定理得到 DE，于是得到结论【解答】解：（1）四边形 ABCD 是矩形，AB2，BC4，ADBC，CDAB2，ADBCBD，EDCADB，EDCCBD，ECDDCB，CDECBD，CE：CDCD：CB，CE：22：4，解得：CE1；（2）ADBC，ADFCEF，DF：EFAD：CE4：1，EF：DE 1：5，DCB90，DE ，EF 【点评】此题考查了相似三角形的判定与性质以及矩形的性质注意证得CDECBD 与ADFCEF 是关键22（5 分）已
38、知：如图，斜坡 AP 的坡度为 1：2.4，坡长 AP 为 26 米，在坡顶 A 处的同一水平面上有一座古塔 BC，在斜坡底 P 处测得该塔的塔顶 B 的仰角为 45，在坡顶 A处测得该塔的塔顶 B 的仰角为 76求：（1）坡顶 A 到地面 PQ 的距离；（2）古塔 BC 的高度（结果精确到 1 米）（参考数据：sin76 0.97，cos76 0.24，tan764.01）【分析】（1）过点 A 作 AHPQ ，垂足为点 H，利用斜坡 AP 的坡度为 1：2.4，得出AH，PH，AP 的关系求出即可；（2）利用矩形性质求出设 BCx ，则 x+1024+DH，再利用 tan76 ，求出即可【
39、解答】解：（1）过点 A 作 AHPQ ，垂足为点 H斜坡 AP 的坡度为 1：2.4， ，设 AH5km，则 PH12km ，由勾股定理，得 AP13km13k26m 解得 k2AH10m答：坡顶 A 到地面 PQ 的距离为 10m（2）延长 BC 交 PQ 于点 DBCAC，ACPQ，BDPQ 四边形 AHDC 是矩形，CDAH10，AC DHBPD45，PDBD 设 BCx，则 x+1024+ DHACDHx14在 Rt ABC 中，tan76 ，即 4.0，解得 x ，即 x19，答：古塔 BC 的高度约为 19 米【点评】此题主要考查了坡度问题以及仰角的应用，根据已知在直角三角形中得
40、出各边长度是解题关键23（5 分）如图，在ABC 中，ACB 90，CD 为 AB 边上的中线，过点 D 作DEBC 于 E，过点 C 作 AB 的平行线与 DE 的延长线交于点 F，连接 BF（1）求证：四边形 BDCF 为菱形；（2）若 CE4，AC6，求四边形 BDCF 的面积【分析】（1）求出四边形 ADFC 是平行四边形，推出 CFADBD，根据平行四边形的判定得出四边形 BDCF 是平行四边形，求 CDBD，根据菱形的判定得出即可；（2）由菱形的性质和平行四边形的性质可得 DFAC6，BC8，即可求四边形BDCF 的面积【解答】证明：（1）DE BC，ACB90，BEDACB，DF
41、AC，CFAB，四边形 ADFC 是平行四边形，ADCF，D 为 AB 的中点，ADBD ，BDCF，BDCF，四边形 BDCF 是平行四边形，ACB90，D 为 AB 的中点，DCBD，四边形 BDCF 是菱形；（2）四边形 BDCF 是菱形BC2CE8，BCDF四边形 ADFC 是平行四边形，DFAC6S 菱形 BDCF BCDF24【点评】本题考查了菱形的性质和判定，平行四边形的性质和判定，直角三角形的性质，熟练运用这些性质进行推理是本题的关键24（6 分）如图，在ABC 中，ABAC ，以 AB 为直径的O 分别交 AC，BC 于点D，E，过点 B 作O 的切线，交 AC 的延长线于点
42、 F（1）求证：CBF CAB；（2）连接 BD，AE 交于点 H，若 AB5，tanCBF ，求 BH 的值【分析】（1）连接 AE，利用等腰三角形的性质易证BAECAE CAB，由弦切角定理可得CBDBAE，所以CBF CAB（2）由 tanCBFtanEAB ，得出 ，根据勾股定理求得 BE，根据圆周角定理得出BAECAE，即可得出 EBD EAB ，由 EBDEAB，得出tanEBD ，即可求得 EH，然后根据勾股定理求得 BH 即可【解答】（1）证明：连接 AE，AB 是圆的直径，AEBC，ABAC，AE 平分BAC，BAE CAE CAB，BF 是O 的切线，CBFBAE，CBF
43、CAB（2）解：tanCBF tanEAB ， ，AB5，AB 2BE 2+AE2，25BE 2+4BE2，BE ，BAE CAE，EBD CAE ，EBDEAB，tanEBD ，EH ，BH 【点评】本题考查了弦切角定理的运用、圆周角定理，勾股定理，直角三角函数以及等腰三角形的性质，解题的关键是正确的添加辅助线，利用等腰三角形的性质解题25（6 分）如图，半圆 O 的直径 AB5cm ，点 M 在 AB 上且 AM1cm ，点 P 是半圆 O上的动点，过点 B 作 BQPM 交 PM（或 PM 的延长线）于点 Q设PMxcm，BQycm（当点 P 与点 A 或点 B 重合时，y 的值为 0）
44、小石根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：x/cm 1 1.5 2 2.5 3 3.5 4y/cm 0 3.7 4 3.8 3.3 2.5 0 （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当 BQ 与直径 AB 所夹的锐角为 60时，PM 的长度约为 1.1 或 3.7 cm【分析】（1）当 x2 时，PMAB ，此时 Q 与 M 重合，BQBM4，当 x4 时，点P 与 B 重合，此时 BQ0（2）利用描点法画出函数图象即可；（3）根据直角三角形 30 度角的性质，求出 y2，观察图象写出对应的 x 的值即可；【解答】解：（1）当 x2 时，PMAB ，此时 Q 与 M 重合，BQBM4，当 x4 时，点 P 与 B 重合，此时 BQ0故答案为 4，0（2）函数图象如图所示：
