1、第 1 页，共 18 页2019 年广东省汕头市潮阳一中等七校联合体高考数学冲刺试卷（文科） （5 月份）一、选择题（本大题共 12 小题，共 60.0 分）1. 设集合 M=x|0x1，N=x|x|1，则 MN=（ ）A. B. 或|01 |1 0C. 或 D. |1 01 12. 若复数 z= ，则 =（ ）11+ A. 1 B. C. i D. 1 3. 甲乙两名同学 6 次考试的成绩统计如图，甲乙两组数据的平均数分别为 、 标甲 乙准差分别为 甲 、 乙 ，则（ ）A. ， B. ，甲 乙C. ， D. ，甲 乙 甲 乙 甲 乙4. 已知数列a n为等差数列，且 a5=5，则 S9 的
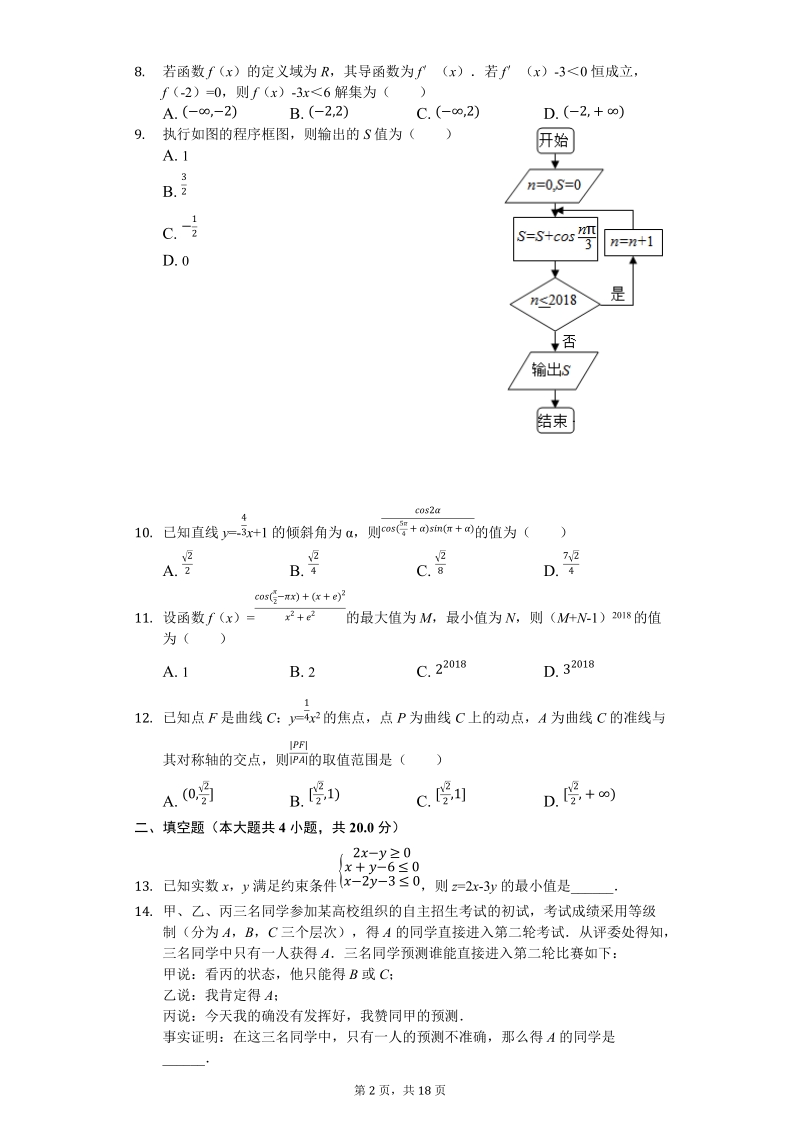
2、值为（ ）A. 25 B. 45 C. 50 D. 905. 已知 a=（ ） ，b= （ ） ，c=log 3，则 a，b，c 的大小关系为（ ）13 23 14 13A. B. C. D. 6. 一只蚂蚁在边长为 4 的正三角形区域内随机爬行，则它在离三个顶点距离都大于2 的区域内的概率为（ ）A. B. C. D. 136 34 36 147. 已知某几何体的三视图如图所示，则该几何体的最大边长为（ ）A. B. C. D. 5 6 7 22第 2 页，共 18 页8. 若函数 f（x ）的定义域为 R，其导函数为 f（x ）若 f（x）-30 恒成立，f（-2）=0，则 f（x ）-3
3、x6 解集为（ ）A. B. C. D. (,2) (2,2) (,2) (2,+)9. 执行如图的程序框图，则输出的 S 值为（ ）A. 1B. 32C. 12D. 010. 已知直线 y=- x+1 的倾斜角为 ，则 的值为（ ）43 2(54+)(+)A. B. C. D. 22 24 28 72411. 设函数 f（x ）= 的最大值为 M，最小值为 N，则（M +N-1） 2018 的值(2)+(+)22+2为（ ）A. 1 B. 2 C. D. 22018 3201812. 已知点 F 是曲线 C：y = x2 的焦点，点 P 为曲线 C 上的动点，A 为曲线 C 的准线与14其对
4、称轴的交点，则 的取值范围是（ ）|A. B. C. D. (0,22 22,1) 22,1 22,+)二、填空题（本大题共 4 小题，共 20.0 分）13. 已知实数 x，y 满足约束条件 ，则 z=2x-3y 的最小值是_20+6023014. 甲、乙、丙三名同学参加某高校组织的自主招生考试的初试，考试成绩采用等级制（分为 A，B，C 三个层次），得 A 的同学直接进入第二轮考试从评委处得知，三名同学中只有一人获得 A三名同学预测谁能直接进入第二轮比赛如下：甲说：看丙的状态，他只能得 B 或 C；乙说：我肯定得 A；丙说：今天我的确没有发挥好，我赞同甲的预测事实证明：在这三名同学中，只有
5、一人的预测不准确，那么得 A 的同学是_第 3 页，共 18 页15. 在ABC 中，内角 A，B，C 所对的边分别为 a，b，c，已知（a+b- c）（a+b+c）=3ab，且 c=4，则ABC 面积的最大值为_16. 在平面上， ，且 | |=2，| |=1， = + 若| |=| |，则| |的取值1 2 1 2 1 2 1 2 范围是_三、解答题（本大题共 7 小题，共 82.0 分）17. 已知数列a n的前 n 项和为 Sn，且满足 Sn= （a n-1），nN *43（）求数列a n的通项公式；（）令 bn=log2an，记数列 的前 n 项和为 Tn证明：T n 1(1)(+1
6、) 1218. 据统计，2017 年国庆中秋假日期间，黔东南州共接待游客 590.23 万人次，实现旅游收入 48.67 亿元，同比分别增长 44.57%、55.22% 旅游公司规定：若公司导游接待旅客，旅游年总收入不低于 40（单位：百万元），则称为优秀导游经验表明，如果公司的优秀导游率越高，则该公司的影响度越高已知甲、乙两家旅游公司各有导游 100 名，统计他们一年内旅游总收入，分别得到甲公司的频率分布直方图和乙公司的频数分布表如下：分组 10，20） 20，30） 30，40） 40，50） 50，60）频数 b 18 49 24 5（）求 a，b 的值，并比较甲、乙两家旅游公司，哪家的
7、影响度高？（）若导游的奖金 y（单位：万元），与其一年内旅游总收入 x（单位：百万元）之间的关系为 y= ，求甲公司导游的年平均奖金；1， 202， 20 403， 40（）从甲、乙两家公司旅游收入在50，60）的总人数中，用分层抽样的方法随机抽取 6 人进行表彰，其中有两名导游代表旅游行业去参加座谈，求参加座谈的导游中有乙公司导游的概率第 4 页，共 18 页19. 在四棱锥 P-ABCD 中，四边形 ABCD 是矩形，平面PAB平面 ABCD，点 E、F 分别为 BC、AP 中点（1）求证：EF 平面 PCD；（2）若 AD=AP=PB= AB=1，求三棱锥 P-DEF 的体22积20.
8、已知点 A（0，-1）、B （0，1），P 为椭圆 C： +y2=1 上异于点 A，B 的任意一22点（）求证：直线 PA、PB 的斜率之积为- ；12（）是否存在过点 Q（-2，0）的直线 l 与椭圆 C 交于不同的两点 M、N，使得|BM|=|BN|？若存在，求出直线 l 的方程；若不存在，请说明理由21. 已知函数 f（x ）=x 2+1，g（x）=2aln x+1（a R）（1）求函数 h（x）=f（x）- g（x ）的极值；（2）当 a=e 时，是否存在实数 k，m ，使得不等式 g（x ）kx+mf（x）恒成立？若存在，请求实数 k，m 的值；若不存在，请说明理由第 5 页，共 1
9、8 页22. 在平面直角坐标系 xOy 中，将曲线 C1： （ 为参数）上任意一点=P（x ， y）经过伸缩变换 后得到曲线 C2 的图形以坐标原点 O 为极点，=3=2x 轴的非负半轴为极轴，取相同的单位长度建立极坐标系，已知直线 l：（2cos-sin）=8（）求曲线 C2 和直线 l 的普通方程；（）点 P 为曲线 C2 上的任意一点，求点 P 到直线 l 的距离的最大值及取得最大值时点 P 的坐标23. 已知函数 f（x ）=|3 x-1|+|3x+k|，g（x ）= x+4（）当 k=-3 时，求不等式 f（x）4 的解集；（）设 k-1 ，且当 x- ， ）时，都有 f（x）g（x
10、），求 k 的取值范围3 13第 6 页，共 18 页答案和解析1.【答案】D【解析】解：N=x|x-1，或 x1； MN=1 故选：D可求出 N，然后进行交集的运算即可考查绝对值不等式的解法，描述法、列举法表示集合的概念，以及交集的运算2.【答案】C【解析】解：z= = ， 故选：C 利用复数代数形式的乘除运算化简，再由共轭复数的概念得答案本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础的计算题3.【答案】C【解析】解：甲乙两名同学 6 次考试的成绩统计如图，甲乙两组数据的平均数分别为 、标准差分别为 甲 、 乙 ，由折线图得： ， 甲 乙 ，故选：C 利用折线图的性质直接求解第
11、7 页，共 18 页本题考查命题真假的判断，考查折线图等基础知识，考查运算求解能力、数据处理能力，考查函数与方程思想、数形结合思想，是基础题4.【答案】B【解析】解：数列a n为等差数列，且 a5=5，则 S9= = =9a5=45，故选：B 根据等差数列的性质和求和公式即可求出本题考查了等差数列的性质和求和公式，属于基础题5.【答案】D【解析】解：0 a=（ ） （ ）0=1，（ ） b= （ ） =（ ） （ ）0=1，c=log3log 33=1，a，b，c 的大小关系为 cba故选：D利用指数函数、对数函数的单调性直接求解本题考查三个数的大小的比较，考查指数函数、 对数函数的单调性等基
12、础知识，考查运算求解能力，考查函数与方程思想，是基础题6.【答案】A【解析】解：满足条件的正三角形 ABC 如下图所示：其中正三角形 ABC 的面积 S 三角形= 16=4 ，满足到正三角形 ABC 的顶 点 A、B、C的距离至少有一个小于 2 的平面区域如图中阴影部分所示，则 S 阴影 =2，则使取到的点到三个顶点 A、B、C 的距离都大于 2 的概率是：第 8 页，共 18 页P=1- =1- ，故选：A求出满足条件的正三角形 ABC 的面积，再求出满足条件正三角形 ABC 内的点到正方形的顶点 A、B、C 的距离均不小于 2 的图形的面积，然后代入几何概型公式即可得到答案本题考查几何概型
13、概率公式、三角形的面积公式、扇形的面积公式几何概型的概率估算公式中的“ 几何度量 ”，可以 为线段长度、面积、体积等，而且 这个“几何度量 ”只与“大小”有关，而与形状和位置无关7.【答案】B【解析】解：由三视图还原原几何体如图，可知该几何体为四棱锥，底面 ABCD 为直角梯形，ADCD，PA底面 ABCD，PA=AD=AB=1，CD=2由图求得PD= ，BC= ，PB= ，PC= 则该几何体的最大边长为 故选：B 由三视图还原原几何体，可知该几何体为四棱锥，底面 ABCD 为直角梯形，ADCD，PA底面 ABCD，PA=AD=AB=1，CD=2求解三角形分别求出未知边长得答案本题考查由三视图
14、求面积、体积，关 键是由三视图还原原几何体，是中档 题8.【答案】D【解析】解：令 g（x）=f（x）-3x， 故 g（x）=f（x）-30， 故 g（x）在 R 递减， 而 g（-2）=f（-2）=6， 故 f（x）-3x 6， 即 g（x）g（-2）， 第 9 页，共 18 页故 x-2 ， 故选：D令 g（x）=f（x）-3x，求出函数的导数，根据函数的单调性求出不等式的解集即可本题考查了函数的单调性问题，考查导数的应用，是一道中档题9.【答案】D【解析】解：模拟程序的运行，可得程序运行后计算并输出 S=cos0+cos + +cos的值由于 S=cos0+cos +cos +cos=1
15、+（cos +cos +cos2）336+cos +cos +cos=1+0+ - -1=0故选：D根据程序框图，得出 n=20192018 时，输出 S利用三角函数的周期性即可得出本题考查了算法与程序框图、三角函数的周期性与求值，考查了推理能力与计算能力，属于基础题10.【答案】B【解析】解：由已知可得 tan= ， = = = = 故选：B 由已知求得 tan，再由两角和的余弦、二倍角余弦及诱导公式变形，最后化弦为切求解第 10 页，共 18 页本题考查三角函数中的恒等变换应用，考查三角函数的化简求值，是中档题11.【答案】A【解析】解：f（x ）= = = +1，设 g（x）= ，g（-
16、x）=-g（x），g（x）为 奇函数，g（x）max+g（x）min=0，M+N=g（x）max+g（x）min+2=2，（M+N-1）2018=1，故选：A化简 f（x）= +1，设 g（x）= ，根据奇函数的性质，即可求出 M+N=2，代值计算即可本题考查了函数解析式的变形及单调性与最值的关系，属于中档题12.【答案】C【解析】解：A（0， -1），准线方程为 y=-1，过 P 作准线的垂线 PM，则 PM=PF，显然当 P 与 O 重合时， =1，当 P 与 O 不重合时， =sinPAM，故而当 AP 与抛物线相切时， PAM 取得最小值，不妨设 P 在第一象限， P（x0， ），则直
17、线 AP 的斜率为 ，又 A（0，-1）在直线 AP 上， = ，解得 x0=2故而直线 AP 的斜率为 1，即 PAM 的最小值为 45，第 11 页，共 18 页 的最小值为 sin45= 故选：C 分 P 是否为原点 讨论计算，根据抛物线的定义和切线的性质计算本题考查了抛物线的性质，切线的求解计算，属于中档题13.【答案】-8【解析】解：实数 x，y 满足约束条件的可行域如图：目标函数 z=2x-3y，点 A（2，4），z 在点 A 处有最小 值：z=22-34=-8，故答案为：-8 先根据约束条件画出可行域，再利用几何意义求最值，z=2x-3y 表示直线在 y轴上的截距，只需求出可行域
18、直线在 y 轴上的截距最值即可本题主要考查了简单的线性规划，将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解，是常用的一种方法14.【答案】甲【解析】解：若得 A 是甲，则甲预测 准确，乙预测不正确，丙预测准确，满足条件 若得 A 是乙，则甲预测准确，乙预测正确，丙预测准确，不满足条件 若得 A 是丙，则甲预测不准确，乙预测不正确，丙预测不准确，不满足条件 故满足条件的是甲，即得 A 的同学是甲， 故答案为：甲根据条件分别判断得 A 的同学是甲乙丙，然后 进行判断即可本题主要考查合情推理的应用，根据条件进行假设是解决本题的关键15.【答案】 43【解析】第 12 页，共 18 页
19、解：在ABC 中，内角 A，B，C 所对的边分别为 a，b，c，已知（a+b-c）（a+b+c ）=3ab，则：a 2+b2-c2=ab，整理得：cosC= = ，由于：0C ，解得：C= 由于：c=4，故：c 2=a2+b2-2abcosC，转换为：162ab-ab=ab，所以： 故最大值为：4 首先利用关系式的变换，转换为余弦定理的关系式，求出 C 的值， 进一步利用余弦定理和基本关系式求出 ab 的最大值，最后利用三角形的面积公式求出结果本题考查的知识要点：余弦定理和三角形面积公式的应用，基本不等式的应用16.【答案】 ，+ ）3510【解析】解：以 O 为原点，以 OB2，OB1 所在
20、直线为坐标轴建立平面直角坐标系，则 B1（0，2），B2（1，0），P=（1，2），| |=| |，M 点的 轨迹为为线段B1B2 的中垂线 l，直线 l 的方程为 y= （x- ）+1，即 x-2y+ =0，P 到直线 l 的距离为 d= = | | 第 13 页，共 18 页故答案为：建立坐标系，求出 M 的轨迹所在直线方程和 P 点坐标，从而得出答案本题考查了平面向量的数量积运算，属于中档题17.【答案】（I）解：当 n=1 时，有 ，解得 a1=41=1=43(11)当 n2 时，有 Sn-1= （a n-1-1），43则 ，=1=43(1)43(11)整理得：a n=4an-1，数列
21、 an是以 q=4 为公比，以 4 为首项的等比数列=441=4()即数列a n的通项公式为： =4()（II）证明：由（I）有 ，则=2=24=2，1(+1)(1)= 1(2+1)(21)=12( 12112+1)Tn= + = ，12(113)+(1315) ( 12112+1) 12(112+1) 12故得证【解析】（I）当 n=1 时，有 ，解得 a1当 n2时，有 Sn-1= （an-1-1），可得 ，利用等比数列的通项公式即可得出（ II）由（I）有 ，则，利用裂项求和方法可得 Tn，即可证 明本题考查了数列递推关系、等比数列的通项公式、裂项求和方法、数列的 单调性，考查了推理能力
22、与计算能力，属于中档 题18.【答案】（12 分）解：（I）由直方图知：（0.01+0.025+0.035+a+0.01 ）10=1，解得 a=0.02，由频数分布表知：b+18+49+24+5=100，解得 b=4甲公司的导游优秀率为：（0.02+0.01）10100%=30%；第 14 页，共 18 页乙公司的导游优秀率为： ；24+5100100%=29%由于 30%29%，所以甲公司的影响度高 （4 分）（II）甲公司年旅游总收入10 ，20）的人数为 0.0110100=10 人，年旅游总收入20，40）的人数为（ 0.025+0.035）10100=60 人，年旅游总收入40，60
23、）的人数为（ 0.02+0.01）10100=30 人，故甲公司导游的年平均奖金 （万元） （8 分）=110+602+303100 =2.2（III）由已知得，年旅游总收入在50，60）的人数为 15 人，其中甲公司 10 人，乙公司 5 人按分层抽样的方法甲公司抽取 6 =4 人，记为 a，b，c， d，1015从乙公司抽取 6 =2 人，记为 1，2则 6 人中随机抽取 2 人的基本事件有：515（a，b），（a，c），（a，d），（a，1），（a，2），（b，c），（b，d），（b，1），（b，2），（c，d），（c，1），（c ，2），（ d，1），（d，2），（1，2）共 15 个
24、参加座谈的导游中有乙公司导游的基本事件有：（a，1），（a，2），（b，1），（b，2），（c，1），（c，2），（d，1），（d，2），（1，2）共 9 个设事件 A 为“参加座谈的导游中有乙公司导游”，则 P（A）= = ，所求概率为 （12 分）91535 35【解析】（I）由频 率分布直方图能求出 a，由频数分布表求出 b=4由此求出甲公司的导游优秀率和乙公司的导游优秀率，从而得到甲公司的影响度高 （ II）甲公司年旅游 总收入10，20）的人数为 10 人，年旅游总收入20，40）的人数为 60 人，年旅游总收入40， 60）的人数为 30 人，由此能求出甲公司导游的年平均奖金 （
25、III）年旅游总收入在50， 60）的人数为 15 人，其中甲公司 10 人，乙公司 5人按分层抽样的方法甲公司抽取 4 人， 记为 a，b，c，d，从乙公司抽取 2 人，记为 1，2从 6 人中随机抽取 2 人，利用列 举法能坟 出参加座谈的导游中有乙公司导游的概率本题考查实数值的求法，考查频率分布直方图的应用，考查概率的求法等基础知识，考查运算求解能力，考查函数与方程思想，是基础题第 15 页，共 18 页19.【答案】（1）证明：取 PD 中点 G，连接 GF，GC在PAD 中，有G，F 分别为 PD、AP 中点，/ 12在矩形 ABCD 中，E 为 BC 中点， ， ，/ 12 / 四
26、边形 ABCD 是平行四边形，GCEFGC平面 PCD，EF平面 PCD，EF平面 PCD解：（2）四边形 ABCD 是矩形，AD AB，ADBC ，平面 PAB平面 ABCD，平面 PAB平面 ABCD=AB，AD平面 PAB，AD平面 PAB，平面 PAD平面 PAB，BC平面 PAD， ， ，满足 AP2+PB2=AB2，=22=1 =2APPB， BP平面 PAD，BC平面 PAD，点 E 到平面 PAD 的距离等于点 B 到平面 PAD 的距离 ，=12=12121=14 ，=13=13141=112三棱锥 P-DEF 的体积为 112【解析】（1）取 PD 中点 G，连接 GF，G
27、C推 导出四边形 ABCD 是平行四边形，从而GCEF，由此能证明 EF平面 PCD （2）推导出 ADAB，ADBC，从而 AD平面 PAB，进而平面 PAD平面PAB，BC平面 PAD，推导出 APPB，从而 BP平面 PAD，由 BC平面PAD，得点 E 到平面 PAD 的距离等于点 B 到平面 PAD 的距离，由此能求出三棱锥 P-DEF 的体积本题考查线面平行的证明，考查三棱锥的体积的求法，考查空间中线线、 线面、面面间的位置关系等基础知识，考 查推理论证能力、空间想象能力、运算求解能力，考查函数与方程思想、数形结合思想，是中档题20.【答案】解：（I）证明：设点 P（x，y），（x
28、0），则 +y2=1，22即 ，2=122第 16 页，共 18 页 =1+1 212= = ，故得证(122)12 12（II）假设存在直线 l 满足题意显然当直线斜率不存在时，直线与椭圆 C 不相交当直线 l 的斜率 k0 时，设直线 l 为：y=k （x+2），联立椭圆方程 x2+2y2=2，化简得（1+2k 2）x 2+8k2x+8k2-2=0，由=64k 4-4（1+2k 2）（8k 2-2）0，解得 ，22 22(0)设点 M（x 1，y 1），N（x 2，y 2），则 ，1+2=821+2212=8221+22y1+y2=k（x 1+x2）+4 k=k +4k= ，821+22
29、41+22取 MN 的中点 H，即 ，(1+22， 1+22 )则 k=-1，1+2211+22即 ，21+221421+22=1化简得 2k2+2k+1=0，无实数解，故舍去当 k=0 时，M，N 为椭圆 C 的左右顶点，显然满足| BM|=|BN|，此时直线 l 的方程为 y=0综上可知，存在直线 l 满足题意，此时直线 l 的方程为 y=0【解析】（I）设点 P（x，y），（x0），代入椭圆方程，由直 线的斜率公式，即可得证； （II）假设存在直 线 l 满足题 意显然当直线斜率不存在 时，直线与椭圆 C 不相交，讨论直线的斜率是否为 0，联立直线方程和椭圆方程，运用 韦达定理和两直线垂
30、直的条件：斜率之积为-1，可得所求直线方程本题考查椭圆方程的运用，考查直线方程和椭圆方程联立，运用韦达定理和两直线垂直的条件：斜率之积为-1，考查运算能力和分类讨论思想方法，属于中档题第 17 页，共 18 页21.【答案】解：（1）h（x）=f （x）- g（x ）= x2-2alnx，x0，h（x）= ，2(2)当 a0，h（x ）0，则 h（x ）在（0，+ ）上单调递增，无极值，当 a0 时，h（x）0，即 x2-a0，解得：a 或 x- ，（舍去） h（x）0，即 x2-a0，解得：0x ，h（ x）在（0， ）单调递减，在（ ，+）单调递增， h（ x）的极小值为 h（ ）=a-2
31、 aln =a-alna，无极大值； （2）当 a=e 时，h（ ）= h（ ）=e-elne=0 ，此时 h（x ）=f（x）-g（x ）=0 ， f（x）- g（x）0，当且仅当 x= 时，取等号；f（x）=2x，f（ ）=2 ，g（x）= ，g（ ）=2 ， 2 f（ ）=g（ ）， 且在 x= 处 f（ ）= g（ ）= e+1， 即 x= 时，y=f（x）与 y=g（ x）有公切线，切线方程 y=2 x+1-e， 此时 g（x）=2 x+1-e=f（x ），满足 g（x ）kx+ mf（x ）恒成立，解得：k=2 ，m=1-e，实数 k，m 的值分别为 2 ，1-e【解析】（1）求导
32、，分类讨论，根据导数与函数单调性的关系，根据函数的单调性即可求得 h（x）极值；（2）当 a=e 时，由 f（x）-g（x）0，当且 仅当 x= 时，取等号，由 f（ ）=g（ ），则 x= 时，y=f（x）与 y=g（x）有公切线，切线方程 y=2 x+1-e，即可求得实数 k，m 的值本题考查导数的综合应用，考查利用导数的求函数的单调性及最值，考查利用导数求曲线的切线方程，考查计算能力，属于中档题22.【答案】解：（I）由已知有 （ 为参数），消去 得 =3=2 23+24=1将 代入直线 l 的方程得： 2x-y=8=曲线 C2 的方程为 ，23+24=1直线 l 的普通方程为：2x -
33、y=8（II）由（I）可设点 P 为（ ），0，2）3， 2则点 P 到直线 l 的距离为：d= ，|2328|5 =|4(3)+8|5则： ，=1255第 18 页，共 18 页点 P（ ）32， 1【解析】（）利用伸缩变换求出曲线的方程，进一步转换求出结果 （）利用三角函数的关系式的变换和点到直线的距离公式求出结果本题考查的知识要点：曲线的伸缩变换的应用，方程的转换，点到直线的距离公式的应用23.【答案】解：（I）当 k=-3 时，f（x ）= ，6+4， 132， 13164， 1故不等式 f（x） 4 可化为： 或 或 ，1644 13124 136+44解得： ，0或 43所求解集为： |0或 43（II）当 x- ， ）时，由 k-1 有：3x-10，3x+k0f （x）=1+k，3 13不等式 f（x）g（x）可变形为：1+kx+4，故 kx+3 对 恒成立，3， 13)即 ，解得 ，3+3 94而 k-1 ，故 1 94k 的取值范围是： (1，94【解析】（I）将 k=-3 代入，根据零点分段法去掉 绝对值，分别解不等式取交集； （II）根据 x 的范 围对 f（x）去掉绝对值，参变分离转化为求函数的最值问题，列出关于 k 的不等式，解出范围即可本题考查绝对值不等式的解法，以及与绝对值不等式有关的恒成立问题，属于中档题
