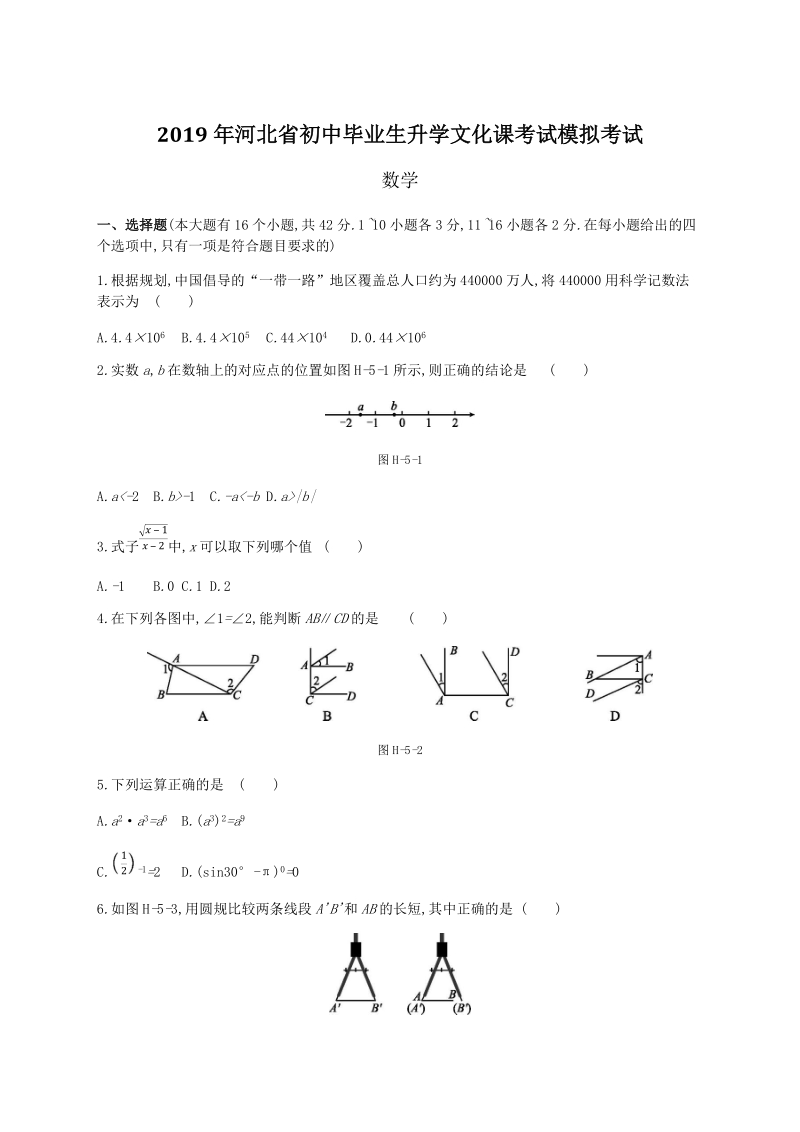
1、2019 年河北省初中毕业生升学文化课考试模拟考试数学一、选择题(本大题有 16 个小题,共 42 分 .110 小题各 3 分,11 16 小题各 2 分 .在每小题给出的四个选项中,只有一项是符合题目要求的)1.根据规划,中国倡导的“一带一路”地区覆盖总人口约为 440000 万人,将 440000 用科学记数法表示为 ( )A.4.4106 B.4.4105 C.44104 D.0.441062.实数 a,b 在数轴上的对应点的位置如图 H-5-1 所示,则正确的结论是 ( )图 H-5-1A.a-1 C.-a|b|3.式子 中, x 可以取下列哪个值 ( )12A.-1 B.0 C.1
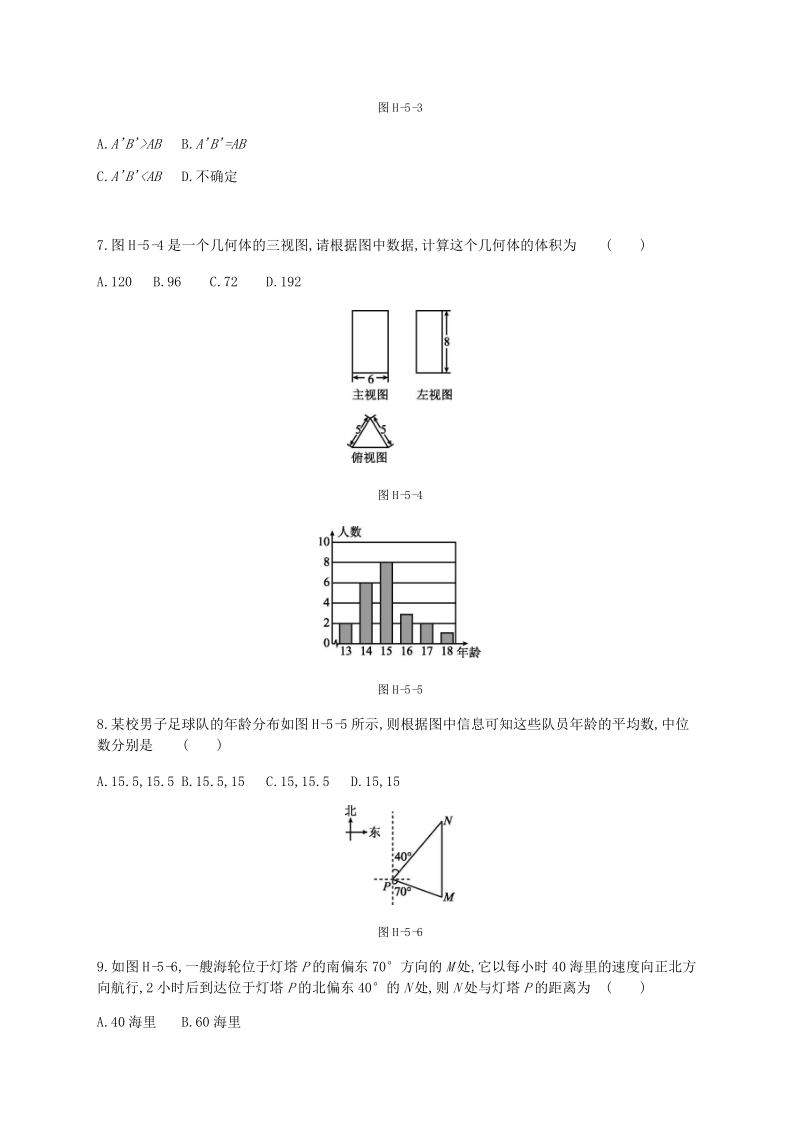
2、 D.24.在下列各图中,1 =2,能判断 AB CD 的是 ( )图 H-5-25.下列运算正确的是 ( )A.a2a3=a6 B.(a3)2=a9C. -1=2 D.(sin30-) 0=0126.如图 H-5-3,用圆规比较两条线段 AB和 AB 的长短,其中正确的是 ( )图 H-5-3A.ABAB B.AB=ABC.AB0)与 x 轴交于点 B、 C,与1y 轴交于点 E,且点 B 在点 C 的左侧 .(1)若抛物线过点 M(-2,-2),求实数 a 的值;(2)在(1)的条件下,解答下列问题: 求出 BCE 的面积; 在抛物线的对称轴上找一点 H,使 CH+EH 的值最小,直接写出
3、 H 点的坐标 .图 H-5-1525.(11 分)参考信息: 数学家皮克Georg Pick发现:假设正方形网格平面(小正方形边长为 1 个单位长度)上有一个格点多边形 P(即顶点全部是格点的多边形),那么其面积 S=I+ -1.其中 I 为多边形 P 内部所含的格点2数, E 是多边形 P 边界上的格点数 . 对于一个周长及边数为定值的多边形来说,当其成为正多边形时,面积最大 .在此基础上,请解决下列问题:(1)如图 H-5-16,每个小正方形的边长均为 1,在此格点多边形 ABCD 中, I= ,E= ,其面积为 . 图 H-5-16(2) 周长为 6 的六边形面积最大为 ,这个数值 1
4、3(填“大于”“等于”或5“小于”) . 一青蛙在如图 H-5-17 所示的 88 的正方形网格(每个小正方形的边长为 1)的格点上跳跃,青蛙每次所跳的最远距离为 ,青蛙从点 A 开始连续跳六次正好跳回到点 A,则所构成的封闭图形的面积5的最大值是多少?并画出跳跃路线 .图 H-5-1726.(12 分)如图 , ABC 为等边三角形, ADE ABC,相似比为 k 1,点 D 在 AB上,点 E 在 AC 上 .(1)证明: DE BC;(2)将 ADE 绕点 A 逆时针旋转角 至 AMN 的位置, MN 与 AC 交于点 F. 如图 ,当 AM BC 时,请判断 AC 与 MN 的位置关系
5、,并说明理由; 若四边形 AMCN 为菱形,如图 ,求旋转角 及 k 的值; 如图 ,当直线 MN 过点 B 时,求 k 与旋转角 (0 60)之间的关系式 .图 H-5-18参考答案1.B 2.B3.C 【解析】 式子 在实数范围内有意义, x- 10,解得 x1,且使得分母 x-2 不能为 0,1故答案为 C.4.D 【解析】 选项 A、B、C 中的1 与2 都不是直线 AB、 CD 形成的同位角,所以不能判断AB CD.选项 D 中,1 与2 是直线 AB、 CD 被直线 AC 所截形成的同位角, 1 =2, AB CD(同位角相等,两直线平行) .故选 D.5.C 【解析】 a2a3=
6、a5,(a3)2=a6,(sin30-) 0=1,选项 C 运算正确,故选 C.6.A7.B 【解析】 由三视图可以看出是一个三棱柱,体积等于底面积乘以高,所以 V= 8=96,所以642答案为 B.8.D 【解析】 根据图中信息可知这些队员年龄的平均数为:=15(岁),132+146+158+163+172+1812+6+8+3+2+1该足球队共有队员 2+6+8+3+2+1=22(人),则第 11 名和第 12 名队员的平均年龄即为年龄的中位数,即中位数为 15 岁,故选:D .9.D 【解析】 MN=240=80(海里), M=70, N=40, NPM=180- M- N=180-70
7、-40=70, NPM= M,NP=MN= 80 海里 .故选 D.10.C 【解析】 根据题意得: = 16-8k0,且 k0,解得: k2 且 k0,则 k 的非负整数值为 1 或2.故选:C .11.D 【解析】 当 a0 时, -a0,即 -a 是非负数,故 A 错误; -a 是 a 的相反数,故 B 错误;当 a=0时, -a 与 a 相等,故 C 错误;根据“一个负数的绝对值是它的相反数”,知 D 正确 .12.B 【解析】 如图,由题意可得: AOB=120,OA=4,在 Rt AOD 中,可得: AOD=60, DAO=30,OD= AO= 4=2,12 12可得:矢 =4-2
8、=2,由 AD=AOsin60=4 =2 ,可得:弦 =2AD=22 =4 ,32 3 3 3所以弧田面积 = (弦 矢 +矢 2)= (4 2+22)=4 +29(平方米 ).故选:B .12 12 3 313.D14.A 【解析】 平行四边形 ABCD, B= D= AMN,MN BC,AM=DA , 四边形 AMND 为菱形,MN=AM. 故选 A.15.B16.C 【解析】 如图,连接 AC, 四边形 ABCD 为菱形, B=60, AEF 是正三角形, 1 + EAC=60,2 + EAC=60, 1 =2,易知 ABC 和 ACD 为等边三角形, 3 =60,AC=AB, 在 AB
9、E 和 ACF 中, 1= 2,=, = 3, ABE ACF(ASA),S ABE=S ACF,S 四边形 AECF=S AEC+S ACF=S AEC+S ABE=S ABC,是定值,作 AH BC 于 H 点,在 Rt AHB 中, B=60,sinB= ,AB=BC= 8,AH=AB sinB=8 =4 ,S 四边形 AECF=S ABC= AHBC= 4 8=16 .32 3 12 12 3 3由“垂线段最短”可知:当正三角形 AEF 的边 AE 与 BC 垂直时,边 AE 最短, AEF 的面积会随着 AE 的变化而变化, 当 AE=AH 时,正三角形 AEF 的面积最小,又 S
10、CEF=S 四边形 AECF-S AEF, 此时 CEF 的面积最大,S CEF=S 四边形 AECF-S AEF=16 - (4 )2=4 .334 3 317. 18.11319.(1)(1,0) (2)(2, ) 【解析】 由题意得,小球第一次碰到三角形的边时的点 D1的坐标是3(1,0),小球第二次碰到三角形的边时的点 D2的坐标是(2, ),小球第三次碰到三角形的边时的点3D3的坐标是(1, ),小球第四次碰到三角形的边时的点 D4的坐标是(2,0),小球第五次碰到三角形的3边时的点 D5的坐标是 , ,小球第六次碰到三角形的边时的点 D6的坐标是 , ,点 D6与点 D 重52 3
11、2 12 32合, 每六次一个循环, 20186=3362, 点 D2018的坐标是(2, ).320.解:(1) = = ;2 24+42 2 (2)2(1)211- = = .2 分21(1)(2)1 11所以,小明擦掉的代数式为 ; 4 分11(2)要使原式 1- 有意义,11 24+42需保证所有的分母(包括除式的分子)都不等于 0,即 a-10, a(a-1)0,且( a-2)20,则 a1,0,2 .因为 a 为绝对值小于 3 的整数,所以 a=-1 或 -2. 6 分当 a=-1 时,原式 = = ;11213当 a=-2 时,原式 = = . 8 分2221221.解:(1)画
12、树状图法:或列表法:十位数个位数 1 2 3 4 512 123 13 234 14 24 345 15 25 35 456 16 26 36 46 563 分根据列表法(画树状图法)知共有 15 种等可能的情况,其中抽取的“两位递增数”能被 3 整除的有12、15、24、36、45,共 5 种情况, 抽取的“两位递增数”能被 3 整除的概率 = = ; 5 分51513(2)抽取的“两位递增数”的个位数字与十位数字之积能被 3 整除的有13、16、23、26、34、35、36、46、56 共 9 种情况, 抽取的“两位递增数”的个位数字与十位数字之积能被 3 整除的概率 = = . 9 分9
13、153522.解:(1)当 0 x8 时,设水温 y()与开机时间 x(分)的函数关系式为: y=kx+b, 1 分依据题意,得 解得:=20,8+=100, =10,=20,故此函数解析式为: y=10x+20; 4 分(2)在水温下降过程中,设水温 y()与开机时间 x(分)的函数关系式为: y= ,依据题意,得:100 = ,即 m=800,故 y= , 5 分8 800当 y=20 时,20 = ,解得: t=40; 6 分800(3) 45-40=58, 当 x=5 时, y=105+20=70. 8 分答:小明散步 45 分钟回到家时,饮水机内的温度约为 70 .9 分23.解:(
14、1)证明:如图 ,连接 OC,则 OC EF,且 OC=OA, 1 分 OCA= OAC.AD EF,OC AD. OCA= CAD, CAD= OAC. 3 分即 CAD= BAC. 4 分(2)与 CAD 相等的角是 BAG. 5 分证明如下:如图 ,连接 BG. 四边形 ACGB 是 O 的内接四边形, ABG+ ACG=180. 6 分D ,C,G 共线, ACD+ ACG=180. ACD= ABG.AB 是 O 的直径, BAG+ ABG=90.AD EF, CAD+ ACD=90, 8 分 CAD= BAG. 9 分24.解:(1)将点 M(-2,-2)的坐标代入抛物线解析式,得
15、 -2= (-2-2)(-2+a),解得 a=4.2 分1(2) 由(1)得 y= (x-2)(x+4),当 y=0 时,0 = (x-2)(x+4),解得 x1=2,x2=-4.14 14 点 B 在点 C 的左侧, B (-4,0),C(2,0). 4 分当 x=0 时, y= (0-2)(0+4),14解得 y=-2.E (0,-2).7 分 BCE 的面积 = 62=6. 8 分12H -1,- .10 分3225.解:(1) I=13,E=9,面积为 16.5. 3 分(2) ; 5 分1532小于 . 7 分 所构成的封闭图形的面积的最大值是 12. 9 分跳跃路线如图所示(只要构
16、成的封闭图形的面积是 12,即 I=10,其他路线也可) . 11 分26.解:(1)证明: ADE ABC, ADE= B,DE BC. 2 分(2)AC MN. 3 分证明:如图 ,延长 AM 交 BC 于 D, ABC 是等边三角形, AB=AC , BAC=60, DAC=30,又 AMN=60, AFM=90,即 AC MN.5 分 四边形 AMCN 为菱形,AC 平分 MAN, MAC=30, BAM=30,= 30, 7 分 四边形 AMCN 为菱形, AF= AC,AC MN,12在 Rt AFM 中,cos30 = ,AF= AM, AM= AC,AC= AM,32 32 12 3 ABC 为等边三角形, AC=AB ,AB= AM,3 ADE 与 ABC 的相似比为 k 1, = ,AM=kAB,k= . 9 分1 33 如图 ,过 A 作 AH MN 于 H, AMN 是等边三角形,AH=AM cos30= AM,32在 Rt AHB 中, BAH=+ 30, cos BAH=cos(+ 30)= ,AH=AB cos(+ 30),AB cos(+ 30)= AM,32由 得: AM=kAB, cos(+ 30)= k. 12 分32
