1、2019 年四川省中考数学信息卷1 选择题（36 分）1 的相反数是（ ）A B6 C6 D2.如图是由 6 个大小相同的小立方体搭成的几何体，从正面看到的图形是（ ）A B C D3.下列计算正确的是（ ）Ax 4+x42x 8 Bx 3x2x 6C（x 2y） 3x 6y3 D（xy） 2x 2 一 y24.将不等式组 的解集表示在数轴上，下面表示正确的是（ ）A BC D5.我国人工智能在 2017 年迎来发展的“应用元年“，预计 2020 年中国人工智能核心产业规模超 1500 亿元，将 150000000000 这个数用科学记数法表示为（ ）A1510 10 B1.510 11 C1
2、.510 12 D0.1510 126.若一个扇形的弧长 l ，面积 S2 ，则这个扇形的圆心角为（ ）A50 B60 C70 D807.如图，在平面直角坐标系中，过反比例函数 y （k0，0）的图象上一点 A 作AB x 轴于 B，连结 AO，过点 B 作 BCAO 交 y 轴于点 C若点 A 的纵坐标为 4，且tan BCO ，则 k 的值为（ ）A6 B12 C24 D248.如图所示，ABC 中，AB AC，过 AC 上一点作 DEAC，EFBC，若BDE140，则DEF （ ）A55 B60 C65 D709.如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为 1，
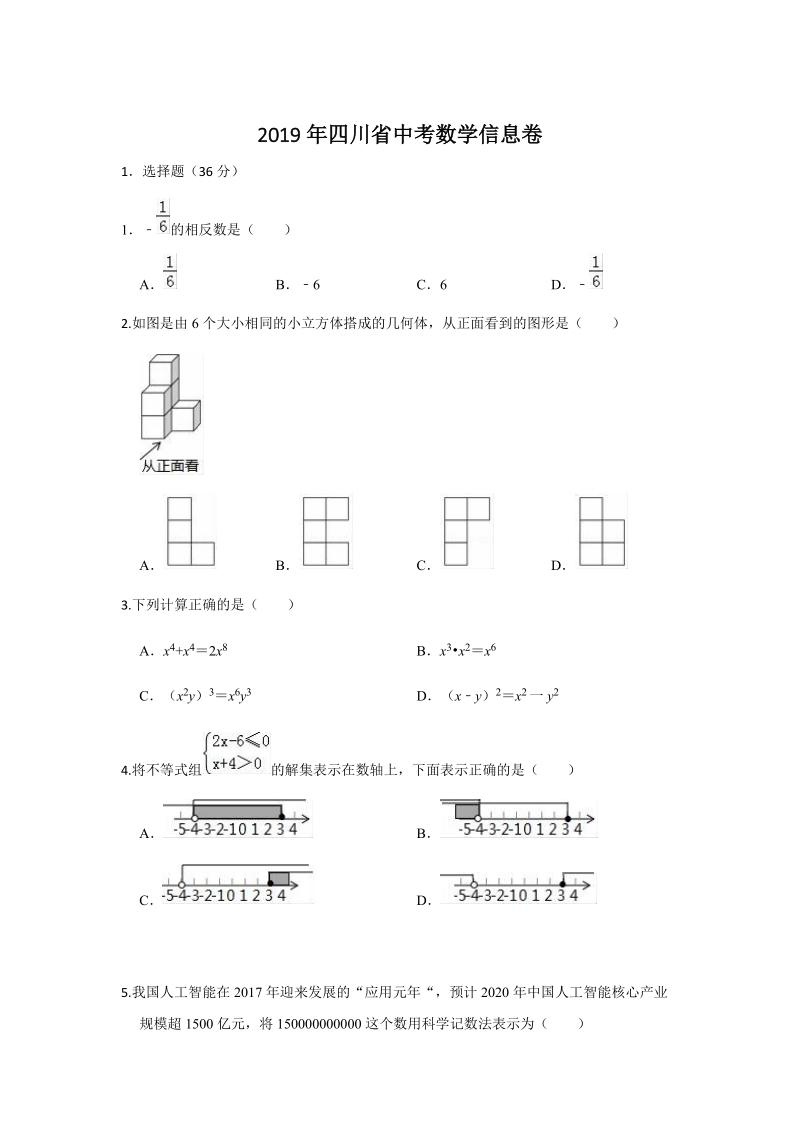
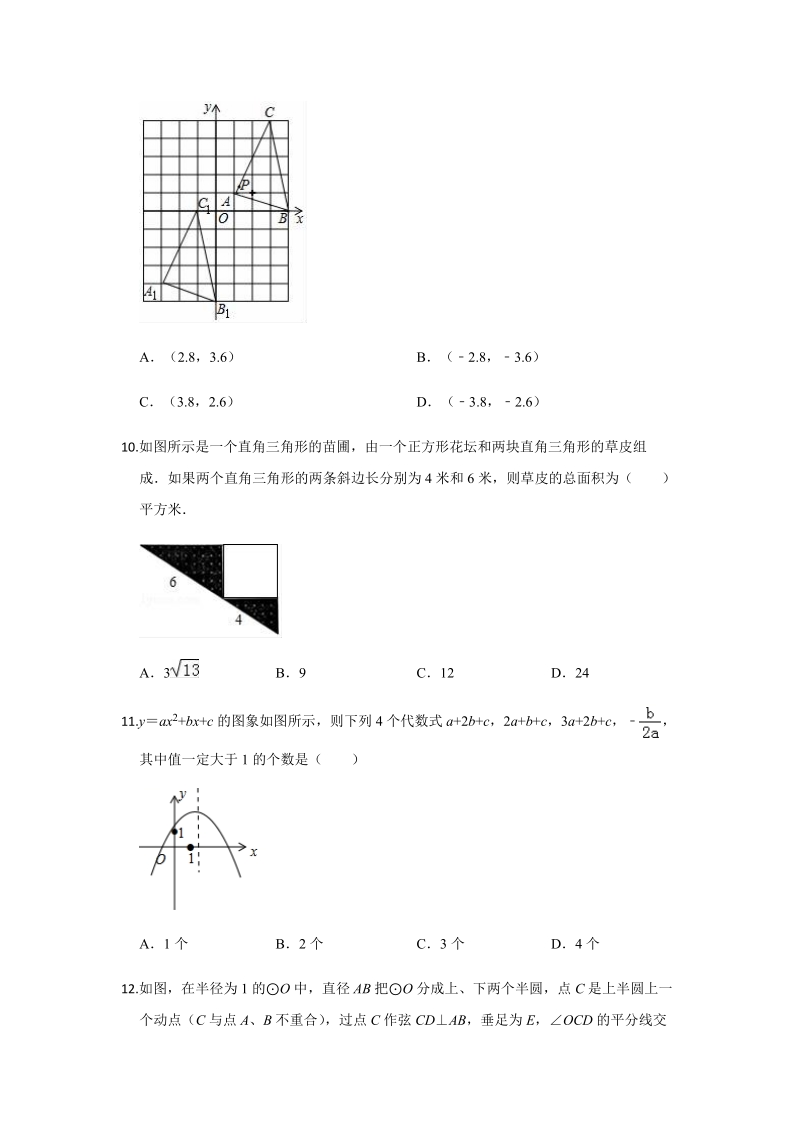
3、ABC经过平移后得到A 1B1C1，若 AC 上一点 P（1.2，1.4）平移后对应点为 P1，点 P1 绕原点顺时针旋转 180，对应点为 P2，则点 P2 的坐标为（ ）A（2.8，3.6） B（2.8，3.6）C（3.8，2.6） D（3.8 ，2.6）10.如图所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的草皮组成如果两个直角三角形的两条斜边长分别为 4 米和 6 米，则草皮的总面积为（ ）平方米A3 B9 C12 D2411.yax 2+bx+c 的图象如图所示，则下列 4 个代数式 a+2b+c，2a+b+c，3a+2b+c， ，其中值一定大于 1 的个数是（ ）A
4、1 个 B2 个 C3 个 D4 个12.如图，在半径为 1 的O 中，直径 AB 把 O 分成上、下两个半圆，点 C 是上半圆上一个动点（C 与点 A、B 不重合） ，过点 C 作弦 CDAB ，垂足为 E，OCD 的平分线交O 于点 P，设 CEx ，AP y，下列图象中，最能刻画 y 与 x 的函数关系的图象是（ ）A BC D2 填空题（15 分）13.已知一组数据：6，2，8，x ，7，它们的平均数是 6，则这组数据的中位数是 14.在不透明的盒子中装有 6 个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同任意摸出一个棋子，摸到黑色棋子的概率是 ，则白色棋子的个数是 15.一个正多
5、边形的每个内角都是 150，则它是正 边形16.在矩形 ABCD 中，AECF AD1，BE 的垂直平分线过点 F，交 BE 于点 H，交 AB于点 G，则 AB 的长度为 17.如图，正方形 ABCD 中，点 E 是 AD 边的中点，BD，CE 交于点 H，BE、AH 交于点G，则下列结论：AG BE；BG 4GE； SBHE SCHD；AHB EHD其中正确的答案是 ；3解答题（69 分）18. （5 分）计算：|1 3 | +（ ） 1 +2sin3019.（6 分）如图，E 是平行四边形 ABCD 的边 BA 延长线上一点，AEAB，连结AC、DE、CE（1）求证：四边形 ACDE 为
6、平行四边形（2）若 ABAC ，AD 4，CE6，求四边形 ACDE 的面积20.（12 分）某学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级一班学生即将穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为 6 种型号）根据以上信息，解答下列问题：（1）该班共有多少名学生？（2）请通过计算补全条形统计图；（3）请直接写出该班学生所穿校服型号众数是 ，中位数是 ；（4）若该校九年级有学生 5010 人，请你估计穿 175 型校服的学生约有多少人？21.（10 分）如图在平面直角坐标系 xOy 中，一次函数 y2x2 的图象与函数y
7、 （k 0）的图象有交点为 A（m ，2），与 y 轴交于点 B（1）求反比例函数的解析式；（2）若函数 y 在第一象限的图象上有一点 P，且POB 的面积为 6，求点 P 坐标22.（10 分）目前节能灯已基本普及，节能还环保，销量非常好，某商场计划购进甲、乙两种型号节能灯共 1200 只，这两种节能灯的进价、售价如表所示：进价（元/只） 售价（元/只）甲型 25 30乙型 45 60（1）商场应如何进货，使进货款恰好为 46000 元？（2）若商场销售完节能灯后获利不超过进货价的 30%，至少购进甲种型号节能灯多少只？23.（12 分）如图，已知O 的直径 CD8，A，B 为圆周上两点，且
8、四边形 OABC 是平行四边形，直线 EF 切O 于点 A，分别交 CD、CB 的延长线于点 E、F，AO 与 BD 交于G 点（1）求证：EFBD ；（2）求 AE 的长24.（14 分）如图，抛物线 yax 2+（a+4）x+4（a0）与 x 轴交于点 A（3，0），与 y 轴交于点 B，在 x 轴上有一动点 E（m ，0）（0m 3），过点 E 作 x 轴的垂线交直线 AB于点 N，交抛物线于点 P，过点 P 作 PMAB 于点 M（1）求 a 的值和直线 AB 的函数表达式；（2）设PMN 的周长为 C1， AEN 的周长为 C2，若 2，求 m 的值；（3）在 y 轴上有一点 F（0
9、，t ），若AFB45，请直接写出 t 的取值范围2019 年四川省中考数学信息卷4 选择题（36 分）1 的相反数是（ ）A B6 C6 D【分析】直接利用相反数的定义分析得出答案【解答】解： +（ ）0， 的相反数是： 故选：A【点评】此题主要考查了相反数，正确把握相反数的定义是解题关键2.如图是由 6 个大小相同的小立方体搭成的几何体，从正面看到的图形是（ ）A B C D【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中【解答】解：从正面看到的图形是故选：A【点评】本题考查了三视图的知识 注意主视图是指从物体的正面看物体3.下列计算正确的是（ ）Ax 4+x42
10、x 8 Bx 3x2x 6C（x 2y） 3x 6y3 D（xy） 2x 2 一 y2【分析】根据合并同类项法则，同底数幂的乘法，幂的乘方和积的乘方，完全平方公式分别求出每个式子的值，再逐个判断即可【解答】解：A、x 4+x42x 4，故本选项不符合题意；B、x 3x2x 5，故本选项不符合题意；C、（x 2y） 3x 6y3，故本选项符合题意；D、（xy） 2x 22xy+y 2，故本选项不符合题意；故选：C【点评】本题考查了合并同类项法则，同底数幂的乘法，幂的乘方和积的乘方，完全平方公式等知识点，能正确求出每个式子的值是解此题的关键4.将不等式组 的解集表示在数轴上，下面表示正确的是（ ）
11、A BC D【分析】首先解出两个不等式的解集；根据在数轴上表示不等式解集的方法分别把每个不等式的解集在数轴上表示出来即可【解答】解：解不等式 得， x3解不等式 得， x4在数轴上表示为：故选：A【点评】本题考查的是在数轴上表示不等式 组的解集，把每个不等式的解集在数轴上表示出来（，向右画；，向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集有几个就要几个在表示解集时“”，“”要用实心圆点表示；“”，“”要用空心圆点表示5.我国人工智能在 2017 年迎来发展的“应用元年“， 预计 2020 年中国人工智能核心产业规模超
12、1500 亿元，将 150000000000 这个数用科学记数法表示为（ ）A1510 10 B1.510 11 C1.510 12 D0.1510 12【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值10 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：1500000000001.510 11，故选：B【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n 的形式，其中 1|a| 10 ，n 为整数，表示时关键要正确确定 a
13、的值以及 n 的值6.若一个扇形的弧长 l ，面积 S2 ，则这个扇形的圆心角为（ ）A50 B60 C70 D80【分析】设扇形的半径为 r，圆心角为 n利用扇形面积公式求出 r，再利用弧长公式求出圆心角即可【解答】解：设扇形的半径为 r，圆心角为 n由题意： r2，r3， ，n80，故选：D【点评】本题考查扇形的面积的计算，弧长公式等知识，解题的关键是掌握基本知识，属于中考常考题型7.如图，在平面直角坐标系中，过反比例函数 y （k0，0）的图象上一点 A 作AB x 轴于 B，连结 AO，过点 B 作 BCAO 交 y 轴于点 C若点 A 的纵坐标为 4，且tan BCO ，则 k 的值
14、为（ ）A6 B12 C24 D24【分析】先证明四边形 OABC 是平行四边形，得出OABBCO，那么tan OAB tanBCO ，由 AB4，求出 OB 6，得到 A（6，4），代入y ，即可求出 k 的值【解答】解：ABx 轴，ABOC，BCAO，四边形 OABC 是平行四边形，OABBCOtanBCO ，tanOAB ，又 AB4，OB6，A（6，4）点 A 在反比例函数 y （k 0，0）的图象上，k6424故选：C【点评】本题考查了反比例函数图象上点的坐标特征，平行四边形的判定与性质，锐角三角函数定义，难度适中求出 A 点坐标是解题的关键8.如图所示，ABC 中，AB AC，过
15、AC 上一点作 DEAC，EFBC，若BDE140，则DEF （ ）A55 B60 C65 D70【分析】由 DEAC，BDE140，可计算出A，再利用等腰三角形的性质求出C，最后利用 EFBC 及同角的余角相等得到 DEF 的度数【解答】解：DEAC，BDE140，A50，又ABAC，C 65 ，EFBC，DEFC65所以 A 错，B 错，C 对，D 错故选 C【点评】考查了垂直的性质，等腰三角形的性质和三角形的外角性质9.如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为 1，ABC经过平移后得到A 1B1C1，若 AC 上一点 P（1.2，1.4）平移后对应点为 P1，
16、点 P1 绕原点顺时针旋转 180，对应点为 P2，则点 P2 的坐标为（ ）A（2.8，3.6） B（2.8，3.6）C（3.8，2.6） D（3.8 ，2.6）【分析】由题意将点 P 向下平移 5 个单位，再向左平移 4 个单位得到 P1，再根据 P1 与 P2关于原点对称，即可解决问题；【解答】解：由题意将点 P 向下平移 5 个单位，再向左平移 4 个单位得到 P1，P（1.2，1.4），P 1（2.8，3.6），P 1 与 P2 关于原点对称，P 2（2.8，3.6），故选：A【点评】本题考查坐标与图形变化，平 移变换，旋转变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，
17、属于中考常考题型10.如图所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的草皮组成如果两个直角三角形的两条斜边长分别为 4 米和 6 米，则草皮的总面积为（ ）平方米A3 B9 C12 D24【分析】先根据相似三角形的判定定理得出AMBCBE，故可得 出 的值，设CEx ，则 BC2x，在 RtCBE 中根据勾股定理求出 x 的值，故可得出CE，AB BC， AM2AB 的值，再根据 S 草皮 S CBE +SAMB ，即可得出结论【解答】解：MDE 是直角三角形，四边形 ABCD 是正方形，MAB BCE90，M+ ABM 90，ABM+ CBE90，MCBE，AMB CBE，
18、 ，MB6，BE4， ，ABBC， ，设 CE2x，则 BC3x ，在 RtCBE 中，BE2BC 2+CE2，即 42（3x） 2+（2x） 2，解得 x ，CE ，ABBC ，AM AB ，S 草皮 S CBE +SAMB + 12故选：C【点评】本题考查了相似三角形的应用，解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题11.yax 2+bx+c 的图象如图所示，则下列 4 个代数式 a+2b+c，2a+b+c，3a+2b+c， ，其中值一定大于 1 的个数是（ ）A1 个 B2 个 C3 个 D4 个【解答】解：由 yax 2+bx+c 的图象可
19、得：开口向下，故 a0；与 y 轴的交点在（0，1）的上方，故 c1；对称轴在 y 轴右侧，且 a0 故 b0；由图象可知当 x1 时，y a+b+c1a+2b+ca+b+c +b1；对称轴 x 1，b2a，2a+b0，2a+b+c0+c1；3a+2b+c（2a+ b）+（a+ ）+ +c0+ +0+cc 1；综上所述，值一定大于 1 的个数是 4 个故选：D12.如图，在半径为 1 的O 中，直径 AB 把 O 分成上、下两个半圆，点 C 是上半圆上一个动点（C 与点 A、B 不重合） ，过点 C 作弦 CDAB ，垂足为 E，OCD 的平分线交O 于点 P，设 CEx，AP y，下列图象中
20、，最能刻画 y 与 x 的函数关系的图象是（ ）A BC D【解答】解：连接 OP，OCOP，OCPOPCOCPDCP，CDAB，OPCDCPOPCDPOABOAOP 1，APy （0x 1） 故选：A5 填空题（15 分）13.已知一组数据：6，2，8，x ，7，它们的平均数是 6，则这组数据的中位数是 【分析】首先根据平均数为 6 求出 x 的值，然后根据中位数的概念求解【解答】解：数据 6，2，8，x，7 的平均数是 6，6+2+8+x+765，解得：x7，这组数据按照从小到大的顺序排列为：2，6，7，7，8，则中位数为 7；故答案为：7【点评】本题考查了中位数和平均数的知识，将一组数据
21、按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位 数；平均数是指在一组数据中所有数据之和再除以数据的个数14.在不透明的盒子中装有 6 个黑色棋子和若干个白色棋子，每个棋子除颜色外都相同任意摸出一个棋子，摸到黑色棋子的概率是 ，则白色棋子的个数是 【分析】设盒子中白色棋子有 x 个，根据概率公式列出关于 x 的方程，解之可得【解答】解：设盒子中白色棋子有 x 个，根据题意，得： ，解得：x24，经检验：x24 是原分式方程的解，所以白色棋子有 24 个，故答案为：24【点评】本
22、题考查了概率公式，用到的知识点为：概率所求情况数与总情况数之比15.一个正多边形的每个内角都是 150，则它是正 边形【分析】首先根据内角度数计算出外角度数，再用外角和 360除以外角度数即可【解答】解：一个正多边形的每个内角为 150，它的外角为 30，3603012，故答案为：十二【点评】此题主要考查了多边形的内角与外角，关键是掌握内角与外角互为邻补角16.在矩形 ABCD 中，AECF AD1，BE 的垂直平分线过点 F，交 BE 于点 H，交 AB于点 G，则 AB 的长度为 【分析】如图作 EMBC 于 M，连接 EF首先证明四边形 ABME 是矩形，在 RtEFM 中，利用勾股定理
23、求出 EM 即可解决问题；【解答】解：如图作 EMBC 于 M，连接 EF四边形 ABCD 是矩形，AABMEMB90，四边形 ABME 是矩形，AEBM1，ADBC3 ，GF 垂直平分 BE，BFEF2，MF BF BM1，在 Rt EFM 中， EM ，ABEM ，故答案为 【点评】本题考查矩形的性质和判定、线段的垂直平分线的性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题17.如图，正方形 ABCD 中，点 E 是 AD 边的中点，BD，CE 交于点 H，BE、AH 交于点G，则下列结论：AG BE；BG 4GE； SBHE S CHD；AHB EHD 其中正
24、确的答案是 ；【分析】首先根据正方形的性质证得BAECDE，推出ABEDCE，再证ADH CDH，求得 HADHCD ，推出ABE HAD ；求出ABE+ BAG 90；最后在AGE 中根据三角形的内角和是 180求得AGE90即可得到 正确根据 tanABEtanEAG ，得到 AG BG，GE AG，于是得到 BG4EG，故 正确；根据 ADBC ，求出 SBDE S CDE ，推出 SBDE S DEHS CDE S DEH ，即； SBHE S CHD ，故正确；由AHDCHD ，得到邻补角和对顶角相等得到AHBEHD，故正确；【解答】证 明：四边形 ABCD 是正方形，E 是 AD
25、边上的中点，AEDE ，ABCD，BADCDA90，BAE CDE（SAS），ABE DCE，四边形 ABCD 是正方形，ADDC，ADBCDB45，DHDH，ADH CDH（SAS），HAD HCD，ABE DCEABE HAD，BADBAH+DAH90，ABE +BAH90，AGB1809090，AGBE，故正确；tanABEtanEAG ，AG BG，GE AG，BG4EG ，故 正确；ADBC，S BDE S CDE ，S BDE S DEH S CDE S DEH ，即；S BHE S CHD ，故正确；ADH CDH，AHD CHD，AHBCHB，BHCDHE，AHBEHD，故正确
26、；故答案为【点评】本题主要考查了正方形的性质及全等三角形的判定与性质，三角形的面积公式，解答本题要充分利用正方形的特殊性质：四边相等，两两垂直； 四个内角相等，都是 90 度； 对角线相等，相互垂直，且平分一组对角6解答题（69 分）19. （5 分）计算：|1 3 | +（ ） 1 +2sin30【分析】直接利用负指数幂的性质以及二次根式的性质和绝对值的性质分别化简得出答案【解答】解：原式3 13 +2+12【点评】此题主要考查了实数运算，正确化简各数是解题关键19.（6 分）如图，E 是平行四边形 ABCD 的边 BA 延长线上一点，AEAB，连结AC、DE、CE（1）求证：四边形 ACD
27、E 为平行四边形（2）若 ABAC ，AD 4，CE6，求四边形 ACDE 的面积【分析】（1）由平行四边形的性质得出 ABCD，ABCD，即 AECD，证出AE CD，由平行四边形的判定定理即可得出四边形 ACDE 为平行四边形（2）由平行四边形的性质得出 AD、CE 互相平分，证出 ACCD，证出四边形 ACDE是菱 形，得出 ADCE，由菱形面积公式即可求出结果【解答】（1）证明：四边形 ABCD 是平行四边形，ABCD，AB CD ，即 AECD，AEAB，AECD，四边形 ACDE 为平行四边形（2）解：由（1）得：四边形 ACDE 为平行四边形，AD、CE 互相平分，ABAC，CD
28、AB ，ACCD，四边形 ACDE 是菱形，ADCE，四边形 ACDE 的面积 ADCE 4612【点评】本题考查了平行四边形的判定与性质、菱形的判定与性质、等腰三角形的判定与性质等知识；熟练掌握平行四边形的判定与性质，证明四边形 ACDE 为菱形是解题的关键20.（12 分）某学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级一班学生即将穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为 6 种型号）根据以上信息，解答下列问题：（1）该班共有多少名学生？（2）请通过计算补全条形统计图；（3）请直接写出该班学生所穿校服型号众数是
29、，中位数是 ；（4）若该校九年级有学生 5010 人，请你估计穿 175 型校服的学生约有多少人？【分析】（1）根据穿 165 型的人数与所占的百分比列式进行计算即可求出学生总人数；（2）总人数乘以 175 型所占的百分比计算其对应人数，根据各型号人数之和等于总人数求出 185 型的人数，然后补全统计图即可；（3）根据众数的定义以及中位数的定义解答；（4）总人数乘以样本中穿 175 型校服的学生人数所占比例【解答】解：（1）该班学生的总人数为 1530%50（名）；（2）175 的人数为 5020%10（名），185 型的学生人数为：503151510550482（名），补全统计图如图所示（3
30、）165 型和 170 型出现的次数最多，都是 15 次，故众数是 165 和 170；共有 50 个数据，第 25、 26 个数据都是 170，故中位数是 170故答案为：165 和 170，170；（4）估计穿 175 型校服的学生有 501020%1002（人）【点评】本题考查的是条形统计图和扇形统计图的综合运用读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小除此之外，本题也考查了平均数、中位数、众数的认识21.（10 分）如图在平面直角坐标系 xOy 中，一次函数 y2x2 的图象与函数y （k
31、0）的图象有交点为 A（m ，2），与 y 轴交于点 B（1）求反比例函数的解析式；（2）若函数 y 在第一象限的图象上有一点 P，且POB 的面积为 6，求点 P 坐标【分析】（1）通过一次函数求出 m，即求出 A 的坐标；然后通过把 A 坐标代入反比例函数，求反比例函数解析式；（2）先确定POB 的面积以 OB 为底，CP 为高；OB 的长是固定的，只需要 CP 的长度；点 P 在反比例函数图象上，将它代入反比例函数，从而求出 P（x， ）即CPx； 从而列出 SPOB 6，即 x6，并求出 y 值，从而确定 P 的坐标；【解答】解：（1）由已知得点 A（m ，2）在函数 y2x 2 图象
32、上，故 2m22，解得 m2，即 A（2，2）并且点 A（2，2）也在函数 y 的图象上，2 解得 k4，所以反比例函数 y（2）过点 P 作 CPy 轴；POB 的面积以 OB 为底，CP 为高；在函数 y2x2 中，当 x0 时，y2即 OB2，设函数 y （x0）图象上点 P（x， ）S POB 6解得：x6，则 y此时点 p（6， ）【点评】这题主要考查：反比例函数、一次函数、三角形的面积公式等；当有两个函数的时候，着重使用一次函数，体现了方程思想，综合性较强22.（10 分）目前节能灯已基本普及，节能还环保，销量非常好，某商场计划购进甲、乙两种型号节能灯共 1200 只，这两种节能灯
33、的进价、售价如表所示：进价（元/只） 售价（元/只）甲型 25 30乙型 45 60（1）商场应如何进货，使进货款恰好为 46000 元？（2）若商场销售完节能灯后获利不超过进货价的 30%，至少购进甲种型号节能灯多少只？【分析】（1）设购进甲型节能灯 x 只，乙型节能灯 y 只，根据“总数量为 1200 只、进货款恰好为 46000 元”列方程组求解可得；（2）设商场购进甲型节能灯 a 只，则购进乙型节能灯（1200a）只，根据“获利最多不超过进货价的 30%”列出不等式求解可得【解答】解：（1）设购进甲型节能灯 x 只，乙型节能灯 y 只，根据题意，得： ，解得： ，答：购进甲型节能灯 4
34、00 只，乙型节能灯 800 只，进货款恰好为 46000 元；（2）设商场购进甲型节能灯 a 只，则购进乙型节能灯（120 0a）只，由题意，得：（3025）a+（6045）（1200a）25a+45（1200a）30% ，解得：a450答：至少购进甲种型号节能灯 450 只【点评】此题主要考查了二元一次方程和一元一次不等式的应用，关键是正确理解题意，找出题目中的等量关系和不等关系，设出未知数，列出方程与不等式23.（12 分）如图，已知O 的直径 CD8，A，B 为圆周上两点，且四边形 OABC 是平行四边形，直线 EF 切O 于点 A，分别交 CD、CB 的延长线于点 E、F，AO 与
35、BD 交于G 点（1）求证：EFBD ；（2）求 AE 的长【分析】（1）利用圆周角定理得到DB C90，再利用平行四边形的性质得 AOBC ，所以 BDOA ，再根据切线的性质得出 OAEF，所以 OAEF，于是得到 EFBD；（2）连接 OB，如图，利用平行四边形的性质得 OABC，则 OBOCBC ，于是可判断OBC 为等边三角形，所以C60，易得AOE C60，然后在 RtOAE中利用正切的定义可求出 AE 的长【解答】（1）证明：CD 为直径，DBC90，BDBC，四边形 OABC 是平行四边形，AOBC，BDOA ，直线 EF 切O 于点 A，OAEF，EFBD ；（2）解：连接 OB，如图，四边形 OABC 是平行四边形，OABC，而 OBOCOA，OBOCBC，OBC 为等边三角形，C60，AOEC60，在 Rt OAE 中，tan AOE ，AE3tan603
