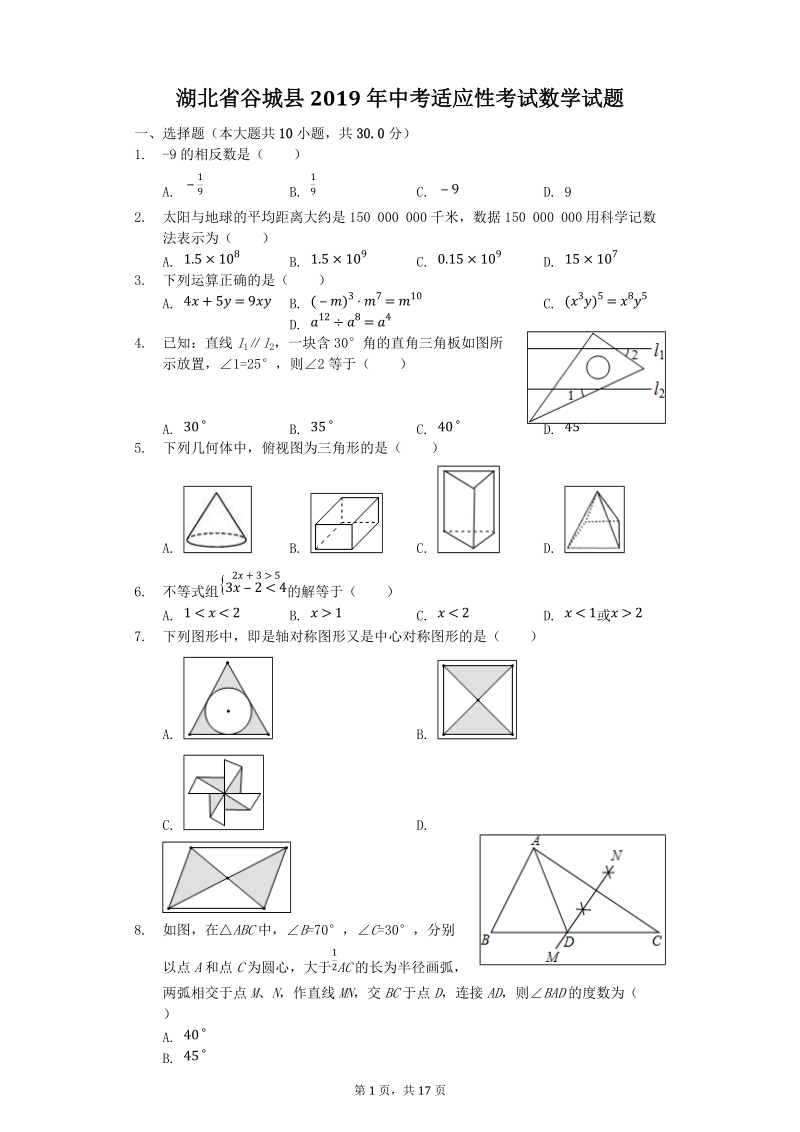
1、第 1 页，共 17 页湖北省谷城县 2019 年中考适应性考试数学试题一、选择题（本大题共 10小题，共 30.0分）1. -9的相反数是（ ）A. B. C. D. 919 19 92. 太阳与地球的平均距离大约是 150 000 000千米，数据 150 000 000用科学记数法表示为（ ）A. B. C. D. 1.5108 1.5109 0.15109 151073. 下列运算正确的是（ ）A. B. C. 4+5=9 ()37=10 (3)5=85D. 128=44. 已知：直线 l1 l2，一块含 30角的直角三角板如图所示放置，1=25，则2 等于（ ）A. B. C. D.
2、 30 35 40 455. 下列几何体中，俯视图为三角形的是（ ）A. B. C. D. 6. 不等式组 的解等于（ ）2+35321 27. 下列图形中，即是轴对称图形又是中心对称图形的是（ ）A. B. C. D. 8. 如图，在 ABC中， B=70， C=30，分别以点 A和点 C为圆心，大于 AC的长为半径画弧，12两弧相交于点 M、 N，作直线 MN，交 BC于点 D，连接 AD，则 BAD的度数为（ ）A. 40B. 45第 2 页，共 17 页C. 50D. 609. 在二次函数 y=-x2+2x+1的图象中，若 y随 x的增大而增大，则 x的取值范围是（ ）A. B. C.
3、 1 110. 如图， O的直径 CD过弦 EF的中点 G， DCF=20，则 EOD等于（ ）A. 10B. 20C. 40D. 80二、填空题（本大题共 6小题，共 18.0分）11. 计算： - =_273212. 孙子算经是中国古代重要的数学著作，其中有一段文字的大意是：甲、乙两人各有干钱，如果甲得到乙所有钱的一半，那么甲共有 48文；如果乙得到甲所有钱的 ，那么乙共有钱 48文，甲、乙二人原来各有多少钱？试求甲原有_文23钱13. “五一”节前，小兵、小军与小强三家准备从枣阳汉城、襄阳唐城两个景点中选择一个景点在节日期间去游玩，小兵、小军与小强通过抽签方式确定游玩景点，则三家投到同一
4、景点游玩的概率是_14. 在一次函数 y=kx+2中，若 y随 x的增大而增大，则它的图象不经过第_象限15. 劳技课上小敏拿出了一个腰长为 8厘米，底边为 6厘米的等腰三角形，她想用这个等腰三角形加工成一个边长比是 1：2 的平行四边形，平行四边形的一个内角恰好是这个等腰三角形的底角，平行四边形的其它顶点均在三角形的边上，则这个平行四边形的较短的边长为_16. 如图，在矩形纸片 ABCD中， AB=5cm， BC=10cm， CD上有一点 E， ED=2cm， AD上有一点 P， PD=3cm，过 P作 PF AD交 BC于 F，将纸片折叠，使 P点与 E点重合，折痕与 PF交于 Q点，则
5、PQ的长是_ cm三、计算题（本大题共 1小题，共 6.0分）17. 先化简，再求值：（ - ） ，其中 a= + ， b= - 2+ 2+ 2 3 2 3四、解答题（本大题共 8小题，共 66.0分）第 3 页，共 17 页18. 某校九年级两个班，各选派 10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：九（1）班：88，91，92，93，93，93，94，98，98，100；九（2）班：89，93，93，93，95，96，96，98，98，99通过整理，得到数据分析表如下：班级 最高分 平均分 中位数 众数 方差九（1）班 100 m 93 93 12九（2）班 99
6、95 n p 8.4（1）直接写出表中 m、 n、 p的值为： m=_， n=_， p=_；（2）依据数据分析表，有人说：“最高分在（1）班，（1）班的成绩比（2）班好”但也有人说（2）班的成绩要好请给出两条支持九（2）班成绩更好的理由；（3）学校确定了一个标准成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果九（2）班有一半的学生能够达到“优秀”等级，你认为标准成绩应定为_分，请简要说明理由19. 某商品现在的售价为每件 60元，每天可卖出 300件市场调查发现：如果调整价格，每降价 1元，每天可多卖出 20件已知商品的进价为每件 40元，如何定价既能使商品尽快卖出，又能使每天的利润达
7、到 6000元？20. 小明家所在居民楼的对面有一座大厦 AB， AB=80米，为测量这座居民楼与大厦之间的距离，小明从自己家的窗户 C处测得大厦顶部 A的仰角为37，大厦底部 B的俯角为 48求小明家所在居民楼与大厦的距离 CD的长度（结果保留整数）（参考数据：3735， 3734， 48710， 481110）第 4 页，共 17 页21. 如图，在平面直角坐标系 xOy中，一次函数 y1=k1x+1的图象与 y轴交于点 A，与x轴交于点 B，与反比例函数 y2= 的图象分别交于点 M、 N，已知 AOB的面积为21，点 M的纵坐标为 2（1）求一次函数与反比例函数的解析式；（2）直接写出
8、 y1 y2时 x的取值范围22. 已知：如图，在锐角 MAN的边 AN上取一点 B，以 AB为直径的半圆 O交 AM于C，交 MAN的角平分线于 E，过点 E作 ED AM，垂足为 D，反向延长 ED交 AN于F（1）猜想 ED与 O的位置关系，并说明理由；（2）若 cos MAN= ， AE= ，求阴影部分的面积12 3第 5 页，共 17 页23. 为了美化环境，建设宜居城市，我市准备在一个广场上种植甲、乙两种花卉，经市场调查，甲种花卉的种植费用 y（元）与种植面积 x（ m2）之间的函数关系如图所示，乙种花卉的种植费用为每平方米 100元（1）试求出 y与 x的函数关系式；（2）广场上
9、甲、乙两种花卉的种植面积共 1200m2，若甲种花卉的种植面积不少于200m2，且不超过乙种花卉的种植面积的 2倍试求种植总费用 W元与种植面积 x（ m2）之间的函数关系式；应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用 W最少？最少总费用为多少元？24. 【提出问题】（1）如图 1，在等边 ABC中，点 M是 BC上的任意一点（不含端点 B、 C），连结 AM，以 AM为边作等边 AMN，连结 CN求证： ABC= ACN【类比探究】（2）如图 2，在等边 ABC中，点 M是 BC延长线上的任意一点（不含端点 C），其它条件不变，（1）中结论 ABC= ACN还成立吗？请说明理由【拓
10、展延伸】（3）如图 3，在等腰 ABC中， BA=BC，点 M是 BC上的任意一点（不含端点第 6 页，共 17 页B、 C），连结 AM，以 AM为边作等腰 AMN，使顶角 AMN= ABC连结 CN试探究 ABC与 ACN的数量关系，并说明理由25. 如图，已知抛物线 y=ax2+bx+c（ a0）的顶点坐标为 Q（2，-1），且与 y轴交于点 C（0，3），与 x轴交于 A， B两点（点 A在点 B的右侧），点 P是该抛物线上的一动点，从点 C沿抛物线向点 A运动（点 P与 A不重合），过点 P作 PD y轴，交 AC于点 D（1）求该抛物线的函数关系式；（2）当 ADP是直角三角形时，
11、求点 P的坐标；（3）在题（2）的结论下，若点 E在 x轴上，点 F在抛物线上，问是否存在以 A、 P、 E、 F为顶点的平行四边形？若存在，求点 F的坐标；若不存在，请说明理由第 7 页，共 17 页答案和解析1.【答案】 D【解析】解：-9 的相反数是 9 故选：D根据只有符号不同的两个数互为相反数解答本题考查了互为相反数的定义，是基础题，熟记概念是解题的关键2.【答案】 A【解析】解：将 150 000 000用科学记数法表示为：1.510 8 故选：A科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n的值时，要看把原数变成 a时，小数点移动了多少位，n 的绝
12、对值与小数点移动的位数相同当原数绝对值1 时，n 是非负数；当原数的绝对值1 时，n 是负数此题考查了科学记数法的表示方法科学记数法的表示形式为 a10n的形式，其中1|a|10，n 为整数，表示时关键要正确确定 a的值以及 n的值3.【答案】 D【解析】解：A、4x+5y=4x+5y，错误； B、（-m） 3m7=-m10，错误； C、（x 3y） 5=x15y5，错误； D、a 12a8=a4，正确； 故选：D各式计算得到结果，即可作出判断此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键4.【答案】 B【解析】解：3 是ADG 的外角，3=A+1=30+25=55，l 1l 2，3
13、=4=55，4+EFC=90，EFC=90-55=35，2=35故选：B先根据三角形外角的性质求出3 的度数，再由平行线的性质得出4 的度数，由直角三角形的性质即可得出结论本题考查的是平行线的性质及三角形外角的性质，用到的知识点为：两直线平行，同位角相等5.【答案】 C【解析】解：根据俯视图的特征，应选 C 故选：C注意几何体的特征，主视图与左视图的高相同，主视图与俯视图的长相等，左视图与俯视图的宽相同本题考查了几何体的三视图，正确理解主视图与左视图以及俯视图的特征是解题的关键第 8 页，共 17 页6.【答案】 A【解析】解： ，由得，x1；由得，x2，故此不等式组的解集为：1x2故选：A分
14、别求出各不等式的解集，再求出其公共解集即可本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键7.【答案】 B【解析】解：A、是轴对称图形，不是中心对称图形，不符合题意； B、是轴对称图形，也是中心对称图形，符合题意； C、bu 是轴对称图形，是中心对称图形，不符合题意； D、不是轴对称图形，是中心对称图形，不符合题意 故选：B根据轴对称图形与中心对称图形的概念求解考查了中心对称图形及轴对称图形的知识，掌握中心对称图形与轴对称图形的概念，解答时要注意： 判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合； 判断中心对称图形是
15、要寻找对称中心，图形旋转 180度后与原图重合8.【答案】 C【解析】解：B=70，C=30， BAC=180-100=80， 由作图可知：MN 垂直平分线段 AC， DA=DC， DAC=C=30， BAD=80-30=50， 故选：C根据BAD=BAC-DAC，想办法求出BAC，DAC 即可解决问题本题考查作图-基本作图，线段的垂直平分线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型9.【答案】 A【解析】解：a=-10，二次函数图象开口向下，又对称轴是直线 x=1，当 x1 时，函数图象在对称轴的左边，y 随 x的增大增大故选：A抛物线 y=-x2+2x+1中的对称
16、轴是直线 x=1，开口向下，x1 时，y 随 x的增大而增大本题考查了二次函数 y=ax2+bx+c（a0）的性质：当 a0，抛物线开口向下，对称轴为直线 x=- ，在对称轴左边，y 随 x的增大而增大10.【答案】 C【解析】第 9 页，共 17 页解：O 的直径 CD过弦 EF的中点 G，DCF=20， 弧 DF=弧 DE，且弧的度数是 40， DOE=40， 故选：C根据垂径定理得出弧 DF=弧 DE，求出弧 DE的度数，即可求出答案本题考查了圆周角定理，垂径定理的应用，注意：圆心角的度数等于它所对的弧的度数11.【答案】532【解析】解：原式=3 - = 故答案为： 先将二次根式化为最
17、简，然后合并即可得出答案本题考查了二次根式的加减运算，属于基础题，关键是掌握二次根式的化简及同类二次根式的合并12.【答案】36【解析】解：设甲原有 x文钱，乙原有 y文钱，依题意，得： ，解得： 故答案为：36设甲原有 x文钱，乙原有 y文钱，根据“如果甲得到乙所有钱的一半，那么甲共有 48文；如果乙得到甲所有钱的 ，那么乙共有钱 48文”，即可得出关于 x，y 的二元一次方程组，解之即可得出结论本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键13.【答案】14【解析】解：用 A、B 表示：枣阳汉城、襄阳唐城；画树状图得：一共有 8种可能，则三家投到同一景点游
18、玩的有 2种情况，故三家投到同一景点游玩的概率是： = 第 10 页，共 17 页故答案为： 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与三家抽到同一景点的情况，再利用概率公式求解即可求得答案本题考查的是用列表法或画树状图法求概率注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件注意概率=所求情况数与总情况数之比14.【答案】四【解析】解：在一次函数 y=kx+2中，y 随 x的增大而增大， k0， 20， 此函数的图象经过一、二、三象限，不经过第四象限 故答案为：四先根据函数的增减性判断出 k的符号，再根
19、据一次函数的图象与系数的关系进行解答即可本题考查的是一次函数的图象与系数的关系，即一次函数 y=kx+b（k0）中，当k0，b0 时，函数的图象经过一、二、三象限15.【答案】2.4 cm或 cm2411【解析】解：如图 AB=AC=8cm，BC=6cm，设平行四边形的短边为 xcm，若 BE是平行四边形的一个短边，则 EFAB，= ，解得 x=2.4厘米，若 BD是平行四边形的一个短边，则 EFAB，= ，解得 x= ，综上所述短边为 2.4cm或 cm设平行四边形的短边为 xcm，分两种情况进行讨论，若 BE是平行四边形的一个短边，若 BD是平行四边形的一个短边，利用三角形相似的性质求出
20、x的值本题主要考查相似三角形的判定与性质等知识点，解答本题的关键是正确的画出图形，结合图形很容易解答16.【答案】134【解析】解：过 Q点作 QGCD，垂足为 G点，连接 QE，设 PQ=x，由折叠及矩形的性质可知，EQ=PQ=x，QG=PD=3，EG=x-2，在 RtEGQ 中，由勾股定理得EG2+GQ2=EQ2，即：（x-2） 2+32=x2，第 11 页，共 17 页解得：x= ，即 PQ= 过 Q点作 QGCD，垂足为 G点，连接 QE，设 PQ=x，根据折叠及矩形的性质，用含 x的式子表示 RtEGQ 的三边，再用勾股定理列方程求 x即可本题考查图形的翻折变换，解题过程中应注意折叠
21、是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应线段相等17.【答案】解：（ - ）2+ 2+=(2)()(+)(+)() +2=223+22 12=2(2) 12= ，2当 a= + ， b= - 时，2 3 2 3原式= = = 2(2+3)(2+3)(23)2(2+3)23 6+33【解析】根据分式的减法和除法可以化简题目中的式子，然后将 a、b 的值代入化简后的式子即可解答本题本题考查分式的化简求值、分母有理化，解答本题的关键是明确分式化简求值的计算方法18.【答案】94 95.5 93 95.5【解析】解：（1）九（1）班的平均分=
22、=94，九（2）班的中位数为（96+95）2=95.5，九（2）班的众数为 93，故答案为：94 95.5 93；（2）九（2）班平均分高于九（1）班；九（2）班的成绩集中在中上游；九（2）班的成绩比九（1）班稳定；故支持 B班成绩好；（3）如果九（2）班有一半的学生评定为“优秀”等级，标准成绩应定为 95.5（中位数）因为从样本情况看，成绩在 95.5以上的在九（2）班有一半的学生可以估计，如果标准成绩定为 95.5，九（2）班有一半的学生能够评定为“优秀”等级，故答案为 95.5（1）求出九（1）班的平均分确定出 m的值，求出九（2）班的中位数确定出 n的值，求出九（2）班的众数确定出 p
23、的值即可；（2）分别从平均分，方差，以及中位数方面考虑，写出支持九（2）班成绩好的原因；（3）用中位数作为一个标准即可衡量是否有一半学生达到优秀等级本题考查了平均数、中位数、众数以及方差的定义，属于统计中的基本题型，需重点掌握第 12 页，共 17 页19.【答案】解：设每件降价 a元，总利润为 w，则（60-40- a）（300+20 a）=6000 整理，得-20 a2+100a+6000=6000 解得 a1=0（舍去）， a2=5所以定价为 65元/件时，每天的利润达到 6000元答：定价为 65元/件时，每天的利润达到 6000元【解析】设每件降价 a元，则每件的利润是（60-40-
24、a）元，所售件数是（300+20a）件，根据利润=每件的利润所售的件数，列出方程并解答考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解20.【答案】解：设 CD=x米在 Rt ACD中， ，37=则 ，34= ；=34在 Rt BCD中，tan48= ，则 ，1110= （4 分）=1110 AD+BD=AB， ，34+1110=80解得： x43答：小明家所在居民楼与大厦的距离 CD大约是 43米（6 分）【解析】利用所给角的三角函数用 CD表示出 AD、BD；根据 AB=AD+BD=80米，即可求得居民楼与大厦的距离本题考查直角
25、三角形的解法，首先构造直角三角形，再运用三角函数的定义解题21.【答案】解：（1）一次函数y1=k1x+1的图象与 y轴交于点 A，与 x轴交于点 B， A（0，1）， B（- ，0）11 AOB的面积为 1， OBOA=1，12（- ）1=1，12 11第 13 页，共 17 页 k1=- ，12一次函数的解析式为 y1=- x+1；12当 y=2时，- x+1=2，解得 x=-2，12 M的坐标为（-2，2）点 M在反比例函数的图象上， k2=-22=-4，反比例函数的解析式为 y2=- ；4（2）解方程组 ，=12+1=4 得 或 ，=2=2 =4=1故当 y1 y2时， x-2 或 0
26、 x4【解析】（1）先由一次函数的解析式为 y1=k1x+1，求出点 A与点 B的坐标，再根据AOB 的面积为 1，可得到 k1的值，从而求出一次函数的解析式；进而得到点 M的坐标，然后运用待定系数法即可求出反比例函数的解析式； （2）y 1y 2即一次函数值大于反比例函数值，只需观察一次函数的图象落在反比例函数的图象的上方时自变量的取值范围即可，为此，先求出它们的交点坐标，再根据函数图象，可知在点 M的左边以及原点和点 N之间的区间，y 1y 2本题考查了反比例函数和一次函数的交点问题，以及用待定系数法求反比例函数和一次函数的解析式，是基础知识要熟练掌握22.【答案】解：（1） DE与 O相
27、切理由如下：连接 OE， AE平分 MAN，1=2 OA=OE，2=31=3 OE AD OEF= ADF=90 OE DE，垂足为 E点 E在半圆 O上， ED与 O相切（2）cos MAN= ，12 MAN=602= MAN= 60=3012 12 AFD=90- MAN=90-60=30第 14 页，共 17 页2= AFD EF=AE= 3在 Rt OEF中，tan OFE= ，tan30= 3 OE=14= MAN=60， S 阴 =S OEF-S 扇形 OEB= = 121360123603216【解析】（1）连接 OE，根据角平分线的性质及等边对等角可求得1=3，再根据平行线的性
28、质即可得到 OEDE，因为 OE是半径，从而得到 ED与O 相切 （2）由已知可得到MAN=60，从而推出2=AFD=30，根据等角对等边得到EF=AE，再根据 S 阴 =SOEF -S 扇形 OEB即可求解此题主要考查学生对切线的判定方法及扇形面积计算的综合运用能力23.【答案】解：（1）当 0 x300 时，设 y=k1x，根据题意得 300k1=39000，解得k1=130，即 y=130x；当 x300 时，设 y=k2x+b，根据题意得 ，解得 ，即3002=390005002=55000 2=80=15000y=80x+15000， y= ；130(0130)80+15000(30
29、0)（2）当 200 x300 时， w=130x+100（1200- x）=30 x+120000；当 x300 时， w=80x+15000+100（1200- x）=-20 x+135000；设甲种花卉种植为 am2，则乙种花卉种植（1200- a） m2， ，2002(1200)200 a800当 a=200 时 Wmin=126000 元当 a=800时， Wmin=119000 元119000126000当 a=800时，总费用最少，最少总费用为 119000元此时乙种花卉种植面积为 1200-800=400m2答：应该分配甲、乙两种花卉的种植面积分别是 800m2和 400m2，
30、才能使种植总费用最少，最少总费用为 119000元【解析】（1）由图可知 y与 x的函数关系式是分段函数，待定系数法求解析式即可 （2）根据（1）的结论解答即可； 设甲种花卉种植为 am 2，则乙种花卉种植（1200-a）m 2，根据实际意义可以确定 a的范围，结合种植费用 w（元）与种植面积 a（m 2）之间的函数关系可以分类讨论最少费用为多少本题是看图写函数解析式并利用解析式的题目，考查分段函数的表达式和分类讨论的数学思想第 15 页，共 17 页24.【答案】（1）证明： ABC、 AMN是等边三角形， AB=AC， AM=AN， BAC= MAN=60， BAM= CAN，在 BAM和
31、 CAN中， BAM CAN（ SAS）， = ABC= ACN（2）解：结论 ABC= ACN仍成立；理由如下： ABC、 AMN是等边三角形， AB=AC， AM=AN， BAC= MAN=60， BAM= CAN，在 BAM和 CAN中， BAM CAN（ SAS）， = ABC= ACN（3）解： ABC= ACN；理由如下： BA=BC， MA=MN，顶角 ABC= AMN，底角 BAC= MAN， ABC AMN， = ，又 BAM= BAC- MAC， CAN= MAN- MAC， BAM= CAN， BAM CAN， ABC= ACN【解析】（1）利用 SAS可证明BAMCAN
32、，继而得出结论；（2）也可以通过证明BAMCAN，得出结论，和（1）的思路完全一样（3）首先得出BAC=MAN，从而判定ABCAMN，得到 = ，根据BAM=BAC-MAC，CAN=MAN-MAC，得到BAM=CAN，从而判定BAMCAN，得出结论本题考查了相似三角形的判定与性质、全等三角形的判定与性质，解答本题的关键是仔细观察图形，找到全等（相似）的条件，利用全等（相似）的性质证明结论25.【答案】解：（1）抛物线的顶点为 Q（2，-1），设抛物线的解析式为 y=a（ x-2） 2-1，将 C（0，3）代入上式，得：3=a（0-2） 2-1， a=1； y=（ x-2） 2-1，即 y=x2
33、-4x+3；（2）分两种情况：当点 P1为直角顶点时，点 P1与点 B重合；令 y=0，得 x2-4x+3=0，解得 x1=1， x2=3；第 16 页，共 17 页点 A在点 B的右边， B（1，0）， A（3，0）； P1（1，0）；当点 A为 AP2D2的直角顶点时； OA=OC， AOC=90， OAD2=45；当 D2AP2=90时， OAP2=45， AO平分 D2AP2；又 P2D2 y轴， P2D2 AO， P2、 D2关于 x轴对称；设直线 AC的函数关系式为 y=kx+b（ k0）将 A（3，0）， C（0，3）代入上式得：，3+=0=3解得 ；=1=3 y=-x+3；设
34、D2（ x，- x+3）， P2（ x， x2-4x+3），则有：（- x+3）+（ x2-4x+3）=0，即 x2-5x+6=0；解得 x1=2， x2=3（舍去）；当 x=2时， y=x2-4x+3=22-42+3=-1； P2的坐标为 P2（2，-1）（即为抛物线顶点） P点坐标为 P1（1，0）， P2（2，-1）；（3）由（2）知，当 P点的坐标为 P1（1，0）时，不能构成平行四边形；当点 P的坐标为 P2（2，-1）（即顶点 Q）时，平移直线 AP交 x轴于点 E，交抛物线于 F； P（2，-1），可设 F（ x，1）； x2-4x+3=1，解得 x1=2- ， x2=2+ ；2
35、 2符合条件的 F点有两个，即 F1（2- ，1）， F2（2+ ，1）2 2【解析】（1）已知了抛物线的顶点坐标，可将抛物线的解析式设为顶点式，然后将函数图象经过的 C点坐标代入上式中，即可求出抛物线的解析式； （2）由于 PDy 轴，所以ADP90，若ADP 是直角三角形，可考虑两种情况： 以点 P为直角顶点，此时 APDP，此时 P点位于 x轴上（即与 B点重合），由此可求出 P点的坐标； 以点 A为直角顶点，易知 OA=OC，则OAC=45，所以 OA平分CAP，那么此时D、P 关于 x轴对称，可求出直线 AC的解析式，然后设 D、P 的横坐标，根据抛物线和直线 AC的解析式表示出 D、P 的纵坐标，由于两点关于 x轴对称，则纵坐标互为相反数，可据此求出 P点的坐标； （3）P、B 重合，E 点在 x轴上，这样 A、P、E 三点在 x轴上，所以 A、P、E、F 为顶第 17 页，共 17 页点不可能构成平行四边形，所以只有（2）的一种情况符合题意，由知此时 P、Q重合；假设存在符合条件的平行四边形，那么根据平行四边形的性质知：P、F 的纵坐标互为相反数，可据此求出 F点的纵坐标，代入抛物线的解析式中即可求出 F点的坐标此题主要考查了二次函数解析式的确定、直角三角形的判定、平行四边形的判定和性质等重要知识点，同时还考查了分类讨论的数学思想，能力要求较高，难度较大
