1、2019年中考数学压轴题专项训练：一次函数综合1已知， A（0，8） ， B（4，0） ，直线 y x沿 x轴作平移运动，平移时交 OA于 D，交 OB于 C（1）当直线 y x从点 O出发以 1单位长度/ s的速度匀速沿 x轴正方向平移，平移到达点 B时结束运动，过点 D作 DE y轴交 AB于点 E，连接 CE，设运动时间为 t（ s） 是否存在 t值，使得 CDE是以 CD为腰的等腰三角形？如果能，请直接写出相应的 t值；如果不能，请说明理由将 CDE沿 DE翻折后得到 FDE，设 EDF与 ADE重叠部分的面积为 y（单位长度的平方） 求 y关于 t的函数关系式及相应的 t的取值范围；
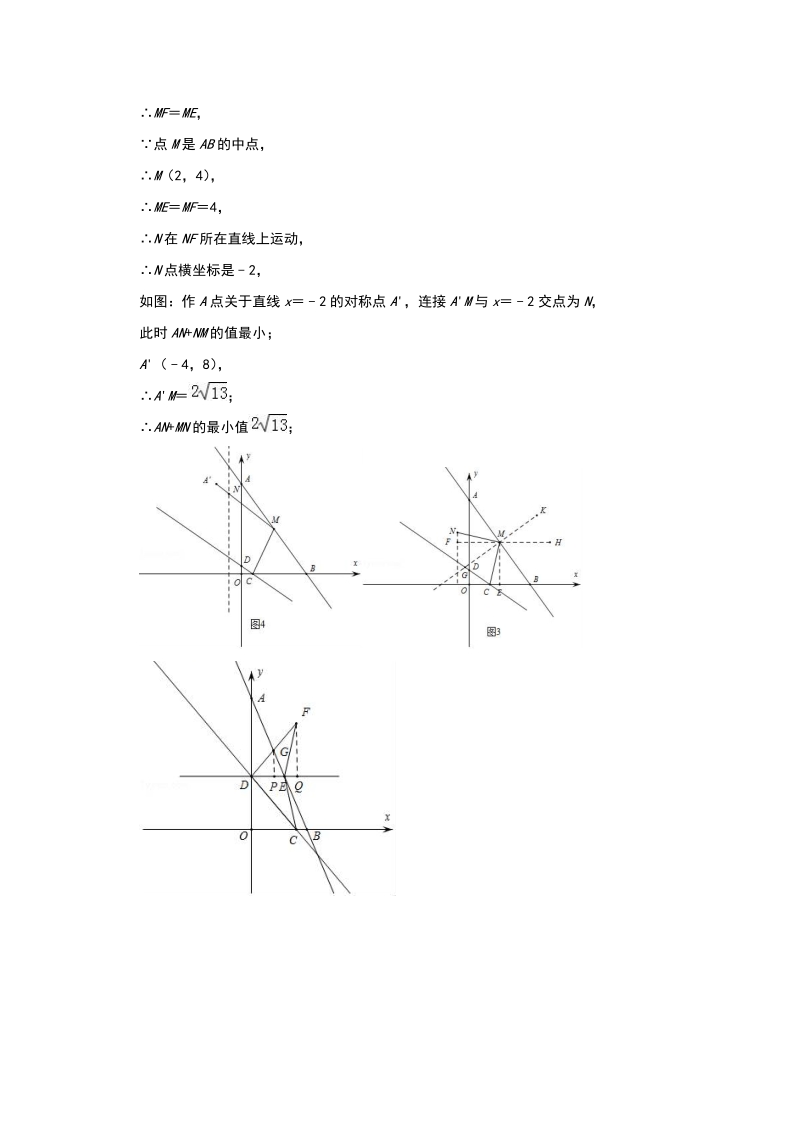
2、（2）若点 M是 AB的中点，将 MC绕点 M顺时针旋转 90得到 MN，连接 AN，请直接写出AN+MN的最小值解：（1）设过 A（0，8） ， B（4，0）两点的直线解析式为 y kx+b， y2 x+8，直线 y x从点 0出发以 1单位长度/ s的速度匀速沿 x轴正方向平移，此时函数解析式为 y x+t， D（0， t） ， E（82 t， t） ， C（ t，0） ，当 CD CE时，2 t2（83 t） 2+t2， t2 或 t4，当 CD DE时，DE|82 t|， CD t，|82 t| t， t4 +8，或 t8+4 ，0 t3， t2 或 t4 +8； CDE沿 DE翻折后
3、得到 FDE， F（ t，2 t） ，当 F在直线 AB上时， t2，0 t2 时，y S EFD （82 t） t t2+4t，当 2 t4 时，DF所在直线解析式为 y x+t， DF AB，作 GP DE， FQ DE， FQ t， DQ t， GP2 PE， DE82 t， ， GP ，y （82 t） t2 t+ ；（3）如图 3：过点 M作 ME x轴，交 x轴于 E点；过点 M作 y轴垂线，过 N做 x轴垂线，相交于点 F；过点 M做 AB直线的垂线， NMC NMG+ CMG90， GMB GMC+ CMB90， NMG CMB， FH x轴， CBA HMB， FMG KMH
4、， KMH+ HMB90， BME+ MBE90， BME KMH FMG， CM E NMF，在 Rt NMF和 Rt CME中， MN MC， CME NMF，Rt NMF和 Rt CME（ AAS） ， MF ME，点 M是 AB的中点， M（2，4） ， ME MF4， N在 NF所在直线上运动， N点横坐标是2，如图：作 A点关于直线 x2 的对称点 A，连接 AM与 x2 交点为 N，此时 AN+NM的值最小；A（4，8） ， AM ； AN+MN的最小值 ；2如图， A、 B分别是 x轴上位于原点左右两侧的点，点 P（2， p ）在第一象限，直线 PA交 y轴于点 C（0，2）
5、，直线 PB交 y轴于点 D， AOP的面积为 6（1）求点 A的坐标；（2）求点 P的坐标；（3）若 BOP是以 OP为腰的等腰三角形，直接写出直线点 D坐标解：（1）作 PE y轴于 E， P的横坐标是 2，则 PE2 S COP OCPE 222； S AOC S AOP S COP624， S AOC OAOC4，即 OA24， OA4， A的坐标是（4，0） （2）设直线 AP的解析式是 y kx+b，则，解得： ，则直线的解析式是 y x+2当 x2 时， y3，即 p3，点 P的坐标为（2，3） ；（3）当 OP PB时，作 PF x轴于 F， F（2，0） ， F是线段 OB的
6、中点， B（4，0） ，直线 BP： y x+6， D（0，6） ；当 OP OB时， OP ， B（ ，0） ，直线 BP： y x+ ， D（0， ） 3一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，匀速行驶，设慢车行驶的时间 x（ h） ，两车之间的距离为 y（ km） ，图中的折线表示 y与 x之间的函数关系根据图象回答：（1）甲、乙两地之间的距离为 900 km ；（2）两车同时出发后 4 h相遇；（3）慢车的速度为 75 千米/小时；快车的速度为 150 千米/小时；（4）线段 CD表示的实际意义是 快车到达乙地后，慢车继续行驶到甲地 解：（1）由图象可得，甲、乙两
7、地之间的距离为 900km，故答案为：900 km；（2）由图象可得，两车同时出发后 4h相遇，故答案为：4；（3）慢车的速度为：9001275 km/h，快车的速度为：900475150 km/h，故答案为：75，150；（4）线段 CD表示的实际意义是快车到达乙地后，慢车继续行驶到甲地，故答案为：快车到达乙地后，慢车继续行驶到甲地4如图，在平面直角坐标系 xOy中，过点 A（6，0）的直线 l1与直线 l2： y2 x相交于点 B（ m，6）（1）求直线 l1的表达式（2）直线 l1与 y轴交于点 M，求 BOM的面积；（3）过动点 P（ m，0）且垂于 x轴的直线与 l1， l2的交点分
8、别为 C， D，当点 C位于点D下方时，写出 n的取值范围解：（1）将点 B（ m，6）代入 y2 x， m3， B（3，6） ；设直线 l1的表达式为 y kx+b，将点 A与 B代入，得， ， y x+4；（2） M（0，4） ， S BOM 436；（3） 当点 C位于点 D下方时，即 y1 y2， m3；5麒麟区有甲、乙两家草莓采摘园的草莓销售价格相同， “春节期间” ，两家采摘园将推岀优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的草莓六折优惠：乙园的优惠方案是：游客进园不需购买门票，采摘园的草莓按售价付款，优惠期间，设游客的草莓采摘量为 x（千克） ，在甲园所需总费用为 y
9、甲 （元） ，在乙园所需总费用为 y 乙 元， y甲 、 y 乙 与 x之间的函数关系如图所示（1）求 y 甲 、 y 乙 与 x的函数表达式；（2）在春节期间，李华一家三口准备去草莓园采摘草莓，采摘的草莓合在一起支付费用，则李华一家应选择哪家草莓园更划算？解：（1）3001030（元/千克）根据题意得 y 甲 18 x+60，设 y 乙 k2x，根据题意得，10k2300，解答 k230， y 乙 30 x；（2）当 y 甲 y 乙 ，即 18x+6030 x，解得 x5，所以当采摘量大于 5千克时，到家草莓采摘园更划算；当 y 甲 y 乙 ，即 18x+6030 x，解得 x5，所以当采摘
10、量为 5千克时，到两家草莓采摘园所需总费用一样；当 y 甲 y 乙 ，即、18 x+6030 x，解得 x5，所以当采摘量小于 5克时，到家乙莓采摘园更划算6甲、乙两人在笔直的道路 AB上相向而行，甲骑自行车从 A地到 B地，乙驾车从 B地到A地，假设他们分别以不同的速度匀速行驶，甲先出发 6分钟后，乙才出发，乙的速度为 千米/分，在整个过程中，甲、乙两人之间的距离 y（千米）与甲出发的时间 x（分）之间的部分函数图象如图（1） A、 B两地相距 24 千米，甲的速度为 千米/分；（2）求线段 EF所表示的 y与 x之间的函数表达式；（3）当乙到达终点 A时，甲还需多少分钟到达终点 B？解：（
11、1）观察图象知 A、 B两地相距为 24km，甲先行驶了 2千米，由横坐标看出甲行驶 2千米用了 6分钟，甲的速度是 千米/分钟；故答案为：24， ；（2）设甲乙需要时时间为 a分钟，根据题意得，解答 a18， F（18，0） ，设线段 EF表示的 y与 x之间的函数表达式为 y kx+b，根据题意得，解得 ，线段 EF表示的 y与 x之间的函数表达式为 y x+33；（3）相遇后乙到达 A地还需：（18 ） 4（分钟） ，相遇后甲到达 B站还需：（12 ） 54（分钟）当乙到达终点 A时，甲还需 54450 分钟到达终点 B7如图 1，在平面直角坐标系中，一次函数 y x+8的图象与 y轴交
12、于点 A，与 x轴交于点 B，点 C是 x轴正半轴上的一点，以 OA， OC为边作矩形 AOCD，直线 AB交 OD于点E，交直线 DC于点 F（1）如图 2，若四边形 AOCD是正方形求证： AOE COE；过点 C作 CG CE，交直线 AB于点 G求证： CG FG（2）是否存在点 C，使得 CEF是等腰三角形？若存在，求该三角形的腰长；若不存在，请说明理由解：（1）四边形 AOCD是正方形 AO CO， AOD EOC， AOE COE（ SAS） ； AOE COE， OAB ECB， OAB+ OBA OAB+ CBG90， ECB+ CBG90， CG CE， CBG BCG，
13、BG CG，在 Rt BCF中， BCG+ FCG90， CBG+ CFB90， GCF CFG， CG GF；（2）设 C（ m，0） ， F（ m， m+8） ， D（ m，8） ，直线 OD的解析式为 y x，两直线 y x与 y x+8的交点为 E，x x+8， x ， E（ ， ） ， EC2 ， CF2 ， EF2 ，当 EC EF时， ， m ；当 CF EF时， ， m4；当 EC EF时， ， m6；此时 C与 F重合，不合题意；综上所述： m4 或 m 时 CEF是等腰三角形；8如图，在平面直角坐标系中，点 O为坐标原点，点 A在 y轴的正半轴上，点 B在 x轴的负半轴上，
14、点 C是线段 AB上一动点 CD y轴于点 D， CE x轴于点 E， OA6， AD OE（1）求直线 AB的解析式；（2）连接 ED，过点 C作 CF ED，垂足为 F，过点 B作 x轴的垂线交 FC的延长线于点G，求点 G的坐标；（3）在（ 2）的条件下，连接 AG，作四边形 AOBG关于 y轴的对称图形四边形 AONM，连接 DN，将线段 DN绕点 N逆时针旋转 90得到线段 PN， H为 OD中点，连接 MH、 PH，四边形 MHPN的面积为 40，连接 FH，求线段 FH的长解：（1） CD y轴， CE x轴 CDO CEO90又 DOE90四边形 DCEO是矩形 CD OE又
15、AD OE AD CE AD CD ACD是等腰直角三角形 ACD45 ABO45 ACD ABO AO BO6 A（0，6） ， B（6，0）设直线 AB的解析式为 y kx+6将 A（6，0）代入，得 06 k+6解得， k1直线 AB的解析式为： y x+6（2）如图所示，设 D（0， a） ，则 OD CE a， AD CD EO6 a C（ a6， a） ， E（ a6，0）设 yDE k1x+a，将 E（ a6，0）代入，得，0（ a6） k1+a解得， yDE设 yFG k2x+b1 DE FG k1k21 yFG将 C（ a6， a）代入， 得，解得， yFG当 x6 时， y
16、FG6 G点坐标为（6，6）（3）根据题意，如图所示可证 ODN NPK ON NK6四边形 ONKL为正方形设 AD a，则 OH DH3PK OD6 aLP aSMHPN SAMKL S AMH S NKP S OLP612 453 a+453 a+ 40解得 a12， a210（舍）作 FS CD可得 CD2， EC4 ED2由等面积法CDCE EDCF24 CF CF CD2 DFCDFS CFFDFS SD F（ ， ） FH9对于平面直角坐标系 xOy中的直线 l和图形 M，给出如下定义：P1、 P2、 Pn1 、 Pn是图形 M上 n（ n3）个不同的点，记这些点到直线 l的距离
17、分别为 d1、 d2、 dn1 、 dn，若这 n个点满足 d1+d2+dn1 dn，则称这 n个点为图形 M关于直线 l的一个基准点列，其中 dn为该基准点列的基准距离（1）当直线 l是 x轴，图形 M上有三点 A（1，1） 、 B（1，1） 、 C（0，2）时，判断A、 B、 C是否为图形 M关于直线 l的一个基准点列？如果是，求出它的基准距离；如果不是，请说明理由；（2）已知直线 l是函数 y x+3的图象，图形 M是圆心在 y轴上，半径为 1的 T， P1、 P2、 Pn1 、 Pn是 T关于直线 l的一个基准点列若 T为原点，求该基准点列的基准距离 dn的最大值；若 n的最大值等于
18、6，直接写出圆心 T的纵坐标 t的取值范围解：（1） A、 B、 C是图形 M关于直线 l的一个基准点列， A（1，1） ， B（0，2） ， C（1，1）到 x轴的距离分别是 1，1，2，且 1+12，这三点为图形 M关于直线 l的一个基准点列，它的基准距离为 2；（2） P1、 P2、 Pn1 、 Pn是 T关于直线 l的一个基准点列， d1+d2+dn1 dn， dn的最大值为 T上的点到直线 l的最大距离，当 T为原点时，过 P作 OH l，垂足为 H，延长 HO交 O于点 F，则 FH的长度为 dn的最大值，设函数： y 的图象与 x轴， y轴分别交于点 D， E，则 D（ ，0）
19、， E（0，3） ， OD ， OE3， DOE90， OED30， OHE90， OH OE1.5， FH2.5，显然， O上存在点 P1、 P2、 P3、 P4满足 ， dn的最大值为 2.5；当 n6 时， d1+d2+d3+d4+d5 d6，当 t0 时， FH2.5， PH0.5，2.50.55， t0 时， n的最大值为 5，易知当 t0 时， n的最大值会小于 5，当 t0 时， n的最大值大于 5，设当圆心沿 y轴正方向移动到点 M时， n的最大值恰好为 6，设 MH与圆交于点 G，则， GH ， MH ， ， ME ， OM ，0 t 符合题意；同理在点 E上方距离点 E 的
20、位置为符合条件地临界位置，故符合题意综上，圆心 T的纵坐标 t的取值范围为 0 t 或 10已知一个矩形纸片 OACB，将该纸片放置在平面直角坐标系中，点 A（4，0） ，点B（0，3） ，点 P为 BC边上的动点（点 P不与点 B、 C重合） ，经过点 O、 P折叠该纸片，得点 B和折痕 OP设 BP t（1）如图 1，当 BOP30时，求点 P的坐标；（2）如图 2，经过点 P再次折叠纸片，使点 C落在直线 PB上，得点 C和折痕 PQ，设 AQ m，试用含有 t的式子表示 m；（3）在（2）的条件下，连接 OQ，当 OQ取得最小值时，求点 Q的坐标；（4）在（2）的条件下，点 C能否落在
21、边 OA上？如果能，直接写出点 P的坐标；如果不能，请说明理由解：（1） A（4，0） ， B（0，3） ， OA4， OB3，在 Rt OBP中， BOP30， PB ，点 P的坐标为（ ，3） ，（2）由题意，得 BP t， PC4 t， CQ3 m，由折叠可知： OPB OPB， CPQ C PQ，又 OPB+ OPB+ CPQ+ C PQ180， OPB+ CPQ90，又 OPB+ BOP90， OPB CPQ，又 OBP C90， OBP PCQ， ， ， m t2 t+3；（3） OQ2 OA2+A Q24 2+AQ216+ AQ2，当 AQ最短时， OQ最短， AQ m t2 t
22、+3 （ t2） 2+ ，当 t2 时， AQ最短， OQ最短，此时点 Q（4， ） ，（4）点 C不能落在边 OA上，理由：假设点 C能落在边 OA上，由折叠可得PB PB t， PC PC4 t， OB OB3， OPB OPC， OB P OBP90， BC OA， BPO POC， OPC POC， OC PC4 t， B C PC PB（4 t） t42 t，在 Rt OB C中， B O2+B C 2 OC 2，3 2+（42 t） 2（4 t） 2，整理，得 3t28 t+90，（8） 24390，该方程无实数解，点 C不能落在边 OA上11为增强学生体质，某中学在体育课中加强了
23、学生的长跑训练在一次男子 1000米耐力测试中，小明和小亮同时起跑，同时到达终点；所跑的路程 S（米）与所用的时间t（秒）之间的函数图象如图所示：（1）当 80 t180 时，求小明所跑的路程 S（米）与所用的时间 t（秒）之间的函数表达式；（2）求他们第一次相遇的时间是起跑后的第几秒？解：（1）设当 80 t180 时，小明所跑的路程 S（米）与所用的时间 t（秒）之间的函数表达式为 y1 k1x+b，由题意，得解得：当 80 t180 时，小明所跑的路程 S（米）与所用的时间 t（秒）之间的函数表达式为 y12 x+200，（2）设小亮所跑的路程 S（米）与所用的时间 t（秒）之间的函数表
24、达式为 y kx，代入（250，100 0）得 1000250 k，解得 k4，故小亮所跑的路程 S（米）与所用的时间 t（秒）之间的函数表达式为 y4 x，当 y y1时，4 x2 x+200，解得： x100所以他们第一次相遇的时间是起跑后的第 100秒12如图，在平面直角坐标系中，矩形 OABC的顶点 A在 y轴的正半轴上，点 C在 x轴的正半轴上，线段 OA， OC的长分别是 m， n且满足 ，点 D是线段 OC上一点，将 AOD沿直线 AD翻折，点 O落在矩形对角线 AC上的点 E处（1）求 OA， OC的长；（2）求直线 AD的解析式；（3）点 M在直线 DE上，在 x轴的正半轴上
25、是否存在点 N，使以 M、 A、 N、 C为顶点的四边形是平行四边形？若存在，请直接写出点 N的坐标；若不存在，请说明理由解：（1）线段 OA， OC的长分别是 m， n且满足 ， OA m6， OC n8；（2）设 DE x，由翻折的性质可得： OA AE6， OD DE x， DC8 OD8 x，AC ，可得： EC10 AE1064，在 Rt DEC中，由勾股定理可得： DE2+EC2 DC2，即 x2+42（8 x） 2，解得： x3，可得： DE OD3，所以点 D的坐标为（3，0） ，设 AD的解析式为： y kx+b，把 A（0，6） ， D（3，0）代入解析式可得： ，解得：
26、，所以直线 AD的解析式为： y2 x+6；（3）过 E作 EG OC，在 Rt DEC中， ，即 ，解得： EG2.4，在 Rt DEG中， DG ，所以点 E的坐标为（4.8，2.4） ，设直线 DE的解析式为： y ax+c，把 D（3，0） ， E（4.8，2.4）代入解析式可得： ，解得： ，所以 DE的解析式为： y x4，把 y6 代入 DE的解析式 y x4，可得： x7.5，即 AM7.5，当以 M、 A、 N、 C为顶点的四边形是平行四边形时，CN AM7.5，所以 N8+7.515.5， N87.50.5，即存在点 N，且点 N的坐标为（0.5，0）或（15.5，0） 1
27、3如图 1，直线 11： y x+6与 x轴， y轴分别交于 B， A两点，过点 A做 AC AB交 x轴于点 C，将直线 l1沿着 x轴正方向平移 m个单位得到直线 l2交直线 AC于点 D，交 x轴于点 E，将 CDE沿直线 l2翻折得到点 F（1）若 m2 ，求点 E；（2）若 BCF的面积等于 4 ，求 l2的解析式；（3）在（1）的条件下，将 ABO绕点 C旋转 60得到 A1B1O1，点 R是直线 l2上一点，在直角坐标系中是否存在点 S，使得以点 A1、 B1、 R、 S为顶点的四边形是矩形？若存在，求出点 S的坐标；若不存在，请说明理由解：（1） y x+6与 x轴， y轴分别
28、交于 B， A两点， A（0，6） ， B（2 ，0） ， y x+6向右平移 2 个单位， y （ x2 ）+6 x， E（0，0） ；（2） l2： y （ x m）+6， E（ m2 ，0） ， AC AB，直线 AC的解析式 y x+6， C（6 ，0） ， EC8 m，设 F点的纵坐标为 h，BC8 ， BCF的面积等于 4 ，4 8 h， h1，tan B ， ABO60， BAC30， CF2，在 RtCED中， CD1， CE ， OE ， m ， y x16；（3） ABO绕点 C旋转 60得到 A1B1O1， BCB1， OO1C都是等边三角形， B1（2 ，12） ， O
29、1（3 ，9） ， A1（6 ，12） ，当 B1RSA1是矩形时， B1R B1A1， R在 y x上， R（2 ，6） ；当 B1RA1S是矩形时， B1R RA1， R与 O1重合， R（3 ，9） ；故存在 R使得以点 A1、 B1、 R、 S为顶点的四边形是矩形，R（2 ，6） ， R（3 ，9） ；14慢车和快车先后从甲地出发沿直线道路匀速驶向乙地，快车比慢车晚出发 0.5小时，行驶一段时间后，快车途中体息，休息后继续按原速行驶，到达乙地后停止慢车和快车离甲地的距离 y（千米）与慢车行驶时间 x（小时）之间的函数关系如图所示（1）直接写出快车速度是 120 千米/小时（2）求快车到
30、达乙地比慢车到达乙地早了多少小时？（3）求线段 BC对应的函数关系式解：（1）快车速度是（400280）（4.53.5）120（千米/小时） 故答案为：120；（2）慢车速度是 2803.580（千米/小时） 慢车到达乙地需要的时间是 400805（小时） ，快车到达乙地比慢车到达乙地早了 54.50.5（小时） ；（3）快车比慢车晚出发 0.5小时， B的坐标为（0.5，0） ，快车从甲地驶向乙地需要的时间是 400120 （小时） ；又实际到达时间是慢车出发后 4.5小时，且快车比慢车晚出发 0.5小时，快车途中休息时间是 4.50.5 （小时）2 ， ，点 C的坐标为（ ，100） ，设
31、 BC的解析式为： y kx+b，把 B（0.5，0）和 C（ ，100）代入解析式可得： ，解得： ，所以 BC的解析式为： y120 x6015如图 1，已知在平面直角坐标系中，点 O为坐标原点，点 A在 x轴负半轴上，直线y x+6与 x轴、 y轴分别交于 B、 C两点，四边形 ABCD为平行四边形，且 AC BC，点P为 ACD内一点，连接 AP、 BP且 APB90（1）求证： PAC PBC；（2）如图 2，点 E在线段 BP上，点 F在线段 AP上，且 AF BE， AEF45，求EF2+2AE2的值；（3）在（2）的条件下，当 PE BE时，求点 P的坐标解：（1）当 x0 时
32、， y6；当 y0 时， x6， B（6，0） ； C（0，6） ， BOC为等腰直角三角形，又 AC BC， ACB为等腰直角三角形，又 APB90，设 AC与 BP相交于点 G，则在 Rt APG中， PAC+ PGA90同理，在 Rt ACB中， PBC+ BGC90而 PGA BGC， PAC PBC；（2）连接 CE、 CF，在 AFC和 BEC中， AF BE， PAC PBC， AC BC， AFC BEC（ SAS） ， CE CF， ACF BCE， FCE ACF+ ACE BCE+ ACE ACB90， CEF为等腰直角三角形， CEF45， ，又 AEF45， AEC
33、CEF+ AEF90，在 Rt AEC中 CE2+AE2 AC2， ， ，（3）设 AF BE PE m， PF n，在 Rt PEF中， EF2 m2+n2，在 Rt PEA中， AE2（ m+n） 2+m2，由（2）得： ，（ m2+n2）+2（ m+n） 2+m2）144，整理得：2（ m+n） 2+3m2+n2144，在 Rt PBA中， PA2+PB2 AB2，即（ m+n） 2+（2 m） 212 2，整理得（ m+n） 2+4m2144，由得：（ m+n） 2+n2 m202 n（ m+n）0， m+n0， n0，即点 P、 F重合时恰有 PE BE，在 Rt PAB中， AP： BP： AB ，又 AB12， AP ，过 P作 PQ AB于点 Q，则 PAQ BAP， AQ： PQ： AP ， ， P（ ， ）
