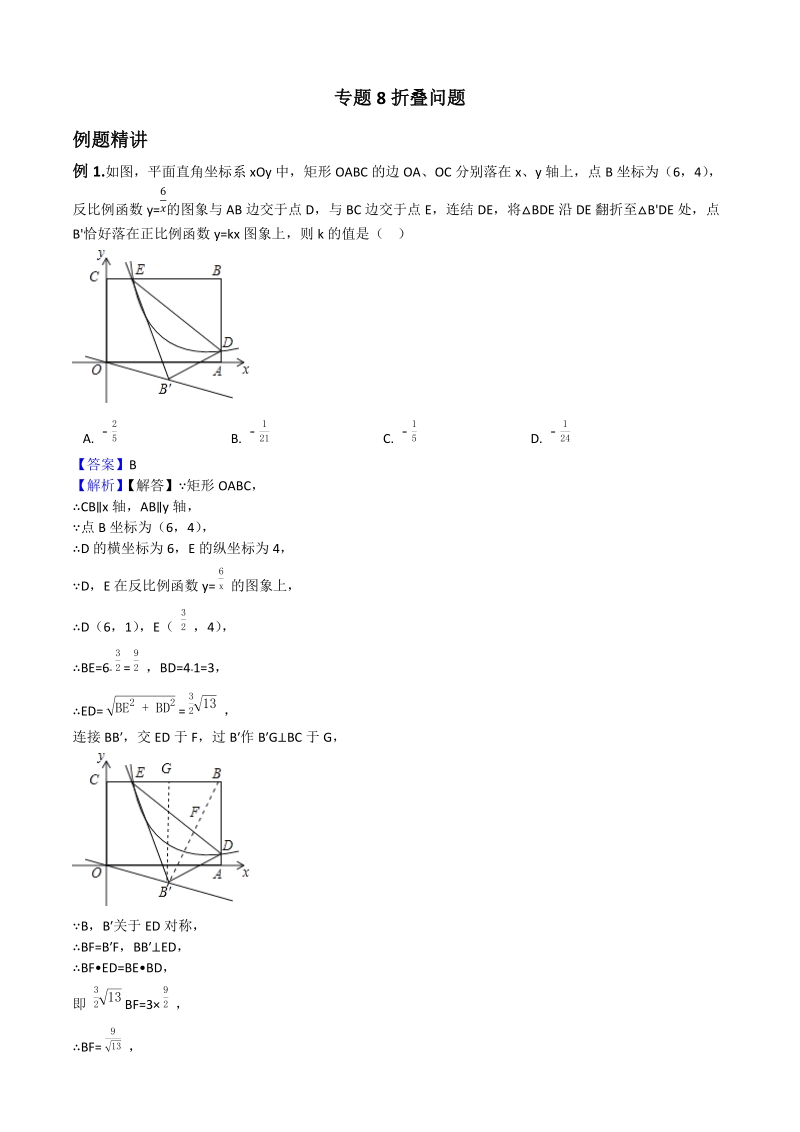
1、专题 8 折叠问题例题精讲例 1.如图，平面直角坐标系 xOy 中，矩形 OABC 的边 OA、OC 分别落在 x、y 轴上，点 B 坐标为（6 ，4） ，反比例函数 y= 的图象与 AB 边交于点 D，与 BC 边交于点 E，连结 DE，将 BDE 沿 DE 翻折至BDE 处，点6B恰好落在正比例函数 y=kx 图象上，则 k 的值是（ ）A. B. C. D. -25 -121 -15 -124【答案】B 【解析】 【解答】矩形 OABC，CBx 轴，ABy 轴，点 B 坐标为（ 6，4） ，D 的横坐标为 6，E 的纵坐标为 4，D，E 在反比例函数 y= 的图象上，6xD（6， 1）
2、，E（ ，4） ，32BE=6 = ， BD=41=3，32 92ED= = ，BE2+BD23213连接 BB，交 ED 于 F，过 B作 BGBC 于 G， B，B 关于 ED 对称，BF=BF，BBED ，BFED=BEBD，即 BF=3 ，3213 92BF= ，913BB= ，1813设 EG=x，则 BG= x，92BB2BG2=BG2=EB2GE2 ， （ ） 2（ x） 2=（ ） 2x2 ， 1813 92 92x= ，4526EG= ，4526CG= ，4213BG= ，5413B（ ， ） ，4213 213k= 121故答案为：B例 2.如图，在梯形 ABCD 中，AD
3、 BC，AD=2 ，AB=3，BC=6，沿 AE 翻折梯形 ABCD 使点 B 落 AD 的延长线上，记为点 B，连接 BE交 CD 于点 F，则 的值为（ )DFFCA. B. C. D. 13 14 15 16【答案】 A 【解析】【 分析 】 利用折叠，将线段和角进行转化，即 AB=AB，BAE= BAE，利用线段的和差关系求 DB；根据ADBC，得BAE=BEA，从而可证 AB=BE，再计算 EC，根据平行得相似比，求 的值DFFC【解答】由折叠的性质可知，AB=AB，BAE=BAE，DB=AB-AD=3-2=1，又 ADBC，BAE=BEA，BAE=BEA， BE=AB=3EC=BC
4、=BE=6-3=3，DBEC， = = DFFCDBEC13故选 A例 3.如图，在折纸活动中，小明制作了一张 ABC 纸片，点 D、E 分别是边 AB、AC 上，将ABC 沿着 DE折叠压平，A 与 A重合，若A=75，则1+ 2=（ ） A. 150 B. 210 C. 105 D. 75【答案】A 【解析】 【解答】解：ADE 是ABC 翻折变换而成， AED=AED，ADE=ADE，A= A=75，AED+ADE=AED+ADE=18075=105，1+2=3602105=150故选 A例 4.如图，在等边ABC 中， BC=6，点 D，E 分别在 AB，AC 上，DEBC，将 ADE
5、 沿 DE 翻折后，点 A 落在点 A处连结 A A并延长，交 DE 于点 M，交 BC 于点 N如果点 A为 MN 的中点，那么 ADE 的面积为（ ）A. B. 3 C. 6 D. 9 3 3 3 3【答案】 A 【解析】 【解答】解：ADE 沿 DE 翻折后，点 A 落在点 A处AM=AM，又 A为 MN 的中点，AM=AM=AN，DEAC， = ，AMANAEACABC 是等边三角形，BC=6，BC=AC， = 13 AE6AE=2，AN 是ABC 的 BC 边上的高，中线及角平分线，MAE=30，AM= ，ME=1，3DE=2，ADE 的面积= DEAM= 2= ，12 12 3 3
6、故答案为：A例 5.如图，在矩形 AOBC 中，O 为坐标原点，OA、OB 分别在 x 轴、y 轴上，点 B 的坐标为（0，3 ） ，3ABO=30，将ABC 沿 AB 所在直线对折后，点 C 落在点 D 处，则点 D 的坐标为_【答案】( , ) 32323【解析】 【解答】解：四边形 AOBC 是矩形， ABO=30，点 B 的坐标为（0 ，3 ） ，3AC=OB=3 ， CAB=30，3BC=ACtan30=3 =3，333将 ABC 沿 AB 所在直线对折后，点 C 落在点 D 处，BAD=30，AD=3 ，3过点 D 作 DMx 轴于点 M，CAB=BAD=30，DAM=30，DM=
7、 AD= ，12 332AM=ADcos30= ，92MO= -3= ，92 32点 D 的坐标为（ ， ） 32 332故答案为：（ ， ） 32 332习题精炼1.如图，矩形 EFGH 四个顶点分别在菱形 ABCD 的四条边上， BE=BF，将AEH ，CFG 分别沿边 EH，FG 折叠，当重叠部分为菱形且面积是菱形 ABCD 面积的 时，则 为（ ）116 AEEBA. B. 2 C. D. 453 522.如图，矩形纸片 ABCD 中，AB=4，BC=6 ，将 ABC 沿 AC 折叠，使点 B 落在点 E 处，CE 交 AD 于点 F，则DF 的长等于（ ）A. B. C. D. 35
8、 53 73 543.如图，点 E 在正方形 ABCD 的 CD 边上，连结 BE，将正方形折叠，使点 B 与 E 重合， 折痕 MN 交 BC 边于点 M，交 AD 边于点 N，若 tanEMC ，MECE8 ，则折痕 MN 的长为（ ）34A. B. 4 C. 3 D. 1353 5 104.如图，Rt ABC 中，AB=9 ，BC=6 ， B=90，将ABC 折叠，使 A 点与 BC 的中点 D 重合，折痕为 PQ，则线段 BQ 的长度为（ ） A. B. C. 4 D. 553 525.如图，在矩形 ABCD 中，ADAB，将矩形 ABCD 折叠，使点 C 与点 A 重合，折痕为 MN
9、，连接 CN若CDN 的面积与CMN 的面积比为 1：4，则 的值为（ ） MNBMA. 2 B. 4 C. D. 25 266.如图所示，在矩形纸片 中， ， 为 边上两点，且 ； ， 为 边上ABCD E G AB AE=EG=GB F H CD两点，且 沿虚线 折叠，使点 落在点 上，点 落在点 上；然后再沿虚线 DF=FH=HC EF A G D H折叠，使 落在点 上，点 落在点 上叠完后，剪一个直径在 上的半圆，再展开，则展GH B E C F EF开后的图形为（ ）A. B. C. D. 7.如图，长方形纸片 ABCD，AB=a，BC=b，且 ba2b，则 ADC 的平分线 DE
10、 折叠纸片，点 A 落在 CD 边上的点 F 处，再沿 BEF 的平分线 EG 折叠纸片，点 B 落在 EF 边上的点 H 处，则四边形 CGHF 的周长是（ ）A. 2a B. 2b C. 2（ab） D. a+b8.如图，把一张矩形纸片 ABCD 沿对角线 AC 折叠，点 B 的对应点为 B，AB与 DC 相交于点 E，则下列结论一定正确的是（ ） A. DAB=CAB B. ACD=BCD C. AD=AE D. AE=CE9.如图，将矩形纸片 ABCD 沿其对角线 AC 折叠，使点 B 落到点 B的位置，AB与 CD 交于点 E，若AB=8， AD=3，则图中阴影部分的周长为（ ） A
11、. 16 B. 19 C. 22 D. 2510.取一张矩形的纸片进行折叠，具体操作过程如下： 第一步：先把矩形 ABCD 对折，折痕为 MN，如图（1 ） ；第二步：再把 B 点叠在折痕线 MN 上，折痕为 AE，点 B 在 MN 上的对应点为 B，得 RtABE，如图（2 ） ；第三步：沿 EB线折叠得折痕 EF，如图（3） 若 AB= ，则 EF 的值是（ ）3A. 1 B. 2 C. 3 D. 411.如图，对折矩形纸片 ABCD，使 AB 与 DC 重合得到折痕 EF，将纸片展平；再一次折叠，使点 D 落到 EF上点 G 处，并使折痕经过点 A，展平纸片后DAG 的大小为（ ）A.
12、30 B. 45 C. 60 D. 7512.如图，矩形 ABCD 与菱形 EFGH 的对角线均交于点 O，且 EGBC，将矩形折叠，使点 C 与点 O 重合，折痕 MN 恰好过点 G 若 AB= ，EF=2，H=120，则 DN 的长为（ ） 6A. B. C. D. 2 32 6+32 6 3 3 613.如图，把一张矩形纸片 ABCD 沿 EF 折叠后，点 A 落在 CD 边上的点 A处，点 B 落在点 B处，若2=40，则图中1 的度数为（ ）A. 115 B. 120 C. 130 D. 14014.如图，把矩形纸片 ABCD 沿 EF 翻折，点 A 恰好落在 BC 边的 A处，若
13、AB= ，EFA=60，则四边形3ABEF的周长是（ ） A. 1+3 B. 3+ C. 4+ D. 5+ 3 3 3 315.如图，将正方形 ABCD 折叠，使顶点 A 与 CD 边上的一点 H 重合（H 不与端点 C，D 重合） ，折痕交 AD于点 E，交 BC 于点 F，边 AB 折叠后与边 BC 交于点 G，如果正方形 ABCD 的边长为 1，则 CHG 的周长为_16.如图，有一块平行四边形纸片 ABCD，现将其折叠，使得 AB 落在 AD 上点 F 处，折痕为 AE，再将AEF沿 EF 翻折，若点 A 刚好落在 CD 边上点 G 处，则 =_。ABBC17.如图，在矩形 ABCD
14、中，AB=4，点 E，F 分别在 BC，CD 上，将ABE 沿 AE 折叠，使点 B 落在 AC 上的点B处，又将CEF 沿 EF 折叠，使点 C 落在直线 EB与 AD 的交点 C处，DF=_ 18.如图，矩形纸片 ABCD 中，AB=5，BC=3 ，先按图（2）操作：将矩形纸片 ABCD 沿过点 A 的直线折叠，使点 D 落在边 AB 上的点 E 处，折痕为 AF；再按图（3 ）操作，沿过点 F 的直线折叠，使点 C 落在 EF 上的点 H 处，折痕为 FG，则 A、H 两点间的距离为_ 19.如图，点 E、 F 分别是正方形纸片 ABCD 的边 BC、CD 上一点，将正方形纸片 ABCD
15、 分别沿 AE、AF 折叠，使得点 B、D 恰好都落在点 G 处，且 EG=2，DC=6，则 FG= _. 20.如图，四边形 ABCD 是矩形纸片，AB=2，对折矩形纸片 ABCD，使 AB 与 CD 重合，折痕为 MN，展平后再过点 B 折叠矩形纸片，使点 A 落在 MN 上的点 G 处，折痕 BE 与 MN 相交于点 H；再次展平，连接BG，EG，延长 EG 交 BC 于点 F有如下结论：EG=FG；ABG=60 ；AE=1； BEF 是等边三角形；其中正确结论的序号是_21.如图，AC 是矩形 ABCD 的对角线， O 是 ABC 的内切圆，现将矩形 ABCD 按如图所示的方式折叠，使
16、点 D 与点 O 重合，折痕为 FG，点 F，G 分别在 AD，BC 上，连结 OG，DG，若 OGDG，且O 的半径长为1，则 BC+AB 的值 _ 22.如图，在矩形 ABCD 中，AB=4，BC=6 ，点 E 为 BC 的中点，将ABE 沿 AE 折叠，使点 B 落在矩形内点 F处，连接 CF，则 CF 的长为_ 23.如图，矩形 ABCD 中，AB=8，BC=15，点 E 是 AD 边上一点，连接 BE，把ABE 沿 BE 折叠，使点 A 落在点 A处，点 F 是 CD 边上一点，连接 EF，把 DEF 沿 EF 折叠，使点 D 落在直线 EA上的点 D处，当点 D落在 BC 边上时，
17、AE 的长为_ 答案解析部分一、单选题1.【答案】 A 【解析】 【解答】解：依题可得阴影部分是菱形.设 S 菱形 ABCD=16,BE=x.AB=4.阴影部分边长为 4-2x.（ 4-2x） 2=1.4-2x=1 或 4-2x=-1.x= 或 x= （舍去） .32 52 = = .AEEB4-3232 53故答案为 A.【分析】依题可得阴影部分是菱形.设 S 菱形 ABCD=16,BE=x.从而得出 AB=4，阴影部分边长为 4-2x.根据（4-2x） 2=1 求出 x,从而得出答案 .2.【答案】 B 【解析】 【解答】解：由题意得：EC=BC=6，AE=AB=4，BCA=FCA，四边形
18、 ABCD 是矩形，ADBC,AB=CD,FAC=BCA,FAC=FCA,AF=CF，AD-AF=CE-CF，即 DF=FE设 DF=FE=x，CF=6-x，在 RtCDF 中， DF2+CD2=CF2即 ， x2+42=(6-x)2解得：x= ,53即 DF= .53故选 B.【分析】根据折叠前后的图形是全等形，得出 EC=BC=6， AE=AB=4，BCA=FCA，再根据 ADBC，从而得出FAC=BCA ，FAC= FCA, AF=CF，DF=FE在 RtCDF 中，根据勾股定理得出 DF 的长度即可。3.【答案】 C 【解析】 【解答】解：四边形 ABCD 是正方形， C= D= A=
19、90， BC=CD=AD，在 RtMCE 中 , tan EMC=ECMC=34，即 ECMC=34,设 根据勾股定理可知： EC=3x,MC=4x, ME=BM=5x,ME+CE=8，解得： 3x+5x=8, x=1.CE=3， MC=4,ME=BM=5,即 BC=AD=CD=9，DE=6，由折叠的性质可得： A1N=AN, A1= A=90,A1E=AB， FEM= ABM=90， DFE+ DEF= DEF+ CME=90， A1NF= DFE= CME， DF=DEtan DFE=634=92，EF= DE2+DF2=152, A1F=A1E-EF=9-152=32， A1N=A1Ft
20、an A1NF=2， AN=A1N=2.过点 作 , N NH BCBH=AN=2,HM=AB-BH=3,MN= NH2+HM2= 92+32= 90=310.故答案为：C.【分析】过点 N 作 NHBC ,在 RtMCE 中, 由 tanEMC= 可求得 ，设 EC=3x，MC=4x，根据勾股定理ECMC ECMC=34和折叠的性质可得：ME=BM=5x，由题意 MECE8 可求得 x 的值，于是解直角三角形 DEF 可求得 DF 和EF 的值，根据线段的构成可得 F= EEF，解直角三角形 NF 可求出 N 的值，则由折叠的性质可得 AN=A1 A1 A1 A1N，解直角三角形 MNH 即
21、可求得 MN 的值。A14.【答案】 C 【解析】 【解答】解：设 BQ=x，由折叠的性质可得 DQ=AQ=9x， D 是 BC 的中点，BD=3，在 RtBQD 中，x 2+32=（9 x） 2 ， 解得：x=4故线段 BQ 的长为 4故选：C【分析】设 BQ=x，则由折叠的性质可得 DQ=AQ=9x，根据中点的定义可得 BD=3，在 RtBQD 中，根据勾股定理可得关于 x 的方程，解方程即可求解此题考查了翻折变换（折叠问题） ，折叠的性质，勾股定理，中点的定义以及方程思想，综合性较强5.【答案】 D 【解析】 【解答】解：过点 N 作 NGBC 于 G， 四边形 ABCD 是矩形，四边形
22、 CDNG 是矩形，AD BC，CD=NG，CG=DN， ANM=CMN，由折叠的性质可得：AM=CM，AMN= CMN，ANM=AMN，AM=AN，四边形 AMCN 是平行四边形，AM=CM，四边形 AMCN 是菱形，CDN 的面积与CMN 的面积比为 1：4 ，DN：CM=1 ：4，设 DN=x，则 AN=AM=CM=CN=4x，AD=BC=5x，CG=x，BM=x，GM=3x，在 RtCGN 中，NG= ，CN2+CG2= 15x在 RtMNG 中，MN= ，GM2+NG2=26x = MNBM26故选 D【分析】首先过点 N 作 NGBC 于 G，由四边形 ABCD 是矩形，易得四边形
23、 CDNG 是矩形，又由折叠的性质，可得四边形 AMCN 是菱形，由 CDN 的面积与 CMN 的面积比为 1：4 ，根据等高三角形的面积比等于对应底的比，可得 DN：CM=1：4，然后设 DN=x，由勾股定理可求得 MN 的长，继而求得答案6.【答案】 B 【解析】 【解答】解：由折叠的性质知，展开后是 B，故选 B7.【答案】 B 【解析】 【解答】解：由折叠得：DF=AD=b，BE=EH，FC=DC DF=ABDF=ab，四边形 ABCD 是矩形，ADC=A=90，DE 平分 ADC，ADE=EDC=45，DCAB，EDC= AED=45，由折叠得：AED= DEF=45，AEF=90，
24、ADC=A= AEF=90，四边形 DAEF 是矩形，同理四边形 CFEB 是矩形，四边形 CFHG 是矩形，BE=FC=ab，AD=EF=b ， EH=BE=ab，FH=EFEH=b（a b）=2ba，四边形 CGHF 的周长是：2FC+2FH=2（a b）+2 （2ba）=2b；故选 B8.【答案】 D 【解析】 【解答】解：矩形纸片 ABCD 沿对角线 AC 折叠，点 B 的对应点为 B， BAC=CAB，ABCD，BAC=ACD，ACD=CAB，AE=CE，所以，结论正确的是 D 选项故选 D【分析】根据翻折变换的性质可得BAC=CAB，根据两直线平行，内错角相等可得 BAC=ACD，
25、从而得到ACD=CAB，然后根据等角对等边可得 AE=CE，从而得解9.【答案】C 【解析】 【解答】解：四边形 ABCD 为矩形， BC=BC=AD，B= B=D=90BEC=DEA，在AED 和 CEB中， BEC= DEA B= DBC=ADAEDCEB（AAS） ；EA=EC，阴影部分的周长为 AD+DE+EA+EB+BC+EC，=AD+DE+EC+EA+EB+BC，=AD+DC+AB+BC，=3+8+8+3，=22，故选 C【分析】首先由四边形 ABCD 为矩形及折叠的特性，得到 BC=BC=AD， B=B=D=90， BEC=DEA，得到AED CEB，得出 EA=EC，再由阴影部
26、分的周长为 AD+DE+EA+EB+BC+EC，即矩形的周长解答即可10.【 答案】 B 【解析】 【解答】解：如图所示，将图 3 展开，可得图 4， 由折叠可得，RtAMB中，AM= AB= AB，12 12ABM=30，BAE=BAE=30，EAF=60，AEB=60= AEB，AEF 是等边三角形，EF=AE=2BE，又 RtABE 中，AB= ，3BE=1，EF=2，故选：B【分析】根据折叠得到AEF 是等边三角形，再根据 RtABE 中，AB= ，即可得到 EF 的长311.【 答案】 C 【解析】 【解答】解：如图所示：由题意可得：1= 2，AN=MN，MGA=90，则 NG= A
27、M，故 AN=NG，12则2= 4，EFAB，4=3，1=2=3= 90=30，13DAG=60故选：C【分析】直接利用翻折变换的性质以及直角三角形的性质得出2= 4，再利用平行线的性质得出1=2=3，进而得出答案此题主要考查了翻折变换的性质以及平行线的性质，正确得出 2=4 是解题关键12.【 答案】 C 【解析】 【解答】解：长 EG 交 DC 于 P 点，连接 GC、FH；如图所示：则 CP=DP= CD= ， GCP 为直角三角形，四边形 EFGH 是菱形， EHG=120，GH=EF=2，OHG=60，EGFH，OG=GHsin60=2 = ，由折叠的性质得：CG=OG= ，OM=C
28、M，MOG=MCG ，PG= = ，OGCM，MOG+OMC=180，MCG+OMC=180，OMCG，四边形 OGCM 为平行四边形，OM=CM，四边形 OGCM 为菱形，CM=OG= ，根据题意得：PG 是梯形 MCDN 的中位线，DN+CM=2PG= ，DN= ；故选：C【分析】延长 EG 交 DC 于 P 点，连接 GC、FH，则GCP 为直角三角形，证明四边形 OGCM 为菱形，则可证 OC=OM=CM=OG= ，由勾股定理求得 GP 的值，再由梯形的中位线定理 CM+DN=2GP，即可得出答案本题考查了矩形的性质、菱形的性质、翻折变换的性质、勾股定理、梯形中位线定理、三角函数等知识
29、；熟练掌握菱形和矩形的性质，由梯形中位线定理得出结果是解决问题的关键13.【 答案】 A 【解析】 【解答】解：把一张矩形纸片 ABCD 沿 EF 折叠后，点 A 落在 CD 边上的点 A处，点 B 落在点 B处，BFE=EFB，B= B=90，2=40，CFB=50，1+EFBCFB=180，即1+ 150=180，解得：1=115，故选 A【分析】根据折叠的性质和矩形的性质得出BFE= EFB，B= B=90，根据三角形内角和定理求出CFB=50，进而解答即可本题考查了矩形的性质，折叠的性质，三角形的内角和定理的应用，能综合运用性质进行推理和计算是解此题的关键，注意：折叠后的两个图形全等1
30、4.【 答案】D 【解析】 【解答】解：如图， 过点 E 作 EGAD，AGE=FGE=90矩形纸片 ABCD，A=B=AGE=90，四边形 ABEG 是矩形，BE=AG，EG=AB= ，3在 RtEFG 中，EFG=60 ，EG= ，3FG=1， EF=2，由折叠有，AF=AF，AB=AB= ，BE=BE，AFE=AFE=60，3BCAD，AEF=AFE=60，AEF 是等边三角形，AF=EF=2，AF=AF=2，BE=AG=AFFG=21=1BE=1四边形 ABEF的周长是 AB+BE+EF+AF= +1+2+2=5+ ，3 3故选 D【分析】先在直角三角形 EFG 中用勾股定理求出 EF
31、，FG，再判断出三角形 AEF 是等边三角形，求出 AF，从而得出 BE=BE=1，最后用四边形的周长公式即可二、填空题15.【 答案】 2 【解析】 【解答】解：设 CH=x，DE=y，则 DH=1-x，EH=1-y，EHG=90，DHE+CHG=90DHE+DEH=90，DEH=CHG，又D=C=90，DEHCHG，CG：DH=CH：DE=HG：EH，即 CG:(1x)=x:y=HG:(1y)，CG= ， HG= ，x(1-x)y x(1-y)yCMG 的周长为=CH+CG+HG= ，2x-x2y在 RtDEH 中，DH 2+DE2=EH2,即（1-x） 2+y2=（1-y） 2,整理得
32、2x-x2=2y，CH+HG+CG= 2x-x2y =2yy=2故答案为：2【分析】设 CH=x，DE=y，由题意易证得DEH CHG，由所得的比例式可将 HG、CG 用含 x、y 的代数式表示，在 RtDEH 中，用勾股定理可得 x 与 y 的关系 式，则CHG 的周长=CH+HG+CG 可求解。16.【 答案】12【解析】 【解答】解：由第一折叠可得 AB=AF，BE=EF，BAE= FAE，在ABCD 中，AD/BC，DAE= AEB，BAE=AEB，AB=BE，AB=BE=EF=AF，四边形 ABEF 是菱形，EF/AB/CD。连接 AC 交 EF 于 O，由第二次折叠可得 AO=OG
33、，OF 是AGD 的中位线，AF= AD，AB= BC，12 12即 。ABBC=12故答案为 。12【分析】把 3 副图合在一起，更能看出一些边、角的关系，根据第一次折叠和平行线的性质可得四边形ABEF 是菱形，则 EF/CD，根据第 2 次折叠，可得 EF 平分 AG，则可得 OF 是AGD 的中位线，即 AF= AD，12而 AF=AB，AD=BC。17.【 答案】 43【解析】 【解答】解：连接 CC， 将 ABE 沿 AE 折叠，使点 B 落在 AC 上的点 B处，又将CEF 沿 EF 折叠，使点 C 落在 EB与 AD 的交点 C处EC=EC，1=2，3=2，1=3，在CCB与CC
34、D 中， ， D= CBC=90 BCC= DCCCC=CCCCBCCD，CB=CD，又 AB=AB，AB=CB，所以 B是对角线 AC 中点，即 AC=2AB=8，所以ACB=30，BAC=60， ACC=DCC=30，DCC=1=60，DCF=FCC=30，CF=CF=2DF，DF+CF=CD=AB=4，DF= 43故答案为： 43【分析】首先连接 CC，可以得到 CC是ECD 的平分线，所以 CB=CD，又 AB=AB，所以 B是对角线中点，AC=2AB，所以 ACB=30，即可得出答案18.【 答案】 10【解析】 【解答】解：如图 3 中，连接 AH 由题意可知在 RtAEH 中，A
35、E=AD=3，EH=EFHF=3 2=1，AH= = = ，AE2+EH2 32+12 10故答案为 10【分析】如图 3 中，连接 AH由题意可知在 RtAEH 中，AE=AD=3，EH=EFHF=32=1 ，根据 AH= ，计算即可AE2+EH219.【 答案】 3 【解析】 【解答】四边形 ABCD 是正方形，DC=6， C=90，BC=DC=6 ，设 FG= ，x由折叠的性质可得：DF= ，BE=EG=2，xEF=EG+GF= ，EC=BC-BE=6-2=4，CF=DC-DF= ，x+2 6-x在 RtEFC 中， EF2=EC2+FC2 ， ，解得： ，(x+2)2=42+(6-x)
36、2 x=3FG=3.故答案为：3.【分析】根据正方形的性质，可知B=90及 BC 的长，设 FG=x，由折叠的性质可得：DF= ，BE=EG=2 ，再x用含 x 的代数式表示出 EF、FC，求出 EC 的长，利用勾股定理建立关于 x 的方程，解方程即可。20.【 答案】 【解析】 【解答】解：如图，连接 AG MN 垂直平分 AB，ADBCMN，AG=BG，EG=FG ，正确，根据折叠的性质，可得AB=BG，AG=AB=BGABG 为等边三角形ABG=60，EDG=602=30，即结论正确；ABG=60， ABE=GBE，ABE=GBE=602=30，AE=ABtan30=2 = ，33 23
37、3即结论不正确；ABE=EBG=30，BGE= BAE=90，BEG=BGEEBG=9030=60，EBF=ABFABE=9030=60，BFE=1806060=60，EBF=BEG=BFE=60，BEF 为等边三角形，即结论正确；故答案为：【分析】由折叠的性质和梯形的性质得出 相切；周长ABG 为等边三角形，得出 正确；由三角函数求出 AE，得出 不正确；证出EBF= BEG=BFE=60，得出正确；即可得出答案21.【 答案】 2 +4 3【解析】 【解答】解：如图所示：设圆 0 与 BC 的切点为 M，连接 OMBC 是圆 O 的切线，M 为切点，OMBCOMG=GCD=90由翻折的性质
38、可知：OG=DGOGGD，OGM+DGC=90又MOG+OGM=90，MOG=DGC在OMG 和GCD 中， ， OMG= DCG=90 MOG= DGCOG=DG OMGGCDOM=GC=1CD=GM=BCBMGC=BC2AB=CD，BCAB=2设 AB=a，则 BC=a+2圆 O 是ABC 的内切圆，AC=AB+BC2rAC=2a = ABBC12ACB=30 = ， 即 = ABBC33 aa+2 33解得：a= 3+1AB= ， BC=AB+2= 3+1 3+3所有 AB+BC=4+ 23故答案为：4+ 23【分析】设圆 0 与 BC 的切点为 M，连接 OM，由切线的性质可知 OMBC，然后证明OMGGCD，得到OM=GC=1，CD=GM=BCBMGC=BC2 设 AB=a，BC=a+2，AC=2a，从而可求得ACB=30 ，从而得到 = ， ABBC33故此可求得 AB= ， 则 BC= 3+1 3+322.【 答案】 185【解析】 【解答】解：连接 BF， BC=6，点
