1、2019 年湖北省黄冈中学启黄初中中考数学模拟试卷一、填空题（每小题 3 分，共 24 分）1tan60 2已知：x 24x +4 与| y1| 互为相反数，则式子 的值等于 3函数 中的自变量 x 的取值范围是 4据统计，2018 年黄冈市人均 GDP 约为 1.15104 元，近似数 1.15104 有 个有效数字5分解因式：xy 22x 2y+x3 6将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上，则1+2 7如图，在平面直角坐标系中，点 O 为原点，菱形 OABC 的对角线 OB 在 x 轴上，顶点A 在反比例函数 y 的图象上，则菱形的面积为
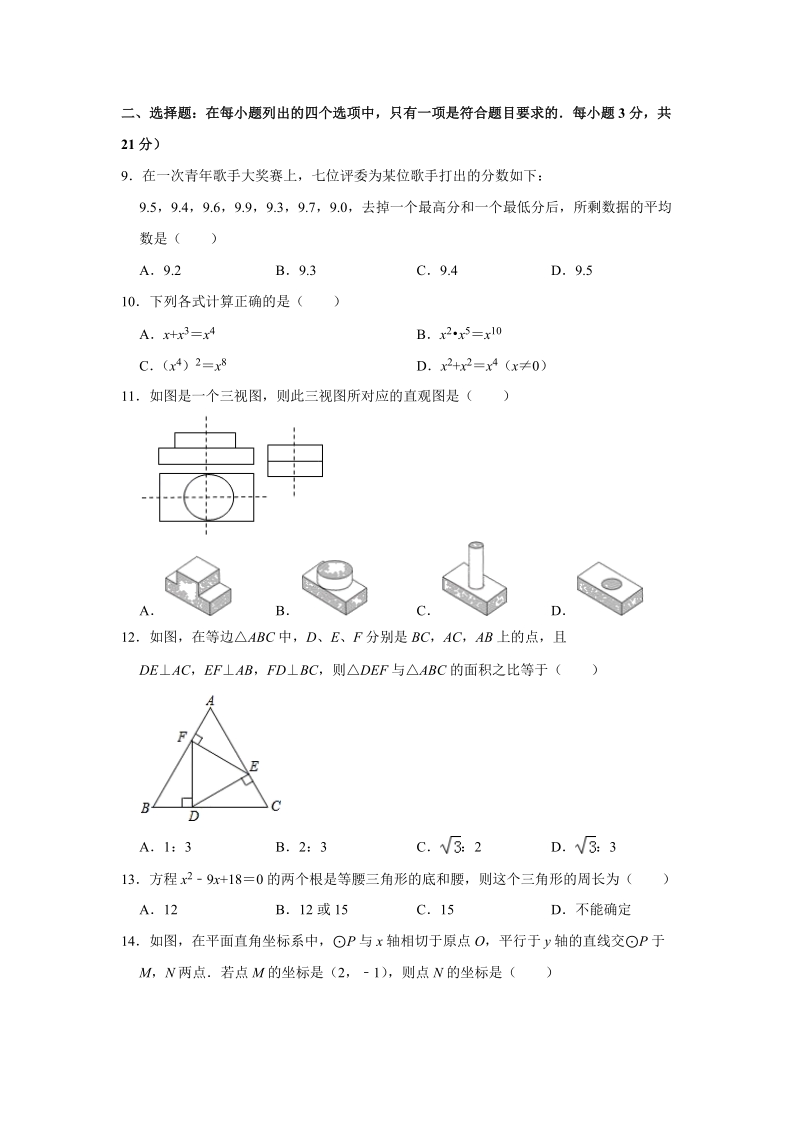
2、 8如图，ABCD 中，ACCD，以 C 为圆心，CA 为半径作圆弧交 BC 于 E，交 CD 的延长线于点 F，以 AC 上一点 O 为圆心 OA 为半径的圆与 BC 相切于点 M，交 AD 于点N若 AC9cm，OA3cm ，则图中阴影部分的面积为 cm 2二、选择题：在每小题列出的四个选项中，只有一项是符合题目要求的每小题 3 分，共21 分）9在一次青年歌手大奖赛上，七位评委为某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0，去掉一个最高分和一个最低分后，所剩数据的平均数是（ ）A9.2 B9.3 C9.4 D9.510下列各式计算正确的是（ ）Ax+x
3、3x 4 Bx 2x5x 10C （x 4） 2x 8 Dx 2+x2x 4（x0）11如图是一个三视图，则此三视图所对应的直观图是（ ）A B C D12如图，在等边ABC 中，D、E、F 分别是 BC，AC ，AB 上的点，且DEAC ，EF AB，FD BC，则DEF 与ABC 的面积之比等于（ ）A1：3 B2：3 C ：2 D ：313方程 x29x +180 的两个根是等腰三角形的底和腰，则这个三角形的周长为（ ）A12 B12 或 15 C15 D不能确定14如图，在平面直角坐标系中，P 与 x 轴相切于原点 O，平行于 y 轴的直线交P 于M，N 两点若点 M 的坐标是（ 2，
4、1） ，则点 N 的坐标是（ ）A （2，4） B （2，4.5） C （2，5） D （2，5.5）15如图，BC 是A 的内接正十边形的一边，BD 平分 ABC 交 AC 于点 D，则下列结论正确的有（ ）BC BDAD；BC 2DCAC ；AB2AD ；BC ACA1 个 B2 个 C3 个 D4 个三、解答题：（本大题共 8 小题，满分 55 分.解答应写出文字说明、证明过程或演算步骤.）16解不等式组： 17 （某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，下图是根据这组数据绘制的统计图，图中从左到右各长方形高度之比为 3：4：5：8：2
5、，又知此次调查中捐 15 元和 20 元的人数共 39 人（1）他们一共抽查了多少人捐款数不少于 20 元的概率是多少？（2）这组数据的众数、中位数各是多少？（3）若该校共有 2310 名学生，请估算全校学生共捐款多少元？18已知：如图，在梯形 ABCD 中，ADBC，BCDC，CF 平分BCD，DFAB，BF的延长线交 DC 于点 E求证：（1）BFCDFC；（2）ADDE19一个不透明的布袋里装有 4 个大小、质地均相同的乒乓球，每个球上面分别标有1，2，3，4小林先从布袋中随机抽取一个乒乓球（不放回去） ，再从剩下的 3 个球中随机抽取第二个乒乓球，记两次取得乒乓球上的数字依次为 a、b
6、（1）求 a、b 之积为偶数的概率；（2）若 c5，求长为 a、b、c 的三条线段能围成三角形的概率20某公司投资新建了一商场，共有商铺 30 间据预测，当每间的年租金定为 10 万元时，可全部租出每间的年租金每增加 5000 元，少租出商铺 1 间该公司要为租出的商铺每间每年交各种费用 1 万元，未租出的商铺每间每年交各种费用 5000 元（1）当每间商铺的年租金定为 13 万元时，能租出多少间？（2）当每间商铺的年租金定为多少万元时，该公司的年收益（收益租金各种费用）为 275 万元？21已知，如图，直线 MN 交O 于 A，B 两点，AC 是直径， AD 平分CAM 交O 于D，过 D
7、作 DEMN 于 E（1）求证：DE 是O 的切线；（2）若 DE6cm ，AE3cm，求 O 的半径22如图，泰州园博园中有一条人工河，河的两岸 PQ、MN 互相平行，河岸 PQ 上有一排间隔为 50 米的彩灯柱 C、D、E、，某人在河岸 MN 的 A 处测得DAN21，然后沿河岸走了 175 米到达 B 处，测得CBN45，求这条河的宽度 （参考数据：， ）23某公司开发了一种新型的家电产品，又适逢“家电下乡”的优惠政策现投资 40 万元用于该产品的广告促销，已知该产品的本地销售量 y1（万台）与本地的广告费用 x（万元）之间的函数关系满足 y1 该产品的外地销售量 y2（万台）与外地广告
8、费用 t（万元）之间的函数关系可用如图所示的抛物线和线段 AB 来表示其中点 A 为抛物线的顶点（1）结合图象，求出 y2（万台）与外地广告费用 t（万元）之间的函数关系式；（2）求该产品的销售总量 y（万台）与本地广告费用 x（万元）之间的函数关系式；（3）如何安排广告费用才能使销售总量最大？24如图，已知对称轴为直线 x4 的抛物线交 x 轴于点 A、B（点 A 在 B 左侧） ，且点 B坐标为（6，0） ，过点 B 的直线交抛物线于点 C（3，4） （1）写出点 A 坐标；（2）求抛物线解析式；（3）若点 P 在抛物线的 BC 段上，则 x 轴上时否存在点 Q，使得以 Q、B、P 、C
9、为顶点的四边形是平行四边形？若存在，请分别求出点 P、Q 坐标；若不存在，请说明理由；（4）若点 M 在线段 AB 上以每秒 1 个单位长度的速度从 A 向 B 运动，同时，点 N 在射线 BC 上以每秒 2 个单位长度的速度从 B 向 C 运动，当其中一个点停止运动时，另一个点也随之停止运动设运动时间为 t 秒，当 t 为何值，以 M、N 、B 为顶点的三角形与ABC 相似，写出计算过程参考答案一、填空题（每小题 3 分，共 24 分）1 【解答】解：tan60 ，tan60 故答案为： 2 【解答】解：x 24x +4 与| y1|互为相反数，x 24x+4+|y1|0（x2） 2+|y1
10、|0（x2） 20，|y1| 0x2，y1（ ）（x+y ）（2 ）（2+1） 故答案为： 3 【解答】解：根据题意得：x30，解得：x3；故答案为 x34 【解答】解：近似数 1.15104 的有效数字就是 1.15 的有效数字，即 1，1，5 共 3 个故答案为 35 【解答】解：xy 22x 2y+x3x （y 22xy+x 2）x（yx） 2故答案为：x（y x ） 26 【解答】解：如图，连接两交点，根据矩形两边平行，得1+2+3+4180，又矩形的角等于 90，3+490，1+21809090故答案为：907 【解答】解：连接 AC 交 OB 于 D四边形 OABC 是菱形，ACO
11、B点 A 在反比例函数 y 的图象上，AOD 的面积 21 ，菱形 OABC 的面积4AOD 的面积48 【解答】解：连接 OM，ON OM 3，OC6，ACM30，CDAB 3 ，扇形 ECF 的面积 27；ACD 的面积ACCD2 ；扇形 AOM 的面积 3；弓形 AN 的面积 3 3 ；OCM 的面积 33 ；阴影部分的面积扇形 ECF 的面积ACD 的面积OCM 的面积扇形 AOM 的面积弓形 AN 的面积（ 21 ）cm 2故答案为 21 二、选择题：在每小题列出的四个选项中，只有一项是符合题目要求的每小题 3 分，共21 分）9 【解答】解：平均数是 9.5 分故选：D10 【解答
12、】解：A、x 与 x3 不是同类项不能合并，故本选项错误；B、应为 x2x5x 2+5x 7，故本选项错误；C、 （x 4） 2x 42x 8，故本选项正确；D、应为 x2+x22x 2，故本选项错误；故选：C11 【解答】解：从俯视图可以看出直观图的下面部分为长方体，上面部分为圆柱，且与下面的长方体的高度相同只有 B 满足这两点，故选 B12 【解答】解：DEAC，EFAB，FDBC ，C+EDC90，FDE+EDC90，CFDE ，同理可得：BDFE ，ADEF ，DEFCAB，DEF 与ABC 的面积之比（ ） 2，又ABC 为正三角形，BCA60，EFD 是等边三角形，EFDE DF，
13、又DEAC，EF AB，FDBC ，AEF CDEBFD，BFAECD，AFBDEC ，在 Rt DEC 中，DEDCsinC DC，EC cos C DC DC，又DC+BD BCAC DC， ，DEF 与ABC 的面积之比等于：（ ） 2 1：3故选：A13 【解答】解：解方程 x29x+180，得 x16，x 23当底为 6，腰为 3 时，由于 3+36，不符合三角形三边关系等腰三角形的腰为 6，底为 3周长为 6+6+315故选：C14 【解答】解：过点 M 作 MAOP ，垂足为 A设 PMx，PAx1，MA2则 x2（x1） 2+4，解得 x ，OPPM ，PA 1 ，OP+ PA
14、4，所以点 N 的坐标是（2，4）故选：A15 【解答】解：BC 是A 的内接正十边形的一边由 ABAC， A36，得ABC C 72，又 BD 平分ABC 交 AC 于点 D，ABDCBD ABC36A，ADBD ，BDCABD+A72C ，BCBD，BCBDAD，正确；易证 ABC BCD， ，又 ABAC，故 正确，根据 ADBD BC即 解得 BC AC，故正确，故选：C三、解答题：16 【解答】解： ，由得： x1，由得： x2，不等式组的解集是2x117 【解答】解：（1）设捐 15 元的人数为 5x，则根据题意捐 20 元的人数为 8x5x+8x39， x 3一共调查了 3x+4
15、x+5x+8x+2x66（人） （3 分）捐款数不少于 20 元的概率是 （5 分）（2）由（1）可知，这组数据的众数是 20（元） ，中位数是 15（元） （7 分）（3）全校学生共捐款：（95+1210+1515+24 20+630）66231036750（元） （10 分） 18 【解答】证明：（1）CF 平分BCD，BCFDCF在BFC 和DFC 中，BFCDFC（SAS） （2）连接 BDBFCDFC，BFDF ，FBDFDBDFAB，ABDFDBABDFBDADBC，BDADBCBCDC，DBCBDCBDABDC又BD 是公共边，BADBED（ASA ） ADDE 19 【解答】解
16、：（1）根据题意列表如下：由以上表格可知：有 12 种可能结果，分别为：（1，2） ， （1，3） ， （1，4） ， （2，1） ，（2，3） ， （2，4） ，（3，1） ， （3，2） ， （3，4） ， （4，1） ， （4，2） ， （4，3） ，其积分别为：2，3，4，2，6，8，3，6，12，4，8，12；积为偶数的有 2，4，2，6，8，6，12，4，8，12，共 10 个，则 P（数字之积为偶数） ；（2）所有的可能结果有 12 种，a，b 及 c 的值分别为（1，2，5） ， （1，3，5） ，（1，4，5） ， （2，1，5） ， （2，3，5） ， （2，4，5） ，
17、（3，1，5） ， （3，2，5） ， （3，4，5） ，（4，1，5） ， （4，2，5） ， （4，3，5） ，能构成三角形的有（2，4，5） ， （3，4，5） ， （4，2，5） ， （4，3，5） ，共 4 种，则 P（三线段能围成三角形） 20 【解答】解：（1）（130000100000）50006，能租出 30624（间） （2）设每间商铺的年租金增加 x 万元，则每间的租金是（10+x）万元，5000 元0.5 万元，有 间商铺没有出租，出租的商铺有（30 ）间，出租的商铺需要交（30）1 万元费用，没有出租的需要交 0.5 万元的费用，则（30 ）（10+x）（30 ）1
18、0.52752x211x+50解得：x 15，x 20.55+1015 万元； 0.5+1010.5 万元每间商铺的年租金定为 10.5 万元或 15 万元21 【解答】 （1）证明：连接 ODOAOD ，OAD ODAOAD DAE，ODA DAEDOMNDEMN，ODE DEM90即 ODDE D 在O 上， OD 为 O 的半径，DE 是 O 的切线（2）解：AED90，DE6，AE3， 连接 CDAC 是O 的直径，ADCAED90CADDAE，ACDADE 则 AC15（cm） O 的半径是 7.5cm22 【解答】解：作 ASPQ，CTMN，垂足分别为 S，T由题意知，四边形 AT
19、CS 为矩形，ASCT ，SCAT设这条河的宽度为 x 米在 Rt ADS 中，因为 ， （3 分）在 Rt BCT 中，CBT45，BTCTx （5 分）SD+ DCAB+ BT， ， （8 分）解得 x75，即这条河的宽度为 75 米 （10 分）（其它方法相应给分）23 【解答】解：（1）由函数图象可知，当 0t25 时，函数图象为抛物线的一部分，设解析式为 ya（t25） 2+122.5，把（0，60）代入解析式得，y20.1（t 25） 2+122.5；当 25t40 时，y2122.5；（2）本地广告费用为 x 万元，0x15 时，y 3x +122.5；15x25 时，y 0.1
20、x 2+6x+100；25x40 时，y 0.1x 2+5x+125（3）外地广告费用为 15 万元，本地广告费用 25 万元24 【解答】解：（1）设对称轴 x4 交 x 轴于点 DD（4，0）B（6，0）BD2，由抛物线的对称性得：AD2A（2，0） ；（2）设抛物线的解析式为 ya（x2） （x 6） ，得4a（32） （36）解得a抛物线的解析式为：y x2+ x16（3）四边形 PCQB 为平行四边形PCQB，PCQBP 点的纵坐标为 44 x2+ x16，解得 x3（不符合题意）或 5P（5，4）PC532QB2Q（4，0）或（8，0）P（5，4） ，Q（4，0）或 P（5，4） ，Q （8，0） ；（4）当运行 t 秒时BN2t，AMt，BM4t当BMNBACC（3，4） ，B（6，0） ，由两点间的距离公式得BC5A（2，0）AB4 ，解得 t当BNMBAC 时 ，解得 t
